幕墙立柱连接处的接触力学分析

李绍朗，肖建春，封建波，王泽曦，杜玉涛，吴夏燕

(贵州大学空间结构研究中心，贵州贵阳　550003)

幕墙立柱连接处的接触力学分析

李绍朗，肖建春*，封建波，王泽曦，杜玉涛，吴夏燕

(贵州大学空间结构研究中心，贵州贵阳550003)

为了明确幕墙立柱连接处复杂接触应力分布和可靠连接问题，对立柱—插芯建立有限元模型。建立了多个有限元模型，考虑的参数有风荷载、楼层高度和立柱截面，考虑了材料和接触边界条件的双重非线性，比较了模型及相应双跨连续梁的应力和变形计算结果。分析结果可知，插芯处的应力与双跨连续梁对应位置处的应力有着显著的不同，插芯处的应力呈分段分布，上半部分截面应力呈现双峰值分布，下半部分截面应力处于较低水平，双跨连续梁的应力呈连续上升分布；立柱插芯连接处的形式为半刚性。

立柱—插芯；双跨连续梁；有限元；非线性

立柱是建筑幕墙结构中的主要受力构件之一。幕墙面板上受到的荷载(或作用)首先传给立柱，再由立柱通过锚接点传给建筑物主体结构[1]。因此，立柱的力学性能直接影响到幕墙的安全性和可靠性。在幕墙结构设计与分析过程中，立柱的设计分析通常是幕墙结构设计的一个重要环节，不论是框架式幕墙，还是单元式幕墙，其支撑体系的力学模型都是一致的，根据《玻璃幕墙工程技术规范》JGJ102-2003[2]第6.3.6条规定，幕墙立柱设计分析模型主要分为:简支梁、双跨梁(一次超静定)、多跨铰接静定梁三种力学模型。简支梁力学模型常用于幕墙结构嵌入主体结构中，此时的幕墙计算模型是由主体结构决定的。双跨梁是最为常用的幕墙计算模型，此时幕墙体系悬挂于主体结构之外，每层铝立柱由铝插芯插接串联，该连接点处且可以沿立柱轴向滑动，这样构造方式便形成了连续的规律排布的梁体。上述力学模型，对于立柱计算、设计模型选择问题上，都没有考虑到立柱—插芯之间的连接构造对计算模型的影响，其中简支梁和双跨梁力学模型将该部位视为连续刚接，多跨铰接静定梁力学模型将该部位视为连续铰接，这三类模型无法真实地考虑到立柱—插芯处的受力特点。因此采用非线性有限元方法来研究幕墙关键部位的受力性能是很有必要的。

1　计算模型

1.1模型参数

现代建筑的发展愈发趋于大跨度、大空间结构，诸如火车站、飞机场、购物中心、体育场等建筑物由于其特定的功能需求，其单层跨度也是非常大的(通常单层层高H≥4.2m)。相比于小跨度结构，大跨度结构在同等荷载作用下，变形一般比较大，为了实现立柱的安全可靠，通常采用双跨梁模型进行设计。故本文基于双跨梁模型，考虑插芯与立柱的接触作用来研究幕墙立柱连接处接触问题的力学性能。幕墙立柱水平向承受风荷载和地震作用，竖向承受自重，其中相对于风荷载对模型受力的影响程度而言，自重和地震的影响较小，故本文对立柱的分析只考虑风荷载。

根据《玻璃幕墙工程技术规范》JGJ102-2003 第6.3.3条规定:上下立柱间应留有不小于15mm的缝隙，闭口型材可采用长度不小于250mm的芯柱连接。本文取缝隙间距为20mm，插芯长度为400mm，立柱截断处在离固定支座300mm处，根据文献[3]为了减小支座反力，楼层顶部的两个支座的距离取500mm，计算模型见图2。

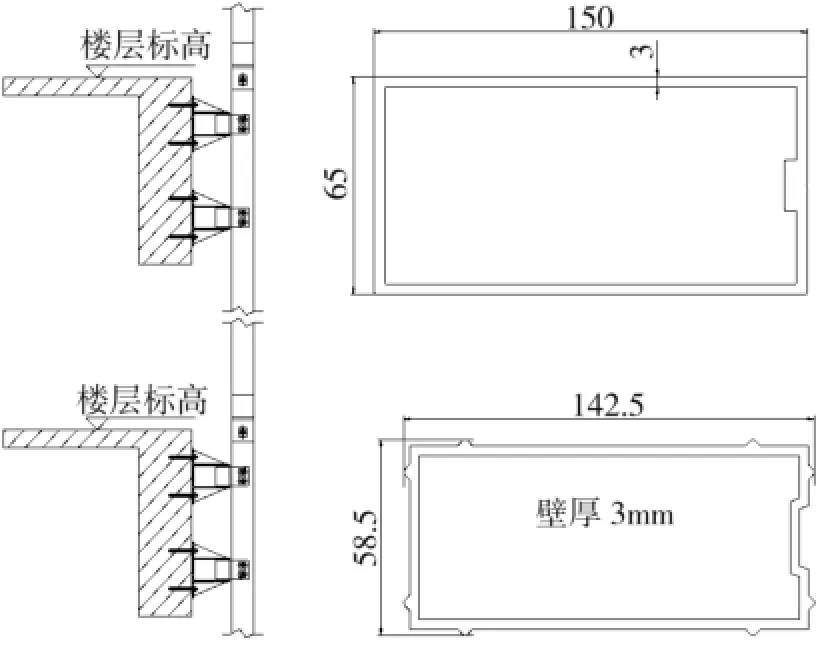
图1　幕墙立柱及150型立柱和插芯截面

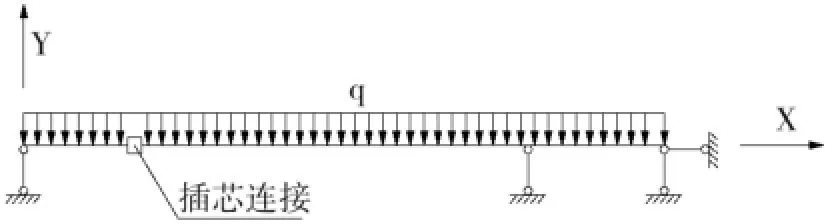
图2　立柱—插芯计算模型

为了研究立柱—插芯接触问题这一节点构造的力学性能，本文采用3个因素，其中风荷载取3个水平，楼层高度和立柱截面取2个水平，共12组模型进行参数化分析。不同模型的参数如表1所示。

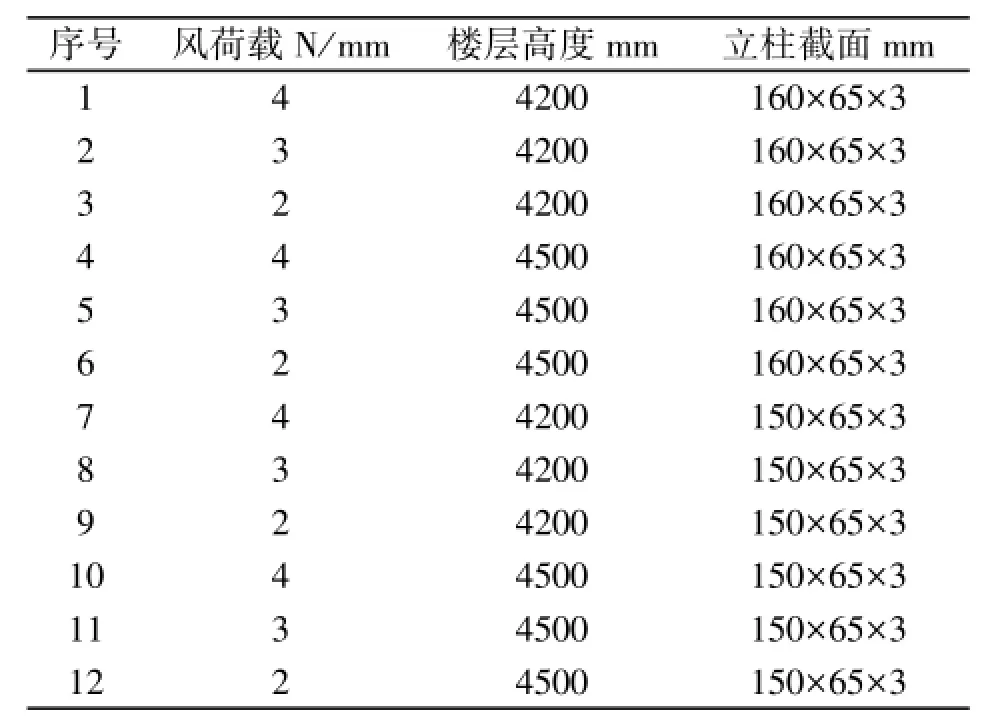
表1　模型参数表

1.2材料参数

立柱和插芯材料均采用6063-T6铝合金，弹性模量E＝70000N/mm2，泊松比v＝0.33，材料摩擦系数u＝0.58，材料需考虑材料非线性，材料的本构关系采用文献[4]中建议的Ramberg-Osgood模型:

采用三段线来定义铝合金的本构关系，6063-T6材料的抗弯、抗压强度设计值为140MPa，f0.2＝180MPa，极限强度为205MPa。材料本构关系图如图3所示:

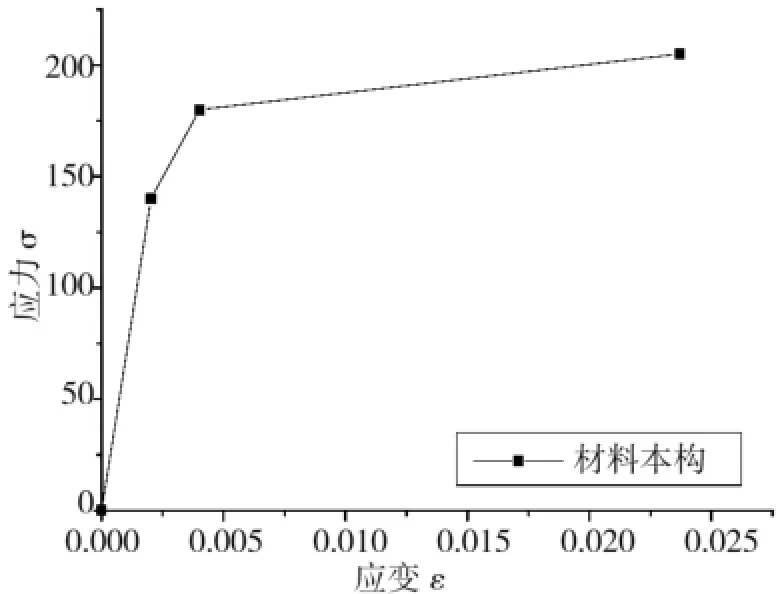
图3　铝合金的应力—应变本构图

1.3有限元模型的建立

研究采用大型有限元软件ABAQUS建立有限元计算模型来分析立柱连接处接触问题的力学性能。采用实体单元建立立柱和插芯，在插芯凸起面与立柱内表面采用通用接触建立了8对面面接触，为了防止插芯滑落，将插芯和立柱通过对穿螺栓连接在一起(见图1)，立柱和插芯的网格单元采用C3D8R线性单元。

2　有限元模型计算结果分析

2.1立柱及插芯应力分析及结果对比

图4　两种模型的应力图比较

这里取模型4作为分析对象，比较模型4和双跨连续梁的立柱应力，从图4(c)中可以看到两种模型的应力分布基本一致，且都小于其屈服强度140MPa，只是在位置为100—500之间应力出现了不同。而这个位置正是立柱与插芯接触的位置，双跨连续梁在该部位应力连续分布，而带有插芯的立柱应力出现分段分布，有些部位还出现了应力集中。为了进一步研究立柱—插芯接触部位的应力分布，将插芯部位的应力单独拿出来分析。

取模型1、4、5、6、10进行对比分析，插芯通过8 个1mm宽的接触面与立柱内部相接触，由于模型具有对称性，不妨取右半部分的4个接触面，从顶部的插芯开始顺时针依次记为接触面1、2、3、4。各接触面的应力分布如图5所示。接触面1的应力主要集中在立柱的截断位置，最大的应力在立柱截断处右端，因为该点在立柱发生变形时，立柱的变形位移较大，而插芯处该点的变形位移小于立柱变形位移，因此发生了严重的挤压，导致插芯接触面部分区域材料屈曲，而在插芯中点，由于没有发生接触，应力比较小，同样在立柱截断处左端也因为挤压造成了应力集中，因而形成了具有双峰值的应力曲线。接触面2有与接触面1相似的应力曲线，但由于接触面2在侧面，主要靠接触摩擦来抵抗立柱—插芯间的滑移变形，同样出现了部分区域的应力集中，但相比于接触面1，其应力幅值要小的多。接触面3、4，由于立柱变形大于插芯的变形，导致下表面和下侧面的接触面分离，除了在插芯接触面两端点与立柱接触外，造成小范围材料屈曲，其余地方的插芯只受插芯变形的弯曲应力，由于插芯比较短，因此这些部位的应力比较小。

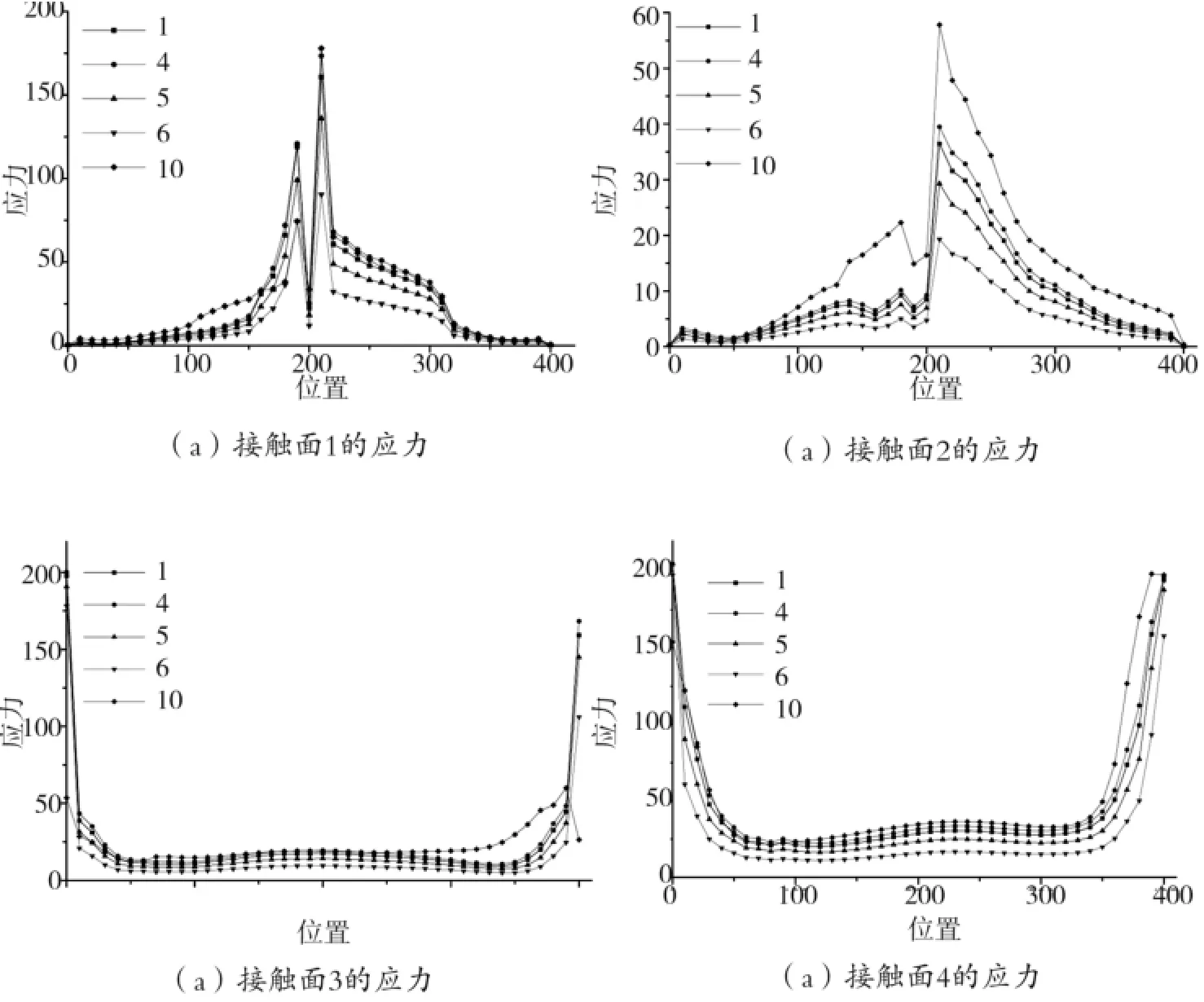
图5　5个模型各接触面上的应力图比较

从图5可以看出在各应力图中，各模型的应力表现出相似的应力曲线，应力的大小排序依次为:模型10、4、1、5、6。比较模型4、5、6可得，在其他条件相同时，风荷载越大，插芯所受的应力越大；比较模型1、4可得，在其他条件相同时，楼层高度较高时，插芯所受的应力越大；比较模型4、10可得，在其他条件相同时，立柱截面尺寸越大，插芯所受的应力越小。模型1、4、10的应力大小可归结为刚度原因，同条件下，模型10的截面小于模型4，其刚度要小于模型4；模型1的跨度比模型4小，其刚度要大于模型4，因此形成了图5所示的应力图。

2.2立柱位移分析及结果对比

经有限元计算得到12组模型的跨中最大位移，并与对应的双跨连续梁、简支梁、双跨铰接梁的跨中最大位移一起列在表2中，位移单位为mm。

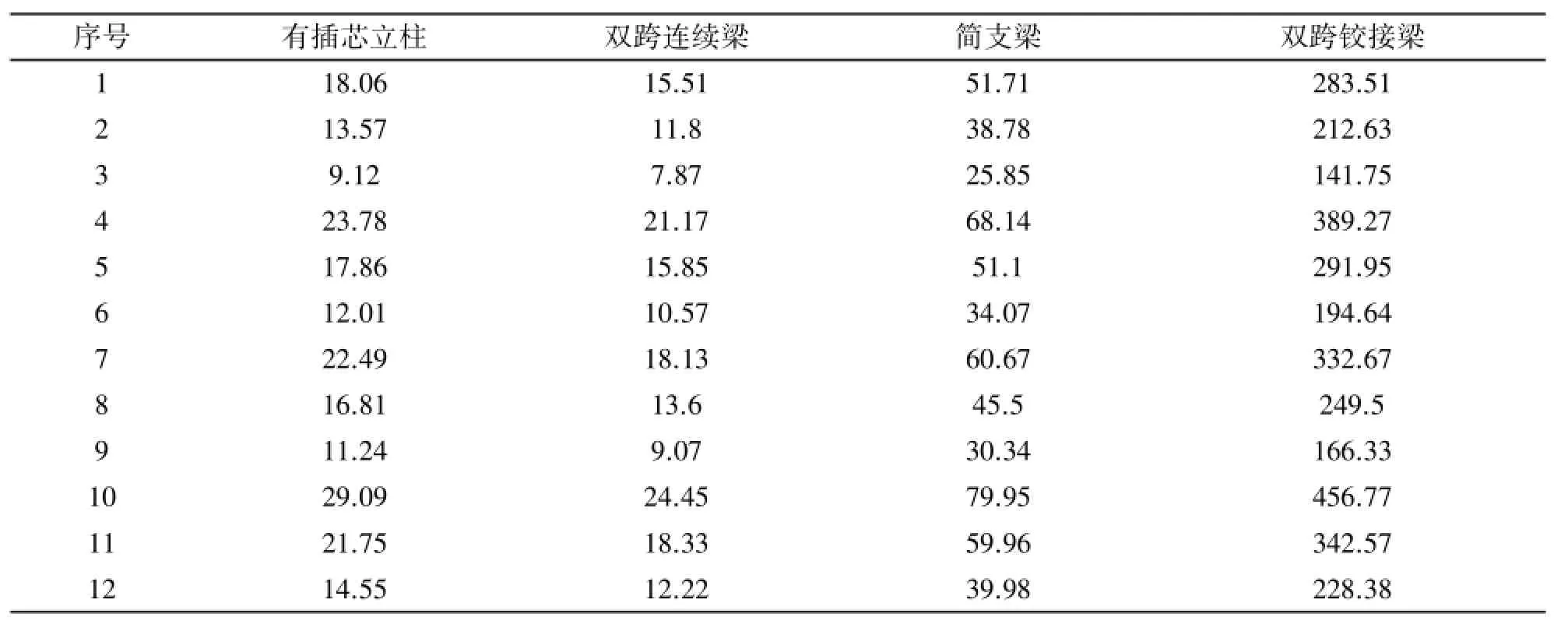
表2　各种模型跨中最大位移值对比

不同力学模型最大位移对比:从表2中可以看出在单层跨度比较大的时候，采用双跨连续梁得到的跨中最大位移要比简支梁小很多，采用本文所选的参数，双跨连续梁跨中最大位移约为简支梁的0. 3，对于 4200层高的双跨连续梁的容许挠度为3700/180＝20.56，简支梁为4200/180＝23.33，比较表中位移，得到双跨连续梁的位移均满足要求，而简支梁均不满足，若采用简支梁模型计算则设计出来的立柱截面会很大，造成材料浪费，因此，采用双跨连续梁为基础模拟大层高的幕墙立柱是合理的。表中可以得出，有插芯立柱的跨中最大位移介于双跨连续梁和双跨铰接梁之间，因此，可以得出立柱—插芯接触处的刚度介于刚性和铰接之间，属于半刚性。

从图6可以看出有插芯立柱和双跨连续梁的位移在各个位置上的差值不是很大，并结合表2来看，有插芯立柱的跨中位移比简支梁要小的多，因此，在实际设计时，对于层高较大的结构，采用双跨连续梁模型比较合理。就拿模型4来说，其跨中最大位移为23.78>4000/180＝22.22，对应的双跨连续梁为21.17<22.22，有插芯立柱的模型其挠度不满足要求，双跨连续梁满足要求，但实际设计中风荷载往往会乘以一个1.4的放大系数，因此，采用双跨连续梁模型基本满足实际的要求，并且其安全性也不会有太大的降低。

比较模型1、4、5、6、10的跨中位移，从图7中可以看到，各模型的位移曲线相似。模型1、4其他条件相同，而跨度不同，模型1跨中最大挠度18.06 <20.56，而模型4跨中最大挠度23.78>22.22，可知，跨度越大，其模型受力越不利。等跨连续梁跨中最大位移为，最大位移与荷载成正比，有插芯立柱的模型与其有着相似的跨中最大位移，模型4、5、6，由于立柱材料基本处于弹性变形状态内，因此其跨中最大位移正比于所施加的风荷载。模型4、10其他条件相同，而立柱截面不同，模型10的位移大于模型4，模型10的最大位移已超过容许挠度，模型10强度不够，因此在设计时建议加大截面尺寸。

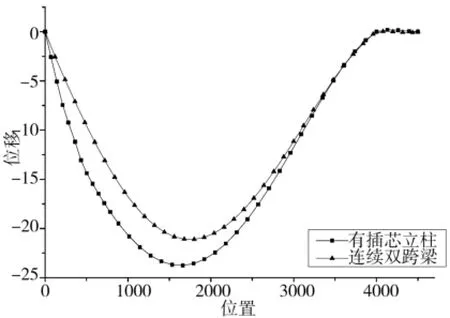
图6　模型4与双跨连续梁的位移图

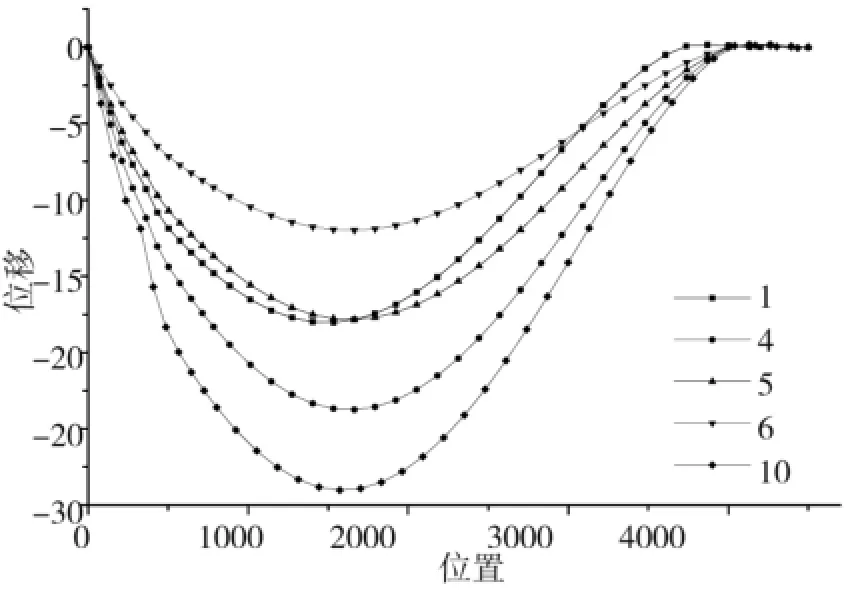
图7　5个模型跨中位移图

3　结论

(1)从应力的角度分析，带插芯的立柱模型与双跨连续梁的应力在插芯接触部位存在着显著的差别，双跨连续梁模型应力连续分布，带插芯的立柱模型出现应力集中，主要是由于立柱—插芯的接触边界条件非线性引起的应力变化。插芯处应力在截面上半部分，由于受挤压所造成的接触使得应力出现具有两个峰值的不连续分布；截面下半部分，由于接触面分离造成插芯只受弯曲应力，使得应力处在一个比较低的水平。

(2)从变形的角度分析，带插芯的立柱模型与连续梁模型的跨中位移非常接近且变形曲线相似，并且远小于双跨铰接梁，立柱—插芯连接处属于半刚性，或者可以说是极其接近刚性的半刚性。

[1]龙国才.如何用有限元对幕墙立柱进行力学计算[D].2001年全国铝合金门窗幕墙行业年会论文集锦.2001.3.

[2]JGJ133-2001《玻璃幕墙工程技术规范》[S].

[3]陈光华，刘万奇.幕墙立柱双跨梁力学计算模型的探讨[J].铝门窗幕墙，2006(9):15-20.

[4]郭小农，沈祖炎，李元齐，等.国产结构用铝合金材料本构关系及物理力学性能研究[J].建筑结构学报，2007，28(06):110-117.

(责任编辑:王先桃)

Contact Mechanics Analysis of Curtain Wall Column Joints

LI Shaolang，XIAO Jianchun*，FENG Jianbo，WANG Zexi，DU Yutao，WU Xiayan
(Space Structure Research Center，Guizhou University，Guiyang 550003，China)

In order to make clear the complex contact stress distribution and the reliable connection of the curtain wall column joints，the finite element model of the column and plug was established.Several finite element models were established，and the parameters of the model are wind load，height of the floor and the cross section of the column，the double nonlinearity of material and contact boundary conditions were considered，the calculation results of stress and deformation of the model and its corresponding double span continuous beam were compared. The results show that the stress at the plug and the stress at the corresponding position of the double span continuous beam are significantly different，the stress of the plug is segmented，the stress at upper part of the section is double peaks distribution，and the stress at lower part of the section is in a low level，the stress of double span continuous beam is continuously increased；the form of the column-plug connection is a semi rigidity.

column-plug；double span continuous beam；finite element；nonlinear

TU395

A

1000-5269(2016)01-0117-05DOI:10.15958/j.cnki.gdxbzrb.2016.01.27

2016-01-15

贵州省教育厅项目[黔教合KY字(2012)045号]

李绍朗(1992-)，男，在读硕士，研究方向:大跨度空间结构，Email:2857443989＠qq.com.

肖建春，Email:jcxiaogzu＠163.com.