基于卷积的安全双方计算问题

唐瑜穗，许道云

(1.贵州大学理学院，贵州贵阳　550025；2.贵州大学计算机科学与技术学院，贵州贵阳　550025)

基于卷积的安全双方计算问题

唐瑜穗1，许道云2*

(1.贵州大学理学院，贵州贵阳550025；2.贵州大学计算机科学与技术学院，贵州贵阳550025)

经典的安全双方问题一直专注于零信息泄露的模式，虽然这是理想的安全双方模型，但在实际的安全双方计算中需要付出昂贵的代价且效率不高。本文在传统安全双方的问题上构建卷积安全双方问题，并基于此问题建立不公开信息和需要部分信息公开的安全双方计算模型，提供一种兼顾安全和效率的方法。

安全双方问题；卷积安全双方问题；信息公开

最早的安全双方问题[1]源于图灵奖得主姚期智(Andrew Chi-Chih Yao，1982)1982年提出的百万富翁问题:两个富翁想比较他们的财产，但都不希望对方知道自己的财产数量。该问题的本质即是在保护隐私的前提下比较这两个富翁财产数量的大小。5年后Goldreich，Micali和Wigdersn提出了可以计算任意函数的安全双方协议[2]，并将安全双方问题推广到安全多方问题。后来Lindell和Pinkas提出保护隐私的数据挖掘并把安全双方计算首次运用于分布式数据挖掘中[3]。2004年Malkhi用cut-and-choose[4]方法第一次证明在一个恶意模型下实用的方案。随着马敏耀代理安全多方计算协议[5]的提出，代理签名的概念移植到安全多方计算中弥补了安全双方计算在实际应用中面对在需要执行某个协议时部分参与者可能会因为某些原因而无法即时地执行协议的缺陷。

有关安全双方计算的研究主要集中在以下几个方面:对一般意义的安全双方计算协议的研究[6]，研究的目的是设计一种高效安全的、能够计算任意函数的安全双方计算协议；对一般化的安全双方计算协议进行取舍[7-9]，通过舍去对具体应用没有意义的部分来提高效率；对安全双方计算的定义的研究，因为安全双方计算至今还缺乏一个为大家所认同的完备的定义；构造新的安全双方和多方计算协议[10-13]和多方计算协议生成器方面的研究。

已有的安全双方计算协议都有一个共同的安全前提，即假定数据存储在参与者自己或者安全可靠的设备中。但随着计算机网络技术和应用的飞速发展，计算的含义及方式发生了巨大的改变。电子商务等互联网应用推动的云计算和共享存储平台[14]也使参与者的数据不再局限于参与者自身认为安全可靠的设备中。例如，当利用网络进行商业活动时，常常需要建立某些网络协议来要求参与者提供自己的数据。如果此时存在一个可信第三方，参与者只需要将自己的输入保密地传送给它，由它计算这个函数，然后将计算结果保密发送给每个参与者即可。但是在现实世界中，很难找到一个各方都信任的第三方。

在这种公开的环境下，传统的安全双方计算协议的前提不再存在，甚至参与者还会要求公开一部分信息，来预判参与者的诚意，又或者参与者存在恶意攻击的可能。正是对于没有绝对意义上可信的第三方的这种公开的环境，本文主要考虑引入一种特殊的第三方，并通过对卷积问题的信息保密模型和安全性兼顾效率模型的建立，来讨论在安全双方计算中同时兼顾两者的可行性和必要性。通过对卷积隐藏技术下适用于不同背景的安全双方协议的构造，找到更适用于现实世界的安全双方模型。

1　基础知识

参与者(players):安全双方计算中的决策主体，通过与其他参与者和第三方合作来达到预期目的。我们一般用Alice和Rob表示两方安全计算的两个参与者。文中我们简称A和B。在实际情况中，由于各方面的原因，参与者并不一定会遵守协议，可能会根据自己在协议过程中得到的中间信息去推导另外参与者的隐私。可以把他们分类为诚实参与者、半诚实的参与者和恶意的参与者。

诚实的参与者在协议的执行过程中行为都是诚实的，他们能够完全按照协议的过程正确完整的执行协议所规定的每一步步骤，同时在执行过程中会保密自己的输入和中间结果。半诚实的参与者在协议执行方面会完全按照协议所规定的每一步步骤执行，但他可能会将自己的输入输出或者中间结果等信息泄漏。恶意的参与者不一定会完全按照协议的步骤去一步一步的正确执行协议，同时也可能对协议本身进行破坏和攻击，会将自己的输入或者中间结果泄露给其他人，甚至直接中断协议。而安全多方计算中需要保护的是诚实参与者的各种安全需求。

私人信息(private input):在安全双方计算中，每个参与者拥有的输入，我们常用函数或者序列来表示，文中用x(n)和y(n)表示两个参与者的私人信息。

安全双方计算(secure two-party computation):在一个互相不信任(不愿泄露信息)的分布式网络中，两个参与者A和B在合作计算得到某函数p(x1，x2)的结果。这里的输入x1和x2分别来自两个参与者的私人信息。计算结果使每个参与者都能根据协议得到自己预期的输出但不知道其他参与者的信息，也不能根据中间信息推导其他参与者的信息。

第三方(Intermediary):帮助参与者完成安全计算且不会向每个参与者泄露其他参与者的信息的实体。第三方必须严格的按照协议的要求执行协议，不能通过记录协议的中间数据来推断其他参与方的私有输入，也不能和其他参与者进行串通。通常只在协议开始的预处理阶段参与执行，不参与协议的运算过程，也不具有运算能力。常用于处理一些不能被参与者得知的信息分配，不属于参与者，所以从理论上来说也不能获得运算结果。

安全双方计算模型:安全双方计算模型分为诚实模型、半诚实模型和恶意模型。

诚实模型是指计算模型中所有的参与者都是诚实参与者的安全双方计算模型，参与者满足一切诚实行为，不会在协议执行的过程中泄露中间信息与结果。半诚实模型是指计算模型中所有的参与者都是诚实或者半诚实的安全双方计算模型，参与者按照协议的规定执行，但同时参与者也有泄露信息的可能。本文的模型正是基于半诚实的计算模型。恶意模型是指有参与者或攻击者是恶意的参与者的安全双方计算模型，并不一定所有参与者都是恶意的参与者。

安全双方协议(protocol):安全双方协议是各个参与者在整个计算过程中必须遵守和执行的标准，是为了参与者能安全的进行双方计算而建立的规则和标准。

结果(Result):安全双方计算的目的，安全双方的计算输出函数p(x1，x2)。

2　卷积安全双方问题

通过对卷积问题的信息保密模型和安全性兼顾花费模型的构造，讨论了在安全双方计算中兼顾两者的可行性和必要性。文中采用的是序列卷积的定义，对于每个参与者我们认为其带了一个隐私序列。

在泛函分析中，卷积是通过两个函数和生成第三个函数的一种数学算子，表征函数与经过翻转和平移的重叠部分的面积。如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“滑动平均”的推广。对于参与者Alice和Rob，参与者的信息以函数或者序列的形式保存。

对于以函数形式保存信息的参与者，f(x)和g(x)分别为Alice和Rob的私有信息，同时也是实数域上的两个可积函数。f(x)和g(x)的卷积用表示。

记为:(f*g)(x)＝h(x)

对于以序列形式保存信息的参与者，若两个序列x(n)和h(n)分别为Alice和Rob的私有信息，则他们的卷积y(n)为，记为:x(n)*h(n)＝y(n)，两个序列的卷积是两个变量在某范围内相乘后求和的结果。

卷积函数具有以下性质:

分配律:

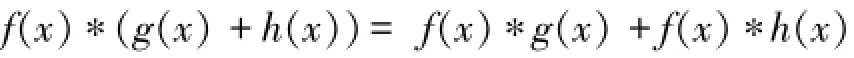
结合律:

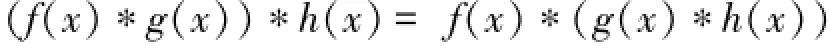
交换律:

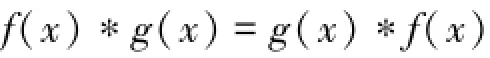
本文的主要工作是在序列卷积定义的基础上研究卷积问题。从而提出了两类模型:一是不公开信息的卷积问题模型；二是需要公开信息的卷积问题模型。

卷积安全双方问题:参与者A和B分别拥有参与者的私人信息x(n)和y(n)，其中x(n)＝(x1，x2，…，xn)，y(n)＝(y1，y2，…，yn)。第三方随机产生一个只有参与者B知道的序列v＝(v1，v2，…，vn)，协议结束使参与者A得到结果u。其中

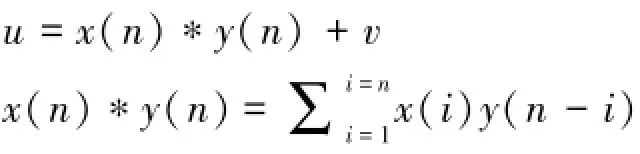
问题的输入:x(n)和y(n)和v(n)

问题的输出:函数u

3　计算模型

我们考虑两类计算模型，一类模型是安全双方计算过程中保证信息完全安全，不被泄露。另一类模型需要公开部分信息或允许部分信息被其他参与者知道。首先我们讨论保证参与者信息安全的模型。

3.1不公开信息的卷积问题模型

建立不公开信息的安全双方计算模型，即理想的安全双方模型，过程中不允许信息泄露。在这个前提下我们引入一个第三方(最早的商用服务器[15]是由D.Breaver在2001年提出，也就是现在第三方的前身)，这个特殊的第三方参与安全双方的计算，却不能推导隐私数据也不能和参与者进行串通。它只是辅助安全双方的计算，比如产生一个随机数据，或者在开始的时候参与密码的分配，它不能得到结果也不能以参与者的数据作为依据产生数据，也就是说参与者的信息不会泄露给第三方。这样的第三方比需要参与者提供私有信息的第三方安全，同时在现实生活中，要求绝对安全的第三方是很难实现的，但我们所提到的这样的第三方却是可以实现的。通过这个第三方参与卷积问题的计算协议1。

3.1.1协议1

输入:参与者A的信息x(n)＝(x1，x2，…，xn)，

参与者B的私有信息y(n)＝(y1，y2，…，yn)。

输出:协议结束后，参与者A可以知道结果

x(n)*y(n)+v(n)，其中v(n)只有参与者B知道，协议结果不泄露v(n)给A。

在这个过程中分为4步:

(1)第三方产生一对随机向量qa和qb，令ra+ rb＝qa*qb，可以得到另外一对随机向量ra和rb，然后这个第三方把qa和ra发送给参与者A，把qb和rb发送给参与者B。

(2)A把自身序列和ra的组合x1＝x+qa发给B，B把y1＝y+qb发给A。

(3)B收到A发来的信息后，随机产生一个序列v1，计算出结果x1*y+v1再把这个结果发送给A。同时根据产生的v1，计算出v＝v1-rb。

(4)A收到B发来的信息后，计算出

每个参与者的动作如表1所示:

表1　不公开信息的参与者动作

通过每个参与者的动作画出流程图如图1所示。

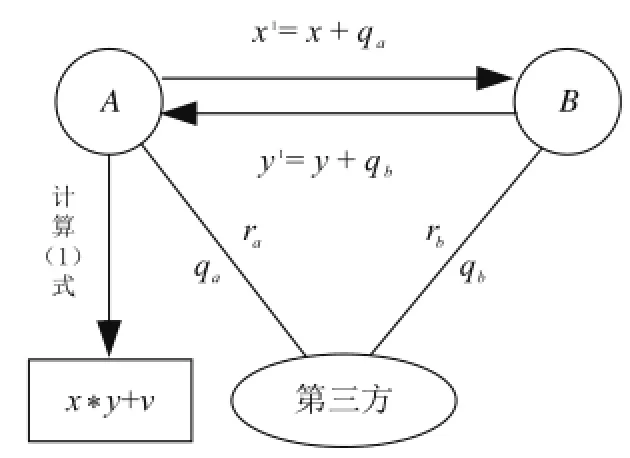
图1　参与者流程图

3.1.2协议可行性分析

考虑协议的可行性我们需要证明在协议过程中参与者A无法知道B的信息，同时B也无法知道A的信息。即A不能在协议过程中知道y(n)或者说通过推导得到y(n)。同理参与者B也不能在协议过程中知道x(n)或者推导出x(n)。

一方面要证明A无法知道信息y(n)，首先假设A知道另一参与者的信息y(n)。也就是说协议不安全，即存在一个算法使得对于任意参与者B使得协议结果得到B的隐私数据y(n)，由表1可知协议运算过程中:

(1)A知道x1，其中x1＝x+qa

(2)A知道y1，其中y1＝y+qb

(3)A知道x1*y+v1，记φ＝x1*y+v1

最后A得到x*y+v，即对于给定的x1和任意的y，如果x1，y1，φ满足上面(1)(2)(3)，则对于协议输入x1，y1和φ，可得到输出:y(n)。

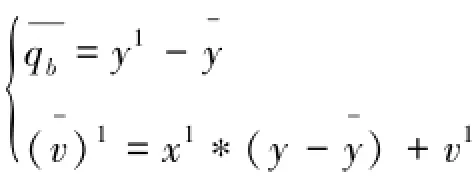
根据协议1的计算过程，可知协议过程中产生

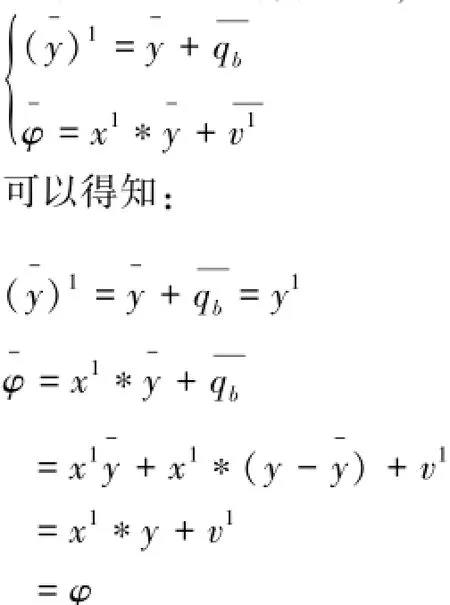
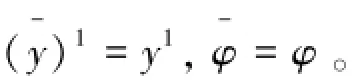
即可见输入依然为x1，y1和φ，所以输出依然为y(n)而不是y(n)，所以与存在一个算法使得对于任意参与者B使得协议结果得到B的隐私数据导出矛盾。因此我们的假设不成立，参与者A不能探知到信息y(n)，也就是说在协议的过程中参与者A不能得知参与者B的信息。

另一方面B也无法知道x(n)，如表1所示，在计算过程中始终把x(n)加上一个由第三方随机产生的序列qa发送给B，同时B除了知道x1不知道任何与A有关的信息。所以在这个协议过程中保证了B无法知道A的信息x(n)，也就是说B无法窥探参与者A的隐私。

由此我们可以得到卷积安全双方问题的解决方案是可行的也是保证安全的。

3.2需要公开信息的卷积问题模型

传统的安全双方计算要求各自的信息不公开给对方，但在实际的操作中，要达到信息零泄露是很大的工程，花费较大，效率也较低。同时在现实生活中，也存在需要公开一部分信息的安全双方问题，比如两个百货公司要比较营业额，双方要求公开一部分商品售出的单价或进价来达成合作，而不是如传统安全双方问题一样不公开任何信息。对此我们考虑对于参与者都能接受的安全程度的双方模型，这样既降低了花费同时也提高了效率。下面我们考虑一种需要公开一部分信息的卷积问题模型。

在这个问题中参与者要求信息可以泄露一部分，我们定义x含有n个元素，且n是偶数。我们把x分为xa和xb，分别含有x的n/2个元素。同理，也可以定义出类似的ya和yb。

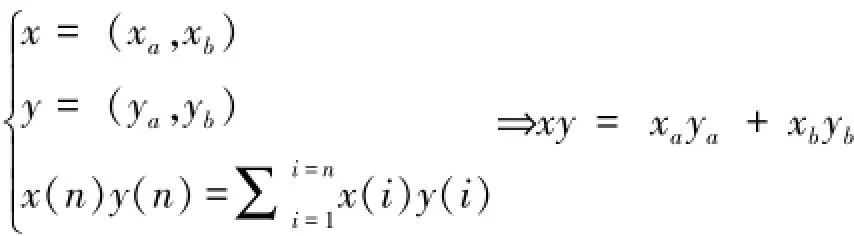
通过以下两步来计算u＝x*y+v:

(1)A发送xb给B，同时B发送ya给A。

(2)A计算出u＝xa·ya，B计算出v＝-xb·yb。

通过这两步构造协议2。

3.2.1协议2

输入:参与者A的数据x，参与者B的数据y。

输出:A得到u＝x*y+v，其中v只有参与者B知道，v不泄露给A。

计算过程如下:

(1)A和B合作产生一个随机序列z(n)＝(z1，z2，…，zn)。令矩阵

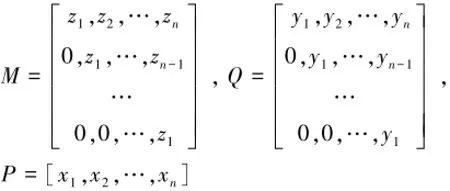
(2)A计算x1

A把x1划分为两个部分，分别为，并且把发送给参与者B。

(3)B计算出y1＝M-1Q后，同样把y1划分为两个部分并把发送给参与者A。

(4)A收到B发来的信息后，计算

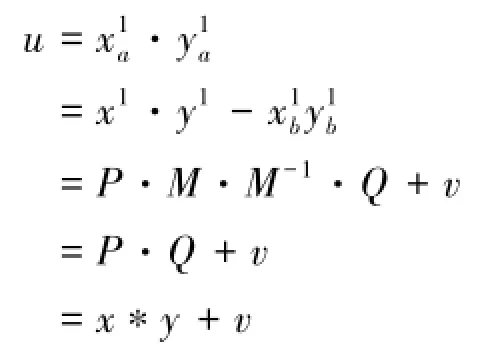
为了更直观的分析协议过程，每个参与者的动作见表2:

表2　公开部分信息模型的参与者动作

参与者的流程图如图2所示。

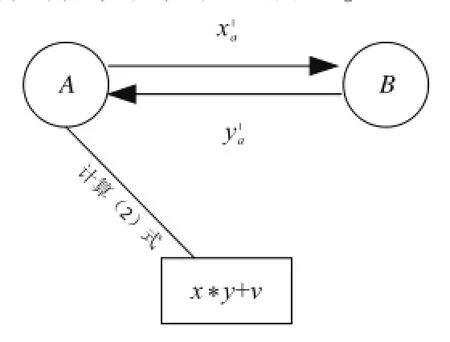
图2　参与者流程图

3.2.2协议可行性分析

讨论这个协议是否安全，需要知道A和B互相知道对方的多少信息，能否从协议的计算过程中推导出双方的原始数据。即需要证明在协议过程中参与者A无法知道B的信息，同时B也无法知道A的信息。也就是说A不能在协议过程中知道y(n)或者说通过推导得到y(n)。同理参与者B也不能在协议过程中知道x(n)或者推导出x(n)。

一方面要证明A无法知道信息y(n)，首先假设A知道另一参与者的信息y(n)，也就是说协议不安全。即存在一个算法使得对于任意参与者B使得协议结果得到B的隐私数据y(n)，由表2可知协议运算过程中:

(1)A知道x1，其中x1＝x*z。

最后A得到x*y+v，即对于给定的x1和任意的y，如果x1，y1满足上面(1)(2)，输入x1，y1，可得到输出y(n)。

另一方面，通过这个协议B也无法得知A的信息，因为协议运算过程中将x1的结果分成两部分，其中一部分发给B，B从x1＝x*z中知道x的n/2个数据。而x(n)＝(x1，x2，...，xn)是一个n元的未知变量，同时x1＝x*z是关于n个未知变量的线性方程组。如果B知道所有的n个方程式，B能通过解线性方程组得到x，但B仅仅知道n/2个方程。而在理论上，通过解实数域上n/2个方程求n个未知变量有无穷解。因此，尽管B知道A的一半数据，但这要使得B知道A的全部信息是远远不够的。

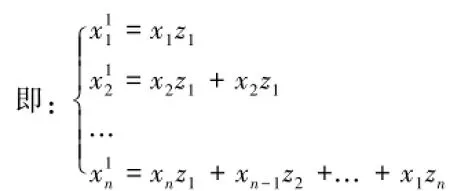
由此可以得知协议2是可行的也是保证安全的。

4　结语

本文在传统安全双方问题上构建了卷积安全双方问题，并基于此问题建立了不公开信息和需要部分信息公开的安全双方计算模型。允许泄露部分信息的安全双方计算模型比传统的零信息泄露模型具有更多的实际意义，更能实现参与者的具体要求。

因为对于现实世界，参与者的需求并不只在于我们所认知的范围，权衡安全和效率这样的模型能更好地满足参与者的实际需求，我们可以通过参与者对信息安全重要性的评估来制定相应的安全双方模型。但在这里需要提的是泄露信息的意思并不是无条件的泄露，也不是类似恶意参与者的泄露中间结果及信息。这里的“泄露”可以说是公开，是在协议开始前双方公开一部分自己的私有输入，但在协议过程中严格执行协议，不泄露信息给其他参与者。

可见我们提出的卷积问题具有现实意义；通过降低安全双方问题的安全性在参与者可以接受的范围内来提高效率是可行的，也是有实际意义的。

[1]Yao A C.Protocols for secure computations[C]//Symposium on Foundations of Computer Science，Proceedings of the 23rd Annual IEEE Symposium on Foundations of Computer Science，Berkeley，California: Symposium on Foundations of Computer Science，1982:160-164.

[2]Goldreich O，Micali S，Wigderson A.How to play any mental game [J].In Proc of 19th STOC，1987，22(11):11-13.

[3]Lindell Y，Pinkas B.Privacy preserving data mining[J].Springer Berlin Heidelberg，2000，1880(3):36-54.

[4]Malkhi D，Nisan N，Pinksa B.Fairplay A secure two party computation system[J].In Usenix Security Symposium，2004，13(4): 287-302.

[5]Minyao M.Research on secure multi-party computation and its extended problems[M].Beijing:Beijing university of Posts and Telecommunications Press，2010:109-117.

[6]Atallah M J，Du W.Secure multi-party computational geometry [J].International Workshop on Algorithms&Data Structures，2004，2125:165-179.

[7]Pinkas B.Cryptographic techniques for privacy preserving data mining[J].Acm Sigkdd Explorations Newsletter，2002，4(2):12-19.

[8]Lindell Y，Pinkas B.Secure multiparty computation for privacy pres -erving data mining[J].Journal of the ACM，2009，1(1):59-98.

[9]Salman N，Babak S，Payman M，Seyed S S.A Privacy-Preserving intrusion detection system using secure Two-Party computation protocols[J].Comput.J，2014，57(4):494-509.

[10]Dankar F，Brien R，Adams C，et al.Secure multi-party linear regression[C].Ottawa:EDBT/ICDT Workshops，2014:406-414.

[11]Karr A F，Lin X，Sanil A P，Reiter J P.Secure regression on distributed database[J].J Computational&Graphical Statist，2005，14(2):263-279.

[12]Du W，Han Y S，Chen S.Privacy-preserving multivariate statistica analysis:Linearregressionandclassification[J].Siam International Conference on Data Mining，2004，233:222-233.

[13]Hall R，Fienberg S E，Nardi Y.Secure multiple linear regression based onhomomorphicencryption[J].JournalofOfficial Statistics，2001，27(4):669-691.

[14]Beaver D.Commodity-based cryptography(extended abstract) [C].Stoc Proceedings of the Twenty Ninth Annual Acm Symposium on Theory of Computing，EI Paso:Acm Symposium on Theory of Computing，1997:446-455.

[15]Dean J，Ghemawat S.MapReduce:A flexible data processing tool [J].Communications of the ACM，2010，53(1):72-77.

(责任编辑:周晓南)

A Secure Two-party Computation Problem Based on the Convolution

TANG Yusui1，XU Daoyun2*
(1.College of Science，Guizhou University，Guiyang 550025，China；2.College of Computer Science& Technology，Guizhou University，Guiyang 550025，China)

The classic security two-party computation problem has focused on the mode of zero information leakage.Although it is the ideal model for the security computation，it is costly and inefficient in the actual calculations.The convolution security two-party computation problem was proposed from the traditional model.A secure of no-information-disclosed calculation model and a secure issue of some information disclosure were established based on the convolution two-party computation problem，which provided a method for balance between safety and efficiency in the security two-party computation problem.

security two-party computation problem；convolution security two-party computation problem；information disclosure.

TP309.2

A

1000-5269(2016)01-0052-06DOI:10.15958/j.cnki.gdxbzrb.2016.01.13

2015-11-20

国家自然科学基金项目资助(61262006)

唐瑜穗(1990-)，女，在读硕士，研究方向:计算复杂性，Email:tys.618＠163.com.

许道云，Email:dyxu＠gzu.edu.cn.