基于条件粒子滤波的高动态高灵敏度GNSS信号跟踪算法
2016-10-29徐昊玮廉保旺唐成凯何伟
徐昊玮,廉保旺,唐成凯,何伟
(西北工业大学电子信息学院,陕西西安 710072)
基于条件粒子滤波的高动态高灵敏度GNSS信号跟踪算法
徐昊玮,廉保旺,唐成凯,何伟
(西北工业大学电子信息学院,陕西西安 710072)
随着北斗全球定位卫星系统的逐步完善和GPS等卫星系统的更新换代,卫星接收机的灵敏度需求也逐渐提高,而导航信号的微弱性和卫星与接收机之间的相对运动导致现有的卫星接收机高灵敏度跟踪算法的精度无法满足需求。针对这种情况,提出了一种基于粒子滤波的高灵敏度高动态跟踪算法。该算法利用粒子滤波对跟踪环路的各个因子进行修正,并在信号强度和动态应力自适应辅助调节下,实现高精度的接收机高灵敏度跟踪。该算法可以有效降低加加速度对跟踪环路的影响,对突发动态性改变具有较好的跟踪性能。将文中所提出的方法与现有的多种跟踪算法从估计准确度、动态性能和载噪比影响三方面进行分析对比,结果表明新算法相比于现有的跟踪算法能有效提高了接收机的估计准确度和动态性能,并降低载噪比的影响。
高动态;高灵敏度;粒子滤波;跟踪
目前,全球卫星导航系统(GNSS)已经成功在全世界范围内为用户提供了精准的位置、速度信息和时间信息。然而,在传统的接收机中,跟踪环路的参数是预先设置并保持不变的[1]。该类方法将跟踪环路的带宽设定为固定值,算法结构简单,易于实现,但固定的环路参数使得跟踪环路在一部分时刻的工作状态处于次佳,导致传统的跟踪环路不能满足动态性要求较高的应用环境。
为了满足当前卫星接收机对跟踪环路灵敏度的需求,文献[2-3]分别提出了基于Viterbi和基于卡尔曼滤波的高灵敏度跟踪算法,这2种算法通过对相关值或鉴相误差进行处理来实现高灵敏度的跟踪。但这2种算法相对较为复杂,信息处理延迟较大,所以很难满足高速载体的跟踪需求。文献[4-5]提出了利用惯性导航技术来解决高动态跟踪,但由于惯性器件价格昂贵,现有的大部分接收机载体并没有安装这类辅助传感器来获得接收机自身的运动参数信息,而且当导航信号突然恶化时,整个导航系统会因为惯导器件突然恶化的对准误差而发散。文献[6-7]中提出了一种当前值预测的变带宽锁相环(current value,CV)的跟踪环路算法,该算法利用每次观测出的载噪比和动态性计算跟踪环路的最优带宽,对动态性的变化灵敏度较高。但该算法没有对噪声进行抑制,导致跟踪环路抖动较大。文献[8]提出了一种基于卡尔曼滤波变带宽锁相环(Kalman filter,KF)的跟踪环路算法,该算法对每次观测出的载噪比和动态性进行卡尔曼滤波,并根据滤波值计算环路的最优带宽,对噪声的抑制性较高,但对加加速度突变跟踪灵敏度较低。文献[9]提出基于SIR粒子滤波的跟踪环路算法,该算法可以获得较高的跟踪灵敏度,但该算法无法跟踪加加速度,所以对突变速度的跟踪灵敏度较低。
针对上述问题,本文提出了一种基于粒子滤波的高灵敏度高动态跟踪算法,该算法将信噪比和动态应力的双参数引入自适应最优带宽,利用粒子滤波对三阶环路进行动态估计得到高灵敏度的跟踪环路参数[10]。粒子滤波是一个基于样本空间的预测算法,它没有状态方程仅根据当前值与预测值的误差调整下一步预测值,并且当缩小样本空间大小后,粒子滤波方法对于突然产生的加加速度有很好的估计效果并对噪声的抑制效果也较为可观。仿真结果表明本文所提出的跟踪算法与传统的固定带宽和参数的跟踪算法相比较可以更加快速地根据接收机当前的动态性能调整参数,并且在高速载体的情况下也能保持环路跟踪的稳定性。
1 跟踪算法模型
在高动态条件下,载体相对于卫星的运动状态处于一种快速的变化状态[11]。在没有任何惯性器件辅助的情况下,为了保证GNSS接收机的跟踪环路处于最优的工作状态,GNSS接收机需要实时对跟踪环路参数进行调整以保证高动态条件下载波跟踪环路的跟踪精度。由文献[6]可知,GNSS接收机跟踪环路的最优带宽与信号的载噪比以及载体相对于卫星的运动状态有关。因此要得到最优化的环路带宽首先需要对载体相对于卫星的运动状态参数进行估计[12]。但是在高动态条件下运动状态参数的变化较快且运动状态参数变化较为复杂。为了在高动态条件下对运动状态参数进行准确估计和预判,本文设计了基于条件判决的SIR粒子滤波器(CSIR)用于对接收机的信号质量和动态性进行估计,同时结合相应的最优化环路带宽计算公式得到最优化的环路带宽以保证GNSS接收机在高动态条件下的环路跟踪精度,并提高了接收机的环路的跟踪灵敏度。
1.1跟踪环路带宽
当跟踪环路处于最优的跟踪带宽时,环路能在当前的信号条件下输出的鉴相误差值最小[13],从而实现对信号的最优跟踪,根据文献[6]可知,载波环与码环的最优带宽分别为(BL)PLL-optimum和(BL)DLL-optimum,且都主要由载噪比C/N0、动态应力和积分时间所决定;此外,码环最优带宽还与前后相关器距离有关,如下:
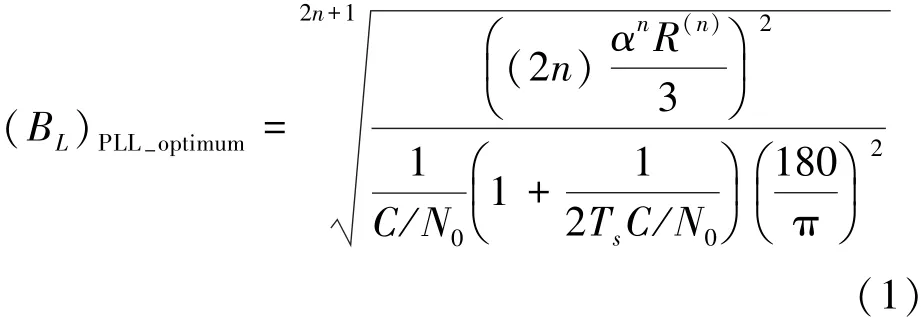
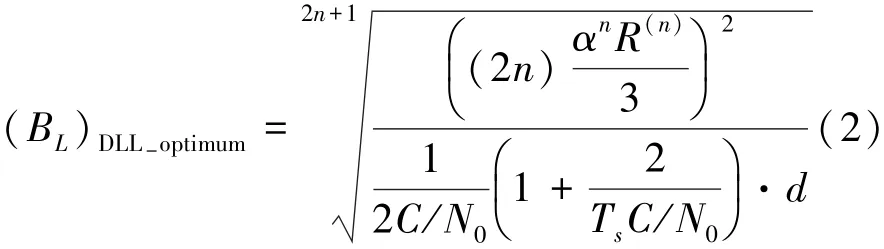
式中,n为环路阶数,R(n)为在当前环路阶数下能感应到的动态应力,Ts为积分时间,α为不同阶数环路的系数。
由于通信环境的相对稳定性,,所以除载噪比和动态应力的其他变量一般在环路设计确定之后就很少改变。因此,本文将这几个变量设为常量,仅对载噪比C/N0和动态应力2个参数测量和估计。然而载噪比C/N0和动态应力都无法直接获得,必须通过观测其他变量经过换算获取[14]。动态应力可以根据不同阶数的环路对多普勒频移参数进行处理得到,如(3)~(5)式所示。

式中,fd(t)表示t时刻的多普勒频移,f0为信号发射频率,c为光速,Ts为积分时间。载噪比C/N0可以通过即时支路的相关值,经过运算得到,如(6)式、(7)式所示。
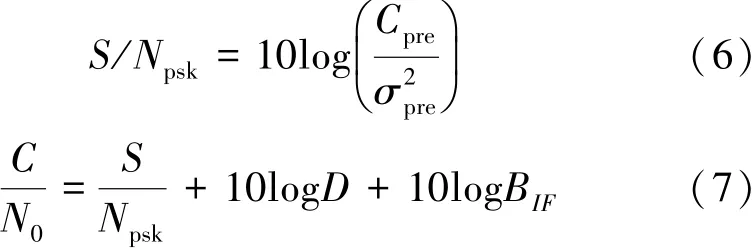
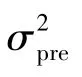
1.2CSIR粒子滤波环路跟踪算法
粒子滤波是基于贝叶斯理论和蒙特卡罗算法所衍生出来的一种对于某随机变量的最大后验估计滤波算法。粒子滤波算法在经过若干次迭代后权值会集中在少数几个样本上,使得样本退化。为了解决这个问题,现有的粒子滤波算法结合重采样技术根据先验系统的系统状态转移概率作为中间概率密度,由于新样本独立同分布所得新样本的权值均为1/N。然而对于本文所需要观测的信号载噪比与系统的动态应力来说,当信号平稳,载噪比稳定时,此时直接应用SIR算法对其进行滤波就能获得很好的估计值,然而当信号受到屏蔽,导致载噪比突然下降,另外对于接收机载体来说,载体与卫星之间的相对加加速度可视为突然产生的一个变量,这种类似于阶跃函数的信号跳变使得现有的SIR粒子滤波算法由于每个粒子点的权值会急剧减小,重采样将是一个远离于最新观测点的杂乱无章的粒子群,从而使得样本急剧退化无法实现对真实信号的估计。基于这种情况本文设计了下述条件重采样粒子滤波算法(conditional SIR,CSIR),通过设计了一种新的条件重采样机制解决了这种有阶跃状态的估计。
首先,建立的接收机加加速度的一维单变量系统
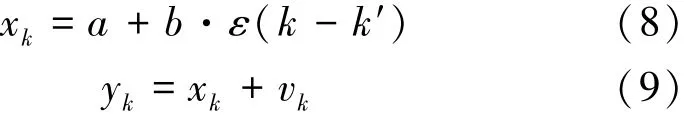
式中,xk为系统在时刻的状态,yk为xk的观测值,vk为已知的观测噪声,其概率密度服从N(0,Q),a为系统当前的加加速度大小,b为在k′时刻产生的新加加速度的方向和大小。
为了解决SIR算法对于阶跃响应的粒子严重退化的问题,本文引入限制粒子滤波进行重采样的条件,如下:
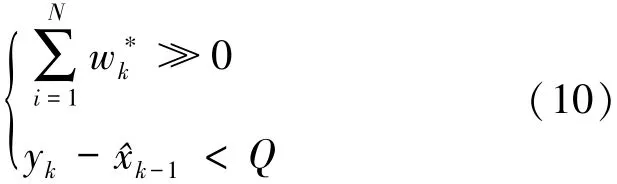
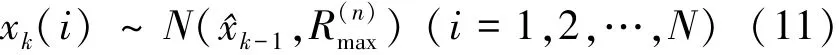
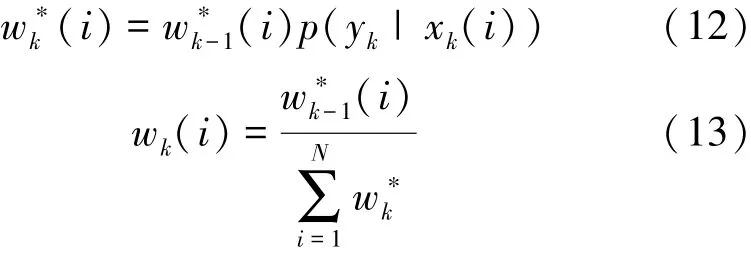
最后,根据(14)式的条件进行多项式重采样,其中u为满足(14)式且在[0,1]上的均分布中随机抽取的一个样本u~U[0,1],该过程重复进行N次,组成一个新的粒子集合xk(i)(i=1,2,…,N);并根据(15)式进行状态估计
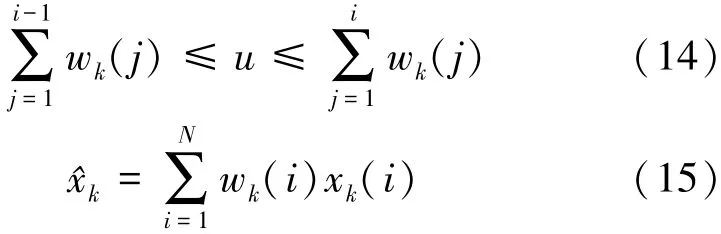
为了验证算法的正确性我们对已有的算法和提出的算法进行了仿真实验并比较了它们的性能。
2 仿真结果与分析
在仿真实验中,生成不同载噪比和动态应力条件下的卫星信号,其中仿真卫星信号的中频频率为1.405 MHz,采样率为2.046 MHz,产生的信号长度为8 s。在长为8 s的信号中,假设在开始2 s内,导航接收机与卫星之间从静止开始做加速度为2 g的相对运加速运动。在第3秒开始时,导航接收机与卫星之间开始做匀加加速度运动并维持3 s,在第6秒开始时,导航接收机与卫星开始做与之前3秒相比方向相反、大小相等的匀加加速度运动。为了比较性能,将本文所提出的算法(CSIRPF)与文献[1]所提出的定带宽锁相环(fix bandwidth,FB)跟踪环路算法,文献[5]所提出的当前值预测的变带宽锁相环(current value,CV)的跟踪环路算法,文献[6]所提出的基于卡尔曼滤波变带宽锁相环(Kalman filter,KF)的跟踪环路算法和文献[7]所提出的基于SIR粒子滤波的跟踪环路算法进行性能比较与分析,为了减小各个跟踪环路算法参数对性能的影响。5种环路跟踪算法中除环路带宽以外的各个参数完全相同,均采用闭合的三阶锁相环路,积分时间为1 ms,加加速度的更新频率为10 Hz,载噪比的更新频率为1 kHz。如图1所示为当加加速度为30 g时卫星相对于载体的速度、加速度以及加加速度的变化。
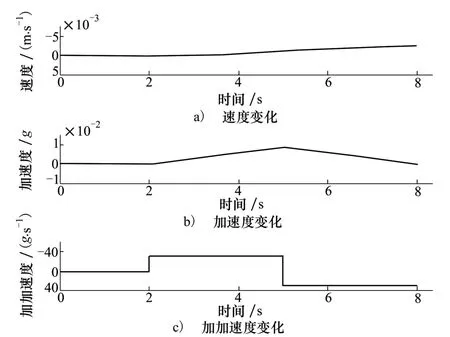
图1 仿真动态变化条件
2.1估计准确度分析
首先,对跟踪环路的估计准确度进行分析。当加加速度60 g时,4种跟踪环路估计算法对加加速度的估计仿真结果如图2所示。由于FB算法中不需要对加加速度进行计算和估计,所以在仿真中没有加入FB算法的比较。
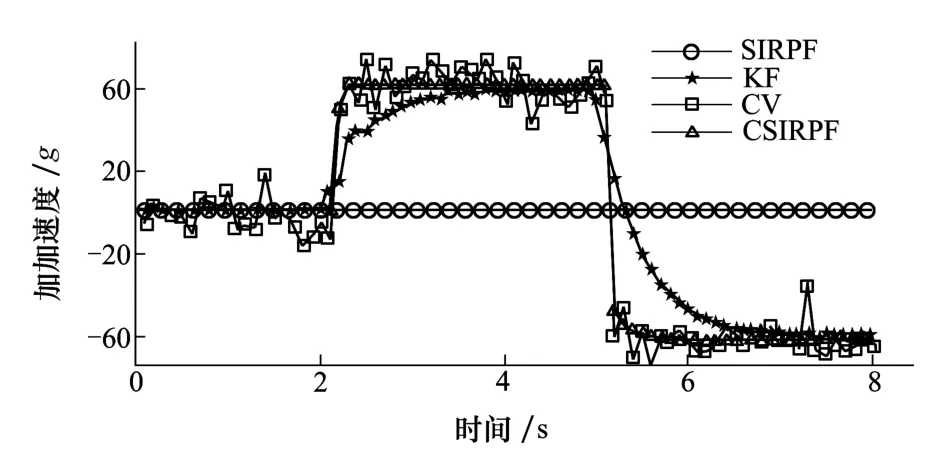
图2 对加加速度的估计结果比较
从图2中可以看出,文献[5]所提出的CV算法虽然对突变敏感但由于直接应用观测值作为估计量所以带有大量噪声,估计极不准确;文献[6]所提出的FK算法由于线性滤波特性,导致对于加加速度跳变不敏感,从而限制跟踪环路的灵敏度提高;文献[7]所提出的SIRPF算法由于跳变使得样本严重退化,所以无法对跳变后的加加速度进行正确估计;而本文所提出的CSIRPF算法中,由于加入了特定条件下的重采样算法,使得在加加速度跳变导致的样本权值退化时,通过重采样技术使样本权值快速恢复。为了进一步对比权值的影响,将本文算法与文献[7]所提出的SIRPF算法进行样本权值对比,仿真结果如图3所示。从图3中可以看出,文献[7]所提出的SIRPF算法当权值和较小时,样本与观测值的相关性较小,导致估计错误。而本文所提出的CSIRPF算法能在样本短暂急剧退化后迅速恢复,保证了数据发生阶跃突跳后依然能对其进行准确估计。
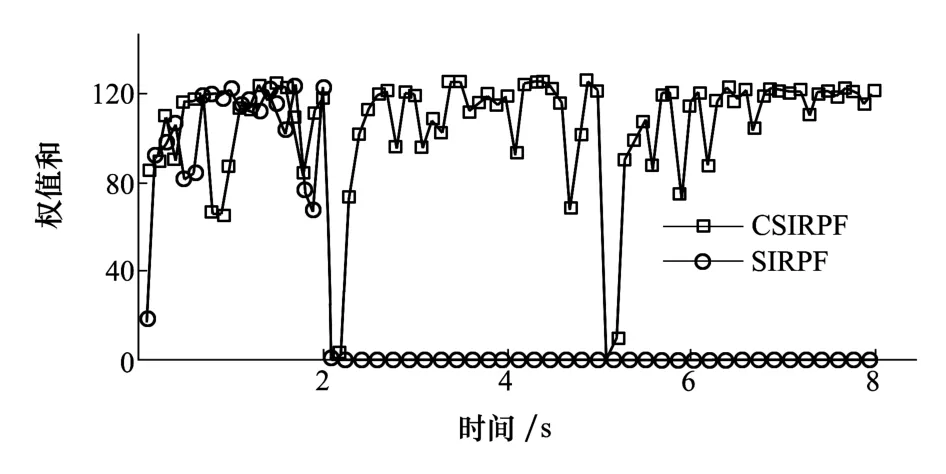
图3 样本权值退化的比较
图4a)为保持加加速度为0时,分别在不同载噪比条件下各个算法对载噪比的预测准确度,图4a)中每个点为进行100次仿真后的平均值,仿真中载噪比保持不变。可以看出4种算法在预测平稳变化的载噪比时性能基本相同。
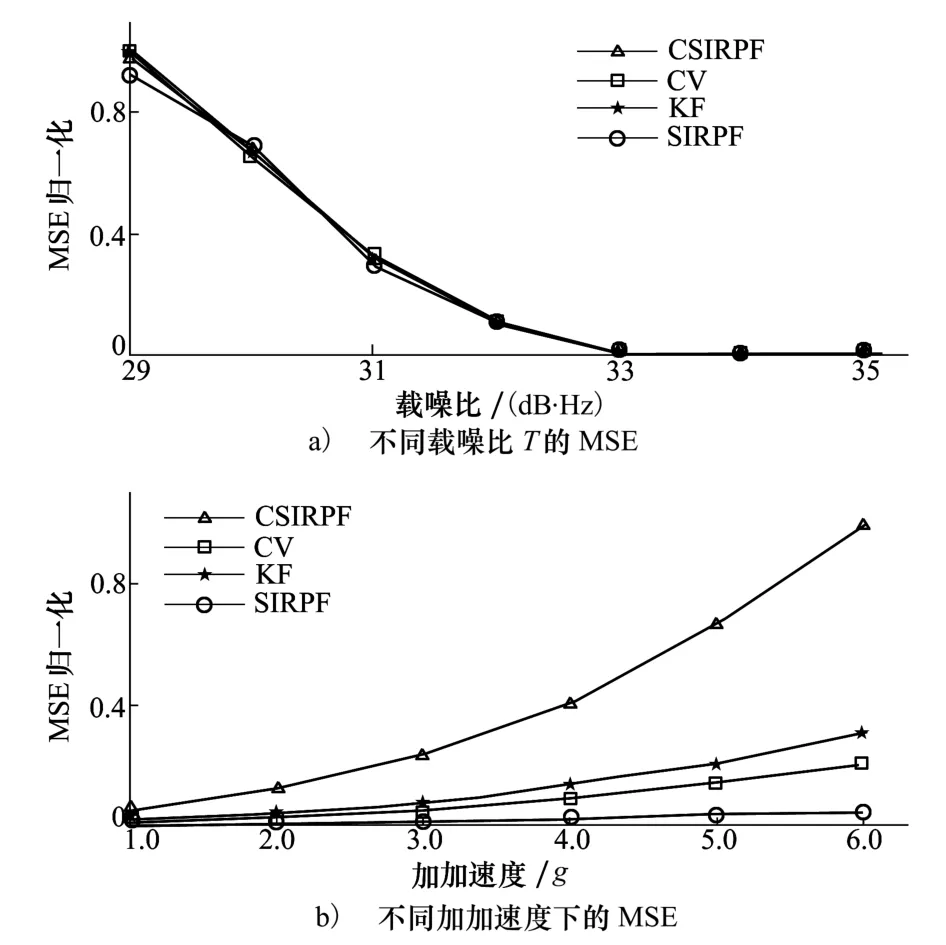
图4 预测精度的比较
图4b)所示为保持载噪比为30 dB·Hz不变的情况下,4种算法对加加速度的估计准确度,当动态应力较低时,除SIR粒子滤波算法外的其他3种算法的估计准确度都较高,但随着动态应力不断的增大,4种算法的估计性能都有下降,但本文所提出的CSIRPF粒子滤波算法的估计准确度仍明显优于其他3种算法。
2.2动态性能分析
为了对动态性能进行分析。先比较4种估计带宽算法和固定带宽算法在实际环路中的效果,将不同条件下的相同信号分别送入4种算法辅助下的动态跟踪环路中。仿真的载噪比分别选取开阔地区下平均信号载噪比35 dBHz和有轻微遮挡地区下平均信号载噪比30 dBHz,在不同加加速度条件下内环路的鉴相误差仿真结果如图5所示。
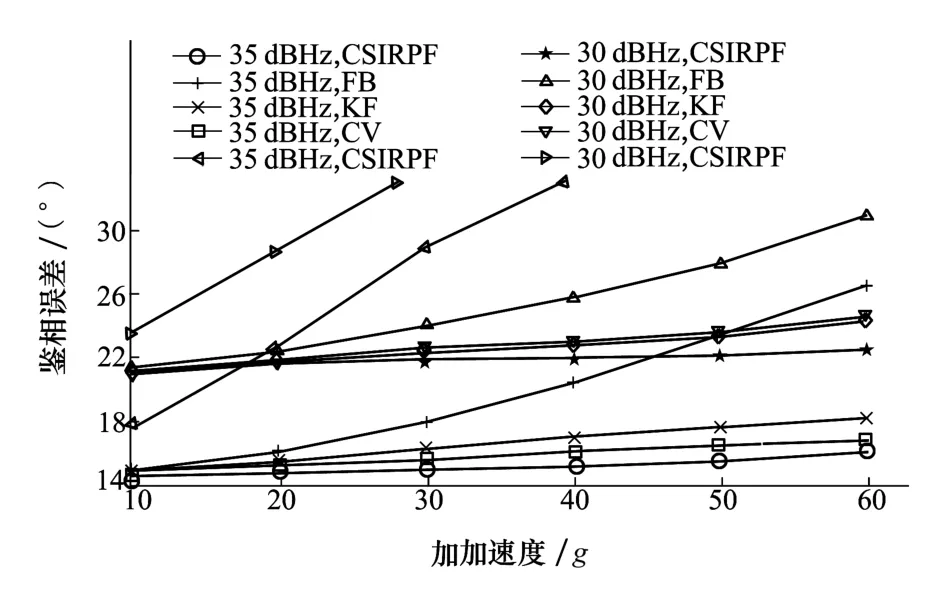
图5 跟踪环路鉴相误差的比较
从图5中可以看出,文献[7]所提出的SIRPF算法由于无法跟踪加加速度,所以加加速度的估计偏差基本处于完全错误的状态。而随着加加速度不断增大,文献[1]所提出的FB跟踪环路算法的鉴相误差急剧增加,当加加速度为60 g,载噪比为时30 dB·Hz,鉴相误差已经达到31°,解调出的数据已经出现误码的情况。而相同情况下其他3种变带宽算法的鉴相误差都明显降低,本文所提出CSIRPF算法由于对加加速度与载噪比估计更加准确,所以环路更加稳定,它的鉴相误差仅为21°,且较其他算法上升趋势缓慢。
2.3载噪比影响
首先,由于载噪比会对跟踪环路的灵敏度产生较大的影响,所以对载噪比进行仿真分析。当系统的加加速度为0时,在不同载噪比下,5种跟踪算法的性能如图6所示。从图6中可以看出,4种变带宽算法相比于定带宽算法,鉴相误差都有所降低,但是本文所提出CSIRPF粒子滤波算法并没有明显优于其他3种算法。主要由于接收机计算当前信号的载噪比是一个统计和累加的过程,所以统计出的载噪比本身已经较为平缓,并不能体现出粒子滤波算法精准与快速的预测性能优势。为此,在第3秒开始时,模拟产生的卫星信号受到遮挡而载噪比急剧下降。仿真中信号的初始载噪比为45 dB·Hz,其余仿真条件与上一仿真相同,5种环路跟踪结果如图7所示。
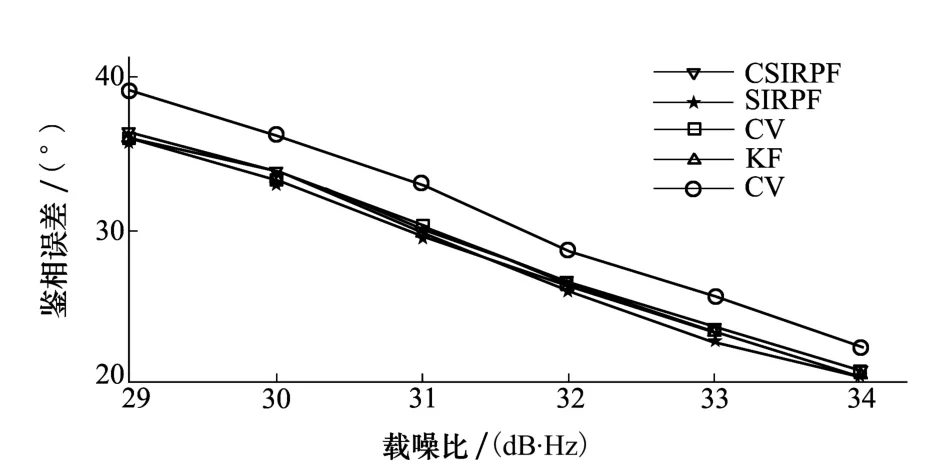
图6 无信号衰减的跟踪环路鉴相误差的比较
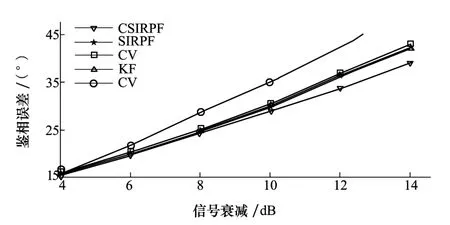
图7 信号突然衰减的跟踪环路鉴相误差的比较
从图7中可以看出随着载噪比衰减的增加,基于CSIRPF算法的跟踪环路鉴相误差逐渐优于其他4种算法,原因是由于当信号衰减时接收机计算的载噪比数据迅速变化,而CSIRPF算法相比于KF和CV算法,对变化敏感且估计准确,所以CSIRPF算法辅助的跟踪环路能更准确适应载噪比变化较大的通信环境,并在该环境下具有较高的跟踪灵敏度。
3 结 论
本文在分析卫星接收机跟踪环路的误差性能与信号信噪比、动态应力之间关系的基础上,提出了一种基于信噪比和动态应力双参数粒子滤波估计的变带宽跟踪算法。针对没有惯性器件辅助的接收机在高速动态条件下参数变化较大的特点,利用改进的CSIR粒子滤波估计接收机的动态性和接收信号的强度,并在此基础上得到自适应更新环路带宽的预测修正参数。并从估计准确度、动态性能和载噪比3个方面,将本文算法与定带宽锁相环跟踪环路算法,当前值预测的变带宽锁相环跟踪环路算法,基于卡尔曼滤波变带宽锁相环跟踪环路算法和基于SIR粒子滤波的跟踪环路算法进行性能比较与分析,仿真结果表明,本文所提出CSIRPF算法相对于其他跟踪环路算法能够提供更高的参数预测精度,从而获得最优的环路跟踪带宽并减小跟踪误差,从而提高了卫星导航接收机的跟踪灵敏度和高动态性。
[1] Yan H,Hejun Y,Yuan G.Development of the High Real-Time GPS Time Transfer Receiver[C]//Precision Electromagnetic Measurements,Rio de Janeiro,2014:150-151
[2] Chen Xi,Wang Wenjing,Meng Weixiao.High Dynamic GPS Signal Tracking Based on UKF and Carrier Aiding Technology[C]//Communications and Mobile Computing,2010:476-480
[3] Yang Y,Zhou J,Loffeld,et al.GPS Receiver Tracking Loop Design Based on a Kalman Filtering Approach[C]//53rd International Symposium ELMAR,2011:121-124
[4] Zhang Xinchun,Guo Chengjun.Optimal Design of Loop Bandwidth in GPS/INS Deeply Integration[C]//Microwave and Millimeter Wave Circuits and System Technology,2013:181-183
[5] Chai Z,Miao L,Shen J.Design of SINS/GPS Integrated Navigation System Based on Dual NiosII Soft-Core[C]//2012 IEEE Fifth International Conference on Advanced Computational Intelligence,2012:198-202
[6] Jwo J D.Optimization and Sensitivity Analysis of GPS Receiver Tracking Loops in Dynamic Environments[J].IET Proceedings of the Radar,Sonar Navigation,2001,148(4):241-250
[7] Cui S,An J,Wang Z.Design of Carrier Tracking Loops with Bandwidth Switching Adaptively[C]//Industrial Electronics and Applications,2014:841-844
[8] Nguyen T M T,Pujolle.Kalman Filter Based Bandwidth Estimation and Predictive Flow Distribution for Concurrent Multipath Transfer in Wireless Networks[C]//Network Infrastructure and Digital Content,2012:305-309
[9] AbdoulMoaty E S,Abdoul Shahid.A Particle Filter for Mutistatic Radar Tracking[C]//Aerospace Conference,2014:1-5
[10]Yanbo Bi,Rugui Yao,Ling Wang.Adaptive Noise Bandwidth Based Carrier Tracking Loop Method in Navigation Receivers[C]//Wireless and Optical Communication Conference,2013:199-202
[11]Toshiaki Tsujii,Takeshi Fujiwara,Yoshimitsu Suganuma.Development of INS-Aided GPS Tracking Loop and Preliminary Flight Test[C]//ICROS-SICE,2009:1-4
[12]唐成凯,廉保旺,张玲玲.卫星通信系统双向中继转发自干扰消除算法[J].西安交通大学学报,2015,49(2):74-79
Tang Chengkai,Lian Baowang,Zhang Lingling.An Algorithm to Eliminate Self-Interference of Bidirectional Relaying for Satellite Communication Systems[J].Journal of Xi′an Jiaotong University,2015,49(2):74-79(in Chinese)
[13]Tang Chengkai,Lian Baowang,Zhang Yi.Dual Loop Feedback Pre-Distortion in Satellite Communication[J].Journal of Systems Engineering and Electronics,2013,24(4):586-591
[14]Zhang Xiaojun,Guo Chengjun,Cao Jianshu.The Study of the Impact of High Dynamic Environment on the GPS Carrier Tracking[C]//Communications,Circuits and Systems,2013:243-246
[15]唐成凯,廉保旺,张玲玲.卫星通信中16APSK调制下带有记忆性的后置预失真算法[J].西北工业大学学报,2014,32 (6):962-966
Tang Chengkai,Lian Baowang,Zhang Lingling.Post Predistortion of 16APSK Modulation with Memory and Nonlinear Effect in Satellite Communication[J].Journal of Northwestern Polytechnical University,2014,32(6):962-966(in Chinese)
High Dynamic and Sensitivity GNSS Signal Tracking Algorithm Based on an ImProved Particle Filter
Xu Haowei,Lian Baowang,Tang Chengkai,He Wei
(Department of Electronics Engineering,Northwestern Polytechnical University,Xi′an 710072,China)
With the gradual improvement of the BeiDou satellite global positioning system and the upgrading of GPS and other satellite systems,the sensitivity of satellite receiver is also increased gradually.Weakness of navigation signals and relative motion between the satellite and the receiver are the main factors that hamper the satellite receiver sensitivity improvement.In view of this situation,we present a high sensitivity,high dynamic tracking algorithm based on particle filter algorithm.On the basis of the traditional tracking loop,through the analysis of the various factors affecting the performance of the loop,with the adaptive regulation of signal strength and dynamic stress,the algorithm adjusts the parameter of the tracking loop combined with particle filter estimates.Simulation results show that the proposed algorithm,compared with fixed bandwidth algorithm and existing adaptive bandwidth algorithm,can effectively improve the sensitivity and dynamic of tracking receiver.
algorithms,computer simulation,Doppler effect,efficiency,errors,estimation,forecasting,iterative methods,mathematical models,Monte Carlo methods,navigation,optimization,random variables, signal receivers,signal to noise ratio,target tracking,tracking(position);high dynamic,high sensitivity,particle filter
TP91
A
1000-2758(2016)02-0268-07
2015-10-09基金项目:国家自然科学基金(61101102、61473308)及中央高校基本科研业务费(31020152Y040)资助
徐昊玮(1990—),西北工业大学博士生,主要从事卫星导航、接收机设计的研究。
