基于二次距离压缩的合成孔径声呐改进距离-多普勒算法

范乃强，王英民，陶林伟

(西北工业大学航海学院，陕西西安 710072)

基于二次距离压缩的合成孔径声呐改进距离-多普勒算法

范乃强，王英民，陶林伟

(西北工业大学航海学院，陕西西安 710072)

传统的距离-多普勒算法主要应用于合成孔径成像中正侧视或小斜视角情况。在合成孔径声呐实际应用中，经常需要在较大的斜视角模式下对目标成像，而此时距离向和方位向的耦合会非常严重。在研究经典距离-多普勒算法原理的基础上，改进了适合大斜视角条件下成像的距离-多普勒算法。在放弃菲涅尔近似的条件下，提出了更精确的距离双曲线模型，并对算法进行了重新推导。提出了新的二次距离压缩方法，能更好地消除距离向和方位向的耦合。利用改进算法对成像区域中任意多个点目标上进了成像仿真。仿真结果表明，改进算法具有较高的分辨率和适中的运算量，比传统算法更适合应用于大斜视角成像。

合成孔径声呐；距离-方位耦合；二次距离压缩；泰勒级数；菲涅尔假设

在合成孔径声呐(SAS，synthetic aperture sonar)成像中，通过在声呐平台上收集目标反射回波，并对回波信号进行相干处理得到目标图像。在合成孔径成像的条带模式中，声呐通常以正侧视方式工作，即方位向波束指向与声呐平台移动方向夹角成90°。声呐波束指向可以向前或向后，通常称这种模式为斜视模式，并将斜视角定义为波束指向与声呐平台移动方向垂线之间的夹角。斜视成像能显著增大观测带宽，提高大范围成像能力，具有很强的实用意义。

随着斜视角的增大，距离向和方位向的耦合愈加严重，对成像聚焦影响较大。Wu等［1］给出了距离-多普勒(RD，range-doppler)算法方位处理的2种二次距离压缩(SRC，secondary range compression)处理方法，但其SRC调频斜率表达式并不能适用大斜视角成像。Cumming等［2］论述了斜视方式下通过距离对准和相位补偿改善成像的方位聚焦性能，但未对大斜视角条件下SRC的处理方法做详细论述。朱岱寅等［3-5］分析了大斜视角下RD算法成像分辨率下降的机理，并从距离徙动校正(RCMC，range cell migration correction)、SRC和方位聚焦3个方面推导了RD的改进算法，但遗憾的是，算法中斜距随方位时间变化的关系用近似的抛物线模型，在方位聚焦性能方面具有局限性，从而限制了成像的分辨率。Jin等［6］提出以多普勒中心和参考距离上的固定参数进行SRC，并且可以和第一次距离压缩合并处理。该算法以菲涅尔假设为基础，当方位波束较宽或斜视角较大时，距离方位耦合没有得到精确的校正，不适合应用于以宽带信号为特征的SAS成像中。

本文在传统RD算法的基础上，采用了更加精确的双曲线模型来描述斜距随方位时间的变化关系。针对在大斜视角条件下时频间的非线性关系，适时调整了用于距离徙动校正和方位匹配滤波的距离变量，消除较大的方位向和距离向耦合。放弃了相位方程的近似推导，采用了更加精确的推导公式，并在二维频域中通过相位相乘来实现SRC，使算法具有了处理合成孔径声呐较大斜视角数据的能力。

1　斜视合成孔径成像回波模型分析

在合成孔径声呐成像中，斜视角是重要的参数之一。斜视角为0°时，成像为正侧视模式，斜视角大于0°时，距离向和方位向会产生一定的耦合，因此应该考虑斜视角对成像的影响。

1.1斜视SAS回波几何模型

图1为SAS斜视模式下成像的空间几何模型。其中，θsq是斜视角，h是拖鱼距离海底的高度，设拖鱼的移动速度为V，RB为目标至拖鱼航线之间的垂直距离，R0为目标至拖鱼的斜距，tm为方位向时间， tc为拖鱼处于合成孔径中心的时刻。

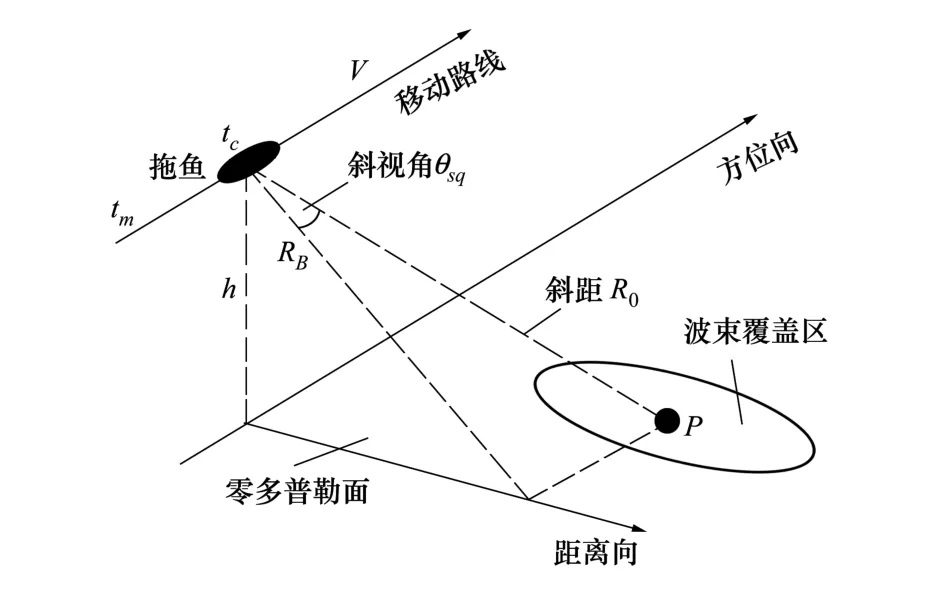
图1　SAS斜视成像空间几何模型

由图1的几何关系可得，瞬时斜距

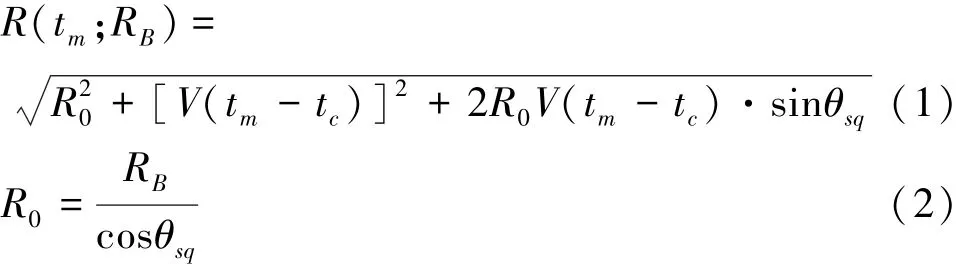
1.2点目标回波信号

设SAS发射线性调频信号为

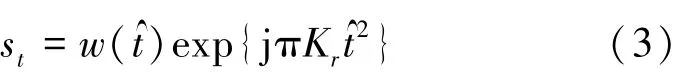
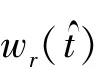
2　RD算法分析

经典RD算法主要针对处理正侧视(θsq＝0)或小斜视角的数据，算法将距离向和方位向解耦变换为距离向和方位向的2个一维操作，并采用频域快速相关算法提高了运算速度。

2.1算法的主要步骤

1)距离向FFT、距离压缩处理和距离向IFFT根据(3)式，对距离向作匹配滤波的系统匹配函数为

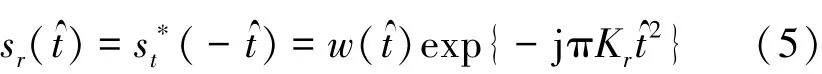
为了减少计算量，在距离频域(fr)方位时域(tm)中完成距离向的匹配滤波。对于距离向，在时域和频域之间的变换采用快速傅里叶变换(FFT)和逆傅里叶变换(IFFT)。可以得出距离压缩后信号为

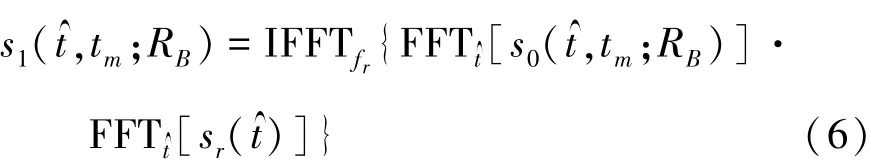
为了方便推导，不妨设距离向为矩形窗，(3)式的接收信号通过上述处理后，可得

式中，A1为距离压缩后目标信号的幅度，Δfr为线性调频信号的频带。

2)方位向傅里叶变换

对于最近距离为RB的点目标P，在波束较窄的情况下，波束扫过点目标的合成阵列长度比RB要小的多，即Vtm≪RB，此时，利用菲涅尔近似，可将RB与tm的关系表示为

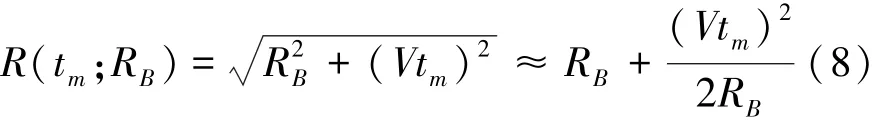
式中，第2项为距离徙动值。将(8)式代入(7)式，距离快时间⁃方位慢时间域信号可表示为

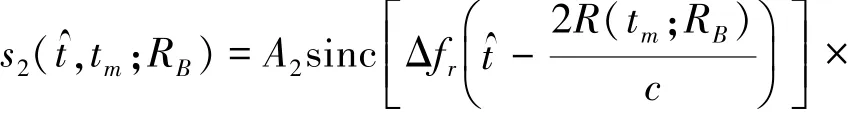
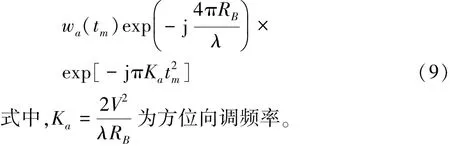
方位FFT的信号为

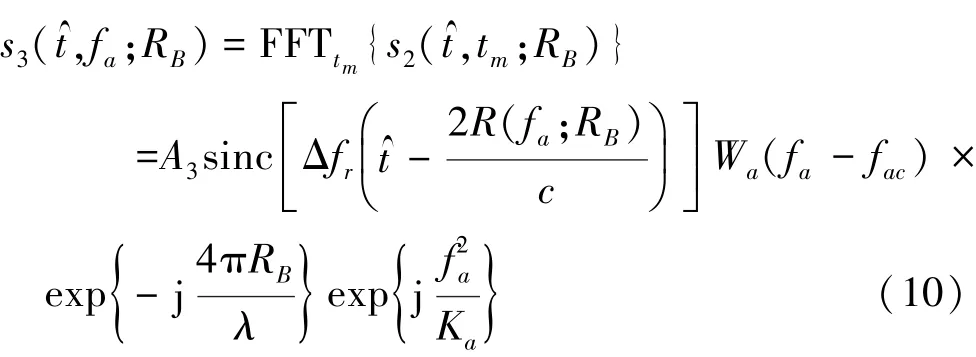
式中，fa为方位向频率，fac为多普勒中心频率。

3)距离徙动校正

在距离多普勒域中通过基于sinc函数插值处理实现距离徙动校正，解除距离向和方位向的耦合［7］。经过距离徙动校正后，信号变为

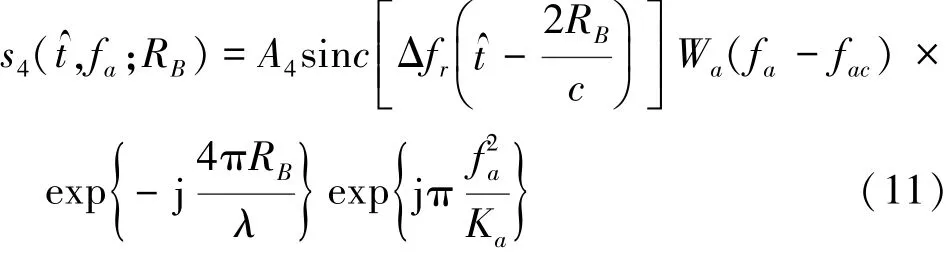
4)方位压缩和方位向IFFT

方位向匹配滤波函数为

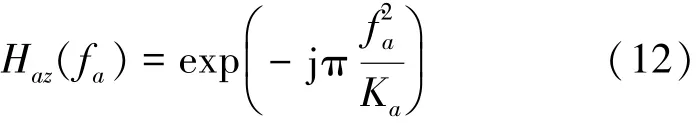
式中，与距离向匹配滤波相同，方位向匹配滤波也可在多普勒域进行，匹配滤波后的输出为

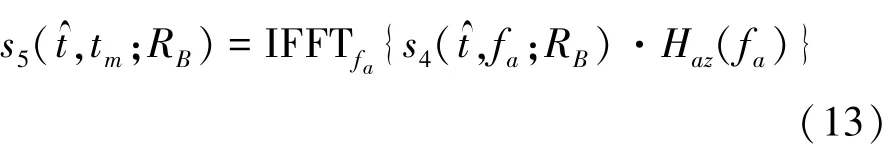
5)点目标成像

经过以上步骤的处理，可以得出点目标的成像结果为

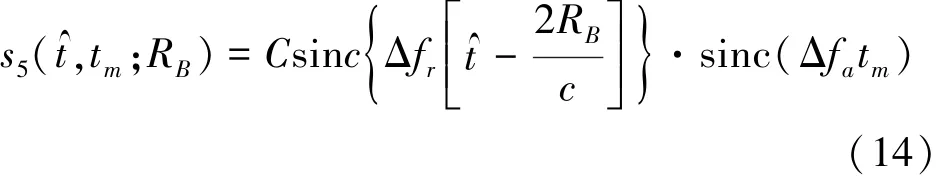
式中，Δfr为发射信号带宽，Δfa为多普勒带宽，其中，Δfa＝KrTs，Ts为合成孔径时间。

2.2斜视模式下RD算法与二次距离压缩问题

在斜视模式以及大测绘带成像时，RD算法通常引入二次距离压缩(SRC)处理。如图1所示，假设Vtm≪R0，在Vtc附近利用泰勒级数对(1)式展开，省略V(tm－tc)的三次项以及高次项，得(1)式的近似式为

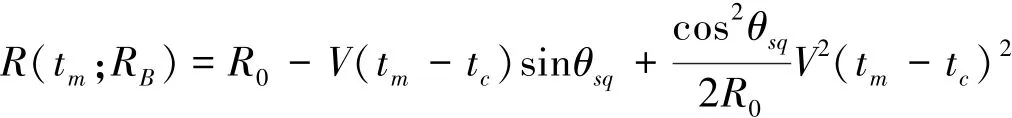
拖鱼与成像目标P之间的瞬时斜距可以近似表示为

对(16)式作方位向FFT变换，并利用驻定相位定理，可得

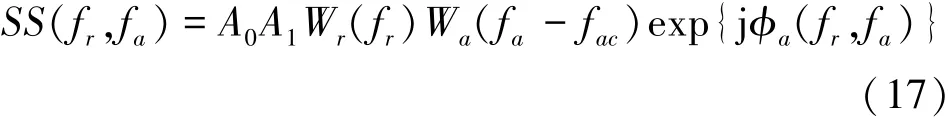
式中Wa(fa－fac)是以多普勒中心频率fac为中心的方位频谱包络，ϕa(fr，fa)是傅里叶变换后的相位角，可以得出ϕa(fr，fa)的表达式为

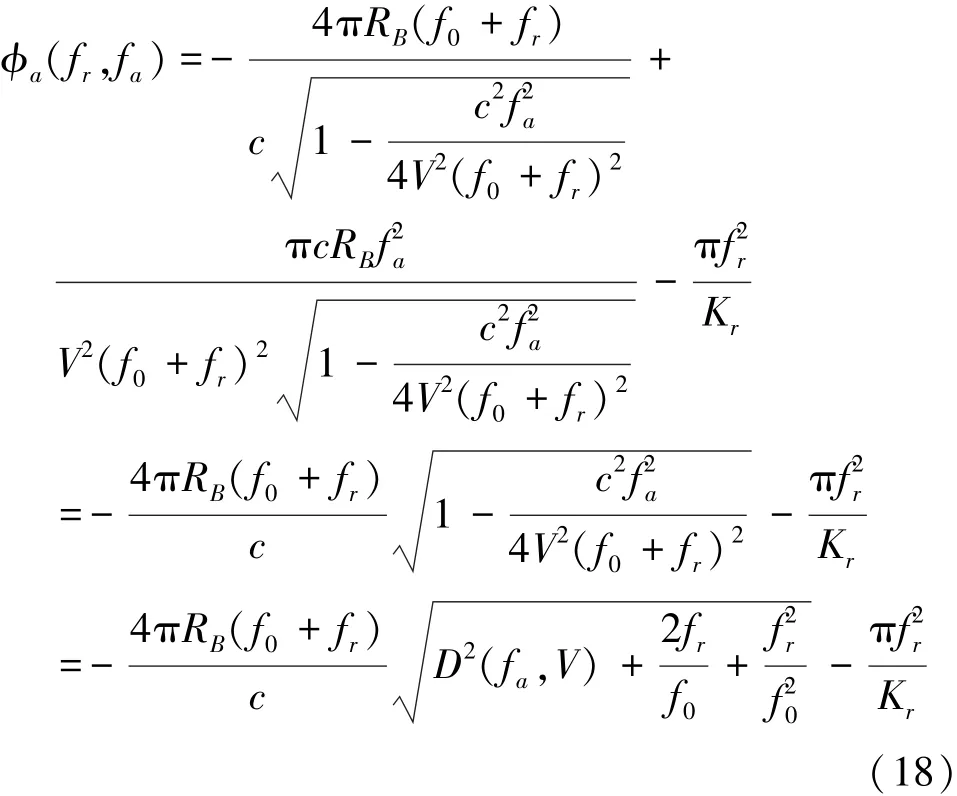
将(18)式中根号下的式子展开成fr的幂级数并保留二次项，可得

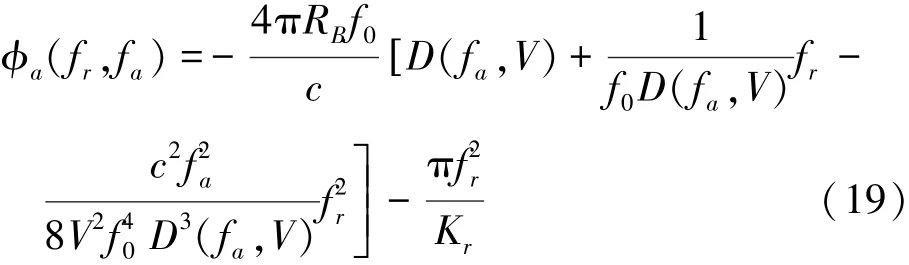
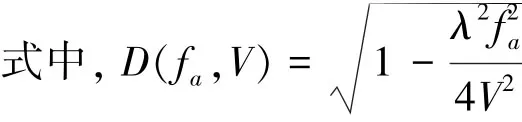
2.3经典RD算法的局限性分析

在正侧视或低斜视角模式下，距离等式被近似成为时间的抛物线方程式，如(8)式所示。时间频率间的关系为一一对应的线性关系，随着斜视角的增大，时间频率间的对应关系是非线性的。这种非线性关系给SAS处理带来以下影响：

1)波束单位时间内扫过点目标的横向距离Vtm及合成阵列长度Ls＝RBθBW(正侧视模式)与RB相比均可比拟，不满足窄波束条件，不能简单的利用Vtm≪RB的关系做近似，此时Fresnel近似不再成立。

2)大斜视角模式下，回波会引入较强的距离向和方位向耦合，需要通过二次距离压缩处理来校正耦合造成的散焦。但是传统的二次距离压缩没有考虑方位调频率、多普勒带宽在内的方位向参数随斜视角的变化关系，在处理大斜视角和宽测绘带的SAS时，二次距离压缩处理不彻底，成像效果一般。

3　改进RD算法

为了消除大斜视角条件下的距离向和方位向耦合，改进的RD算法采用了更加精确的距离方程来描述声呐至成像目标的斜距随方位时间的变化关系，并采用更加精确的距离向和方位向匹配滤波器，通过在二维频域中采用二次距离压缩处理和补偿高次耦合项，以此来校正耦合造成的图像散焦。算法的处理步骤主要包括距离压缩、二次距离压缩(SRC)、三次相位补偿、距离徙动校正和方位压缩。如图2所示，在二维频域完成二次距离压缩后，改进算法通过补偿二维频谱中距离频率的三次相位项，可以有效解决距离向压缩旁瓣不对称问题，使图像获得良好的聚焦。

3.1距离方程的改进

在大斜视角下，采用更加精确的双曲线距离模

3.2RCMC的改进

RCMC在距离多普勒域中进行，距离徙动为

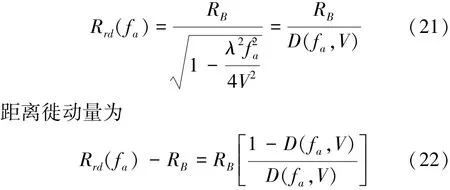
将(21)式中的二次根式展开并忽略fa二阶以上项， (22)式将变为低斜视角下的距离徙动量，因此该式子具有普遍适用性。

3.3方位匹配滤波器的改进

在经典RD算法中，方位匹配滤波器如(12)式所示。在大斜视角模式下，改进后的方位匹配滤波器为

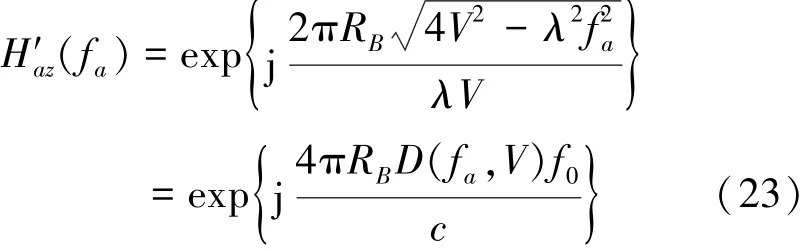
同样，展开D(fa，V)并忽略fa二阶以上项，则方位匹配滤波器变为(12)式，因此该式子在斜视模式下同样具有普遍适用性。

3.4二次距离压缩（SRC）改进

1)二次压缩处理

在距离多普勒域中，首先使用调频率为Kr的滤波器进行初级压缩，然后再使用调频率为Ksrc的次级滤波器进行二次距离压缩。根据(19)式，二次压缩滤波器可设计为

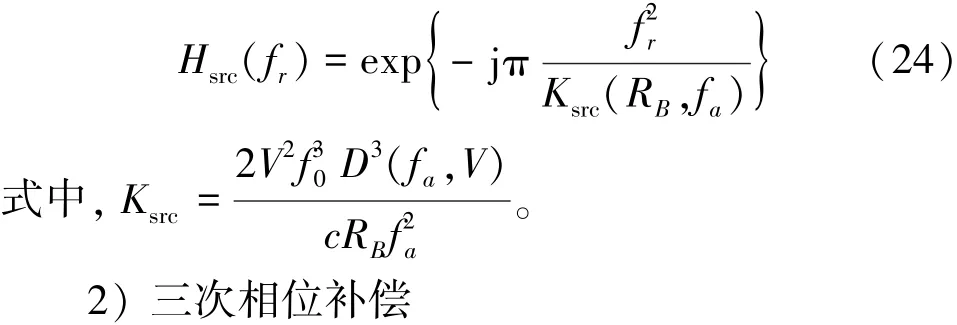
在(18)式中，展开成fr的幂级数并保留三次项可得

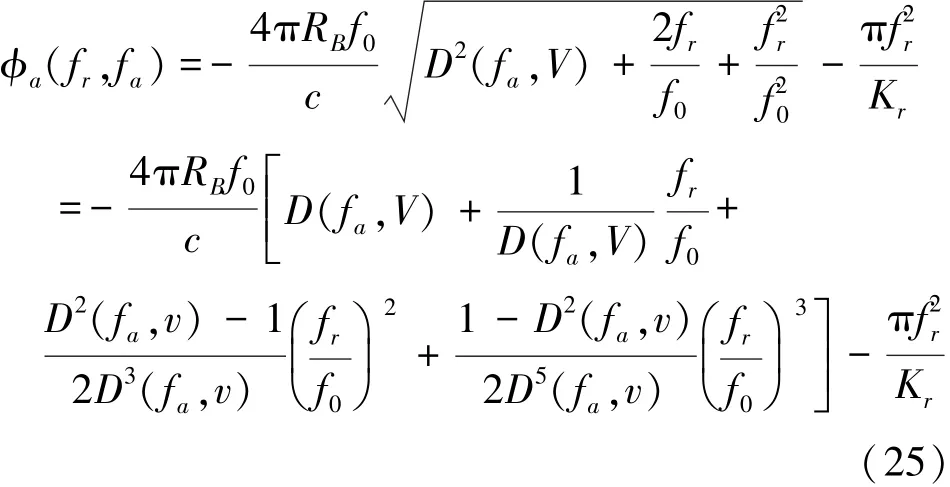
式中，括号中第四项是距离频率fr的三次函数，在斜视角较小的情况下，方位频率fa在多普勒零频附近，三次相位项非常小，可以忽略。但是在大斜视角下，多普勒中心频率远离零频，方位频率fa的值很大，不能忽略，残留的奇次相位误差将造成压缩旁瓣的不对称［8］，且斜视角越大，不对称越严重。因此必须做三次相位补偿。三次相位补偿的匹配滤波函数可以设计为

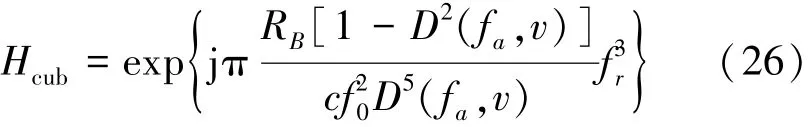
改进后的二次距离压缩处理RD算法处理流程如图2所示。

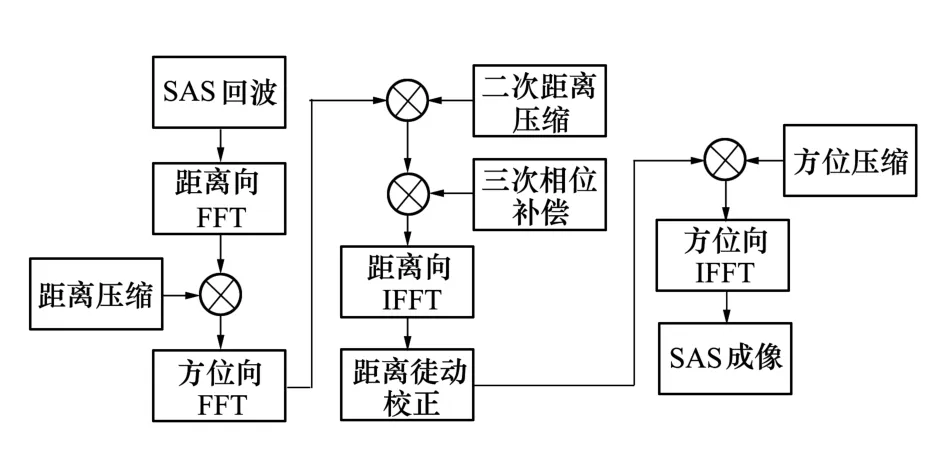
图2　斜视模式改进RD算法流程

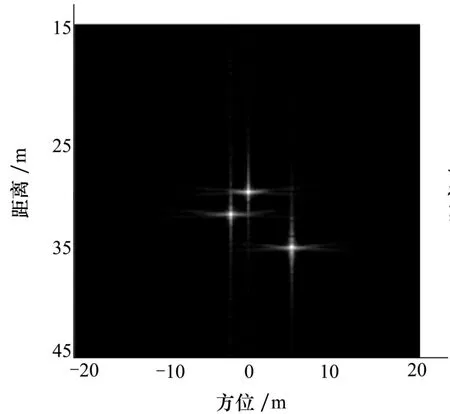
图3　正侧视模式成像

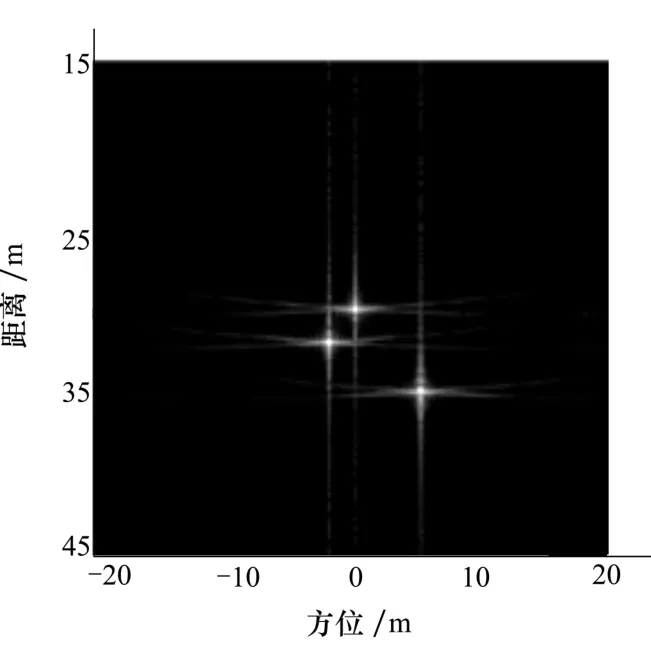
图4　斜视角为5°时传统RD算法成像

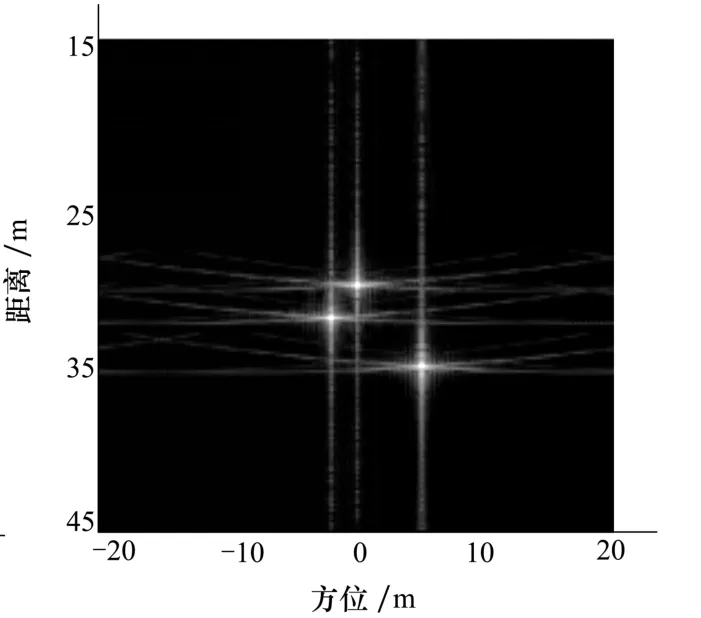
图5　斜视角10°时传统RD算法成像

4　计算机仿真及算法性能分析

4.1点目标仿真参数

目标由3个散射点组成，其坐标设定为(0， 30)，(5，35)，(－2，32)，其中横坐标为方位向，纵坐标为距离向。分别在正侧视、斜视模式下运用经典RD算法对3个散射点进行成像，然后利用改进RD算法在相同条件下的斜视模式对3个散射点成像。

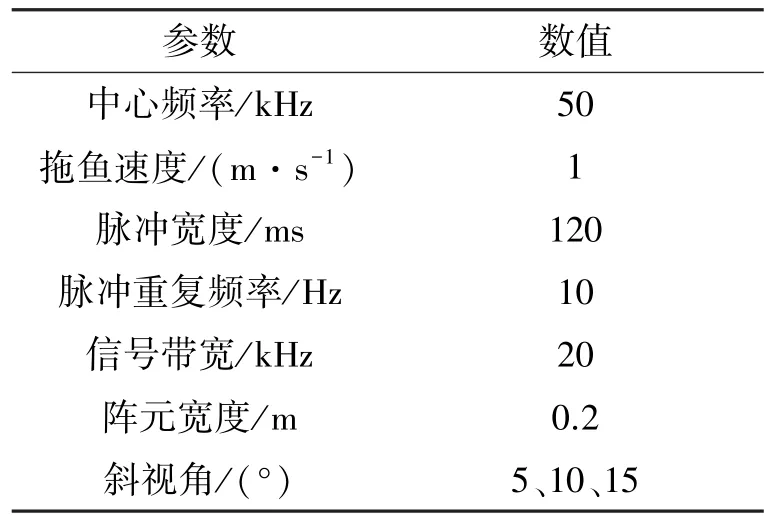
表1　点目标仿真参数设置

4.2点目标仿真分析

图3为正侧视模式下，利用经典RD算法对三点目标的成像效果。可以看出，在正侧视模式下，不需要进行二次距离压缩处理，经典RD算法成像效果较好。图4为斜视角为5°时，经典RD算法的成像效果。对比正侧视的成效聚焦效果可知，由于斜视角的存在，距离向和方位向的耦合导致点目标成像有一定的散焦。图5、图6为斜视角为10°、15°时的成像效果，由成像结果可以看出，随着斜视角的逐渐增大，距离向和方位向的耦合程度越来越严重，经典RD算法未能彻底消除耦合，从而导致成像散焦较为明显。

图7～图9分别为采用本文改进算法在斜视角为5°、10°、15°时的成像效果。在相同斜视角下对比两种算法，改进RD算法消除距离向和方位向的耦合更为彻底，从而使得图像得到了很好的聚焦效果。

对点目标仿真结果的3dB主瓣宽度、积分旁瓣比(integrated side-lobe ratio，ISLR)、峰值旁瓣比(peak side-lobe ratio，PSLR)在未对匹配函数进行加窗的条件下进行分析对比。对于成像结果，一般要求ISLR＜－10 dB，PSLR＜－15 dB。表1给出了3个点目标在不同斜视角条件下距离向和方位向的ISLR和PSLR。表2为经典RD算法和本文改进算法在点目标(5 m，35 m)处的PSLR和ISLR的性能对比结果。由以上结果可以得出，本文改进算法具有更好的性能指标。

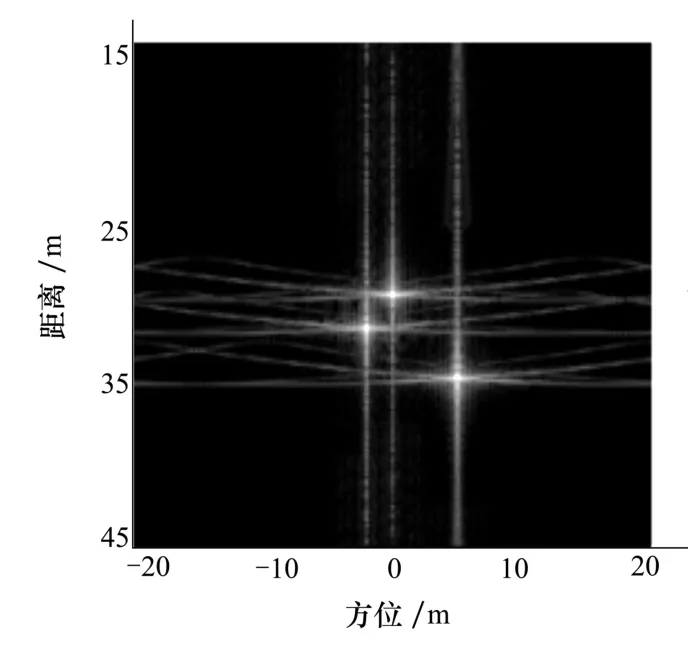
图6　斜视角15°时传统RD算法成像

图7　斜视角为5°时本文改进RD算法成像

图8　斜视角为10°时本文RD算法成像

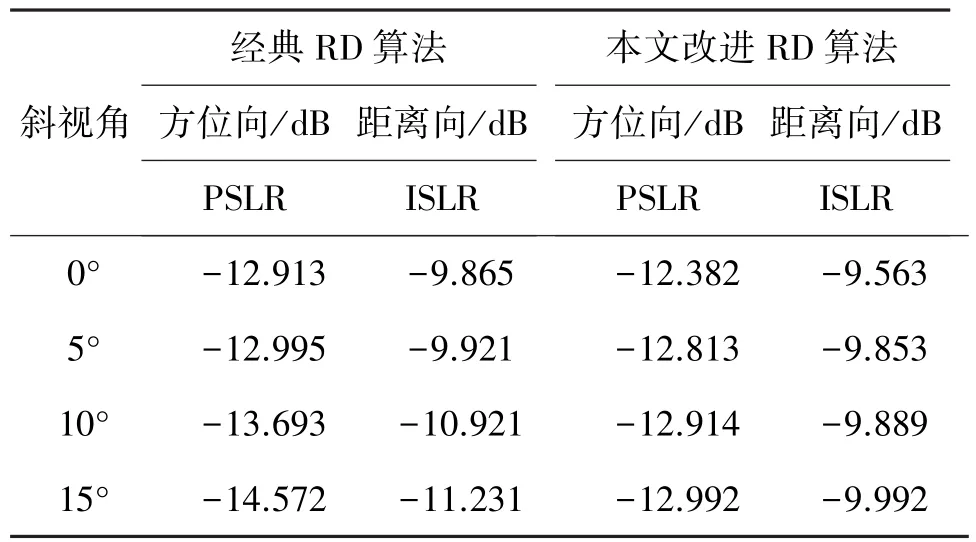
表2　经典RD算法和本文改进算法对点目标（5 m，35 m）的成像性能对比

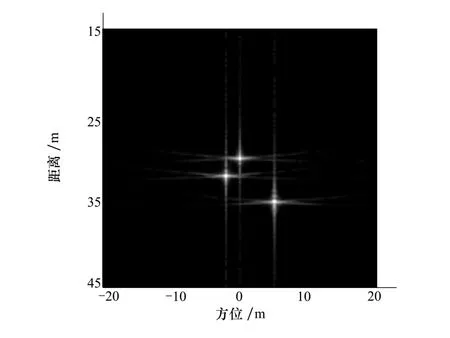
图9　斜视角为15°时本文RD算法成像

5　结 论

在大斜视角的合成孔径成像中，距离向和方位向之间的耦合更加严重，导致图像散焦，成像质量严重下降。文中采用了更加精确的双曲线模型来描述声呐平台到散射点的瞬时距离，并推导了高阶二次距离压缩的理论公式，采用二次距离压缩与三次相位补偿同时处理的方法，减小了相位误差，降低由于校正耦合而带来的图像散焦。对仿真的成像结果分析表明，本文提出的改进RD算法是正确有效的。由于合成孔径声呐中相对合成孔径雷达对成像算法的应用条件更加苛刻，因此，在近似的条件下，该算法也可以应用到合成孔径雷达成像中，具有较广的适用性。

［1］ Wu C.A Digital System to Produce Imagery from SAR Data［C］//AIAA Conference：System Design Drive by Sensors，1976

［2］ Cumming Ian G，Bennent J R.Digital Processing of SEASAT SAR Data［C］//IEEE 1979 International Conference on Acoustics，Speech and Signal Processing，Washington D C，1979：2-4

［3］ 朱岱寅，朱兆达，谢球成，等.机载SAR斜视区域成像研究［J］.电子学报，2002，30(9)：1387-1389

Zhu Daiyan，Zhu Zhaoda，Xie Qiucheng，et al.Studies on Airborne Squint-Looking SAR Patch-Mapping［J］.Acta Electronica Sinica，2002，30(9)：1387-1389(in Chinese)

［4］ 王亮，练有品，黄晓涛，等.大斜视角与大波束角SAR成像比较［J］.电子学报，2006，34(9)：1672-1676

Wang Liang，Lian Youpin，Huang Xiaotao，et al.Comparison of Large-Squint and Large-Beamwidth SAR Imaging［J］.Acta Electronica Sinica，2006，34(9)：1672-1676(in Chinese)

［5］ 汪亮，禹卫东.机载SAR大斜视角成像算法及其性能分析［J］.电子信息学报，2006，28(3)：502-506

Wang Liang，Yu Weidong.Imaging Algorithm and Analysis of Airborne SAR in Large-Squint Mode［J］.Journal of Electronics＆Information Technology，2006，28(3)：502-506(in Chinese)

［6］ Jin M，Wu C.A SAR Correlation Algorithm Which Accommodate Large-Range Migration［J］.IEEE Trans on CE，1984，22 (6)：592-597

［7］ 张学波，唐劲松，张森，等.四阶模型的多接收阵合成孔径声呐距离-多普勒成像算法［J］.电子信息学报.2014，36(7)：1592-1598

Zhang Xuebo，Tang Jinsong，Zhang Sen，et al.Four-Order Polynomial Based Range-Doppler Algorithm for Multi-Receiver Synhetic Aperture Sonar［J］.Journal of Electronics＆Information Technology，2014，36(7)：1592-1598(in Chinese)

［8］ Chang C Y，Jin M，Curlander J C.Squint Mode SAR Processing Algorithm［C］//International Geoscience and Remote Sensing Symposium(IGRARSS′89)Uancouver，BC，Canada，1989

ImProved Range-DoPPler Algorithm for Processing Synthetic APerture Sonar Data Based on Secondary Range ComPression

Fan Naiqiang，Wang Yingmin，Tao Linwei
(Northwestern Polytechnical University，Xi′an，710072)

The traditional Range-Doppler algorithm is mainly used in side looking or small squint angle mode of synthetic aperture imaging.In application of synthetic sonar，the large squint angle imaging is often required and the range-azimuth coupling is serious.On the basis of studying the principle of the classical range Doppler algorithm，it improved the imaging algorithm in large squint mode.A more accurate range hyperbolic model is proposed and then the algorithm is deduced under the condition of abandoning the Fresnel assumption.The new secondary range compression method proposed in the paper is expected to eliminate effectively the range-azimuth coupling. Any point target is simulated in imaging region by using the improved algorithm.The simulation conclusion showed that the improved Range-Doppler algorithm had higher resolution and moderate computational complexity as compared with the traditional algorithm

synthetic aperture sonar；range-azimuth coupling；secondary range compression；taylor series；fresnel assumption

TN911.7

A

1000-2758(2016)02-0201-07

2015-10-27基金项目：国家自然科学基金(51209173)资助

范乃强(1978—)，西北工业大学工程师，主要从事水声信号处理、声呐成像研究。