非全包裹超空泡航行体建模与反演变结构控制

李洋，刘明雍，张小件，彭星光

(西北工业大学航海学院，陕西西安 710072)

非全包裹超空泡航行体建模与反演变结构控制

李洋，刘明雍，张小件，彭星光

(西北工业大学航海学院，陕西西安 710072)

超空泡航行体动力学系统存在高度非线性及多变量耦合等问题，非全包裹超空泡使其受力更为复杂，给控制系统设计造成诸多困难。针对超空泡航行体的以上特点，开展了对非全包裹超空泡航行体控制系统的研究，在通过受力分析建立其动力学模型基础上，设计了超空泡航行体的反演变结构控制器，并证明了系统稳定性。仿真结果验证了该控制器对超空泡航行体稳定航行及跟踪控制的有效性。

非全包裹；超空泡航行体；建模；反演变结构控制

因利用一层气体包裹航行体，使其仅有很小部分与水接触，减少了附加质量和阻尼力矩，超空泡技术为水下航行体带来高速航行可能性的同时，也使航行体对外界干扰更加敏感，动力学建模、制导与控制等方面更加困难［1-6］。

超空泡根据空泡形状的不同可以分为全包裹与非全包裹两大类。目前，研究大多集中于全包裹超空泡技术中。Vanek等［1］对超空泡航行体纵向动力学模型非线性项里的滑行力进行重点研究，并通过滚动时域控制对航行体进行了跟踪控制的研究。Dzielski［2］建立了全包裹超空泡航行体的非线性模型并利用反馈线性化进行处理。Mao等［3］考虑了尾舵效率n的不确定性，将其视为未知参量并通过自适应控制的方法实现对超空泡航行体的跟踪控制。Kirschner等［4］研究了空泡结构对航行体动力学模型的影响。Yu等［5］利用有限元方法对超空泡的形成，航行体在机动过程与空泡的相互作用等内容进行了研究。Li等［6-7］考虑空泡变化的时延效应，并进行了相关试验。Mokhtarzadeh等［8］研究了3种不同形状空化器对航行体稳定性的影响，以及不同空化数对空泡形成的影响，同时也对上述不同情况下航行体产生的滑行力进行了分析和研究。目前，研究大多集中于全包裹超空泡技术中，而对非全包裹超空泡的研究还十分欠缺，仅Kim等［9］提到超空泡形成的过渡阶段等相关内容，但其研究重点在于从物理角度出发，研究在非全包裹超空泡的状态下，航行体的受力情况，对该状态下的航行体控制系统研究较少。非全包裹超空泡，即空泡不完全包裹航行体，而闭合在航行体尾部之前，这就造成航行体尾部仍受到浮力作用［9］。在实际航行中，当航行速度下降或者空化器通气不足时，空泡自然会缩短，非全包裹超空泡航行不可避免。与全包裹超空泡相比，非全包裹超空泡状态下的航行体受到的阻力增加，因航行体处于2种介质之中受力更为复杂。因空泡外形改变，不再适用已有全包裹超空泡的动力学模型，有必要对非全包裹状态下航行体的动力学特性进行研究。

本文以非全包裹超空泡航行体为研究对象，首先对该状态下的航行体进行受力分析，进而建立动力学模型并分析其零输入状态响应性能；然后设计了一种反演滑模控制器来完成对航行体的复合控制；最后通过仿真验证，表明该控制系统具有较好的控制效果。

1　非全包裹超空泡航行体动力学建模

本文研究模型为无尾舵航行体，利用头部空化器偏转及尾部直接侧向力控制航行体姿态，且其上下、左右均相互对称，不考虑横滚的情况下，运动可解耦为纵平面及水平面2个平面运动［10］。以纵平面运动分析为例，其头部空化器可偏转一定角度，利用合理的通气及航行体外形设计使空泡闭合于航行体尾部即直接侧向力作用前端。如此，该航行体受力如图1所示。分为头部空化器阻力且与尾部推力相同，空化器升力，自身重力，直接侧向力，尾部浸入海水部分所受浮力以及尾部上下表面所受的压力差。

图1　超空泡航行体受力分析图

考虑头部空化器为圆盘形，主体前1/3部分为圆锥，后2/3部分为圆柱，总长度用L表示［7］。描述航行体运动的坐标系取重心处为原点o，三轴分别为沿发射方向水平的x轴，垂直于x轴水平向右的y轴及垂直平面竖直向下的z轴。其中航行体质量为m，x轴方向上速度为V，绕横轴转动惯量为Jy，空化器相对于重心的位置为lc，直接侧向力作用点相对于重心的位置为lf，且分别为：

与全包裹超空泡航行体的情况类似，作用在空化器上的升力及阻力：

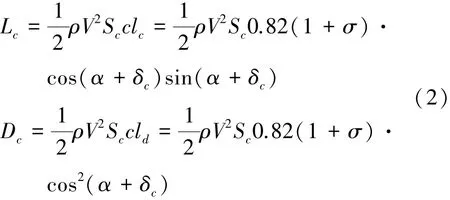
式中，ρ为海水密度，Sc为空化器的最大横截面积［10-11］。

当空化器发生偏转时，将作用在空化器上的流体动力分解为体坐标系各轴方向的分力［8］为：若记体坐标系下，空化器的坐标为(xc，0)，则空化器上的升力相对航行体重心的转动力矩［18］为：

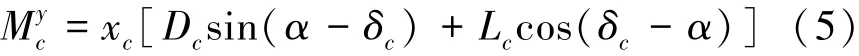
尾部压差主要来自机动时，因与水接触的角度及截面积不同而造成的，这里近似以尾舵的计算公式来计算：

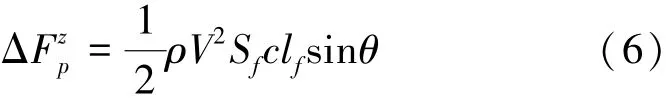
式中，Sf为受力面的最大横截面积，clf为升力系数。需要注意的是，此处的压差不同于全包裹超空泡中的尾部滑行力，滑行力是指因航行体尾部部分伸出空泡，与水接触，而其另一侧仍在空泡中时受到的一种流体动力。本文所讨论的尾部压差来源于直接侧向力作用时，全部侵入水中的航行体尾部所受到的流体动力。

因航行体在超空泡航行状态下，速度较高，机动时间较短，故可在小时间范围内忽略其速度变化，认为速度是恒定的［12］，推力和阻力保持平衡，可以得到下面的二维纵向动力学方程：

选取深度z，纵向线速度w，俯仰角θ，纵向角速度q为状态向量，空化器偏转角δc及直接侧向力Fv作为系统输入，另考虑纵向的2个运动方程［13］：

可得关于纵平面内线性化的状态方程：

2　模型开环特性验证

对已建立的非全包裹超空泡航行体系统模型进行开环系统零输入状态响应仿真分析，航行体纵向模型系统参数［5，8，12，15］分别为：重力加速度g＝9.81 m/s2，空化器半径r＝0.019 m，航行体半径R＝0.05 m，航行体总长L＝1.8 m，航行体速度V＝70 m/s，空化数σ＝0.03，航行体质量m＝2 kg，转动惯量Jy＝0.54 kg·m2。

系统初始状态设为［20 0.1 0 0］T，仿真结果如图2所示。

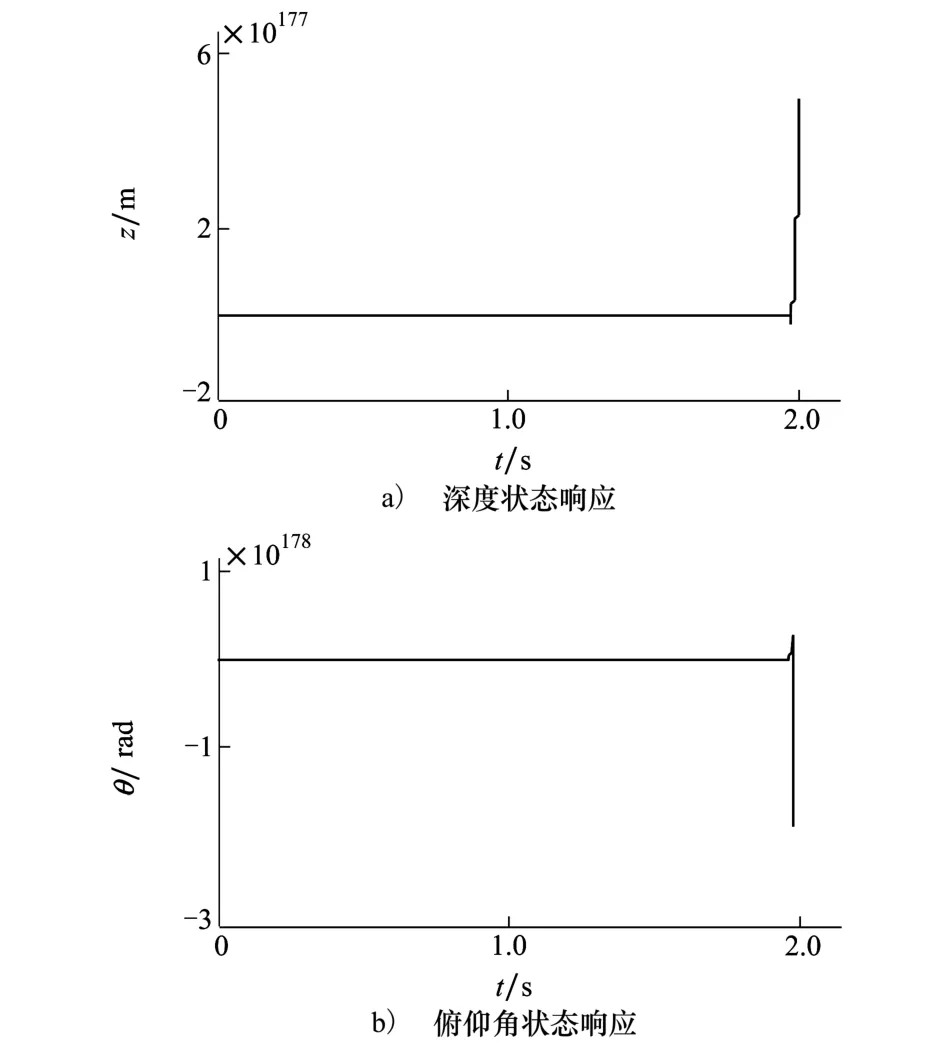
图2　系统零输入状态响应

由图中可以看出，系统在零初始状态下的系统状态响应，因空化器无偏角，造成头部空化器所受升力为零，在重力作用下，在2 s附近迅速发散。俯仰角的变化剧烈，在1.9 s以后w和θ幅值急剧震荡并最终发散，无法实现稳定航行。实际应用中，发射该航行体的有效距离较短，其航行速度在超空泡的状态下相对较高，导致其机动、姿轨控制的调节时间很短，几乎都是在毫秒级完成姿轨控制［7］，因此必须对航行体的机动施加闭环控制。

3　反演变结构控制器设计

3.1问题描述

非全包裹超空泡航行体的复合控制是一个涉及多参量，多输入多输出的复杂控制系统［15］，反演控制的设计方法可以有效简化问题［11］，但传统的反演控制方法无法保证鲁棒性，通过引入滑模项，可克服干扰，保证控制器的鲁棒性［16］。

为简要说明问题，在不影响理解的情况下将(9)式改写：

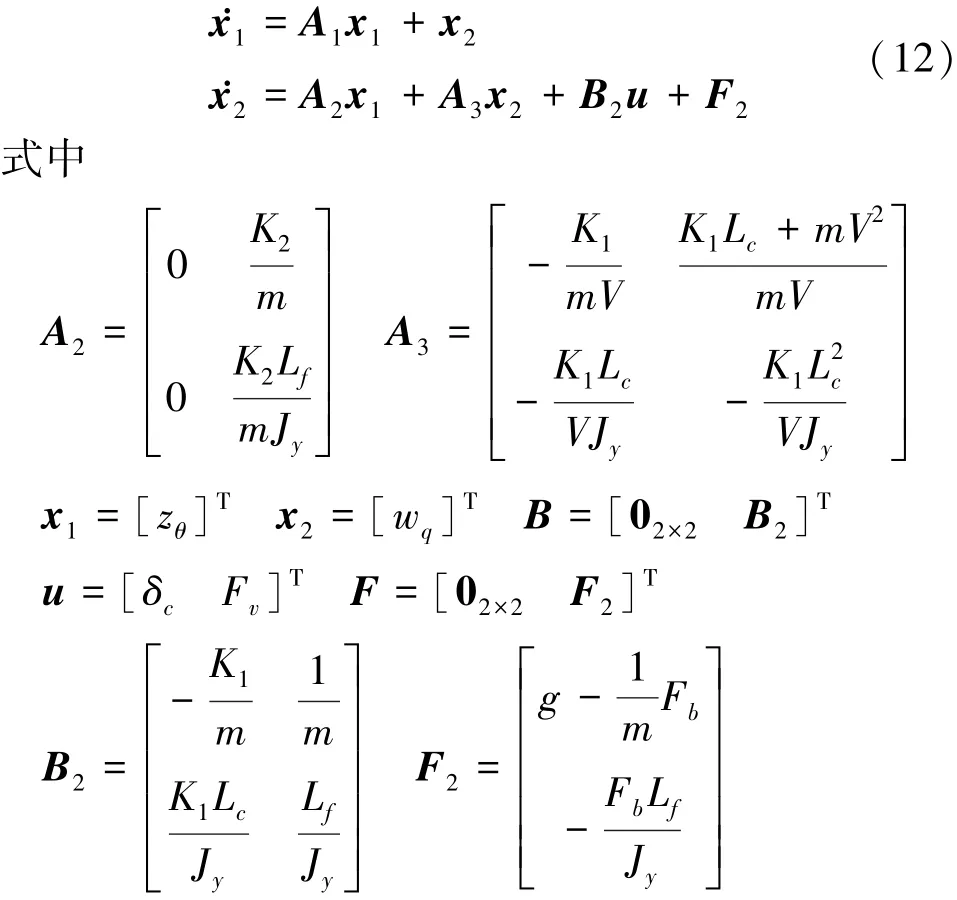
B2非奇异。

3.2控制器设计

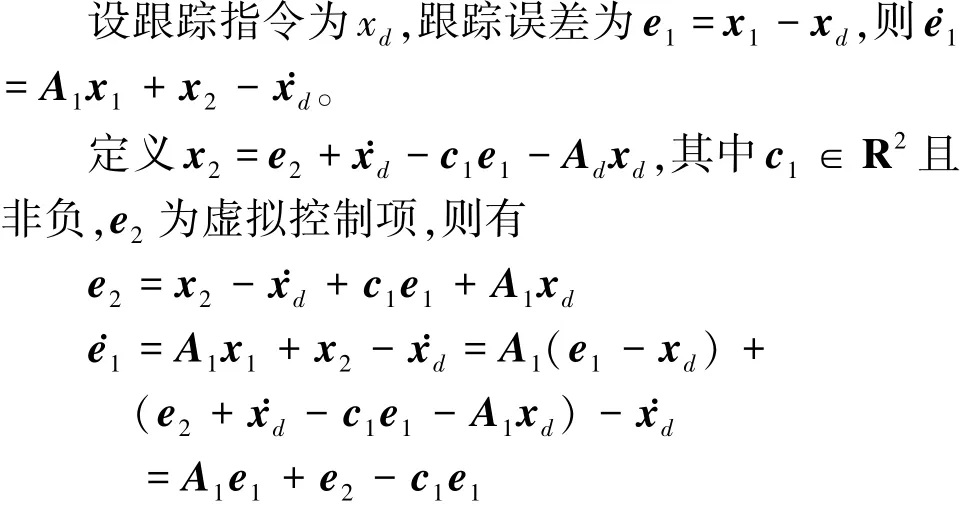
定义一个Lyapunov函数

对V1求导，则有

令c1＝A1，由A1各项元素可知，c1满足非负条件，则上式可进一步化简为

利用反演思想，设计线性切换面函数

式中，H为滑动模态参数矩阵，且正定。

根据非全包裹超空泡航行体纵向动力学模型可知，只要设计参数使z→0，θ→0，必能保证w→0，q→0，于是有

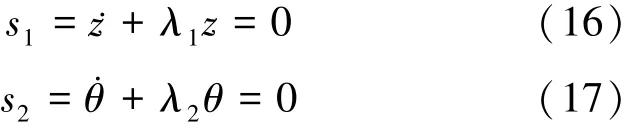
式中，λ1，λ2是保证(16)式、(17)式是Hurwitz的设计参数［10］。综合(15)～(17)式可进一步得到

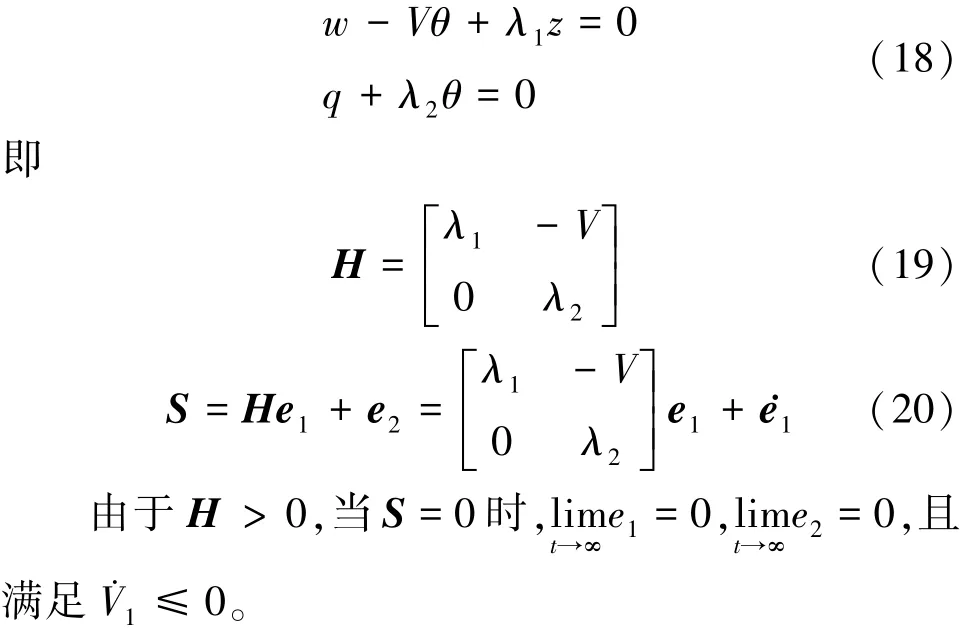
定义第二个Lyapunov函数

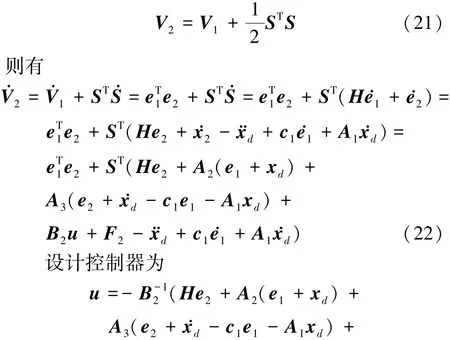
式中，h∈R，β∈R且h＞0，β＞0。

将控制输入u代入V2中可得

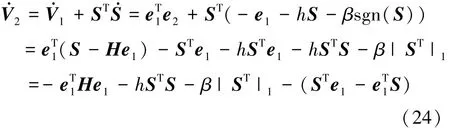
式中，｜ST｜1表示为ST的1范数，且由误差项e1和切换面函数S维数可知：STe1＝eT1S，因此，上式可整理成

由系统模型(12)可知，参数不随时间变化，该系统为自治系统，要使V.2＝0成立，当且仅当e1＝e2＝0成立，由LaSalle不变集定理，V2满足李雅普诺夫定理，系统渐进稳定。由以上推导可知，各个状态变量在闭环系统基于反演变结构控制器可实现跟踪控制。

由于控制律(23)是不连续函数，为防止出现抖阵现象，用sat函数代替sgn函数［18］，即

式中，ϕ＝0.1，s∈R。

4　仿真分析

为验证本文所设计的反演变结构控制器的有效性，对非全包裹超空泡航行体进行跟踪控制研究。跟踪控制的仿真验证主要分两部分，第一部分是深度z及俯仰角θ均为恒值的定深跟踪控制，第二部分将深度z的设定信号设置为正弦曲线，考虑验证控制算法的正弦跟踪控制效果，设计控制参数为h＝5，β＝0.01，λ1＝λ2＝1。

4.1定深跟踪控制

设定的航行深度为45 m，深度初始值为30 m，俯仰角设定值为0 rad，初始值为0.1 rad，并与单一变结构策略控制效果进行比较，如图3至图5所示。

由图3和图4可知，在控制输入(23)的作用下，各状态变量均能快速收敛。与单一变结构控制相比，反演变结构控制在各状态量及误差等方面的超调量较小，所引起的波动也更小，虽然初始阶段的响应速度稍慢于变结构控制，但两者各状态量收敛到稳定值的时间是相同的。图5表示系统状态变量的跟踪误差，可以看出，反演变结构的误差超调要小于变结构控制，反演变结构控制下的系统性能更优。

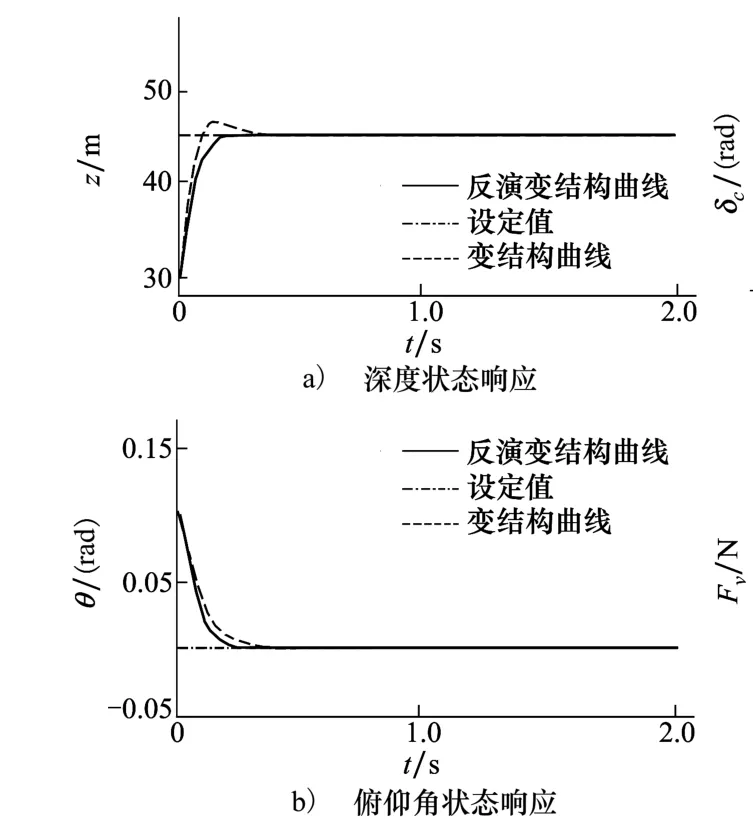
图3　定值跟踪控制状态响应

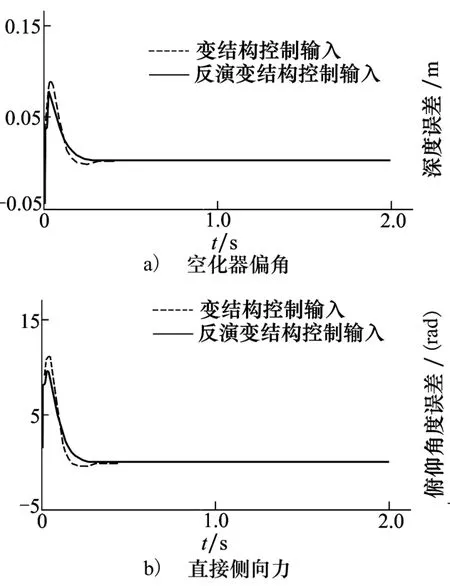
图4　定值跟踪控制输入

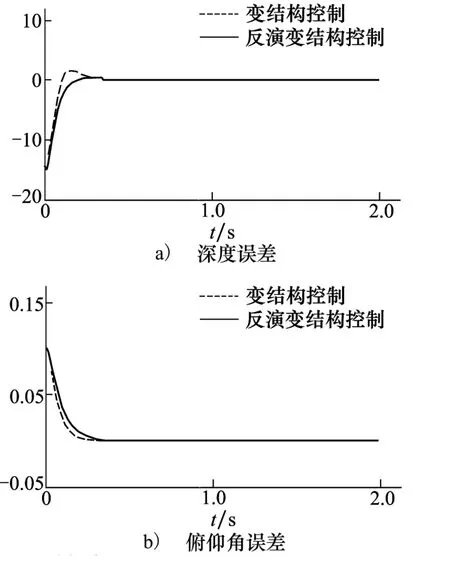
图5　定值跟踪控制误差曲线

4.2正弦跟踪控制

考虑如下的跟踪控制信号：设定的深度值为正弦曲线，根据(27)式将俯仰角设为关于深度设定值一阶偏导的函数［3］。仿真结果如图6至图8所示。

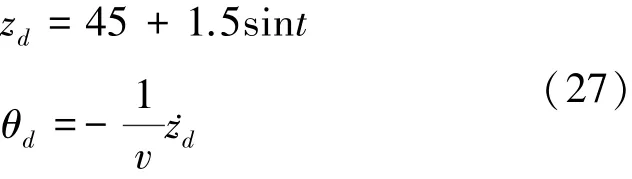
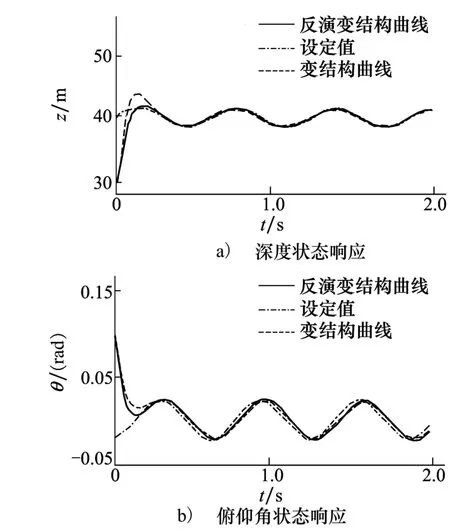
图6　正弦跟踪控制状态响应

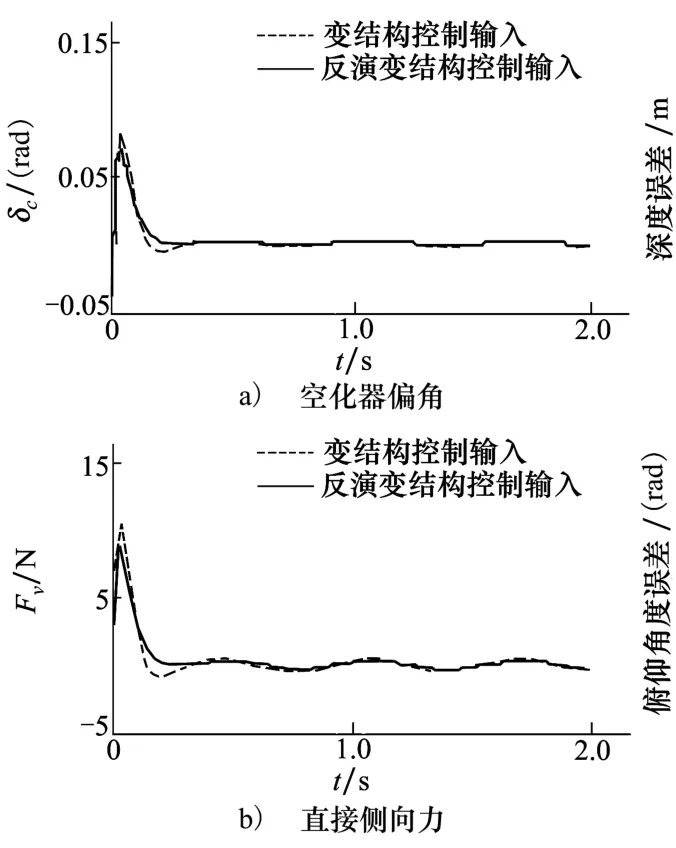
图7　正弦跟踪控制输入

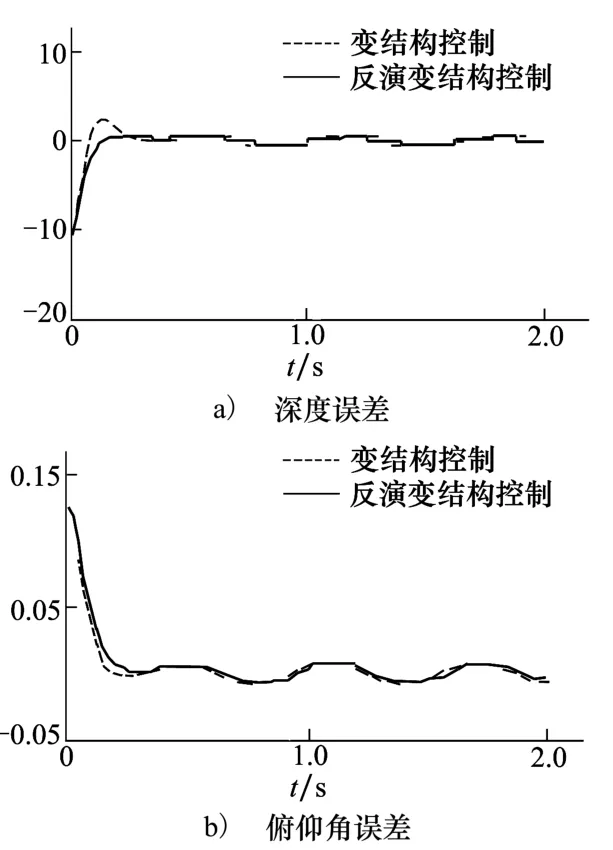
图8　正弦跟踪控制误差曲线

图6表示的是在正弦信号设定下的系统各参量响应曲线，可以看出，深度z及俯仰角都能够很好跟踪设定曲线，并且通过调整变结构控制中趋近律参数进一步削弱抖振。反演变结构与单一变结构在正弦跟踪控制效果上的区别与定值跟踪控制效果区别类似，与变结构控制方法相比，反演变结构的超调量更小，跟踪误差更快收敛到零。图7表示的是控制输入的曲线，明显可以看出两者虽然同时收敛，但反演变结构方法的2个控制输入均小于单一变结构方法，波动也更小。图8反映了类似的现象，单一变结构的超调较大，容易产生抖动，造成累积误差较大。

综上仿真结果不难看出，本文针对非全包裹超空泡航行体所设计的反演变结构控制器具有良好的控制效果，具有超调量小，抑制抖动，调节时间短，作用下的系统性能更优等特点。

5　结 论

本文针对非全包裹超空泡航行体的控制问题，构建了非全包裹超空泡的动力学模型，并据此设计了反演变结构控制器。通过分别对定值跟踪及正弦跟踪控制仿真分析证明，该控制器具有较好的控制效果，且与单一变结构控制器相比，其超调量更小，收敛速度更快。研究内容可用于超空泡航行体及类似复合控制航行体的姿轨控制问题。

［1］ Vanek B，Bokor J，Balas G J，et al.Longitudinal Motioncontrol of a High-Speed Supercavitation Vehicle［J］.Journal of Vibration and Control，2007，13(2)：159-184

［2］ Dzielski J E.Longitudinal Stability of a Supercavitating Vehicle［J］.IEEE Journal of Oceanic Engineering，2011，36(4)：562-570

［3］ Mao X，Wang Q.Adaptive Control Design for a Supercavitating Vehicle Model Based on Fin Force Parameter Estimation［J］. Journal of Vibration and Control，2013，1：2-4

［4］ Kirschner I N，Kring D C，Stokes A W，et al.Control Strategies for Supercavitating Vehicles［J］.Journal of Vibration and Control，2002，8(2)：219-242

［5］ Yu K，Zhang G，Zhou J，et al.Numerical Study of the Pitching Motions of Supercavitating Vehicles［J］.Journal of Hydrodynamics，Ser B，2012，24(6)：951-958

［6］ Kirschner I N，Uhlman J S，Perkins J B.Overview of High-Speed Supercavitating Vehicle Control［C］//Proceedings of the AIAA Guidance，Navigation，and Control Conference and Exhibit，2006：3100-3116

［7］ Li D，Luo K，Huang C，et al.Dynamics Model and Control of High-Speed Supercavitating Vehicles Incorporated with Time-Delay［J］.International Journal of Nonlinear Sciences and Numerical Simulation，2014，15(3)：221-230

［8］ Mokhtarzadeh H，Balas G，Arndt R.Effect of Cavitator on Supercavitating Vehicle Dynamics［J］.IEEE Journal of Oceanic Engineering，2012，37(2)：156-165

［9］ Kim S，Kim N.Neural Network-Based Adaptive Control for a Supercavitating Vehicle in Transition Phase［J］.Journal of Marine Science and Technology，2015，20(3)：454-466

［10］Vanek B，Balas G J，Arndt R E A.Linear，Parameter-Varying Control of a Supercavitating Vehicle［J］.Control Engineering Practice，2010，18(9)：1003-1012

［11］Qu Y B，Zhang J Y，Wu Y，et al.An Improved Sliding-Backstepping Control Law for Large Flexible Satellite Attitude Maneuver［C］//2010 3rd International Symposium on Systems and Control in Aeronautics and Astronautics，2010：918-923

［12］Mao X，Wang Q.Nonlinear Control Design for a Supercavitating Vehicle［J］.IEEE Trans on Control Systems Technology，2009， 17(4)：816-832

［13］Mao X，Wang Q.Delay-Dependent Control Design for a Time-Delay Supercavitating Vehicle Model［J］.Journal of Vibration and Control，2011，17(3)：431-448

［14］Vanek B，Bokor J，Balas G.Theoretical Aspects of High-Speed Supercavitation Vehicle Control［C］//American Control Conference IEEE，2006：5263-5267

［15］Kirschner I N，Rosenthal B J，Uhlman J S.Simplified Dynamical Systems Analysis of Supercavitating High-Speed Bodies［C］//Proceedings of the 5th International Symposium on Cavitation，2003：1-4

［16］Xia Y，Lu K，Zhu Z，et al.Adaptive Back-Stepping Sliding Mode Attitude Control of Missile Systems［J］.International Journal of Robust and Nonlinear Control，2013，23(15)：1699-1717

Modeling and BackstePPing Variable Structure Control for a IncomPlete-EncaPsulated SuPercavitating Vehicle

Li Yang，Lui Mingyong，Zhang Xiaojian，Peng Xingguang
(College of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China)

The special navigation environment of supercavitating vehicle causes it to be sensitive to disturbance and the dynamics system is highly nonlinear with multivariable coupling；these make it very difficult to design the control system.According to this problem，we study the control system for an incomplete-encapsulated supercavitating vehicle，design backstepping variable structure controller based on force analysis，establish the dynamic model， and prove the system stability.Numerical simulations illustrate the effectiveness of the proposed control method.

angular velocity，backstepping，cavitation，closed loop control systems，computer simulation，controllers，design，dynamics，efficiency，errors，Lyapunov function，mathematical models，matrix algebra， navigation，stability，variable structure control；incomplete-encapsulated，supercavitating vehicle， backstepping variable structure control

TP273

A

1000-2758(2016)02-0215-07

2015-10-20基金项目：国家自然科学基金(51379176、61473233、51109179)资助

李洋(1987—)，西北工业大学博士研究生，主要从事超空泡航行体姿轨控制研究。