关节臂式坐标测量机空间误差建模

陆 艺,张培培,王 华,王学影,赵晨馨

(中国计量学院 计量测试工程学院，杭州 310018)

关节臂式坐标测量机空间误差建模

陆 艺,张培培,王 华,王学影,赵晨馨

(中国计量学院 计量测试工程学院，杭州 310018)

关节臂式坐标测量机误差源多且复杂，其测量空间的误差存在不确定性，为了准确快速的得到关节臂式坐标测量机测量空间中的误差，利用标准锥窝对关节臂式坐标测量机进行了空间单点测量精度实验，获得了训练样本和测试样本;利用BP神经网络对空间误差进行了建模，为了提高其收敛速度和运算速度，引入粒子群优化算法(PSO)对BP神经网络模型进行了优化，并对模型进行了预测和验证;结果表明，BP神经网络和PSO-BP神经网络都可以对关节臂式坐标测量机进行空间点误差预测，PSO-BP神经网络模型的预测结果更加精确，相对误差更小。

关节臂式坐标测量机;空间误差;BP神经网络;PSO-BP神经网络

0 引言

关节臂式坐标测量机是一种多自由度的非笛卡尔式坐标测量机，它具有机械结构简单、造价低、测量范围大以及可移到现场测量等优点[1]，但由于其误差源较多且具有独特的多级串联式结构，导致在测量的过程中，误差会逐级增大，最终得到的测量结果精度偏低。因此建立关节臂式坐标测量机的空间误差分布模型，预测空间测量点误差，在实际的测量过程中，可以评定所测点的精度，亦可有效的避开精度较低的区域，具有实际的指导意义，是精密测量中的一个重要问题。西班牙学者Jorge Santolaria等人从温度角度出发，建立了关节臂式坐标测量机的热误差模型[2]；合肥工业大学汪平平运用微小位移法建立了关节臂式坐标测量机误差模型[3]；合肥工业大学博士郑大腾用泛函网络基本理论建立了关节臂式坐标测量机空间点误差模型[4]。国内外学者对空间误差分布模型的研究较少，首先利用标准锥窝对关节臂式坐标测量机进行了单点精度测量实验，获得训练样本以及测试样本，利用神经网络建模方式建立了关节臂式坐标测量机的空间误差分布模型，用测试样本验证了模型的有效性。

1 关节臂式坐标测量机的空间误差分析

1.1 关节臂式坐标测量机的误差来源

关节臂式坐标测量机的误差源多且复杂，很难进行系统的分析与研究，最终在测量空间中的误差是所有误差源的总和，根据研究，目前关节臂式坐标测量机误差来源主要有以下几种[5]：

1)角度传感器误差；2)结构参数误差；3)热变形误差;4)力变形误差;5)运动误差;6)数据采集系统误差;7)测头系统误差;8)测量方法不当、测量环境不合适造成的测量误差。

关节臂式坐标测量机在测量空间中进行测量时，上述1)～8)项误差源对空间中的每个点都存在影响且影响程度显而易见都是不同的[5]，导致其空间误差的大小也是不同的，研究空间误差分布可以更好地为关节臂式坐标测量机的精密测量提供理论基础。

1.2 关节臂式坐标测量机空间单点测量精度的评定标准及实验

根据文献美国国家标准的做法，利用标准锥窝对关节臂式坐标测量机空间单点测量精度的评定标准如下:

1)将标准锥窝置于关节臂式坐标测量机的测量空间中，测量机的触发式测头按照一定的要求探测该锥窝，获取该点n个采样数据Pi(Xi,Yi,Zi)，i=1,2,…n；

2)计算该n个采样数据的平均坐标Pa即((X, (Y, (Z)为该锥窝的真实位置；

3)计算该点n个采样数据Pi相对平均坐标点Pa的标准偏差σi；

(1)

4)以不确定度2S标准来评定其测量误差；

(2)

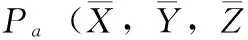
将标准锥窝置于空间中的点进行精度测量时，每个点位置重复测量了n=100组6个关节变量数据，这100组6个关节变量数据的获得是尽可能包含了所有位姿的组合以及探测的不同方向，这样所得到点的坐标发散程度就可反映出测量机的单点重复性，可以更好地评定测量误差。

将标准锥窝置于的位置最好能够均匀分布在整个测量空间上,这样可以更好的得到关节臂式坐标测量机整个测量空间误差分布。实验开始之前，先把关节臂式坐标测量机的测量空间按照球体划分为八个小区域，这八个小区域在每个小区域均匀的测得100组实验数据，共获得800组采样数据，这800组数据随机抽取700组数据作为训练样本，另外100组数据作为测试样本，用来验证模型的可靠性。

2 基于PSO-BP神经网络的空间误差模型建立

2.1 BP神经网络模型的建立

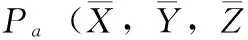
2.2 PSO-BP神经网络模型

BP神经网络是目前采用最多和最成熟的神经网络训练算法之一，但由于它采用非线性规划中的最速下降方法，按误差函数的负梯度方向修改权值，所以通常存在学习效率低，收敛速度慢以及易陷入局部极小状态的缺点[6]。而粒子群优化算法具有收敛速度快、全局搜索能力强的特点，用粒子群算法优化BP神经网络的初始权值和阈值，可以弥补BP神经网络的缺陷，有效提高神经网络的收敛速度和运算速度。

基本粒子群优化算法的数学描述如下[7]：

在D维搜索空间中，一个群体包含N个粒子，记作X=[x1,…,xN],粒子i的位置变化率(速度)记作vi=[vi1,…,viD]T,其位置记作xi=[xi1,…xiD]T,其中i=1,2,…,N;粒子i到当前迭代为止自身发现的最优位置记作pi=[pi1,…piD]T,到当前迭代为止全部粒子发现的最优位置记作pg=[pg1,…pgD]T，在找到这两个值之后，粒子通过下列公式进行更新[9]：

(3)

式中，i=1,2,…,N,d=1,…,D;c1,c2为学习因子，是非负常数，一般设为2；r1,r2是在[0,1]内的随机数；vid(t),xid(t)分别是粒子i当前的速度与位置；pid是粒子i发现的个体最优位置；pgd是粒子i发现的全局最优位置。

PSO-BP网络的训练步骤如图1所示。

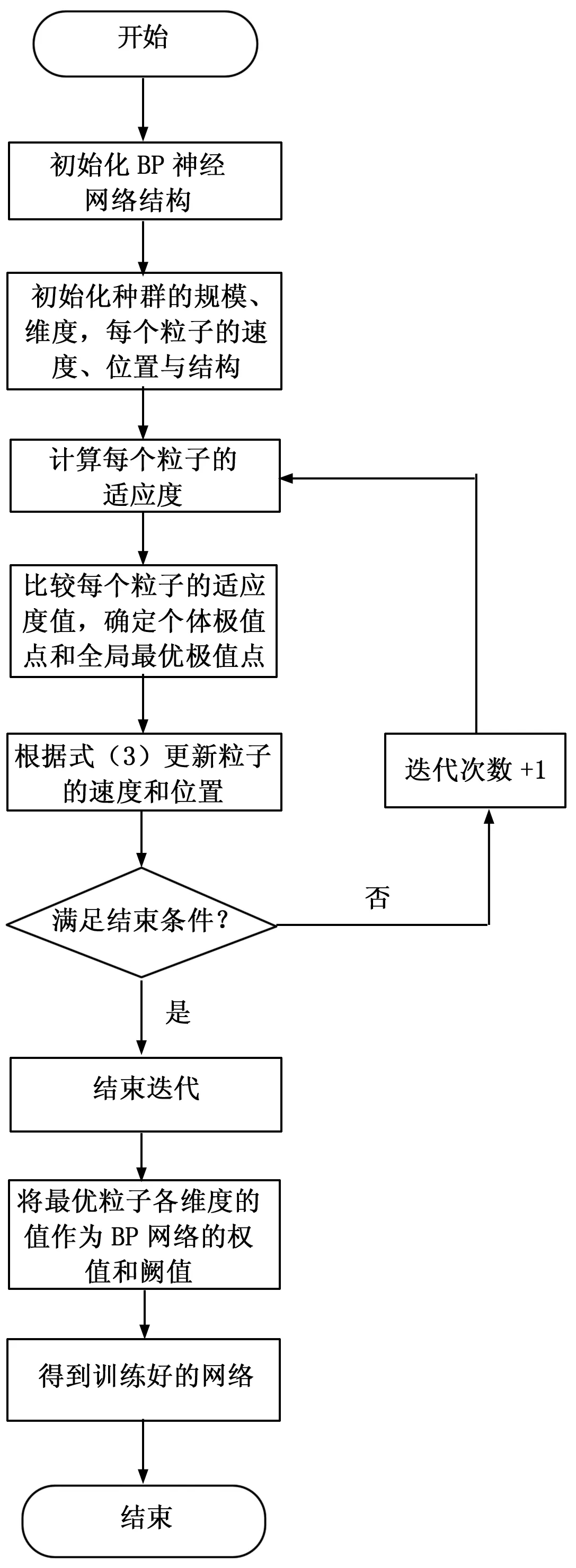
图1 PSO-BP网络的训练步骤

预测模型的参数的确定：

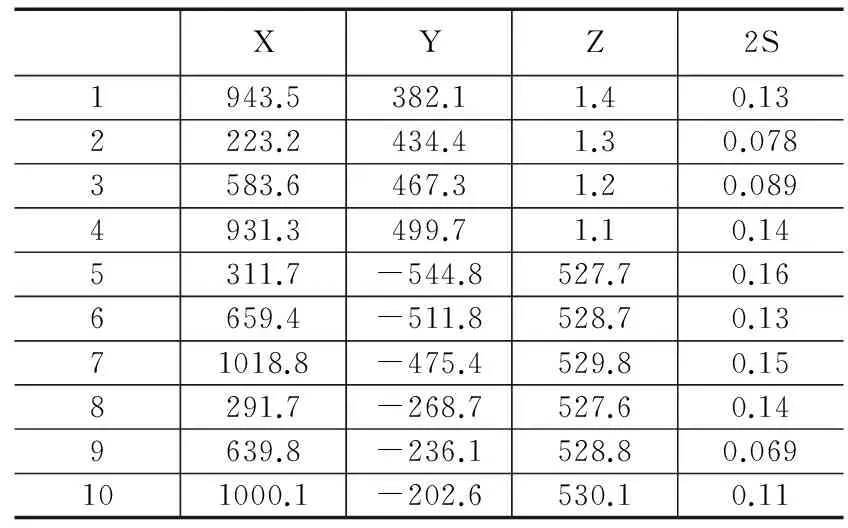
表1 训练样本数据表

3 PSO-BP神经网络空间误差建模

3.1 BP和PSO-BP神经网络模型分析

将测得的800组实验数据的其中700组数据用于对BP神经网络和PSO-BP神经网络的训练，后100组实验数据用于验证预测网络的可靠性,图2所示分别为BP神经网络和PSO-BP神经网络预测模型计算到50步的收敛曲线,横坐标为训练次数,纵坐标为训练误差。由图2可见两种神经网络的收敛曲线都一直呈下降趋势，但PSO-BP神经网络的收敛速度和运算速度都优于BP神经网络。图3是网络的预测结果比较图，其中图3(a)中横坐标是测点个数,纵坐标是关节臂式坐标测量机的点空间误差,可以看出两种网络建模均能有效预测出关节臂式坐标测量机的空间误差分布真实情况，图3(b)为BP网络和PSO-BP网络的预测结果相对误差曲线,可以看出经优化过的BP网络的预测误差明显小于未优化过的,即空间误差模型的预测精度得到提高。

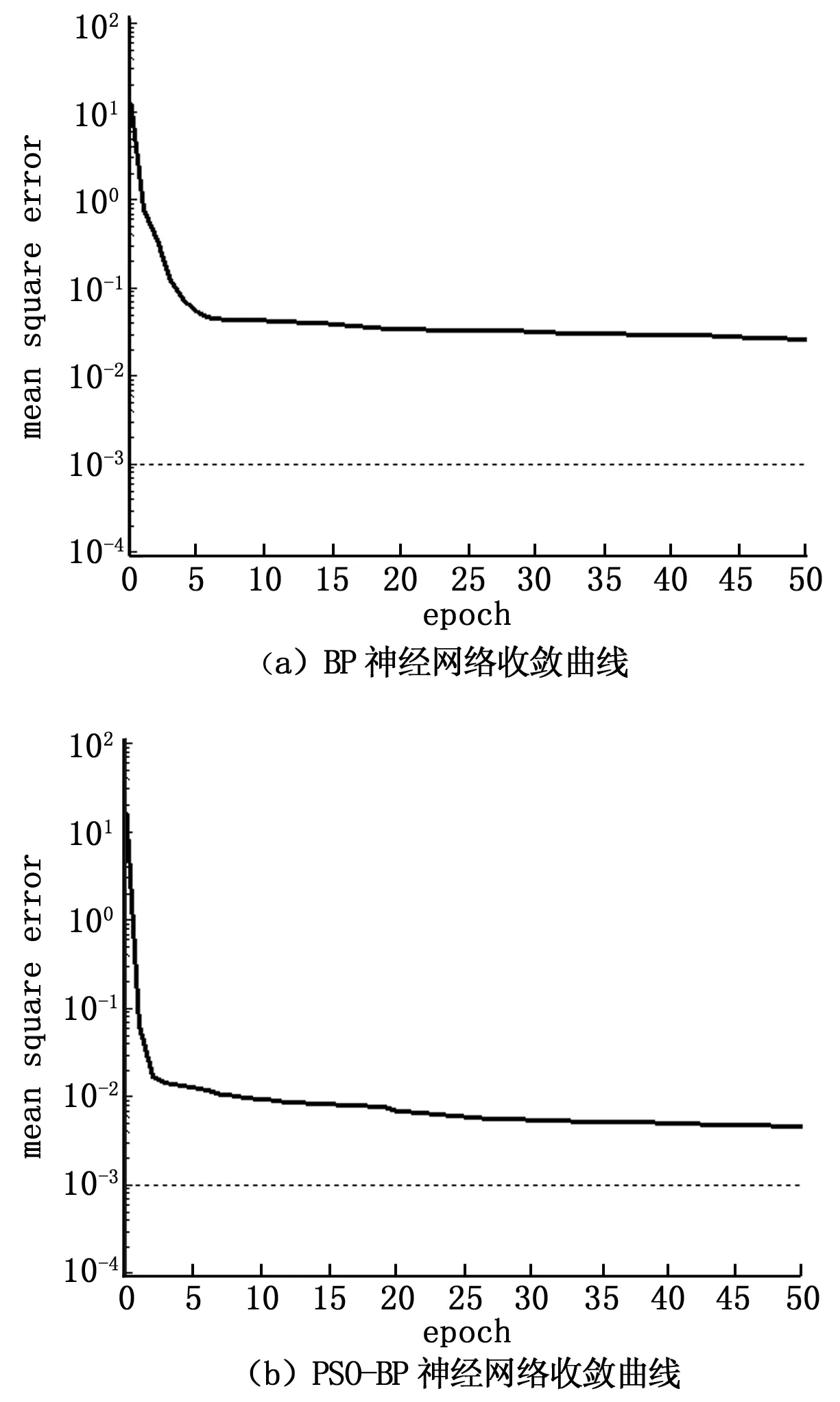
图2 BP和PSO-BP神经网络收敛曲线比较图

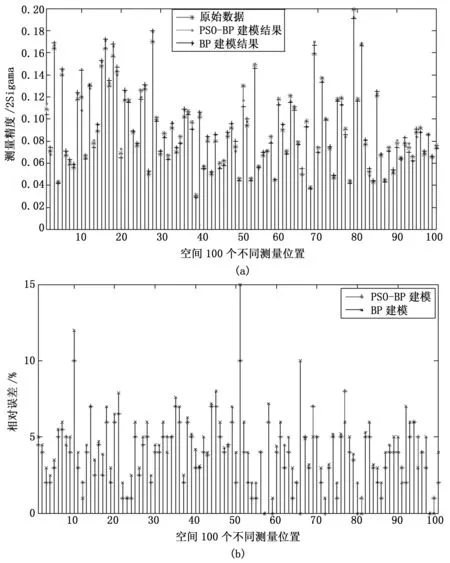
图3 BP和PSO-BP神经网络预测结果比较图

为了对BP神经网络和PSO-BP神经网络的预测效果进行对比,另外还采用均方根相对误差eMSE作为判断的依据,即[8]:

(4)

式中，A(i)和F(i)分别表示实测值和预测值果;n表示空间测量点数。

通过对BP神经网络和PSO-BP神经网络两种建模方法进行系统的分析，如表2所示。

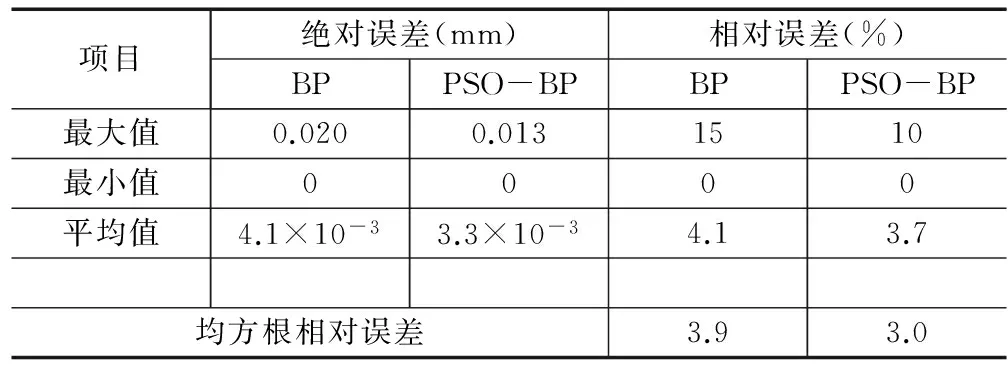
表2 BP网络与PSO-BP网络的预测值比较

由上分析可得，BP神经网络以及PSO-BP神经网络都可以对关节臂式坐标测量机的空间进行准确的预测，其预测的最大的相对误差均小于15%，平均相对误差以及均方根相对误差均小于5%，经过PSO优化的BP神经网络不仅提高了其收敛速度和运算速度，预测精度也有了很大的提高。

3.2 关节臂式坐标测量机空间误差分布

为了得到关节臂式坐标测量机的空间误差分布，在划分的关节臂式坐标测量机的8个小区域内，均匀的取3 000个点，利用PSO-BP神经网络预测其误差值，用软件MATLAB绘制出其测量空间误差分布。其空间误差分布截面图如图4所示，图4(a)为Z=0 mm，XOY截面半径R=1 200 mm时的误差分布图，图4(b)为Z=600 mm,XOY截面半径R=1 000 mm时的误差分布图，图4(c)为Z=1 000 mm,XOY截面半径R=600 mm时的误差分布图;图4(d)Y=600 mm，XOZ截面半径R=1 000 mm时的误差分布图，图4(e)为Y=1 000 mm，XOZ截面半径R=600 mm时的误差分布图;YOZ的空间误差分布和XOZ是相似的。

图4(a)、(b)、(c)分别为Z=0 mm,Z=600 mm以及Z=1 000 mm时XOY误差分布图，由此可得，误差在越靠近关节臂式坐标测量机测量空间边缘时，误差越大，在接近测量区域中间范围时误差相较较小。图4(d)、(e)分别为Y=600 mm,Y=1 000 mm时XOZ误差分布图，同理可得上面结论。

上述对关节臂式坐标测量机的空间误差分布进行了大致的分析与研究，但具体的最佳测量区域还有待于探索。

4 结论

由于关节臂式坐标测量机受其误差源的影响，测量空间的误差是存在不确定性的，利用BP神经网络模型对其空间误差分布建模，并引入粒子群优化优化BP神经网络的初始权值和

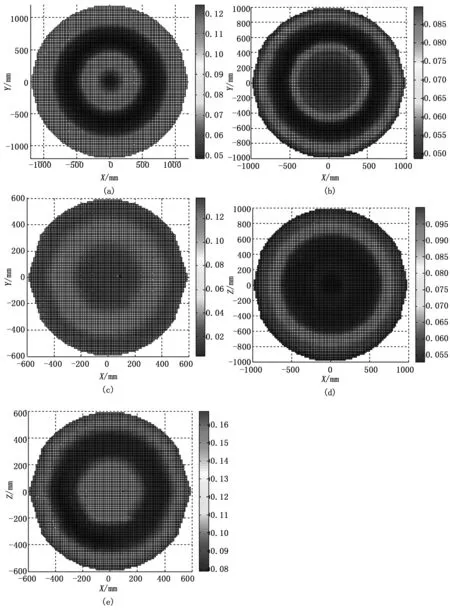
图4 关节臂式坐标测量机空间误差分布

阈值，提高其收敛速度和运算速度，实验证明：BP神经网络和PSO-BP神经网络都可以对关节臂式坐标测量机的空间误差进行预测，PSO-BP神经网络模型预测精度更高，具有理想的可靠性，并利用PSO-BP神经网络对对关节臂式坐标测量机的空间误差进行预测，用MATLAB绘制出其空间误差分布，在其测量空间范围内得出其误差分布的规律，在实际的测量应用中，可以避开其测量精度较小，误差较大的区域，具有现实指导作用。

[1] 裘祖荣, 孙增玉, 张国雄. 关节臂式坐标测量机标定系统的设计[J]. 计算机测量与控制, 2009, 17(1):88-90.

[2] Santolaria J, Yagüe J A, Jiménez R, et al. Calibration-based thermal error model for articulated arm coordinate measuring machines[J]. Precision Engineering, 2009, 33(4):476-485.

[3] 汪平平，费业泰，尚 平，等.柔性坐标测量机参数辨识方法[J].农业机械学报，2007，38(7)129-132.

[4] 郑大腾. 柔性坐标测量机空间误差模型及最佳测量区研究[D].合肥：合肥工业大学，2010.

[5] 高贯斌, 王 文, 林 铿,等. 关节臂式坐标测量机误差仿真系统建模与分析[J]. 计算机集成制造系统, 2009, 15(8):1534-1540.

[6] 何晓凤. 基于PSO—BP神经网络的混凝土抗压强度预测[J]. 微型机与应用, 2011, 30(20):87-90.

[7] 李 敏. 基于粒子群优化神经网络的刀具磨损状态监测技术研究[D]. 成都：西南交通大学, 2012.

[8] 王 亮, 张宏伟, 岳 琳,等. PSO-BP模型在城市用水量短期预测中的应用[J]. 系统工程理论与实践, 2007, 27(9):165-170.

Measurement Space Error Modeling of AACMM

Lu Yi，Zhang Peipei，Wang Hua，Wang Xueying，Zhao Chenxin

(College of Metrology & Measurement Engineering, China Jiliang University, Hangzhou 310018, China)

The error sources of AACMM were many and complex, and the measurement space error was uncertain.In order to obtain the measurement space error of AACMM accurately, the standard cone was measured on AACMM, and also obtain the training data sample and test data sample, the AACMM’s measurement space error model was built up by BP neural network,and the particle swarm optimization algorithm (PSO) was introduced to optimize the convergence speed and the operation speed of BP neural network, and the prediction and verification of the model was carried out. Results show that BP neural network and PSO-BP neural network both can predict the measurement space error,the prediction results of PSO-BP neural network model are more accurate, and the relative error is smaller.

AACMM;Space error; BP neural network; PSO-BP neural network

2016-04-18；

2016-05-19。

国家自然科学基金资助项目(51405463);杭州式汽车零部件智能检测科技创新服务平台(20151433S01)。

陆 艺(1979-)，男，江苏扬州人，副教授，硕士研究生导师，主要从事精密测试方向研究。

1671-4598(2016)07-0291-03

10.16526/j.cnki.11-4762/tp.2016.07.078

TH721 文献标识码：A