不同时间尺度下锂电池SoC估算研究

潘海鸿，李君子，吕治强，林伟龙，陈 琳

(广西大学 机械工程学院，南宁 530000)

不同时间尺度下锂电池SoC估算研究

潘海鸿，李君子，吕治强，林伟龙，陈 琳

(广西大学 机械工程学院，南宁 530000)

针对当前电池荷电状态(SoC)估算算法在处理器运算过程中计算量大，耗费处理器资源多的问题，提出在SoC估算中同时增大辨识时间尺度和估算时间尺度；采用带遗忘因子递推最小二乘算法辨识电池模型参数，并探究不同大小的时间尺度对SoC估算精度的影响；仿真结果表明，随着辨识时间尺度和估算时间尺度增大，SoC估算精度下降且计算量快速下降，计算消耗时间呈指数减少；当时间尺度过大时，SoC估算精度难以保证，计算消耗时间减少不明显，收敛时间长；在综合考虑估算精度和计算耗费时间情况下，可以找到一个最优的时间尺度用于保证SoC估算精度同时大大降低计算量；该方法为后续实现电动汽车SoC在线估算提供理论依据。

锂离子电池；电池荷电状态；最小二乘法；

0 引言

近年来，环境污染和能源短缺带来的问题越发明显，如何解决这些问题一直是工业发展中的重中之重，电动汽车因其零排放，结构简单受到越来越多的关注。世界各国都在大力发展电动汽车技术，预计到2050年，在世界范围内电动汽车的市场占有率将达到60%[1-2]。锂离子电池具有寿命长，能量密度大、功率比高等特性[3-4]，是电动汽车主要动力来源。但在电动汽车运行过程中，复杂工况以及电池本身各自差异都对电池运行状态产生重大影响，因此作为连接动力电池和电动汽车的重要纽带，电池管理系统(BMS)必不可少[5]。电池荷电状态(SoC)是BMS中实时监控的一个重要参数，是电池管理核心技术之一，它能够评判电池剩余电量多少，它也是判断电池是否过充电或过放电的重要依据，是电动汽车安全可靠运行的重要保障。为了提高SoC估算精度，大量SoC估算方法被提出，现有常用方法大致可以分为两类：第一类将电池看作一个“黑箱”的模糊逻辑和机器学习类方法，第二类是基于等效电路模型和电化学模型方法。在第一类方法中，人工神经网络算法，模糊逻辑算法和支持向量机[6-8]等需要训练大量的数据，数据需求量和计算量大，难以应用于实际的BMS中。而第二类基于模型算法用电阻、电容等构成电路，模拟电池在不同工况下的放电特性，在其基础上提出有开路电压法，卡尔曼滤波器算法，PI观测器算法等[9-11]。在基于模型算法中准确辨识出电池模型的参数至关重要，一个正确电池模型才能实时反映出电池特性。确定电池模型参数后，依据电池模型可以实施电池SoC估算。电池模型参数辨识和电池SoC估算往往是在同一时间尺度实行，如双卡尔曼估算/联合扩展卡尔曼[12]等。但电池参数是一个较为缓慢变化的量，而电池状态如SoC具有快速时变特性。同一时间尺度下电池参数和状态估算如果都选取较小的时间尺度，将耗费大量计算资源。因此不同时间尺度下电池参数和电池状态估算被提出[13-14]，在这些文献中提出采用宏观时间尺度和微观时间尺度分别对应模型参数辨识时间尺度和电池状态更新时间尺度，在估算SoC时通过改变辨识时间尺度(宏观时间尺度)的大小减小计算成本提高估算精度，而状态估算时间尺度(微观尺度)选取较小的时间尺度来达到实时更新的效果，但在SoC估算中，较小的估算时间尺度带来的计算量大，消耗处理器资源多。考虑到SoC虽然是一个迅速变化量，在实际汽车应用中，驾驶员对SoC观察往往都是一个间断的不定时的量。适当降低SoC的更新频率符合驾驶习惯同时也能进一步减少计算量和占用的处理器资源。因此，在电池状态估算中，提出同时增大辨识时间尺度和估算时间尺度，基于电池Thevenin模型，采用带遗忘因子的最小二乘法(FFRLS)探究了在不同大小时间尺度对SoC的估算的影响。

1 锂离子电池建模

Thevenin等效电路即一阶RC模型，综合考虑到电池模型的精确度和复杂程度。Thevenin等效电路更适用于模拟锂离子电池的动态特性，电池模型具体如图1所示。

图1 Thevenin等效电路

图1中IL为电池所受激励电流(IL符号以电池放电时电流方向为正，以电池充电时电流方向为负)；Uoc表示锂离子电池开路电压部分，该部分常视为Uoc=f(SOC)；Ut为电池端电压；R0表示锂离子电池欧姆内阻部分；R1和C1分别为极化内阻和极化电容；

Thevenin模型等效电路方程表达式为(1)：

(1)

为后续辨识模型参数，将等效电路模型改写为离散化时间序列形式，方程式(1)可改写为(2)：

(2)

其中:k为采样序列时刻序号，k=1，2，3，…，n。

Thevenin等效电路模型中的参数R1,C1,R0可以从a1,a2,a3中推导得出，相关的计算关系式如(3)，(4)：

(3)

(4)

2 锂离子电池建模模型参数辨识

递推最小二乘算法的提出源于最小二乘算法并结合自适应滤波理论，是一种在锂离子模型参数辨识上经典算法。带遗忘因子的递推最小二乘是最小二乘算法的改进，在对采样序列中旧数据乘以一个给定的遗忘因子，将老数据对参数估算的影响权重降低，同时新信息对系统参数辨识影响程度较大，且保证数据越新权重越大。在使用算法做锂离子Thevenin模型参数辨识时，需先将系统数学表达式变换成如公式(5)所示：

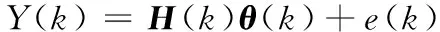
(5)

其中:e(k)为算法对电池端电压值预测误差，其中Y(k)为系统输出变量。系统数据矩阵H(k)与系统输出变量Y(k)均可以通过对电池进行数据采集和记录获得，通过求解方程组即可求出系统参数矩阵θ(k)，利用系统参数矩阵结果代入公式(4)计算得模型参数。

结合Thevenin等效电路模型，递推最小二乘法具体表达示为(6)：

(6)

FFRLS算法表达式(7)：

(7)

式(7)中，K(k)为算法增益矩阵在k时刻的值，P(k)为算法协方差矩阵在k时刻的值，θ(k)为算法估算的k时刻系统参数矩阵，λ为FFRLS遗忘因子系数，通常其取值范围在[0.95,1]区间内。特别的，当λ值为1时，FFRLS算法变成标准递推最小二乘算法。利用FFRLS算法进行1阶RC模型辨识时递推求解出每一时刻θ(k)值，即可计算1阶RC模型式(3)中的参数。

3 实验结果分析

3.1 实验平台

该实验平台由锂离子电池(18650-NMC)、一台直流电源、电子负载仪、恒温箱、中央控制电脑以及为搭建平台所必须的一些硬件辅助设备，如导线等。

实验开始前每组电池先以1.3A的恒定电流(CC)模式进行充电，直到电压达到4.2V；然后以一个恒定电压(CV)模式继续充电，直到充电电流下降到20mA。根据不同放电工况放电，截止电压为2.75V。

3.2 电池模型参数的验证

UDDS(urbandynamometerdrivingschedule)工况是一种典型的动态工况，选用UDDS工况(UrbanDynamometerDrivingSchedule)动态工况来验证带遗忘因子的最小二乘法辨识电池模型在动态工况下的精度，获得端电压试验结果与模型仿真结果及误差如图2所示端电压误差统计结果图2(b)所示，其平均误差0.6mV；误差标准差为0.0185。等效电路模型误差在1%以内，表明基于FFRLS辨识的Thevenin模型具有较高精度，能够真实模拟锂离子动力电池的动态特性。

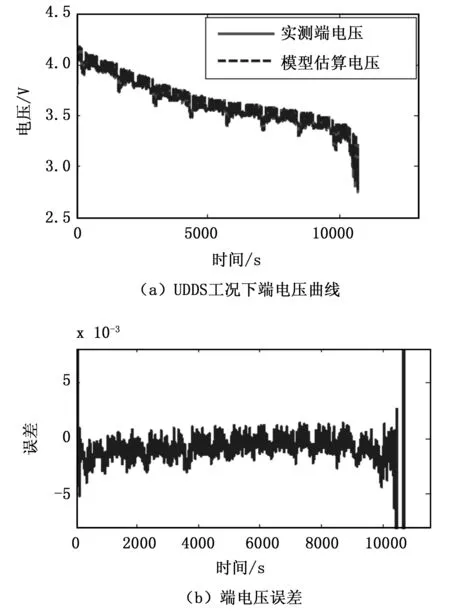
图2 USSD工况下端电压结果及误差

3.3 锂离子动力电池SoC估算

基于上述FFRLS辨识结果，可从参数矩阵(1-a1)UOC(K)计算出电池实时开路电压，依据开路电压与SoC关系Uoc=f(SOC)，通过查表法，可以估算电池SoC，其中Uoc=f(SOC)通过静置法放电发和插值获得相应的OCV-SoC关系。

3.4 不同时间尺度SoC估算结果

选用电池在UDDS工况下的放电结果，模型参数辨识时间尺度和SoC估算时间尺度设为同一时间尺度L，L从1秒至60秒逐渐增大，间隔为1秒。均匀选取时间尺度为L=5，20，35，50(s)下SoC的结果为代表反应不同时间尺度下SoC估算结果如图3所示。

图3 不同辨识时间尺度下SoC估算结果

不同时间尺度下对应的SoC平均误差和估算消耗时间如图4所示。

图4 不同时间尺度下SoC误差与估算消耗时间

从图3(a)～3(d)，可以看出，在不同时间尺度下SoC估算收敛时间随着时间尺度的增大而增大。FFRLS辨识模型参数需要一定收敛时间，随着时间尺度增大，在同一段时间内，辨识时间尺度大包含数据量少，需要更多时间才能达到收敛。辨识所用时间尺度小，同一时间所含包含数据量更多，则能更快达到收敛，但计算量大。因此过大时间尺度导致算法收敛性变差。从图4可知，在不同时间尺度下SoC精度呈现非线性变化。时间尺度在1～10s之间，SoC误差呈现近似线性增长，但当选择辨识参数时间尺度继续增大时(L>10)，SoC估算误差虽然有所下降但仍处于较大范围。较大时间尺度意味着在一段较长的时间内电池参数是固定的，相对于较小的时间尺度(如L<5)，虽然参数较为稳定但估算精度下降。从计算消耗时间来看(同一硬件处理器配置上，消耗时间少，计算量少，占用处理器资源少)，当时间尺度(L<10)，计算消耗时间随着时间尺度增大呈现指数衰减关系，当时间尺度(L>10)时，计算消耗时间随着时间尺度的增长衰减速度不明显而估算精度仍处于误差较大范围。从图3(a)～3(d)中也可以看出算法随着时间尺度增大，估算收敛时间增大。因此，综合考虑估算精度和计算成本，时间尺度选取应该在误差线和时间消耗线交点处(L=4)更合理，在这个范围内SoC估算精度虽然有所下降，但参数较为稳定，误差也在可接受范围，而计算量将大幅度减少，消耗处理器资源少。因此一个合适时间尺度不仅能跟踪电池特性变化，正确估算电池各项状态，同时也能够减少处理器计算量，释放处理器资源，更适用于电动汽车BMS状态计算监控等。

4 结论

针对电动车电池SoC算法在处理器运算过程中计算量大、消耗处理器资源多的问题，为进一步减少计算量，提出同时增大辨识时间尺度和估算时间尺度，建立并分析锂电池模型，辨识电池模型参数，在UDDS动态工况下验证了所使用的电池模型和辨识方法，探究了不同时间尺度下辨识和估算对SoC估算的精度影响，结果表明，时间尺度在1s～10s之间，SoC误差呈现近似线性增长而计算成本几何指数减少，即随着时间尺度增大，SoC精度下降但计算成本下降更快，而过大时间尺度，辨识结果不能够准确描述电池放电特性、估算结果误差增大、收敛时间长且计算成本减少不明显。因此综合考虑计算成本与估算精度，时间尺度选取4s能够很好的模拟电池工况同时也能大大减少运算量，更有利于SoC的在线估算。

[1]SunB,JiangJ,ZhengF,etal.PracticalstateofhealthestimationofpowerbatteriesbasedonDelphimethodandgreyrelationalgradeanalysis[J].JournalofPowerSources, 2015,282:146-157.

[2]BarréA,DeguilhemB,GrolleauS,etal.Areviewonlithium-ionbatteryageingmechanismsandestimationsforautomotiveapplications[J].JournalofPowerSources, 2013,241:680-689.

[3] 艾 力, 房红征, 于功敬, 樊焕贞. 基于数据驱动的卫星锂离子电池寿命预测方法[J]. 计算机测量与控制, 2015, 23(4):1262-1265.

[4] 宋绍剑, 林庆芳, 林小峰. 纯电动汽车磷酸铁锂电池组的建模及优化[J]. 计算机测量与控制, 2015, 23(5):1713-1716.

[5]XingY,MaEWM,TsuiKL,etal.BatteryManagementSystemsinElectricandHybridVehicles[J].Eenrgies, 2011,4(11):1840-1857.

[6] 尹安东, 张万兴, 赵 韩, 等. 基于神经网络的磷酸铁锂电池SOC预测研究[J]. 电子测量与仪器学报, 2011,25(5), 433-437.

[7] 于 洋, 纪世忠, 魏克新. 基于LS-SVM算法动力电池SOC估计方法的研究[J]. 电源技术, 2012, 36(3):349-351, 370.

[8] 石庆升. 纯电动汽车能量管理关键技术问题的研究[D]. 济南：山东大学, 2009.

[9]TongS,KleinMP,ParkJW.On-lineoptimizationofbatteryopencircuitvoltageforimprovedstate-of-chargeandstate-of-healthestimation[J].JournalofPowerSources, 2015,293:416-428.

[10]XuJ,MiCC,CaoB,etal.TheStateofChargeEstimationofLithium-IonBatteriesBasedonaProportional-IntegralObserver[J].VehicularTechnology,IEEETransactionson, 2014,63(4):1614-1621.

[11]JunpingW,JingangG,LeiD.AnadaptiveKalmanfilteringbasedStateofChargecombinedestimatorforelectricvehiclebatterypack[J].EnergyConversionandManagement, 2009,50(12):3182-3186.

[12]PlettGL.ExtendedKalmanfilteringforbatterymanagementsystemsofLiPB-basedHEVbatterypacks:Part1.Background[J].JournalofPowerSources, 2004,134(2):252-261.

[13]XiongR,SunF,ChenZ,etal.Adata-drivenmulti-scaleextendedKalmanfilteringbasedparameterandstateestimationapproachoflithium-ionolymerbatteryinelectricvehicles[J].AppliedEnergy, 2014,113(0):463-476.

[14]HuC,YounBD,ChungJ.AmultiscaleframeworkwithextendedKalmanfilterforlithium-ionbatterySoCandcapacityestimation[J].AppliedEnergy, 2012,92(0):694-704.

Research on Lithium-ion Battery State of Charge Estimation Under Different Time Scale

Pan Haihong, Li Junzi, Lü Zhiqiang, Lin Weilong, Chen Lin

(College of Mechanical Engineering, Guangxi University, Nanning 530000, China)

In order to solve the problem of heavy calculation burden and large consumption of microcontroller cost that faced in current algorithm of state of charge (SoC) estimation. Increasing time scale of estimation and parameters identification is proposed to estimate SoC. The recursive least squares algorithm with forgetting factor is used to identify battery model and estimate the SoC. The influence of different sizes of time scales for the accuracy of SoC estimation is explored. Simulation results show with the increase of identified time scale and estimated time scale, the accuracy of SoC decrease and calculation burden decline rapidly, the computing time present an exponential decay. An oversize time scale can't guarantee SoC estimation accuracy, the computing time is not decay obviously and the convergence time is long, Comprehensive consideration of estimation accuracy and computing time, an optimal time scale can be achieved which can reduce calculation burden, and ensure accuracy of SoC estimation. The method provides theory basis for subsequent implementation of online SoC estimation in electric vehicles.

lithium-ion battery; state of charge; least square method

2016-01-12；

2016-03-07。

国家自然科学基金(51267002);广西自然科学基金资助(2015GXNSFAA139287)。

潘海鸿(1966-)，男，广西南宁人，教授，博士研究生导师，主要从事高速高精度运动控制、数控技术、嵌入式控制系统和IC 装备方向的研究。

陈 琳(1973-)，女，山东青岛人，教授，硕士研究生导师，主要从事信号检测与处理方向的研究。

1671-4598(2016)07-0249-04

10.16526/j.cnki.11-4762/tp.2016.07.068

TN713 文献标识码：A