基于几何差异的目标识别算法
2016-10-28王彦芳邓秀剑
王彦芳, 冯 琦, 邓秀剑
(1.西北工业大学 电子信息学院, 西安 710072;2. 航空电子系统综合技术重点实验室, 上海 200233)
基于几何差异的目标识别算法
王彦芳1, 冯 琦1, 邓秀剑2
(1.西北工业大学 电子信息学院, 西安 710072;2. 航空电子系统综合技术重点实验室, 上海 200233)
为降低目标识别算法复杂性且提高其抗噪能力,提出一种基于几何特征差异的目标识别算法;将获取到的目标图片经图像处理后提取轮廓,并以最小周长多边形算法构造目标轮廓的近似多边形;然后根据模板库标准目标做放大或缩小处理后使其面积与模板面积相等;再使用摆放算法使其与模板库图形部分重合;并提出一种改进型双向链表算法求多边形相交部分,通过计算相交部分面积大小达到识别图像的目的;经过仿真实验验证了此方法简单易行,能够快速识别目标。
目标识别;多边形拟合;多边形相交面积;双向链表
0 引言
利用形状特征来描述物体并加以识别是复杂背景下目标自动识别技术的一个重要研究方向。传统的识别方法大都建立在对目标统计特征提取的基础之上,而这些统计特征是经过人为的处理变换才能得到,如文献[1]抽取图像轮廓,对曲率进行傅里叶变换来得到形状的特征向量,该方法形状区分能力强但是对噪声比较敏感;文献[2]提出一种基于最佳匹配点、利用交比来识别平面图形的方法,但是此方法容易因为个别点匹配位置错误而导致不能识别目标量;文献[3]提出一种基于k聚类分析法的目标识别算法,但是该方法精度不高,只能对具体数据进行分析而不能增加新的数据对象。
本文直接利用目标的几何形状这一原始几何特征,克服了统计特征识别目标处理复杂、易受噪声影响等缺点,通过目标多边形与模板库中多边形交面积大小达到识别目标的目的。仿真实验证明,该方法几何特征明显,简单高效,提高了识别的实时性。
1 图像预处理
在进行图像识别之前需要对图像做一些预处理,目的是对系统获取的原图像基本特征信息进行相应的、有针对性的处理,以滤除干扰噪声,突出下一步图像识别中所关注的边缘信息。其过程主要包括图像灰度化、图像平滑、图像滤波、图像增强、图像边缘检测以及多边形逼近。
图像灰度化是将彩色图像转换成灰度图像,以提高图像的处理速度;图像平滑是压制和削弱突变和噪声,一般采用邻域平均法[4];图像滤波主要采用中值滤波,可有效消除孤立噪声点干扰,而且能很好地保留图像边缘轮廓,有利于后续图像的识别;图像增强主要是改善图像视觉效果,有目的地强调图像整体或局部特性;图像边缘检测的目的是标识数字图像中变化明显的点,大幅度减少数据量,尽量只保留图像重要的结构属性;多边形逼近的目的是去除边缘轮廓中小区域的凹凸不平对待识别目标形状的影响,可采用最小周长多边形算法[5]得到目标轮廓近似多边形,达到简化识别目标主体轮廓并减少后续识别复杂度的目的。
通过以上图像预处理,就得到了待识别目标的轮廓多边形。
2 轮廓多边形的相关处理
2.1 相似性变换
实际中获取的轮廓多边形通常与模板库中的多边形大小不同,与其对应的标准图形轮廓多边形有相似的关系,所以在比较之前要对轮廓多边形做放大或缩小处理,使其面积与模板库中所进行比较的多边形面积一致,假设图1中多边形A表示获取的轮廓多边形,多边形B表示模板库中多边形,要将多边形A放大至与B面积相等,其具体步骤如下:
步骤 1:计算多边形A与多边形B的面积SA、SB。多边形A,B的相似比为k(B/A)。
步骤 2:从平面上任取一点O,连接该点与多边形A的各顶点,计算每条连线长度li(i=1,2,3,4,5),将其按远离O的方向延长(当k<1时在O与顶点连线上取点)使得Li=k*li,得到点B1、B2、B3、B4。
步骤 3:连接点B1、B2、B3、B4即得到放大(或缩小)后的多边形。
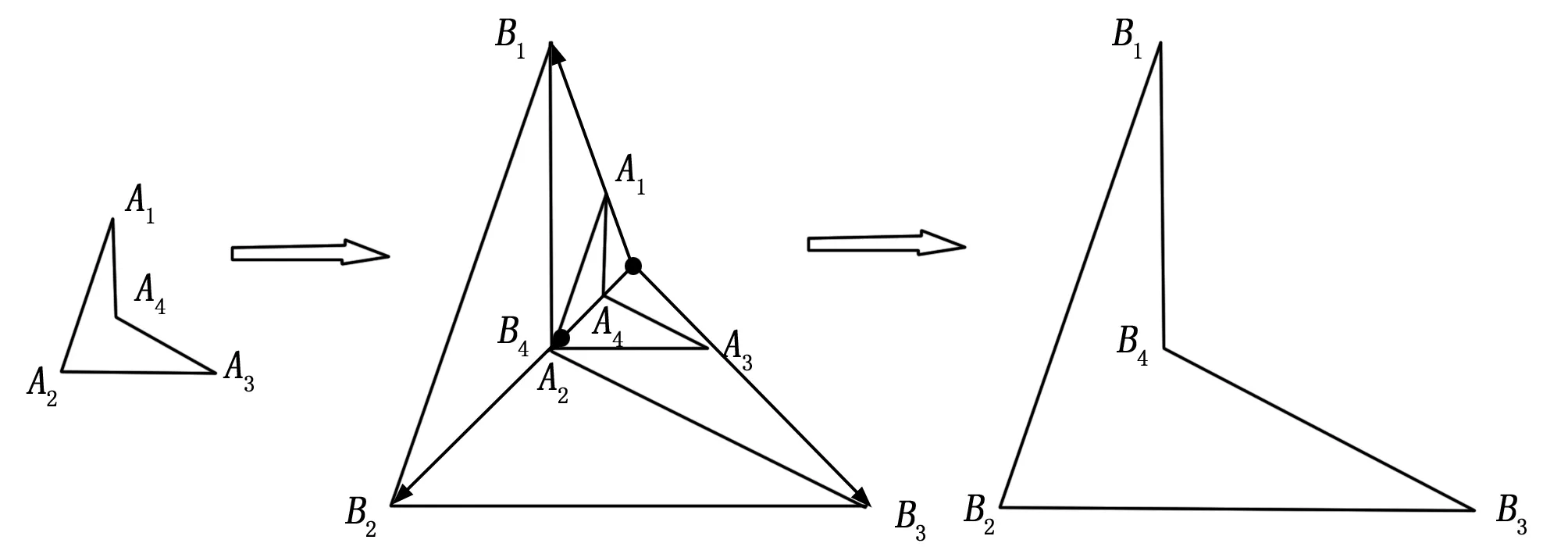
图1 多边形相似变换过程
2.2 多边形重叠方式选择
将进行放大或缩小后的轮廓多边形与模板库中的多边形一一重合以计算其相交面积。多边形重合方式有无数种,在识别时需要从中选择最合适的重合方式。显然当两个多边形面积相等时,相交面积越大,两个多边形相同的可能性越大。本节算法采用一种基于重心距离限定[6]的多边形摆放方式。算法流程如下。
输入:经过相似多边形处理后的多边形A的顶点坐标Ai(i=1,2,…,n),模板库多边形B的顶点坐标Bj(j=1,2,…,k)(n、k表示多边形的顶点个数)。
输出:调整摆放位置后的多边形。
步骤 1:计算多边形A的重心OA以及多边形B的重心坐标OB。
步骤 2:对多边形A,B做如下处理:
多边形A做旋转平移处理得到Ai,j,使得A第j条边与B的第i条边重叠且中点重合;
计算这种摆放方式下的重心距离di,j;
设置重心阈值d*;
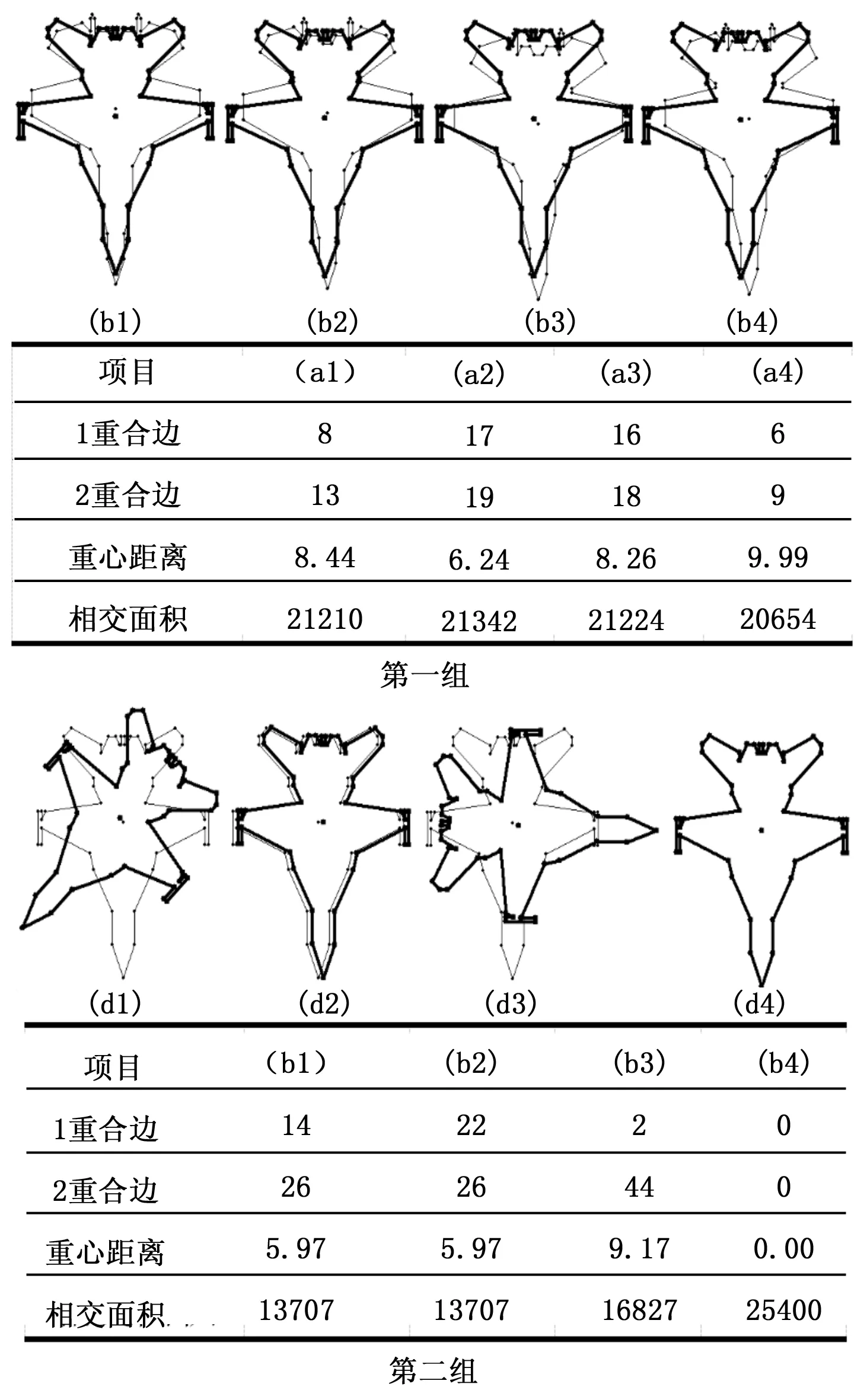
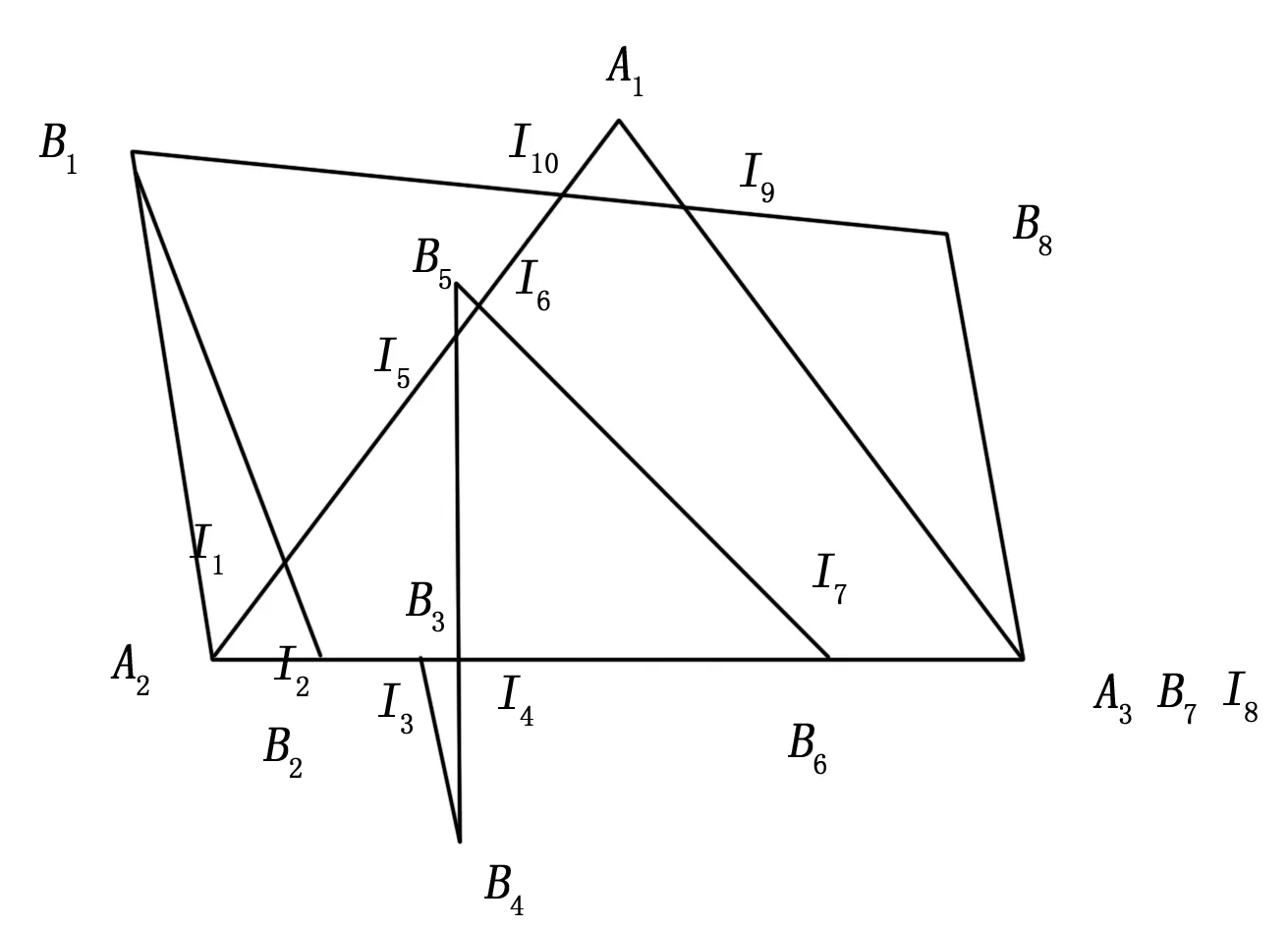
If(di,j 从几何知识可以知道,当i=p,j=q时,若相交面积达到最大值,dp,q将相应地较小。相反,若dr,s比较大,那么相交面积将较小,如图2。 图2 多边形摆放方式选择 用集合Г表示多边形各种合适的摆放方式的集合,Г=[(i,j)|(i,j)∈(1,…,n)×(1,…,k),di,j≤d*],即可以利用d*从空间{1,…,n}×{1,…,k}中选取Г恰当的子集,后续计算中只需计算集合Г内各情况的相交面积,这样只需计算少量情况下的相交面积就可以找出所要识别的目标,大大减少了计算复杂度,提高了处理的实时性。 链表是一种物理存储单元上非连续、非顺序的存储结构,而双向链表主要特点是它的每个数据节点都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表任意一个节点开始,都可以很方便地访问它的前驱和后继节点。利用此结构可以确定每一点和相邻两点间的关系,便于实现交点的快速插入。本节对文献[7]中的算法进行改进,使算法适用于所有相交多边形。 算法基本思想是将两多边形顶点按逆时针方向分别依次放入双向链表中,从一个是入点[8]的交点处逆向行进,当碰到交点时,对交点类型进行判断以确定是沿原链表继续向前还是转至另一多边形链表,如此依次判断直至回到初始入点,即得到多边形的一个交。再从剩余未遍历交点选取一个入点重复上述操作,直至所有交点都被遍历。对于多边形边重合的情况,只考虑相交部分两端点为相交点。以图3图形为例说明该算法,具体步骤如下: 输入:两多边形A、B逆时针顶点序列{A1,A2,A3,A1},{B1,B2,…,B8,B1}。 输出:两多边形的相交部分逆时针方向坐标。 步骤 1:A1,A2,A3,A1→A链表; B1,B2,B3,B4B5,B6,B7,B8,B1→B链表。 步骤 2:交点插入链表具体步骤如下: 定义交点个数CountI,并赋值为0; for(i=1;i<4;i++) for(j=1;j<9;j++) {If(多边形A的第i条边与B的第j条边相交) 判断交点个数赋值给CountI; If(CountI==1) {求出交点I坐标; 将I插入到A链表第i个点与第i+1个点之间; 将I插入到B链表第j个点与第j+1个点之间;} Else if(CountI>1) {求出交线的两端点I1、I2,其中I1靠近第i个顶点; 将I1、I2插入到A链表第i个点与第i+1个点之间; 将I1、I2插入到B链表第j个点与第j+1个点之间;} } 最后得到A链表:A1,I10,I6,I5,I1,A2,I2(B2),I3(B3),I4,I7(B6),A3(I8)(B7),I9,A1;B链表:B1,I1,I2(B2),I3(B3),B4,I4,I5,B5,I6,B6(I7),B7(I8),B8,I9,I10,B1 步骤 3:选取由A逆时针进入B的入点(如选择I1)对两链表进行遍寻求两多边形交集过程如下: 从I1开始,沿A链表行进; 执行如下判断: If(遍历到入点交点) {If(交点是原多边形顶点) {If(交点也是另一多边形顶点) {沿原多边形链表继续行进至下一交点即重叠线段末端; If(逆时针走向时交点相对于另一多边形为入点) 沿原多边形链表继续遍历; Else 转至沿另一多边形链表遍历;} Else 转至沿另一多边形链表遍历;} Else沿原多边形链表继续行进;} Else 继续遍历寻找入点交点; 步骤 4:检测是否所有交点均已被遍历,若否,则从未遍历的交点中选取一入点,按以上步骤继续遍历,直至所有交点均被遍历,输出相交多边形,算法结束。如图3,I6是由多边形B进入多边形A的入点,故从I6开始先沿B链表遍历,到达I7,I7、B6、A3三点合一,判断知两多边形存在边部分重合,沿链表B继续行进,至I8,I8是由多边形B到A的出点,故转入A链表,沿A遍历,按上述步骤直至起始入点I6,得到点I6,B6(I7),A3(I8)(B7),I9,I10,I6,依次连接得到另一相交多边形,输出相交多边形,算法结束。 图3 改进型双向链表求交集 为了验证上文所提算法的可行性,在VC++6.0平台上对不同目标进行了大量识别仿真实验。图4为其中部分仿真轮廓匹配图,表列出了图目标轮廓匹配时的相交边、重心距离以及相交面积。其中项目1重合边、2重合边表示多边形1与多边形2相重合的边在各多边形中所处的位置。从图表中可以看到,重心距离与相交面积的关系基本符合重心距离越小相交面积越大,从而证明了摆放算法的可行性;对于真正匹配的图像在摆放方式正确情况下其相交面积远远大于其他匹配图形相交面积,如图表中(b4)面积远大于其他匹配图形面积,则(b4)对应模板库中的目标就是所要寻找的目标。从仿真可以看出,此算法能够正确识别目标。 本文所提算法对飞机、舰船甚至手势等目标都可以进行识别,在识别过程中利用双向链表每一节点处都可方便访问前驱节点和后继节点的结构特点存储目标轮廓多边形与模板库目标多边形交集顶点,从而得到交集多边形,最终通过交集面积的比较来确定所要识别的目标。整个过程简便易操作,并且克服了统计特征识别的不利影响。 图4 目标轮廓匹配图 [1] Elghazal A, Basir O, Belkasim S. A novel curvature-based shape Fourier descriptor[A].15thIEEE international Conference on Image Processing[C].2008:953-956. [2] 周秀芝,刘 方,王润生. 利用局部不变特征识别复杂平面多边形[J].计算机辅助设计与图形学学报,2003,15(7):858-862. [3] 国新毅. 高速自动化灌装线上视觉检验系统研究[D].济南:山东大学,2009. [4] 滕召荣,蒋天发. 邻域平均法对矢量图平滑处理[J].现代电子技术,2009(14):75-77. [5] 何东健.数字图像处理[M].西安:西安电子科技大学出版社,2003. [6] Kashyap R L,Oommen B J.A Geometrical Approach to Polygonal Dissimilarity and Shape Matching [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1982, 4 (6):649-654. [7] 宋立明,闫浩文,王邦松,等.两个简单多边形求交的算法[J]. 测绘与空间地理信息,2011,34(6):258-260. [8] 何 研.2-D不规则多边形演化布局求解的干涉量计算研究[D].湘潭:湘潭大学,2011. A New Target Recognition Algorithm Based on Geometric Difference Wang Yanfang1, Feng Qi1, Deng Xiujian2 (1.School of Electronic Information,Northwestern Polytechnic University,Xi’an 710072,China;2.Science and Technology on Avionics Integration Laboratory,Shanghai 200233,China) In order to reduce the complexity of the target recognition and improve their noise immunity, a geometric-difference based recognition method is presented. First, exact contour of target picture after image processing, and construct approximate polygon outline of target image using a minimum perimeter polygon method. Then zoom in the two polygons according to standard targets in template library to get the same area. And make target contour parts overlap with standard contour using the placement algorithm. After that, we introduced a new algorithm called modified two-way chain table algorithm to get intersection area, and recognized the target according to intersecting area. The simulation experiments show that this method is simple and can quickly identify the target. target recognition; polygon fitting; polygon intersecting area; doubly linked list 2015-08-18; 2015-10-26。 航空科学基金资助项目(20145553028);西北工业大学研究生创意创新种子基金(22016126)。 王彦芳(1991-),女,山东济宁人,硕士研究生,主要从事航空火力控制及目标识别方向的研究。 1671-4598(2016)07-0156-03 10.16526/j.cnki.11-4762/tp.2016.07.041 TP301 文献标识码:A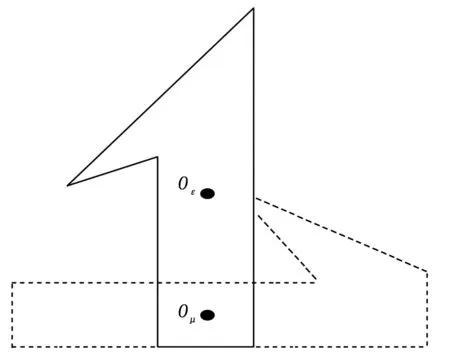
3 多边形交集求取
4 实例仿真
5 结束语