基于邻域粗糙集和并行神经网络的故障诊断

明 阳，周 俊

(1.中航商用航空发动机有限责任公司，上海 200241；2.华中科技大学 能源与动力工程学院，武汉 430074)

基于邻域粗糙集和并行神经网络的故障诊断

明 阳1，周 俊2

(1.中航商用航空发动机有限责任公司，上海 200241；2.华中科技大学 能源与动力工程学院，武汉 430074)

针对目前使用神经网络诊断故障时出现的输入向量选择困难、网络结构复杂、对并发故障诊断效果不好等问题，提出了基于邻域粗糙集和并行神经网络的故障诊断方法；先利用邻域粗糙集对初始征兆进行约简，留下有价值的征兆作为神经网络的输入向量，然后针对每种故障类型设计一个神经网络；用多个训练好的神经网络来并行诊断故障，综合每个神经网络的结果给出最终的诊断结论；用转子实验台的实验数据对这种故障诊断方法进行验证，结果显示该方法能优化神经网络结构，且神经网络具有训练速度快、诊断正确率高的特点。

故障诊断；邻域粗糙集；神经网络；并行网络结构

0 引言

随着现代科学技术水平的日益提高，旋转机械的规模和复杂程度也在迅速增加，其安全性和可靠性问题越来越突出，安全保障已经逐渐成为系统运行的一个重要组成部分。同时，故障诊断技术也呈现出更宽泛、更深入和更有效的发展态势。

目前，神经网络技术已经广泛应用在故障诊断领域，并取得了很好的效果，但同时也存在着不少问题。大型复杂旋转机械有着故障类型多、信号来源多、信号特征多等特点，由于诊断每种故障所需要的征兆通常不一样，造成神经网络的输入特征向量选取困难，同时为了有效诊断故障一般需要提取大量的故障征兆，但其中有些征兆可能是冗余的，直接作为神经网络的输入向量会造成网络结构复杂、网络收敛速度慢等问题。另外单个神经网络对并发故障的诊断效果也不好。

邻域粗糙集是一种属性约简方法，是针对经典粗糙集的改进，可以直接对连续型数值属性进行约简。针对神经网络在故障诊断中出现的以上问题，本文提出了基于邻域粗糙集和并行神经网络的旋转机械故障诊断方法。首先利用邻域粗糙集对提取的征兆进行约简得到有价值的征兆作为神经网络的输入向量，解决神经网络输入向量选取困难的问题。然后针对每种故障类型设计一个诊断神经网络，用训练好的多个神经网络来并行诊断故障。最后综合每个神经网络的结果给出最终的诊断结论。本文用转子实验台模拟几种常见的故障用于验证该方法的诊断效果。

1 神经网络及其在故障诊断中的弊端

神经网络依靠系统的复杂构造，通过调整内部大量节点(神经元)之间相互连接的关系，得到输入和输出之间的映射关系，从而达到信息处理的目的[1]。BP神经网络是一种单向传播的多层前馈神经网络，是目前使用最广泛的神经网络之一，本文以BP神经网络为例进行方法论述。

BP神经网络有一个很重要的定理：对于任何闭区间内的一个连续函数都可以用单隐含层的BP网络逼近，一个三层BP网络就可以完成任意n维到m维的映射。典型3层BP神经网络的拓扑结构如图1所示。

图1 典型3层BP神经网络拓扑结构图

在上图中，X1，X2，…，Xn是BP神经网络输入向量的值，Y1，…，Ym是BP神经网络输出向量的值，ωij和ωjk为BP网络的权值。BP神经网络可以看作一个非线性函数，完成n维输入到m维输出的非线性映射。

旋转机械发生不同故障时，相应的故障征兆也将发生变化。故障类型与故障征兆之间存在着某种函数关系，一般来说，这种关系是非线性的。故障诊断是典型的模式识别问题，神经网络是一种很好的模式识别方法，通过训练可以得到故障征兆与故障类型之间的映射关系，然后用训练好的网络来进行故障诊断。

目前使用神经网络进行故障诊断时会出现以下几个弊端。

1)输入向量选择困难：为了监测设备的运行状态，通常会在设备上布置很多传感器获取设备的信号数据，分析后得到设备运行状态征兆。对于故障模式多的大型复杂旋转机械，由于诊断每种故障所需要的征兆通常不一样，造成输入向量选择困难。目前神经网络的输入向量基本是依照经验人为选定的，输入向量选择的好坏对故障诊断效果的影响很大。

2)选择的征兆有冗余：神经网络输入向量的维数是固定的，为了有效诊断故障一般需要提取大量的故障征兆，但其中有些征兆可能是冗余的，直接作为神经网络的输入向量会造成网络结构复杂、网络收敛速度慢等问题。

3)对并发故障诊断效果差：设备运行时经常会出现并发故障，由于我们基本上不会用并发故障的样本来训练网络，在出现并发故障的情况下很容易误诊。

2 基于邻域粗糙集的属性约简

Pawlak教授于1982年提出了粗糙集(Rough sets)理论[2]，这是继概率论、模糊集、证据理论之后的又一个处理不确定性的数学工具，可以对数据进行分析和推理，从中发现隐含的知识，揭示潜在的规律。但是粗糙集定义在经典的等价关系和等价类基础上，只适合处理离散型属性，对于现实应用中广泛存在的连续型数值属性却不能直接处理。研究人员在利用粗糙集来处理该类数据时，往往要先采用离散化算法把连续型数值属性离散化，但这一转换不可避免地带来了信息损失，会改变数据原始的属性性质，而且计算处理的结果在很大程度上取决于离散化的效果。

为了解决经典粗糙集不便于处理连续型数值属性的问题，胡清华在2008年提出了邻域粗糙集的数值约简方法，这种方法不需要对连续的数值变量进行离散即可对属性进行约简[3]。此后邻域粗糙集被用于特征选择[4-5]、数据分类[6-7]、故障诊断[8-9]等领域。

邻域粗糙集的邻域概念是根据在某一度量上中心点到边界的最大距离进行定义的，给定实数空间上的非空有限集合U={x1，x2，…，xn}，对于U上的任意对象xi，定义其δ-邻域为:

(1)

其中:Δ(x,xi)为x到xi的距离，δ(xi)称为由xi生成的δ邻域信息粒子。

故障诊断问题是具有条件属性和决策属性的信息系统，也称为决策表，用T=(U,C∪D)表示，其中U是对象的非空有限集合，称为论域，即所有的样本；条件属性集C和决策属性集D组成属性的非空有限集合。一般来说决策表中的所有条件属性对于决策而言并非同等重要，甚至有的属性是冗余的，去除冗余属性并不会影响决策结论的推导。

决策属性D将U划分为N个等价类：X1，X2，…，XN，∀B⊆C，定义决策属性D关于B的下近似为:

(2)

其中:B_Xi={Xi}δB(xi)⊆X,xi∈U},δB(xi)是由属性B和距离Δ生成的邻域信息粒子。

决策属性D的下近似也称为决策正域，记为POSB(D)。定义决策属性D对条件属性B的依赖性为:

(3)

0≤γB(D)≤1，显然，正域越大，决策属性D对条件属性B的依赖性越强。γB(D)是单调的，如果B1⊆B2⊆…⊆CB1⊆…⊆CB1⊆B1⊆…⊆C，则γB1(D)≤γB2(D)≤γC(D)。

对于B⊆C，如果B满足以下条件(1)∀α∈B，γB-α(D)<γB(D)；(2)γB(D)=γC(D)。则称B为C的一个约简。与经典粗糙集一样，约简并不是唯一的。为了快速找到合适的约简，胡清华提出了前向贪心约简算法[10]，该算法以条件属性在决策系统中的重要程度为提取标准。依赖性定义了条件属性对分类的贡献，可以作为属性重要度的评价指标。该算法以空集为起点，每次计算全部剩余属性的属性重要度，从中选择属性重要度值最大的属性加入约简集合中，直到所有剩余属性的重要度为0，即加入任何新的属性，系统的依赖性函数值不再发生变化为止。这种算法能够确保重要的属性首先被加入到约简中，从而不损失重要的特征。

3 邻域粗糙集与并行神经网络结合

在设计神经网络时，我们希望尽量减少输入向量维数的同时能够达到较好的故障诊断效果。邻域粗糙集通过挖掘数据间的关系，可以去掉冗余的信息。将邻域粗糙集与神经网络结合，可以简化神经网络的输入向量。另外为了解决单个神经网络对旋转机械并发故障诊断效果不好的问题，分为多个小型神经网络来并行诊断故障，一个神经网络诊断一种故障。

基于邻域粗糙集和并行神经网络的故障诊断方法的步骤如下：

(1)确定所需要诊断的故障类型，通过大量实验得到各故障状态下的原始样本数据，利用各类信号特征提取方法提取原始样本信号的特征。可以将故障类型差别大的分开处理，例如将转子系统故障、轴承故障和齿轮故障分开，分别提取对故障敏感的特征量，形成多个初始决策表，然后分别进行下面的步骤。

(2)用邻域粗糙集对初始决策表进行属性约简，得到约简后的决策表。

(3)按照下面的方法设计并行神经网络

输入层：根据约简后剩余的属性确定输入向量，输入维数为N。设第i个神经网络的输入向量有n个特征参数，则这个神经网络的输入节点个数为n。

输出层：输出层只有一个节点(L=1)，对应这个神经网络诊断的故障模式。

(4)用约简后的决策表训练神经网络，每个神经网络单独训练。为了消除各个属性之间的数量级和量纲的差异，输入神经网络之前要进行归一化处理。将该故障模式的典型样本和非该故障模式的典型样本输入神经网络中训练，用当前故障模式的样本训练对应的神经网络时输出为1，其他的样本训练时输出为0。

(5)故障诊断时，可以根据需求将诊断样本同时输入到所有或者个别神经网络中得到输出，然后根据各个神经网络的结果得出最终的诊断结论。若某个神经网络的输出结果大于设定的阈值时(比如可以设定阈值为0.7)，判断设备出现了这个故障。如果某几个神经网络的输出结果都大于设定的阈值，则设备可能同时出现了这几种故障。在某些情况下，如果所有的神经网络的输出结果都小于某个阈值，则可以认定设备没有发生故障。

图2 基于邻域粗糙集的属性约简与神经网络训练步骤图

传感器安装在旋转机械设备上，通过采集器采集传感器的数据，然后利用信号特征提取方法提取所需要的信号特征。并行神经网络故障诊断的原理示意图如图3所示。

图3 并行神经网络故障诊断原理示意图

4 诊断效果验证

用转子实验台模拟不平衡、支座松动和不对中3种不同的转子系统故障。在实验台上布置5个电涡流传感器测转子轴的径向振动，传感器的布置如图4所示。

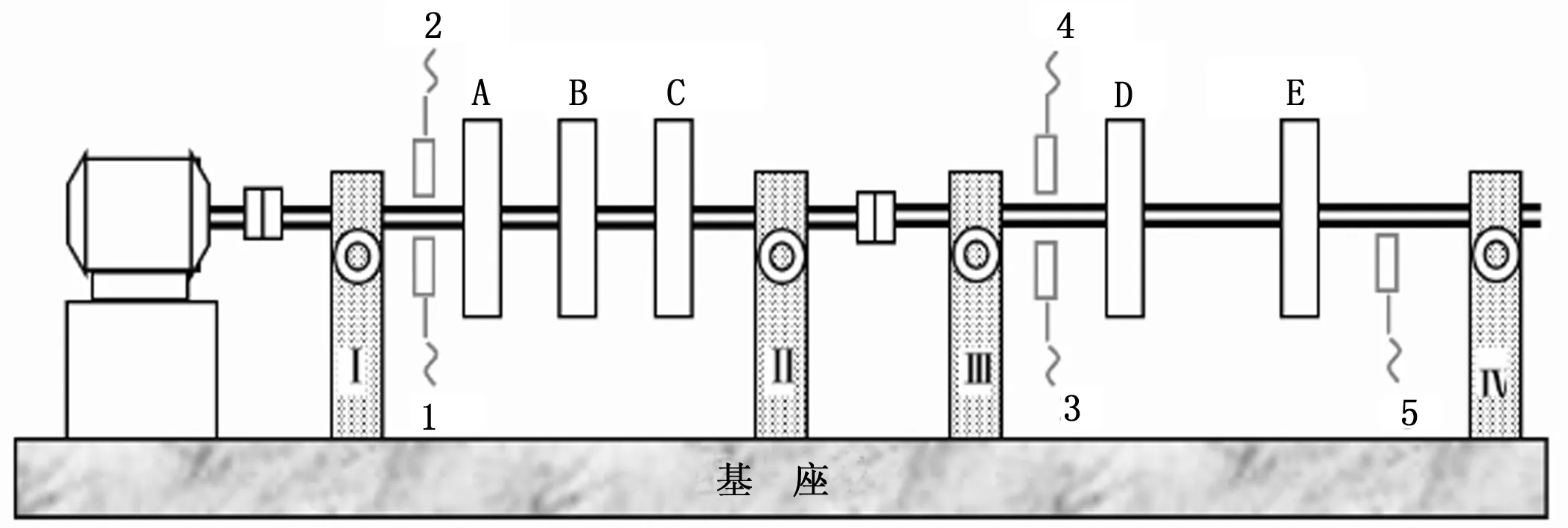
图4 转子实验台布置示意图

实验台模拟实际工作中的升降速过程，并且在转速为3000 RPM左右时稳定工作一段时间，每种故障状态下做4次实验，每次实验采集50组振动波形与转速数据，总共得到600组振动波形与转速数据。

选取一些对转子系统故障敏感的特征量进行分析。有效值可以表征振动波形的能量，并随着转速的增加而增大，为了体现故障的内在特征，取有效值与转频的比值。波形指标表示实际波形与标准正弦波的差异和畸变，可以用于低频领域的不平衡和不对中的区分。与转子系统故障相关的频率特征点一般在3倍频以下，可以取1倍频到3倍频的幅值，同时为了更好地体现这3个频率点幅值之间的大小关系，取这3个频率点幅值与这三个幅值中的最大值的比值。小波分析是一种新型的时频分析方法，对信号进行连续小波变换后得到的小波系数可以作出小波灰度图，小波一阶灰度矩[11]是小波灰度图的矩特征，由于不同类别故障的小波灰度图表现出一定的差异，所以可以用小波一阶灰度矩进行故障识别。这样每个传感器的数据提取6个特征量再加上实验台的转频(单位为Hz)作为最初的条件属性，故障类型作为决策属性，得到拥有600个样本的初始决策表。

用邻域粗糙集对初始决策表进行属性约简，将冗余的属性约简掉，剩余的属性为实验台的转频和其他15个属性，被约简的属性用“——”标识出来，如表1所示。将初始决策表中的冗余属性去除，得到约简后的决策表。

表1 被约简的属性

利用Matlab设计3个BP神经网络分别诊断不平衡故障、支座松动故障和不对中故障。选择三层网络结构，对每个BP神经网络的参数做统一设定[12]，隐含层神经元的传递函数采用正切函数tansig，输出层神经元传递函数采用S型对数函数logsig，满足输出模式为0-1的要求。输入层神经元个数为16个，隐含层节点数的选择参考公式(1)选为14个。网络的结构如图5所示。

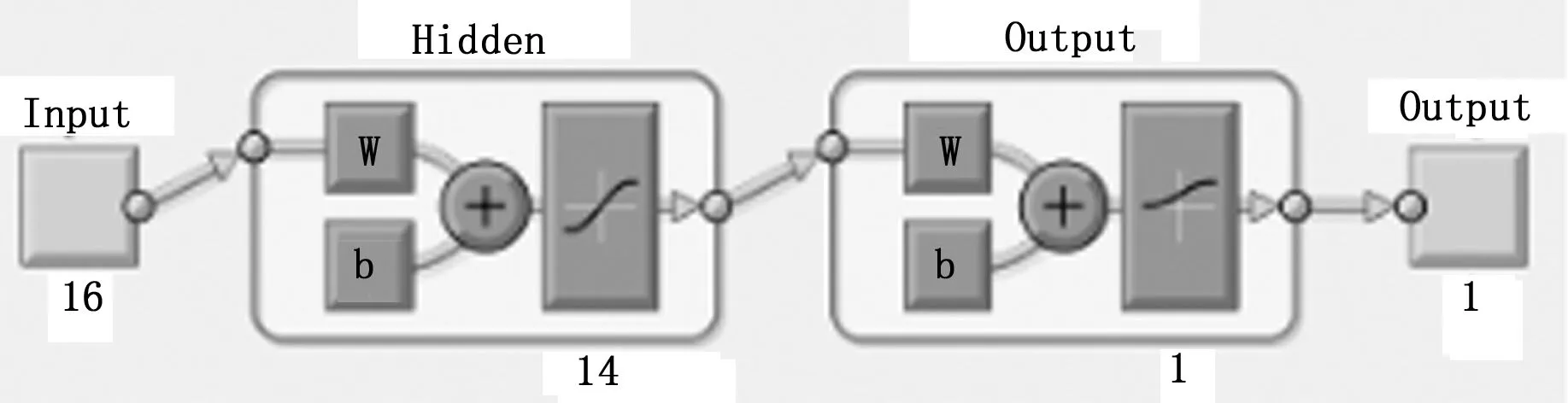
图5 并行BP神经网络结构

从约简后的决策表中选取每种故障的150组样本作为网络的训练样本，另外每种故障的50组样本作为网络的测试样本。首先用训练样本训练神经网络，然后对训练好的网络用测试样本进行测试。

输入神经网络之前对数据进行了归一化处理使输入向量的范围在-1～1之间。用相应的故障样本训练相应的网络时输出为1，其他故障样本训练时输出为0。神经网络训练达到要求后，用测试数据分别输入到这3个BP神经网络中得到的测试结果如表2所示。

表2 分3个BP神经网络并行处理结果

可以看到每个网络诊断对应的故障时平均输出结果都接近于1。同样设置某个诊断网络的输出结果大于0.7时判断发生了这个故障，结果显示故障诊断正确率为100%。

从以上的结果可以至少得出以下三个结论：(1)根据经过邻域粗糙集约简后得到的属性设计并行神经网络可以优化神经网络的结构；(2)由于神经网络的输入节点和输出节点数变少，网络的训练速度会变快；(3)同时还能保障故障诊断的正确率。

5 结语

大型复杂旋转机械有着故障类型多、信号来源多、信号特征多等特点，使用神经网络诊断故障时，会出现神经网络输入向量确定困难、网络结果复杂、对设备并发故障容易出现误诊等问题，使用本文提出的基于邻域粗糙集和并行神经网络的故障诊断方法能很好地解决这些问题。在Matlab中以BP神经网络为例设计多个并行神经网络对转子实验台模拟的故障进行诊断，结果显示根据经过邻域粗糙集约简后得到的属性设计并行神经网络可以优化神经网络的结构，神经网络训练速度快且能保障故障诊断的正确率。在实际大型复杂旋转机械的故障诊断中，此方法将会有极大的应用价值。

[1] 史忠植. 神经网络[M]. 北京：高等教育出版社，2009.

[2] Pawlak Z. Rough Sets—Theoretical Aspects of Reasoning about Data[Z]. Dordrecht: Kluwer Academic, 1991.

[3] 胡清华, 于达仁, 谢宗霞. 基于邻域粒化和粗糙逼近的数值属性约简[J]. 软件学报. 2008, 19:640-649.

[4] 谢娟英,李 楠,乔子芮. 基于邻域粗糙集的不完整决策系统特征选择算法[J]. 南京大学学报(自然科学版),2011(4):383-390.

[5] 段 洁,胡清华,张灵均,等. 基于邻域粗糙集的多标记分类特征选择算法[J]. 计算机研究与发展,2015(1):56-65.

[6] 韩 虎,党建武,任恩恩. 基于邻域粗糙集的支持向量机分类方法研究[J]. 计算机科学,2010(2):229-231+285.

[7] 刘 潇. 基于邻域粗糙集和超网络的不平衡数据分类方法研究[D].重庆:重庆邮电大学,2015.

[8] 崔建国,宋博翰,董世良,等. 基于邻域粗糙集的航空发电机健康诊断方法[J]. 数据采集与处理,2012(1):80-84.

[9] 瞿金秀,张周锁,何正嘉. 基于多小波包和邻域粗糙集的故障诊断模型[J]. 振动测试与诊断,2013(S1):137-140.

[10] 胡清华, 赵 辉, 于达仁. 基于邻域粗糙集的符号与数值属性快速约简算法[J]. 模式识别与人工智能, 2008, 21(6):732-738.

[11] 张燕平. 汽轮机轴系振动故障诊断中的信息融合方法研究[D].武汉：华中科技大学,2006.

[12] 周 品. MATLAB神经网络设计与应用[M]. 北京：清华大学出版社，2013.

A Fault Diagnosis Method Based on Neighborhood Rough Sets and Parallel Neural Networks

Ming Yang1, Zhou Jun2

(1.AVIC Commercial Aircraft Engine Co.,Ltd., Shanghai 200241,China;2.School of Energy and Power Engineering, Huazhong University of Science and Technology, Wuhan 430074, China)

Using neural network to diagnose the faults may occur the problems such as difficult selection of input vector, complex structure of network and ineffective for simultaneous fault diagnosis. For that reason, this paper proposes a fault diagnosis method based on neighborhood rough sets and parallel neural networks. We first use neighborhood rough sets to reduce the initial signs. The remaining valuable signs will be used as the input vector of neural network. Then we design neural networks for each type of fault. We use the trained neural networks to diagnose the faults in parallel and give the final diagnosis conclusion according to the results of each network. We have tested the method by using the experimental data of rotor test stand and found that this method can optimize the structure of neural network and the networks need less training time and can ensure the accuracy of fault diagnosis.

fault diagnosis; neighborhood rough sets; neural network; parallel networks

2016-01-13；

2016-02-26。

明 阳(1983-)，女，博士，主要从事旋转机械振动信号采集、分析处理，与振动故障诊断方向的研究。

1671-4598(2016)07-0042-03

10.16526/j.cnki.11-4762/tp.2016.07.012

TH165.3 文献标识码：A