基于重要度的分级贝叶斯网络诊断模型研究

牛 伟，牛文生，成 娟

(1.中航工业西安航空计算技术研究所，西安 710065；2.西安应用光学研究所，西安 710065)

基于重要度的分级贝叶斯网络诊断模型研究

牛 伟1，牛文生1，成 娟2

(1.中航工业西安航空计算技术研究所，西安 710065；2.西安应用光学研究所，西安 710065)

为了提高复杂系统故障检测和诊断的准确性，从数据的不确定性、诊断的不确定性以及特征参数选择的不确定性三方面展开研究；在贝叶斯网络解决不确定性问题优势的基础上，提出了基于重要度的分级贝叶斯网络模型；以往基于贝叶斯网络的方法无法做到系统地选择参数，建立的模型都是全模型；虽然全模型没有遗漏关键的参数，但包含了很多不必要的参数，这些多余参数不仅会对诊断造成不良影响，导致拖尾效应；仿真结果表明，提出方法可以获得更佳的故障特征，有利于提高故障识别能力，验证了模型的有效性。

故障诊断；贝叶斯网络；后验分布；层次分析法

0 引言

现代航空发动机系统内部构造异常复杂，故障问题涉及的单元多以及单元之间的关系难以判断等原因，再加上人为操作原因，使得武器系统故障诊断中存在大量的不确定性等问题。通过研究发现[1-5]，故障诊断中目前存在的三类问题，以往算法并没有解决。

第一类是关于数据的有效性。武器系统中包含的传感器由很多部件组成，比如灵敏元件、变换器和通信设备等。当其中任意部件发生故障，传感器信号将会与正常信号不同，这些不同表现为浮动、偏差和精度降级。

故障诊断是通过观测系统的行为，来判断其健康状态。然而，通常情况下从传感器获得的数据必不可少的包含随机噪声，有时候甚至包含某类偏差或错误，使用这些数据将会导致故障诊断质量的降低。因此，在进行故障诊断之前，需要保证数据的有效性。

第二类是关于诊断的多重解。目前诊断算法大都是将故障诊断问题转换成一个最优化问题，即在满足一定约束条件下，通过最小化或最大化一个目标函数进行求解。求得的解只是解空间中的一个点，即多个近似解中的一个解，其余的近似解都被舍弃，解的唯一性得不到保证。因此，在故障诊断问题中可能存在多个解，但是通过最优化方法求解不能表述多个解。

第三类是关于诊断中参数的选择。如果选择了一些不必要的参数，目前算法将会过高评估不必要的参数，而低估必要的参数，这种现象被称为“拖尾效应”。如果一些必要的参数被忽略，结果将是不正确的。一个参数是否必要依赖于系统中的数据是如何产生的。当然，在现实问题中，不可能预先知道所有参数是否必要。因此，在故障诊断问题中，参数的选择存在模糊性。不正确的选择将会导致拖尾效应或者错误的结果。

这三类问题可以归结为：数据的不确定性、诊断的不确定性以及参数选择的不确定性。在此基础上，引出了本文的研究点：

(1)如何在数据包含误差的情况下进行故障诊断？

(2)如何识别故障诊断中出现的多重解？

(3)如何解决选择参数时的模糊性问题？

针对上述3个不确定性问题，通过对贝叶斯网络的深入研究[6-11]，首次提出结合重要度的分级贝叶斯网络故障诊断模型，实现将多个不同复杂度贝叶斯网络模型按照重要度排列，构建分级模型。该模型将数据误差处理成参数，和状态参数一起进行估计；将估计问题转换成基于贝叶斯网络的概率推理问题；提出的分级结构减轻由于参数增加引起的拖尾效应。实验结果表明：提出模型很大程度上提高了诊断的准确性，验证了该模型的有效性。

1 分级贝叶斯网络诊断模型

1.1 系统建模

令X=(X1,X2,...,Xn)为未知状态向量，Y=(Y1,Y2,...,Yn)为观测向量，X和Y之间的关系f表示为:

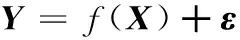
(1)

式中，ε代表传感器的随机噪声。

假定运行条件，使关系f能够线性化，即:

(2)

式中，A为系数矩阵。这里，ε不仅包含随机噪声，还包含了线性化过程中的误差。

当传感器存在故障时，式(2)变为:

(3)

不失一般性，在给定X和B的条件下，令Y的条件概率p(Y|X,B)服从多元正态分布N(μ,τ)，μ为均值向量，τ为矩阵精度。

给定X和B，均值向量μ可以表示为:

(4)

式中，bi为系数矩阵A中的元素；l为状态参数的个数。

根据不充分证据原则，没有证据去证明一个未知状态参数Xi可能的取值，即可以在取值范围内任意取值。因此，假定Xi服从均匀分布U(a,b)，其中a和b分别为U(a,b)的上边界和下边界。同理，假设偏差B也服从一个均匀分布。

1.2 结合重要度的贝叶斯网络模型

令θ为未知状态向量X和偏差向量B的集合，即:

θ称为参数集合。建立的模型可以包含θ中所有的元素，也可以包含θ的一个子集，即可建立模型的数量为2n(n=l+m)，n为θ中元素的个数。这2n个模型之间包含的参数不同，当模型中含有某个参数，就需要对这个参数进行估计；相反，当一个参数没有被包含在模型中，那么它被指定为一个已知值。

以往基于贝叶斯网络的方法建立的模型都是全模型，虽然全模型没有遗漏关键的参数，但包含了很多不必要的参数，这些参数不仅对诊断造成不良影响，导致了拖尾效应，而且增加了建模的复杂度。

为了避免错误模型带来的风险以及考虑到建模的复杂度，提出了一个分级贝叶斯网络诊断模型(Hierarchical Bayesian Network Fault Diagnosis, HBFD)。HBFD模型将全模型扩展为多个不同复杂度的子模型，其中每个子模型由θ中包含的不同参数组成。

为了有效地描述每个模型包含哪些参数和不包含哪些参数，引进了一个辅助变量γ，γ是一个二进制变量，取值为0和1。γ控制状态向量X和偏差向量B。因此，θ服从以下分布:

式中，θ0为特定值；δ为一个很小的数。当γ=0时，θ对应的先验均匀分布集中在特定值θ0附近；当γ=1时，先验均匀分布覆盖感兴趣的区域。因此，变量γ决定了如何选取集合θ中的参数，当参数对应的γ=1时，表示模型包含此参数，当γ=0时，表示不包含此参数。θ服从的分布如图1所示。

图1 θ服从的混合均匀分布

这2n个模型的一般形式化描述如图2所示。γ,X,Y和B为向量，每一个节点可以被它们包含的元素展开。图中如果模型m包含Xi，则对应的γi被指定为1。否则，γi被指定为0。

图2 分级模型的一般形式化描述

可以看出，提出的分级结构降低了建模复杂度，解决了选择参数时的模糊性问题，以及减轻了由于参数增加引起的拖尾效应，将错误风险平均化。因此，HBFD模型解决了提出的三类问题，即数据的不确定性、诊断的不确定性以及参数选择的不确定性。

由于组成HBFD模型的各子模型对故障发生的灵敏程度和诊断的准确程度各不相同，为了合理、充分地利用各子模型的信息，赋予各子模型不同的重要度，首次提出了结合重要度的分级贝叶斯网络故障诊断模型。

设HBFD模型由子模型Mi(i=1,2,...,k)构成，可表示为:

(5)

式中，ω=(ω1,ω2,...,ωk)为各子模型的重要度。

2 基于改进层次分析法的重要度求解方法

层次分析法(analytic hierarchy process, AHP)是一种定量分析与定性分析相结合的多目标决策分析方法[12-13]。AHP的处理过程和人们对复杂决策问题的思维、判断过程大体是一致的，该方法能够充分利用各种决策信息，计算简单，结果表述明确。但是，判断矩阵的一致性检验问题是限制AHP广泛应用的一个主要因素。以往在判断矩阵的计算过程中，专家主观经验对一致性检验的影响非常大，带有很强的随意性，从而影响了结果的准确性。为了解决这个问题，本文提出了一种构建判断矩阵的新方法，并满足一致性检验要求，求解过程如图3所示。

图3 基于层次分析法的重要度求解

(1)确定目标和评价参数；

(2)构造判断矩阵：

以A表示目标，δi和δj分别表示第i个和第j个评价参数，wij表示参数δi对δj的相对重要性数值，其取值如表1所示。

表1 判断矩阵标度及含义

根据上述符号的意义，得到判断矩阵W:

其中:wij为参数δi与δj比较所得的判断，n为评价参数的个数；

(3)由式(8)计算判断矩阵W的最优传递矩阵B:

(6)

(4)求拟优传递矩阵C为:

(7)

其中，cij=10bij；

(5)由于拟优传递矩阵C总是一致的，所以可由C直接求出权重集，即运用方根法求解C的最大特征值对应的特征向量ν:

(8)

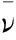
3 试验结果与分析

航空发动机是飞机的重要组成部分，航空发动机因其结构复杂及恶劣的工作环境，时刻都可能发生故障，作为飞机的心脏，它的可靠性和安全性直接影响到飞机的安全性能和飞行，其危害的严重性和维修费用的增加早已军方普遍认识。因此，以航空发动机为应用对象，对其出现的故障进行诊断，不仅可以节约维修与试验费用，而且能够提高试车效率。

在考虑传感器存在偏差的情况下，通过HBFD模型对发动机主要部件及传感器的健康状态做出评价。表2列举了发动机的状态参数与预测参数。

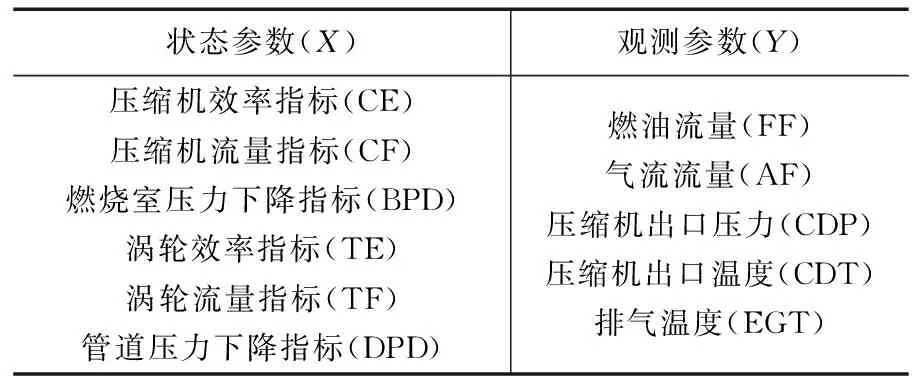
表2 某型号发动机的状态参数和观测参数

在传感器存在的故障情况下，发动机的系统模型为:

(9)

式中，状态向量X和Y同式(1)；B是偏差向量，包含5个参数。通过状态向量(X)、观测向量(Y)和偏差向量(B)建立发动机的贝叶斯网络。一般情况下，传感器之间相互独立，互不影响。本例中，由于发动机控制系统与压缩机出口压力传感器以及排气温度传感器之间关联，当压缩机出口压力传感器或排气温度传感器发生偏差，发动机控制就会发生改变，因此这两个传感器影响所有观测参数，如图4所示。

图4 状态参数、观测参数与偏差参数之间的网络结构

实验通过远程数据采集器(Remote data Collection Unit, RCU)传输的发动机数据。RCU在健康状态参数条件下工作，当一个传感器发生故障，即产生偏差，则将偏差加在相应的RCU输出中。另外，输出加入高斯随机数，用来模拟传感器随机噪声。

本例在传感器出现偏差条件下，进行某型号发动机压缩机诊断。设定压缩机效率和流量指标比正常值降低2%，记作0.98。除此之外，设定燃油流量传感器存在5%的偏差，气流流量传感器存在4%的偏差，如表3所示。

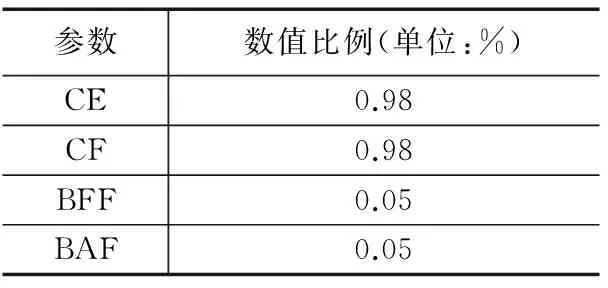
表3 参数设定

计算得到所有状态参数和传感器偏差的后验分布，如图5所示。状态参数CF、BFF和BAF的后验分布为单峰分布，每个分布的峰值与对应的实际值很接近。而状态参数CE的后验分布为多峰分布，峰值近似在实际值：0.98和基准值：1，多峰分布表明了CE的后验分布具有两种模式。在基准值：1的模式表示建立的模型不包含参数CE，即模型不包含参数CE时，CE的值被指定为1。

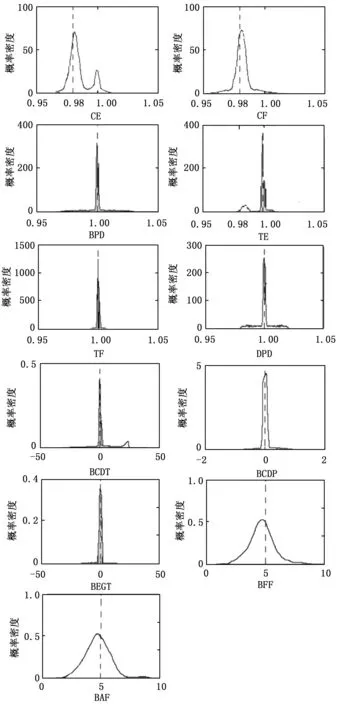
图5 状态参数的后验分布

参数CE的后验分布为多峰分布，需要进一步分析确认。通过计算辅助变量γ的后验分布，进一步确认模型。γCE和γBCDT后验分布如图6所示。γBCDT=0与γBCDT=1的概率近似相同，而γCE=1的概率近似是γCE=0概率的6倍。因此，参数CE与BCDT相比，模型更易包含参数CE。

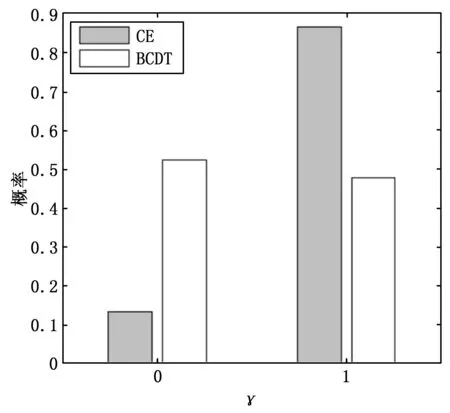
图6 γCE与γBCDT的后验分布

因此，构建的模型应该包含参数CE、CF、BFF与BAF。结果与实际情况相符合，验证了诊断的准确性。结果表明：在传感器存在故障的情况下，HBFD模型能够准确地诊断出故障，包括诊断出传感器故障，验证了HBFD模型的有效性。

4 结束语

从故障诊断中目前存在的三大问题：数据的不确定性、诊断的不确定性以及参数选择的不确定性出发，针对存在的问题，首次提出了一种分级贝叶斯网络故障诊断模型。为了充分利用各特征参数的信息，引入了层次分析法确定重要度，建立了基于改进层次分析法的模型重要度的评定方法，实现不同评定方法的有机结合。通过将多个不同复杂度贝叶斯网络模型按照重要度排列，构造了结合重要度的分级贝叶斯网络诊断模型。

以某型号航空发动机为研究对象，验证提出HBFD模型的诊断能力。仿真结果表明，该方法能够提高武器系统状态预测的自适应能力，验证了HBFD模型的有效性。

[1] Dewallef P, Leonard O, Mathioudakis K. On-line Aircraft Engine Diagnostic Using a Soft-Constrained Kalman Filter[J]. Journal of Engineering for Gas Turbines and Power, 2007, 129(4):970-976.

[2] 刘成瑞, 张庆振, 任 章. 基于分布式专家系统的运载火箭故障诊断技术[J]. 北京航空航天大学学报, 2007, 33(8):930-932.

[3] 刘成瑞, 张庆振, 任 章. 基于扩展故障树的运载火箭故障诊断专家系统[J]. 宇航学报, 2008, 29(6):1936-1941.

[4] 于德介, 陈森峰, 程军圣, 等. 基于AR模型和支持向量机的转子系统故障诊断方法[J]. 系统工程理论与实践, 2007, 27(5):152-157.

[5] 许桂梅, 黄圣国. 应用LS-SVM的飞机重着陆诊断[J]. 系统工程理论与实践, 2010, 30(4): 763-768.

[6] Ferat Sahin, M. Cetin Yavuz, Ziya Arnavut, et al. Fault diagnosis for airplane engines using Bayesian networks and distributed Particle swam optimization[J]. Parallel Computing, 2007, 33(3):124-143.

[7] Philippe W, Lionel J. Complex system reliability modelling with Dynamic object Oriented Bayesian Networks(DOOBN)[J]. Reliability Engineering and System Safety, 2006, 91:149-162.

[8] Khanafer Rana M, Solana Beatriz, Triola Jordi, et al. Automated diagnosis for UMTS networks using Bayesian network approach [J]. IEEE Transactions on Vehicular Technology, 2008, 57(4):2451-2461.

[9] Castanon Luis E Garza, Nieto González Juan Pablo, Castanon Mauricio A Garza, Morales-Menendez Rubén. Fault diagnosis of industrial systems with Bayesian networks and neural networks[A]. Lecture Notes in Computer Science, 2008, 5317 LNAI[C].998-1008.

[10] Alyson G. Wilson, Aparna V. Huzurbazar. Bayesian networks for multilevel system reliability[J]. Reliability Engineering & System Safety, 2007, 92(10):1413-1420.

[11] Sahin F, Yavuz M C, Arnavut Z, et al. Fault Diagnosis for airplane engines using Bayesian networks and distributed particle swarm optimization[J]. Parallel Computing, 2007, 33(2):124-143.

[12] 田水承, 王 曦, 王 莉, 等. 改进层次分析法的瓦斯涌出量组合预测方法研究[J]. 西安科技大学学报, 2012, 32(1):25-28.

[13] 陈 超, 张 安, 王 强. 改进层次分析法在空面多目标攻击排序中的应用[J]. 火力与指挥控制, 2012, 37(1):63-66.

Research on Hierarchical Bayesian Network Diagnosis Model Based on the Importance Degree

Niu Wei1, Niu Wensheng1, Cheng Juan2

(1.China Aeronautics Technique Research Institute, Xi’an 710065,China; 2.Xi’an Institute of Applied Optics,Xi’an 710065,China)

In order to improve complex system detect and diagnosis fault precisely, make a research from three respects: uncertainty of data, uncertainty of diagnosis and uncertainty of feature parameter selection. Based on advantages for uncertainty problem of Bayesian network, Hierarchical Bayesian for fault diagnosis is proposed. The existing algorithms are not capable of selecting variables systematically so that they generally use the full model, which may contain unnecessary variables as well as necessary variables. Ignoring this model uncertainty often gives rise to, so called, the smearing effect in solutions. Complexity and difficulty of modeling is increased. The simulation results show this method can get better fault feature, improve fault discernment, and validate the model efficiency.

fault diagnosis; Bayesian network; posterior distribution; analytic hierarchy process

2015-09-01；

2016-01-28。

中国博士后科学基金资助(2014M552504)。

牛 伟(1982-)，男，河南洛阳人，博士后，主要从事故障诊断与预测、可靠性和容错技术方向的研究。

1671-4598(2016)07-0006-04

10.16526/j.cnki.11-4762/tp.2016.07.002

TP206 文献标识码：A