分治策略下的代价敏感属性选择回溯算法*

黄伟婷，赵　红，祝　峰

1.闽南师范大学 计算机学院，福建 漳州 363000

2.闽南师范大学 粒计算及其应用重点实验室，福建 漳州 363000

分治策略下的代价敏感属性选择回溯算法*

黄伟婷1+，赵红2，祝峰2

1.闽南师范大学 计算机学院，福建 漳州 363000

2.闽南师范大学 粒计算及其应用重点实验室，福建 漳州 363000

代价敏感属性选择是数据挖掘的一个重要研究领域，其目的在于通过权衡测试代价和误分类代价，获得总代价最小的属性子集。针对经典回溯算法运行时间较长的缺点，结合分治思想，提出了一种改进的回溯算法。改进算法引入了两个相关参数，根据数据集规模自适应调整参数，并按参数大小拆分数据集，降低问题规模，以提高经典回溯算法的执行效率。针对较大规模数据集的实验结果表明，与经典的回溯算法相比，改进算法在保证效果的同时至少提高20%的运算效率；与启发式算法相比，改进算法在保证效率的同时取得了具有更小总代价的属性集合，可应用于实际问题。

粗糙集；粒计算；代价敏感；属性选择；自适应分治

1　引言

代价敏感学习是机器学习和数据挖掘领域的十大最具挑战性问题之一[1]。近十年来，代价敏感学习的研究工作受到越来越多学者的关注。贾修一等人[2]基于决策成本的最小化问题，提出了决策粗糙集模型的一种优化表示。闵帆等人[3]基于公共测试代价和属性测试顺序问题，构建了测试代价敏感决策系统的层次模型。周志华等人[4]将代价敏感学习和人工神经网络相结合，给出了决策类不平衡问题的解决方案。文献[5]将代价敏感学习引入到人脸识别领域，提出了基于代价敏感学习的人脸识别方法。

属性选择是数据挖掘的重要问题。代价敏感属性选择问题是经典属性选择问题的自然扩展。代价敏感属性选择的目的是通过测试代价[6]和误分类代价[7]之间的权衡，得到总代价最小的最优属性子集。在现实应用中，测试代价和误分类代价是普遍存在的两类重要代价。测试代价是指为获取数据而付出的代价，可以是金钱和时间等。误分类代价则是指把一个类的数据误分为另一个类而受到的惩罚，也可以用金钱等来表示。

代价敏感属性选择问题经过多年的研究发展，已经建立了一系列的理论与方法，流行的方法包括粗糙集[8]、决策树[9]、人工神经网络[4]和贝叶斯网络[10]等。Yael等人[11]基于直方图比较方法，设计了一个代价敏感适应度函数，很好地解决了代价敏感属性选择问题。杨习贝等人[12]在多粒度粗糙集基础上，建立了测试代价敏感多粒度粗糙集模型，并基于该模型提出了一个新的最小代价选择算法。文献[13]构建了一个基于置信水平的覆盖粗糙集模型，针对不同粒度的数据，动态生成测试代价和误分类代价，并给出了一种最优代价敏感粒计算方法。

目前，代价敏感属性选择问题的研究方法主要有穷举算法和启发式算法[14]。通常，启发式算法的效率高于穷举算法，而穷举算法的效果优于启发式算法。回溯法[15]是典型的穷举算法，它一般能求得最优解，但是其运行时间较长，特别是当数据集规模较大时，其效率并不理想，不能满足实际需求。本文在回溯法基础上，结合分治思想，将较大规模的数据集拆分成多个独立的、规模较小的子数据集，然后逐一求解子数据集。这样，将一个大问题分为小问题，在不影响执行效果的前提下，缩小问题规模，从而减少运行时间，提高算法效率。因此，与经典回溯法相比，本文算法能在短时间内获得理想的结果。本文采用6个UCI数据集进行实验，验证了所提算法对提高经典回溯法运行速度的有效性。

2　代价敏感属性选择问题

代价敏感属性选择问题是基于代价敏感决策系统，在权衡测试代价和误分类代价的同时，求解最小总代价属性子集。下面主要介绍代价敏感属性选择问题的相关定义。

定义1代价敏感决策系统是一个七元组[15]S=。其中U是对象的集合；C是条件属性集合；D是决策属性集合；Va是属性a的值集合；Ia:U→Va是一个信息函数；tc:C→R+∪{0}是一个测试代价函数，可以用一个代价向量tc=[tc(a1),tc(a2),…,tc(a|c|)]来表示。对任意属性子集B⊆C，属性子集B的测试代价为。mc:k×k→R+∪{0}是一个误分类代价函数，其中，可以用一个k×k矩阵来表示。mc(i,j)表示将类别i误分为类别j所导致的代价，一般情况下，mc(i,i)=$0。

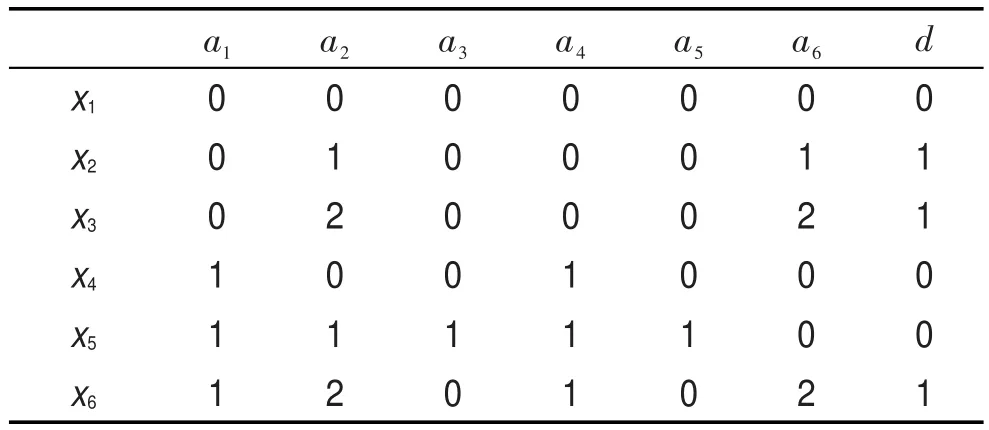
Table 1　An example of decision system表1　一个决策系统

Table 2　An example of test cost vector表2　测试代价向量

为了评价所选的属性子集是否最优，引入平均总代价的概念。设B为一个属性子集，IND(B)为U的一个划分，对象集合U′∈IND(B)，U′的误分类代价记为mc(U′,B)。对于任意的x,y∈U′，当且仅当D(x)= D(y)时，mc(U′,B)=0。而当x,y∈U′且D(x)≠D(y)时，可以将U′中的所有对象归为某一类。而在选择所属类别时，人们总是遵循最小化总误分类代价的原则，即所选的类别应使得总误分类代价最小。这里，平均误分类代价（average misclassification cost，AMC）表示为：

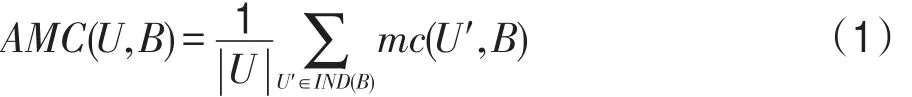
平均总代价（average total cost，ATC）表示为：

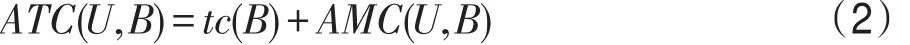
定义2设S是一个代价敏感决策系统，对于任意B⊆C，当且仅当满足，则称B为最小平均总代价属性子集。

3　分治策略下的代价敏感属性选择回溯算法

经典回溯算法通常能获得代价敏感属性选择问题的最优解，但算法效率低，特别是当处理较大规模数据集时。为此，本文引入分治策略，设计两个相关参数，提出了分治策略下的代价敏感属性选择回溯算法。本文算法的主要思想是：根据数据集规模，按条件属性拆分数据集，然后调用回溯法处理各子数据集。这样，减少了回溯算法处理的数据集规模，在保证获得最优解的同时，缩短处理时间，有效地提高了算法的效率。分治策略下的代价敏感属性选择回溯算法的主要步骤如下：

步骤1拆分数据集，每个子数据集的条件属性个数为size，子数据集总个数为Blocks=|C|/size。

步骤2调用回溯法对各子数据集求最小约简。

步骤3每次合并相邻的每k个子数据集的最小约简。

步骤4Blocks=Blocks/k。若Blocks>1，返回步骤2；否则继续执行。

步骤5对最后得到的子数据集中的每一个属性逐一进行判断：由式（2）计算每一属性删除前后的ATC，若属性去掉后ATC减小，则删除；否则保留。

下面给出分治策略下的代价敏感属性选择回溯算法（简称分治回溯算法）的伪代码。

算法1分治策略下的代价敏感属性选择回溯算法

在分治回溯算法中，S表示代价敏感决策系统；参数k表示每次参与合并的子数据集个数，即合并的路数；参数size表示初始每个子数据集所包含的条件属性个数，为了控制每个子数据集的大小，并保证多路合并时有足够多的子数据集，其值根据各个数据集条件属性总数的不同而变化，设置为size=ceil(|C|/k)－1。若参数k=1，即参数size=|C|时，分治回溯算法退化为经典回溯算法。为了提高算法的效果，在对各子数据集求解时，采用了竞争策略。

4　实验结果与分析

为了验证分治策略下的代价敏感属性选择回溯算法的有效性，本文从UCI数据库中选取6个数据集，描述如表3所示，与文献[15]中的经典回溯算法和文献[16]中的启发式算法进行实验对比。

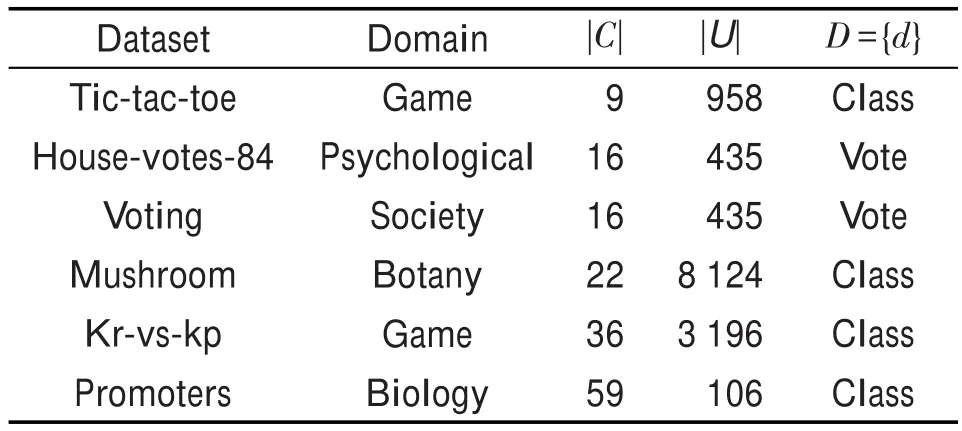
Table 3　Dataset information表3　数据集信息

4.1实验参数设置

本文采用均匀分布方式随机产生测试代价，测试代价为[1，10]区间内的整数，误分类代价设置为mc(0,1)=4mc(1,0)。另外，考虑到运行效率，根据数据集规模动态调整合并的路数k。对于前4个中小规模的数据集，设置参数k=2，参数size=ceil(|C|/k)－1；而对于最后两个较大规模的数据集，设置参数k=3，参数size=4。算法运行5次。

4.2实验结果分析

为了分析在不同误分类代价设置下，测试代价和最小平均总代价（minimal average total cost，MATC）的变化情况，设置mc(1,0)值范围为$0～$200，步长为$20。在6个数据集上，按不同参数设置执行分治回溯算法，运行结果如图1所示。

图1中，横坐标均表示mc(1,0)值，纵坐标表示代价，从图1中可以看出：

（1）MATC整体上都随着误分类代价的增长而增长。

（2）图1（b）～（d）中，当测试代价不变时，MATC随误分类代价的增加呈线性增长。

（3）图1（a）、（d）和（f）中，随着误分类代价的增大，测试代价慢慢逼近MATC。当误分类代价足够大时，测试代价等于MATC。此时，平均误分类代价为$0，表示所选的属性子集为一个约简。

（4）图1（e）中，当mc(1,0)=$20时，测试代价为$0，表示此时未进行任何测试。

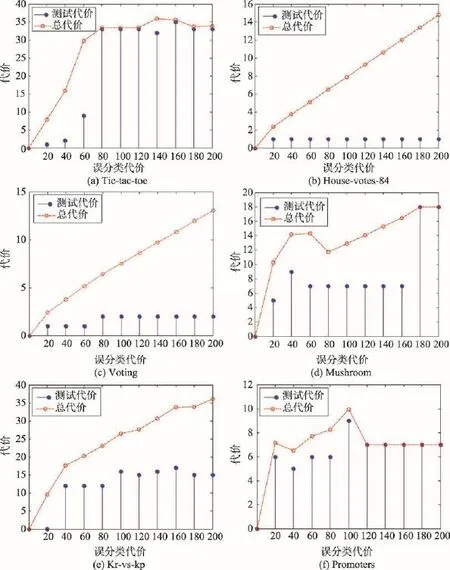
Fig.1　Test cost and minimal average total cost with different misclassification costs图1　不同误分类代价下的测试代价和最小平均总代价

为了直观地显示不同误分类代价设置下的最优属性子集及分治回溯算法的处理能力，选择较大规模数据集Promoters进行实验，设置mc(1,0)值范围为$0～$1 000，步长为$200，执行10次，运行结果如表4所示。从表4中可以看出：

（1）当mc(1,0)=$0时，平均总代价为$0，表示此时不存在惩罚代价，属性子集为空集。

（2）当mc(1,0)≠$0时，测试代价和MATC保持不变，值均为$7，属性子集的大小也不变。可见，所选最优属性子集均为约简。

为验证分治回溯算法的执行能力，选取中大规模数据集Mushroom和Kr-vs-kp进行实验。对于数据集Mushroom，分别执行分治回溯算法、文献[15]中的回溯算法和文献[16]中的启发式算法。对于数据集Kr-vs-kp，当mc(1,0)=$300时，回溯算法获得的MATC值为$48.622，略高于其他两个算法；其运行时间为1.24×107ms，而其他两个算法的运行时间仅为几百毫秒，并且误分类代价越大，必须花费更多的时间测试更多的属性，运行时间也越长。因此，为便于画图，并能更好地做对比，在数据集Kr-vs-kp中，只比较分治回溯算法和启发式算法的实验结果。实验结果对比如图2和图3所示。

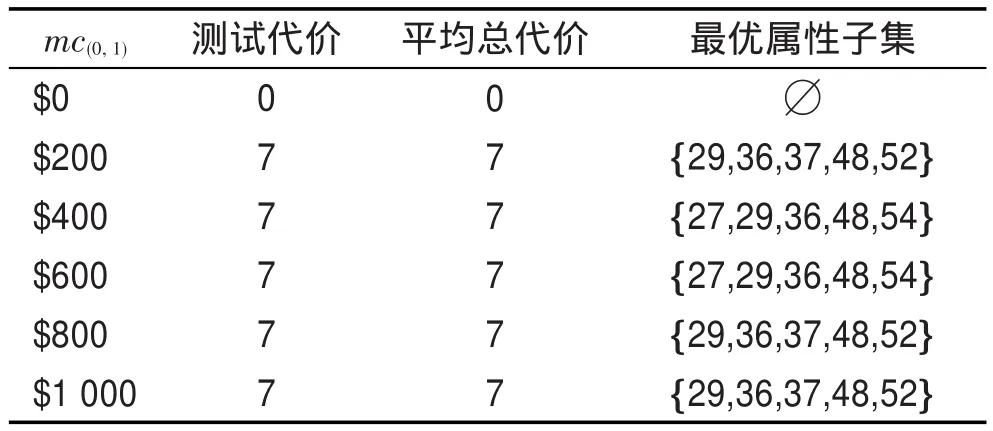
Table 4　Optimal feature subset with different misclassification costs表4　不同误分类代价下的最优属性子集

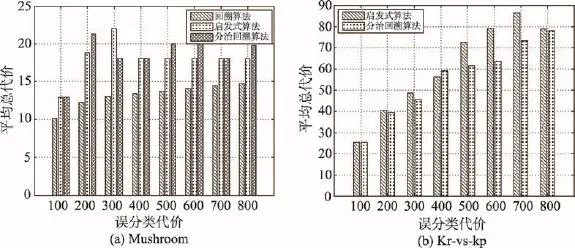
Fig.2　Comparison of minimal average total cost with different misclassification costs图2　不同误分类代价下的最小平均总代价对比

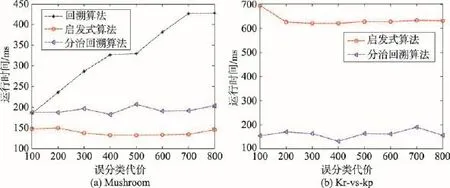
Fig.3　Comparison of runtime with different misclassification costs图3　不同误分类代价下的运行时间对比

图2和图3中，横坐标均表示mc(1,0)值，图2的纵坐标表示最小平均总代价，图3的纵坐标表示运行时间。这里，设置mc(1,0)值范围为$100～$800，步长为$100，启发式算法参数λ=－1。数据集Mushroom中，参数k=2，参数size=6；数据集Kr-vs-kp中，参数k=3，参数size=4。

从图2中可以看出：

（1）图2（a）中，回溯算法的效果最好，MATC随误分类代价的增加而缓慢增大。启发式算法和分治回溯算法的实验结果较为接近，两个算法在mc(1,0)值为$400和$700时，MATC均为$18，所求得的属性子集均为一个约简。

（2）图2（b）中，启发式算法和分治回溯算法的MATC随误分类代价的增加而增大，启发式算法的增长较快，而分治回溯算法的变化较小。从整体上看，分治回溯算法的运行效果好于启发式算法。

从图3中可以看出：

（1）图3（a）中，回溯算法的效率最差，运行时间随着误分类代价的增加基本呈线性增长。启发式算法和分治回溯算法的运行时间随误分类代价的不同并无太大变化，启发式算法结果较好。

（2）图3（b）中，启发式算法和分治回溯算法的运行时间基本保持稳定，不受误分类代价的影响。启发式算法的运行时间约为630 ms，分治回溯算法的运行时间基本为150 ms左右。可见，分治回溯算法的执行效率高于启发式算法。

5　结束语

本文提出了分治策略下的代价敏感属性选择回溯算法，根据数据集规模动态设置参数size和参数k，将问题分而治之，有效改进了经典回溯算法的效率。通过与文献[15]中的回溯算法和文献[16]中的启发式算法的实验对比，验证了本文算法的有效性。对于数据集Kr-vs-kp，设置参数k=3，参数size=4时，本文算法的效果最好。可见，将此参数设置应用到规模较大的数据集时，本文算法能获得令人满意的解。在将来的工作中，可以考虑是否有其他拆分数据集的方式，不同拆分方式下的性能是否有所区别。显然，如何快速求解多代价下的代价敏感属性选择问题是一个重点研究的课题。

[1]Yang Qiang,Wu Xindong.10 challenging problems in data mining research[J].International Journal of Information Technology&Decision Making,2006,5(4):597-604.

[2]Jia Xiuyi,Tang Zhenmin,Liao Wenhe,et al.On an optimization representation of decision-theoretic rough set models [J].International Journal of Approximate Reasoning,2014, 55(1):156-166.

[3]Min Fan,Liu Qihe.Ahierarchical model for test-cost-sensitive decision systems[J].Information Sciences,2009,179(14): 2442-2452.

[4]Zhou Zhihua,Liu Xuying.Training cost-sensitive neural networks with methods addressing the class imbalance problem[J].IEEE Transactions on Knowledge and Data Engineering,2006,18(1):63-77.

[5]Zhang Yin,Zhou Zhihua.Cost-sensitive face recognition[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2010,32(10):1758-1769.

[6]Domingos P.MetaCost:a general method for making classifiers cost-sensitive[C]//Proceedings of the 5th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining,San Diego,USA,Aug 15-18,1999.New York:ACM, 1999:155-164.

[7]Lin Ziqiong,Zhao Hong.Cost-sensitive optimal error bound selection[J].Journal of Frontiers of Computer Science and Technology,2013,7(12):1146-1152.

[8]Yao Yiyu,Zhao Yan.Attribute reduction in decision-theoretic rough set models[J].Information Sciences,2008,178(17): 3356-3373.

[9]Wang Xizhao,Dong Lingcai,Yan Jianhui.Maximum ambiguitybased sample selection in fuzzy decision tree induction[J]. IEEE Transactions on Knowledge&Data Engineering, 2012,24(8):1491-1505.

[10]Friedman N,Geiger D,Goldszmidt M.Bayesian network classifiers[J].Machine Learning,1997,29(2/3):131-163.

[11]Weiss Y,Elovici Y,Rokach L.The CASH algorithm—costsensitive attribute selection using histograms[J].Information Sciences,2013,222:247-268.

[12]Yang Xibei,Qi Yunsong,Song Xiaoning,et al.Test cost sensitive multigranulation rough set:model and minimal cost selection[J].Information Sciences,2013,250:184-199.

[13]Zhao Hong,Zhu W.Optimal cost-sensitive granularization based on rough sets for variable costs[J].Knowledge-Based Systems,2014,65:72-82.

[14]Li Huaxiong,Zhou Xianzhong,Huang Bing,et al.Decision-theoretic rough det and cost-sensitive classification[J].Journal of Frontiers of Computer Science and Technology,2013, 7(2):126-135.

[15]Min Fan,Zhu W.Minimal cost attribute reduction through backtracking[J].Communications in Computer&Information Science,2011,258:100-107.

[16]Li Xiangju,Zhao Hong,Zhu W.An exponent weighted algorithm for minimal cost feature selection[J].International Journal of Machine Learning and Cybernetics,2014:1-10. doi:10.1007/s13042-014-0279-4.

附中文参考文献：

[7]林姿琼,赵红.代价敏感最优误差边界选择[J].计算机科学与探索,2013,7(12):1146-1152.

[14]李华雄,周献中,黄兵,等.决策粗糙集与代价敏感分类[J].计算机科学与探索,2013,7(2):126-135.

HUANG Weiting was born in 1977.She received the M.S.degree in computer application from Fuzhou University in 2008.Now she is a lecturer at Minnan Normal University.Her research interests include granular computing and the study of cost-sensitive.

黄伟婷（1977—），女，福建漳州人，2008年于福州大学计算机应用专业获得硕士学位，现为闽南师范大学讲师，主要研究领域为粒计算，代价敏感学习。

ZHAO Hong was born in 1979.She received the M.S.degree in computer application from Liaoning Normal University in 2006.Now she is an associate professor at Minnan Normal University.Her research interests include granular computing and the study of cost-sensitive.

赵红（1979—），女，黑龙江哈尔滨人，2006年于辽宁师范大学计算机应用专业获得硕士学位，现为闽南师范大学副教授，主要研究领域为粒计算，代价敏感学习。

ZHU William was born in 1962.He received the Ph.D.degree in computer science from University of Auckland in 2007.Now he is a professor at Minnan Normal University.His research interests include artificial intelligence, rough sets,software watermarking and software security.

祝峰（1962—），男，江西玉山人，2007年于奥克兰大学计算机科学专业获得博士学位，现为闽南师范大学教授，主要研究领域为人工智能，粗糙集，软件水印，软件安全。

Backtracking Algorithm for Cost-Sensitive Feature Selection Based on Divide and Conquer Strategyƽ

HUANG Weiting1+,ZHAO Hong2,ZHU William2
1.School of Computer,Minnan Normal University,Zhangzhou,Fujian 363000,China
2.Lab of Granular Computer,Minnan Normal University,Zhangzhou,Fujian 363000,China

E-mail:weitinghuang92@163.com

Cost-sensitive feature selection is an important research field in the process of data mining.It aims at obtaining an attribute subset of the lowest total cost,through balancing test cost and misclassification cost.According to the shortcoming of the classical backtracking algorithm with longer running time,combining divide and conquer thought, this paper proposes an improved backtracking algorithm.Introducing two related parameters,this algorithm computes adaptively parameters according to the dataset scale,and splits the dataset with these parameters.It can enhance the efficiency of the classical backtracking algorithm by reducing the problem size.The experiments on the datasets with large scale show that this improved algorithm is effective and meets the need of practical problems.At the same time guaranteeing the effect,this improved algorithm promotes the efficiency of 20%at least than the classical backtracking algorithm.Compared with heuristic algorithm,this improved algorithm obtains an attribute set with a smaller total costand ensures the efficiency.

rough sets;granular computing;cost-sensitive;feature selection;adaptive divide and conquer

2015-09,Accepted 2015-12.

10.3778/j.issn.1673-9418.1509042

A

TP18

*The National Natural Science Foundation of China under Grant Nos.61379049,61379089,61170128(国家自然科学基金);the Key Science and Technology Project of Fujian Province under Grant No.2012H0043(福建省科技计划重点项目);the Natural Science Foundation of Zhangzhou under Grant No.ZZ2016J35(漳州市自然科学基金).

CNKI网络优先出版:2015-12-09,http://www.cnki.net/kcms/detail/11.5602.TP.20151209.1103.004.html

HUANG Weiting,ZHAO Hong,ZHU William.Backtracking algorithm for cost-sensitive feature selection based on divide and conquer strategy.Journal of Frontiers of Computer Science and Technology,2016,10(10)：1451-1458.