广义可能性计算树逻辑的两种范式*

赵　杰，李永明

陕西师范大学 计算机科学学院，西安 710019

广义可能性计算树逻辑的两种范式*

赵杰，李永明+

陕西师范大学 计算机科学学院，西安 710019

计算树逻辑（computation tree logic，CTL）的范式在模型检测方法中具有重要意义，但基于广义可能性测度的计算树逻辑的范式尚未有系统研究。为了进一步完善广义可能性计算树（generalized possibilistic computation tree logic，GPoCTL）理论，在现有的广义可能性计算树逻辑理论的基础上，参考经典计算树逻辑的范式，给出了广义可能性计算树逻辑的两种不同的范式——正态范式（positive normal form，PNF）和存在范式（existential normal form，ENF），及其对应的语构和语义解释。最后利用归纳假设法证明了任意的广义可能性计算树逻辑公式都有与之等价的PNF公式和ENF公式。

广义可能性测度；计算树逻辑；范式；模型检测

1　引言

1981年由Clarke、Emerson等人提出了模型检测方法，其作为一种形式化的自动验证技术，已被广泛应用于计算机软硬件系统、通信协议、控制系统、安全认证协议中[1-4]。它的基本思想是：通过对系统状态空间进行穷举搜索来验证系统是否满足设计规范。模型检测的一般步骤为：（1）抽象出系统的数学模型；（2）给出需要验证的性质的语言描述；（3）通过模型检测算法来计算系统是否满足该性质，如果不满足，则给出反例。

由于计算机软硬件系统复杂性的不断增加，模型中状态存在很多需要量化的信息。基于此，一些学者提出了状态迁移模型的量化扩展，如在状态中加入时间[1]，或者在模型中考虑概率[1]、可能性[5]、多值[6-7]或者统计信息[8]。1965年控制论学者Zadeh提出了模糊集理论[9-12]。进一步，为了处理含有可能性测度量化信息的模型检测，李永明等人提出了基于广义可能性测度的模型检测，形成了基于广义可能性Kripke结构的模型检测理论[13-15]。

在经典计算树逻辑（computation tree logic，CTL）模型检测中，不同的范式扮演着不同但十分重要的角色。一方面，在处理状态爆炸时，可以使用符号模型检测，其基本原理是将系统的状态转换关系用逻辑公式表示。二叉图（binary decision diagram，BDD）是用以表示逻辑公式的重要手段，有序二插图（order binary decision diagram，OBDD）作为布尔公式的一个规范的表示形式，比一般的传统公式如析取公式及合取公式能够更加紧凑地表示状态转换关系，以降低系统模型所需的内存空间[1-16]。而正态范式（positive normal form，PNF）可以有效地运用于OBDD的简化过程。另一方面，在CTL模型检测算法中，对于CTL公式的要求则为存在范式（existential normal form，ENF）公式[1]，这是由于ENF通过只处理逻辑词∃而不考虑逻辑词∀就可以计算出任意的CTL公式的结果，有效简化了模型检测算法，高效地得到结果。因此，GPoCTL（generalized possibilistic computation tree logic）范式对于GPoCTL模型检测的研究也有着极其重要的价值与意义。然而，目前对于GPoCTL范式并没有系统研究，文献[14]给出了GPoCTL公式的语构及其语义，并讨论了GPoCTL公式的一些基本性质，为GPoCTL理论奠定了基础。本文在上述工作的基础上，给出了GPoCTL公式的PNF和ENF的描述。

本文组织结构如下：第2章是预备知识；第3章引入PNF、ENF范式的语构和语义；第4章证明了任意的GPoCTL公式都有一个等价的PNF公式，以及任意的GPoCTL公式都有一个等价的ENF公式。

2　预备知识

本章给出一些基于广义可能性测度的计算树逻辑的概念，包括广义可能性Kripke结构（generalized possibilistic Kripke structure，GPKS）、广义可能性测度和GPoCTL等。详见参考文献[13-15]。

2.1广义可能性Kripke结构

定义1[14]一个GPKS是一个五元组M=(S,P,I, AP,L)，其中：

（1）S是非空可数的状态集合；

（2）P:S×S→[0,1]是可能性转移函数，并且满足对任意状态s，存在状态t，使得P(s,t)>0；

（3）I:S→[0,1]是可能性初始分布，满足存在状态s∈S，使I(s)>0；

（4）AP是一组原子命题的集合；

（5）L:S×AP→[0,1]是可能性标签函数，∀a∈AP,s∈S，有L(s,a)∈[0,1]，即为每个状态赋一个AP的模糊集合。

如果S和AP都是有穷的集合，则称M是有穷的GPKS。

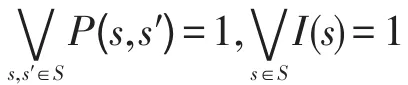
（2）可能性转移函数P:S×S→[0,1]可表示成一个模糊矩阵P=(P(s,t))s,t∈S，并称P为M的模糊转移矩阵。

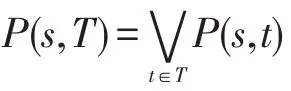
上式中的“∨”表示上确界，“∧”表示下确界[13]。特别的P*定义为：P*=P0∨P+，其中P0表示单位矩阵。

（4）令Paths(M)表示M中所有状态路径π= s0s1s2…,满足∀i≥0,P(si,si+1)>0所构成的集合，用Paths(s)表示M中所有从状态s出发的无穷路径全体构成的集合。

2.2广义可能性测度

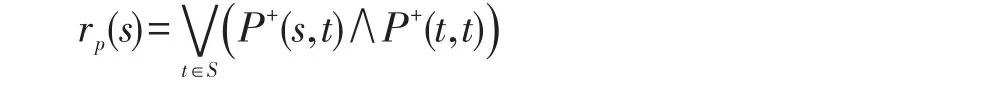
2.3GPoCTL

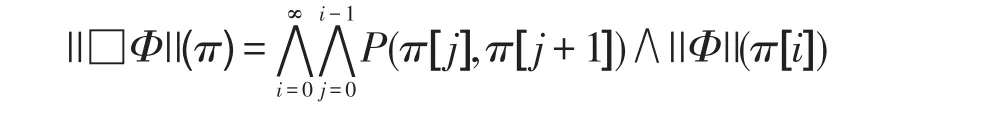
3　GPoCTL的PNF范式和ENF范式

文献[14]已对GPoCTL的语义做了详细的解释，下面给出其在PNF范式和ENF范式下的语构和语义解释。

3.1GPoCTL的PNF范式的语法

3.2GPoCTL的ENF范式的语法

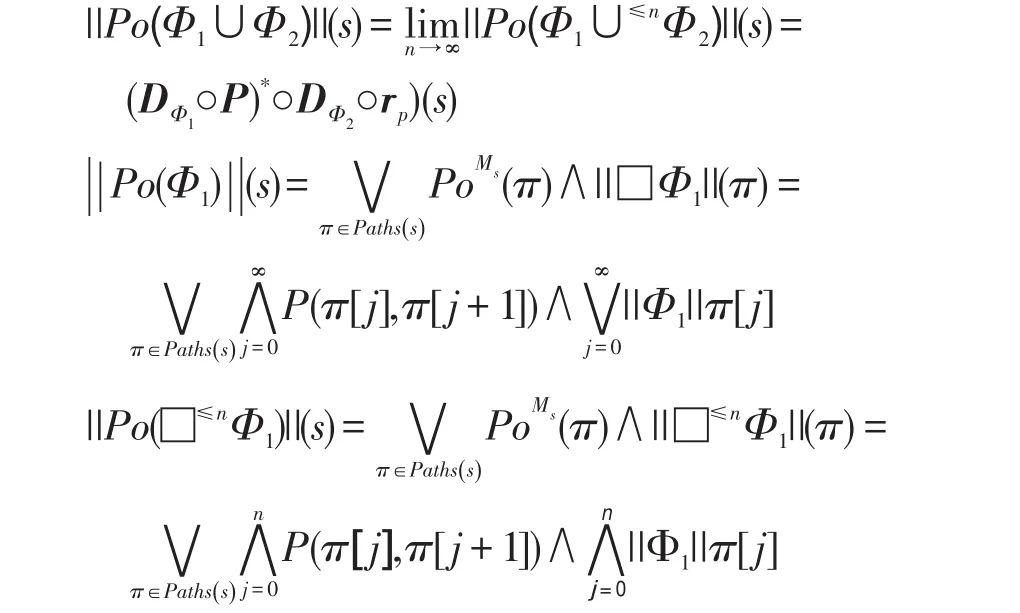
4　GPoCTL公式在PNF和ENF范式下的等价

5　结论

本文给出了广义可能性测度下计算树逻辑的两种范式及其对应的语构和语义解释，并证明了任意的GPoCTL公式都存在这两种范式下与之等价的公式，为处理GPoCTL公式的转换、GPoCTL模型检测算法的实现以及状态爆炸等问题打下了基础，同时进一步完善了现有的广义可能性模型检测理论。

[1]Baier C,Katoen J P.Principles of model checking[M].Cambridge,USA:MIT Press,2008.

[2]Clark E,Grumberg O,Peled D.Model checking[M].Cambridge,USA:MIT Press,1999.

[3]Rozier K Y.Linear temporal logic symbolic model checking[J]. Computer Science Review,2011,5(2):163-203.

[4]Lin Huimin,Zhang Wenhui.Model checking:theories,techniques and applications[J].Chinese Journal of Electronics, 2002,30(12A):1907-1912.

[5]Li Yongming,Li Lijun.Model checking of linear-time properties based on possibility measure[J].IEEE Transactions on Fuzzy Systems,2013,21(5):842-854.

[6]Lei Lihui,Duan Zhenhua.An extended deterministic finite automata based on possibility measure[J].Journal of Software,2007,18(12):2980-2990.

[7]Chechik M,Devereux B,Easterbrook S,et al.Multi-valued symbolic model-checking[J].ACM Transactions on Software Engineering and Methodology,2003,12(4):371-408.

[8]Fischer D,Gradel E,Kaiser L.Model checking games for the quantitativeμ-calculus[J].Theory of Computing Systems, 2010,47(3):696-719.

[9]Kwiatkowska M,Norman G,Parker D.Stochastic model checking[M]//Formal Methods for Performance Evaluation. Berlin,Heidelberg:Springer,2007:220-270.

[10]Zadeh L A.Fuzzy sets[J].Information and control,1965,8 (3):338-353.

[11]Li Yongming.Analysis of fuzzy systems[M].Beijing:Science Press,2005.

[12]Wang Xizhao.Fuzzy measures and fuzzy integral and its application in the classification technique[M].Beijing:Science Press,2008.

[13]Li Yongming,Li Yali,Ma Zhanyou.Computation tree logic model checking based on possibility measures[J].Fuzzy Sets and Systems,2015,262:44-59.

[14]Li Yongming,Ma Zhanyou.Quantitative computation tree logic model checking based on generalized possibility measures[J].IEEE Transactions on Fuzzy Systems,2015,23 (6):2034-2047.

[15]Li Yali,Li Yongming.Some properties of computation tree logic under possibility measure[J].Journal of Shanxi Normal University:Natural Science Edition,2013,41(6):6-12. [16]Gu Tianlong,Xu Zhoubo.Ordered binary decision diagram and application[M].Beijing:Science Press,2009.

附中文参考文献：

[4]林惠民,张文辉.模型检测:理论,方法与应用[J].电子学报,2002,30(12A):1907-1912.

[6]雷丽晖,段振华.一种基于扩展有限自动机验证组合Web服务的方法[J].软件学报,2007,18(12):2980-2990.

[11]李永明.模糊系统分析[M].北京:科学出版社,2005.

[12]王熙照.模糊测度和模糊积分及在分类技术中的应用[M].北京:科学出版社,2008.

[15]李亚利,李永明.可能性测度下计算树逻辑的若干性质[J].陕西师范大学学报:自然科学版,2013,41(6):6-12.

[16]古天龙,徐周波.有序二叉决策图及应用[M].北京:科学出版社,2009.

ZHAO Jie was born in 1990.He is an M.S.candidate at Shaanxi Normal University.His research interest is model checking.

赵杰（1990—），男，陕西宝鸡人，陕西师范大学硕士研究生，主要研究领域为模型检测。

LI Yongming was born in 1966.He received the Ph.D.degree from Sichuan University in 1996.Now he is a professor and Ph.D.supervisor at Shaanxi Normal University.His research interests include intelligent computing,fuzzy system analysis,quantum logic and quantum information,etc.

李永明（1966—），男，陕西大荔人，1996年于四川大学获得博士学位，1999年于西北工业大学博士后流动站出站，现为陕西师范大学教授、博士生导师，陕西师范大学图书馆馆长，主要研究领域为计算智能，模糊系统分析，量子计算与量子逻辑等。

Two Normal Forms Based on Generalized Possibilistic Computation Tree Logicƽ

ZHAO Jie,LI Yongming+
College of Computer Science,Shaanxi Normal University,Xi’an 710019,China

E-mail:liyongm@snnu.edu.cn

Normal form of computation tree logic(CTL)plays an important role in model checking.But the normal forms of computation tree logic based on generalized possibilistic measure have not been researched systematically. For improving the generalized possibilistic computation tree logic(GPoCTL)theory,according to existing generalized possibilistic computation tree logic theory and normal forms of classical computation tree logic,this paper defines two normal forms—positive normal form(PNF)and existential normal form(ENF)based on generalized possibilistic computation tree logic,and gives the corresponding language structure and semantic interpretation.Finally,using inductive method,this paper proves that any GPoCTL formula can write into a normal form in PNF or ENF respectively.

generalized possibility measure;computation tree logic;normal form;model checking

2015-06,Accepted 2015-08.

10.3778/j.issn.1673-9418.1507053

A

TP301.2

*The National Natural Science Foundation of China under Grant Nos.11271237,61228305(国家自然科学基金).

CNKI网络优先出版:2015-08-13,http://www.cnki.net/kcms/detail/11.5602.TP.20150813.1653.006.html

ZHAO Jie,LI Yongming.Two normal forms based on generalized possibilistic computation tree logic.Journal of Frontiers of Computer Science and Technology,2016,10(10)：1475-1481.