关于不同码长的多进制LDPC码误码率的研究
2016-10-28倪文丽何晶
倪文丽,何晶
(中国传媒大学 信息工程学院,北京 100024)
关于不同码长的多进制LDPC码误码率的研究
倪文丽,何晶
(中国传媒大学 信息工程学院,北京 100024)
本文构造了四进制的LDPC奇偶校验码,然后利用BP算法进行译码。有仿真表明,在同一个译码算法下,多进制LDPC码具有更为优异的性能,因此,本文是主要研究不同码长的多进制LDPC码,利用BP算法进行译码的情况下,通过MATLAB的仿真观察、研究不同码长误码率的情况。
多进制;LDPC码;BP算法;误码率
1 引言
LDPC码是由Gallager教授在1962年提出的,因当时无技术条件,从而LDPC码被人们忽略了一段时间,而最后一直等到1996年时,Mackay教授等人才“再发现”LDPC码。从此以后,因为LDPC码非常地接近香农极限,则被广泛地采用为有线和无线标准。
其实,二进制LDPC码是线性分组码的一种,而它的特别之处就是,LDPC码非常的稀疏,即非零个数小于零的个数。正是由于LDPC码的这种稀疏特性,才构造出了低复杂度、低误码率、高性能的校验矩阵。
BitFlipping算法译码,其实是一种概率译码算法,如果在译码过程中发生错误,校验节点和变量节点相关的校验方程不满足,,则会根据接收到信息和有关运算法则,改变一些比特值(0或1),改变之后,再继续判断是否满足校验方程或者达到译码的最大迭代次数。
本论文从以下几个方面谈起,第二部分就是谈非二进制LDPC码的校验矩阵的构造方法;BP译码算法写在第三部分;第四部分是在BP算法译码时,不同码长的多进制LDPC码的仿真结果;第五部分是不同码长误码率结论。
2 多进制校验矩阵的构造
二进制LDPC码已经被证明是接近香农的好码,其实多进制LDPC码可以看做是二进制在有限域上的扩展,也就是意味着,多进制LDPC码也是一种接近香农的好码。在有限域GF(q)(q=2p)中,多进制LDPC码的非零元素有q-1个元素组成,其定义在GF(q)上,在二进制的LDPC码就是非零元素只有1。但是,对于非二进制而言就是,例如本文中的四进制,非零元素就是1,2,3 。
如下图1所示,是构造出的一个四进制的校验矩阵:
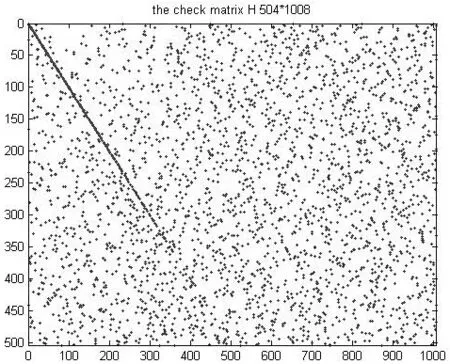
图1 校验矩阵H
3 BP算法
BP算法从Tanner图的角度来谈,如下图2所示,代表校验节点,代表变量节点,图中校验和各自对应的变量节点直接相连,与本身的节点无交集连线。当译码接收端每接收到一个码字时,然后再根据收到的可靠性消息,可获得每比特的可靠性程度。
然而,在Tanner图中,由于每一个校验节点都有与之相连的变量节点个数,根据这些变量节点的确定性信息,就可得出每一个校验节点的可靠性程度。根据校验节点的可靠性程度,又可以更新变量节点的信息,反复迭代这两类节点之间的可靠信息,如上所述的过程就是BP译码算法。
Tanner图如下图2所示:

图2 Tanner 图
BP算法是基于Tanner图的LDPC码的硬判决译码,其每一次迭代包括两个步骤:行向节点信息更新和列向节点信息更新。其译码的流程图如下图3所示。

图3 BP算法流程图
算法步骤如下:
(1).初始化
设信息位n取值为0和1的先验概率
(3.1)
(2).行向更新
第二步行向更新就是,由变量节点的概率信息得出校验节点的后验概率,对每一个校验概率m和对应的每一个nM(n),计算和。
定义
(3.2)
计算
(3.3)
则
(3.4)
图3BP算法流程图
(3).列向更新

(3.5)
更新概率值
(3.6)
其中αmn,αn为归一化参数。使得
(3.7)
(4).硬判决
将变量节点的后验概率,根据相对应的判决条件,做硬判决。
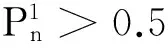
如果此时HTX=0,则表示译码成功,并且结束。X作为译码输出。否则又回到以上的这个步骤,直到满足以上HTX=0。还有最后一个步骤就是,如果译码迭代次数达到预设的最大次数,则也宣布译码结束。
4 不同码长译码仿真结果及结论
Gallager当时提出并且仿真出,二进制LDPC码随着码长的线性增加,并且进行迭代译码时,随之码字长度增加,而误码率则会降低。本文则是对不同码长四进制的LDPC码进行误码率差异比较的实验
仿真,对多进制不同码长的LDPC码,进行BP算法译码,如仿真结果所示,在性噪比相对大情况下,码长越长,则误码率就会明显降低。
仿真结果如下图4所示:

图4 不同码长的误码率比较
[1]RGGallager.Lowdensityparity-checkcodes[J].IRETrans,1992,8(1):21-28.
[2]DJCMacKayandRMNeal.NearShannonlimitperformanceoflowdensityparity-checkcodes[J].ElectronLett,1996,32:1645-1646.
[3]张延景,张立军.低密度奇偶校验码的构造方法研究[J].北京交通大学,信息网络与安全,2013.
[4]吴晓丽,葛建华.多进制LDPC码的编译码算法及结构研究[J].西安电子科技大学,通信与信息系统,2009.
[5]黄凡,刘卫忠.多进制LDPC码构造方法的研究[J].华中科技大学,微电子学与固体电子学,2011.
[6]刘东华,向良军.信道编码与MATLAB仿真[M].北京:电子工业出版社,2014,2.
(责任编辑:马玉凤)
TheBERResearchofnon-BinaryLDPCCodes
NIWen-li,HEJing
(InformationEngineeringSchool,CommunicationUniversityofChina,Beijing100024)
Thepaperconstructedfour-binaryLDPCcode,thenusetheBPalgorithmtodecodeit.
non-binary;LDPCcodes;BPalgorithm;BER
2016-04-18
倪文丽(1990-),女(汉族),陕西宝鸡人,中国传媒大学硕士研究生.E-mail:1520679144@qq.com
TN911.22
A
1673-4793(2016)03-0038-03
Thereisasimulation,whichshowsthatnon-binaryLDPCcodeshasbetterperformancethanbinaryLDPCcodesatthesamedecodingalgrithom.Therefore,thepapermainlyresearchthedifferentlengthsofthecodes,andusetheBPalgorithmtodecodethenon-binarycode,thenobservetheBERofthedifferentcodesbyMATLAB.
