多导体传输线分布参数的分析计算
2016-10-28杨莉逯贵祯
杨莉,逯贵祯
(中国传媒大学 信息工程学院,北京 100024)
多导体传输线分布参数的分析计算
杨莉,逯贵祯
(中国传媒大学 信息工程学院,北京 100024)
多导体传输线的串扰分析是信号完整性分析中经常遇到的问题。多导体传输线之间的串扰问题与传输线之间的分布参数存在密切联系,其分布参数分为分布电容矩阵和分布电感矩阵两个方面。本文采用有限元方法对由五条导线构成的一个多导体传输线结构进行建模,计算了该结构的单位长度分布电容矩阵和单位长度分布电感矩阵,分析了该结构中的串扰现象,通过与文献中结果对比,计算结果一致性很好,方法可行有效。
多导体传输线;电容矩阵;电感矩阵;有限元法;电磁兼容
1 引言
多导体传输线是大规模集成电路中的一个重要器件,它把电路中各种功能的器件连接在一起。多导体传输线之间的串扰问题是信号完整性分析中经常遇到的问题,它与传输线之间的分布参数矩阵密切相关,因此准确计算多导体传输线的分布参数对于减小传输线之间的串扰、改进传输线的设计非常重要。
多导体传输线的分布参数矩阵由分布电容矩阵和分布电感矩阵两部分组成,矩阵的计算方法包括解析计算和数值计算。与解析计算相比,数值计算适用于各种复杂结构,具有适用性强的特点。计算分布电容矩阵的数值计算方法主要有:有限元法[1-3]、矩量法[4,5]、谱域法[6]以及域分解法[7]等等。这些方法中,有限元法具有模拟各种不规则形状导线的优点,也更适用于非均匀复杂介质。在电感分布参数矩阵的数值计算中,目前通常的做法是先计算多导体传输线的电容矩阵,然后由真空中的电容矩阵和传播速度求解多导体传输线的电感矩阵。该计算方法中,电感矩阵的计算都是以电容矩阵的计算作为基础,与磁通密度没有关系,其不足之处在于不便于观察和研究传输线的电流分布以及传输线之间的近邻效应。
本文采用麦克斯韦静电场、静磁场方程的有限元方法,对放置在介质基板上由五条传输线构成的一个多导体传输线系统进行建模,从电容、电感的定义出发,计算了该结构的分布参数矩阵和特性阻抗,分析了其中的串扰现象。通过与文献[8]中得到的结果进行对比,可以看出结果接近一致,该方法在传输线分布参数矩阵的计算中精度较高,方法可行有效。
2 理论分析
对于理想导体的多导体传输线,电磁波沿导线传播TEM平面波。根据传输线理论,在TEM传播模式,电场与磁场只有垂直于传播方向的矢量场分量,并且满足静态场方程。麦克斯韦方程为:
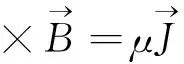
(1)

(2)
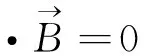
(3)
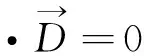
(4)
上述方程中,方程(1)和(3)用于分析分布参数电感矩阵;方程(2)和(4)用于分析分布参数电容矩阵。
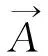
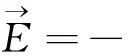
(5)

(6)
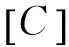
Q=C·V
(7)
用矩阵形式表示为:
(8)
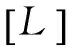
ψ=L·I
(9)
其中
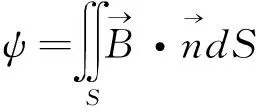
(10)
(9)式用矩阵形式表示为:
(11)
Y=L-1(LC)1/2
(12)
Z=Y-1
(13)
3 数值计算
采用文献[8]中的传输线模型,图1为其横截面结构示意图,其中每个传输线宽度5mm,厚度1mm,传输线间隔5mm,传输线基板厚度10mm,相对介电常数为11.7。
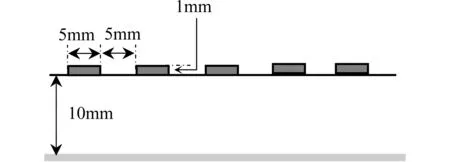
图1 传输线横截面结构示意图
3.1电容矩阵的计算
采用有限元方法计算传输线分布分布电容的具体过程为:为导线施加外部电压,利用静电场有限元方法计算出每个导线施加外部电压后产生的电场以及电荷,运用式(7)计算得到多导体传输线单位长度的分布电容矩阵。
图2为导体1施加1V电压后计算得到的传输线电势分布图,图3为电势分布等值图。
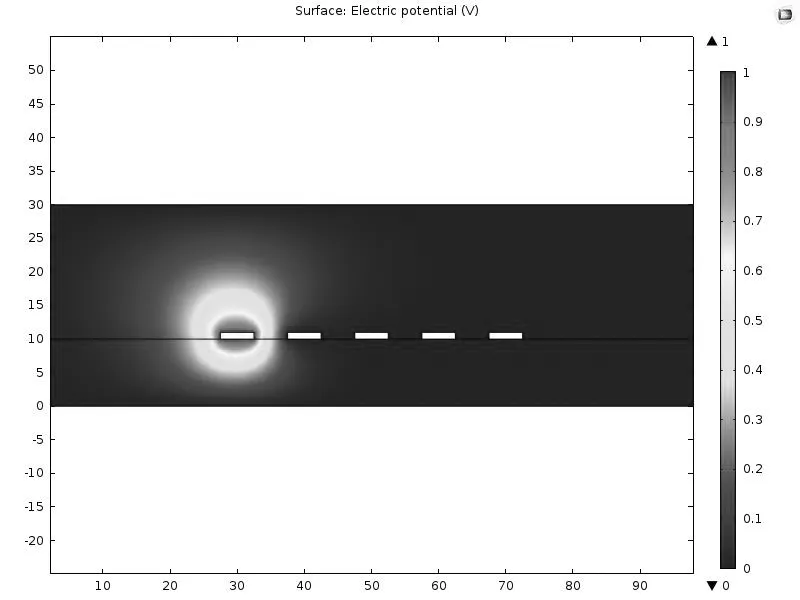
图2 传输线电势分布图
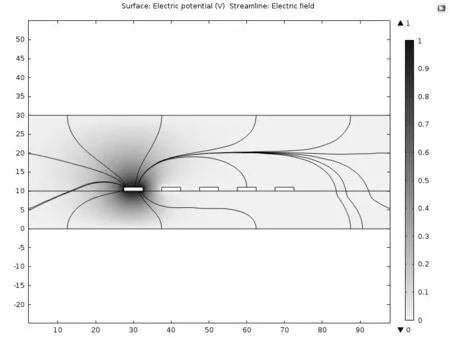
图3 电势分布等值图
利用有限元法计算得到的多导体传输线单位长度分布电容矩阵(单位:PF)为:

从电容的计算结果可以看出,由于电路结构的对称,所以该传输线的电容分布参数也具有对称性。其中导线1的自电容C11明显小于导线2的自电容C22和导线3的自电容C33。C11较小的原因是因为第一条导线位于传输线结构的最外边,它和地导体的平均距离要大于位于中间位置的传输线。中间三条导线中的每条导线由于其两边都有导线存在,因此它们到地的平均距离要相对小,对应的自电容就大。
从导线之间的互电容来看,对于导线1,互电容C12明显大于互电容C13、C14和C15的数值,这说明传输线的互耦电容主要来自相邻的导线。可以期望,传输线相邻导线的串扰影响是最大的。
3.2电感矩阵的计算
采用有限元方法计算传输线分布电感矩阵的具体过程为:首先利用有限元方法,计算出每个导线施加外部电流后产生的磁场密度,利用式(10)求出对应的磁通,然后运用式(11)计算多导体传输线的电感矩阵。
图4为导体1施加1A电流后,计算得到的传输线磁通密度分布,图5为其磁通密度分布的等值图。
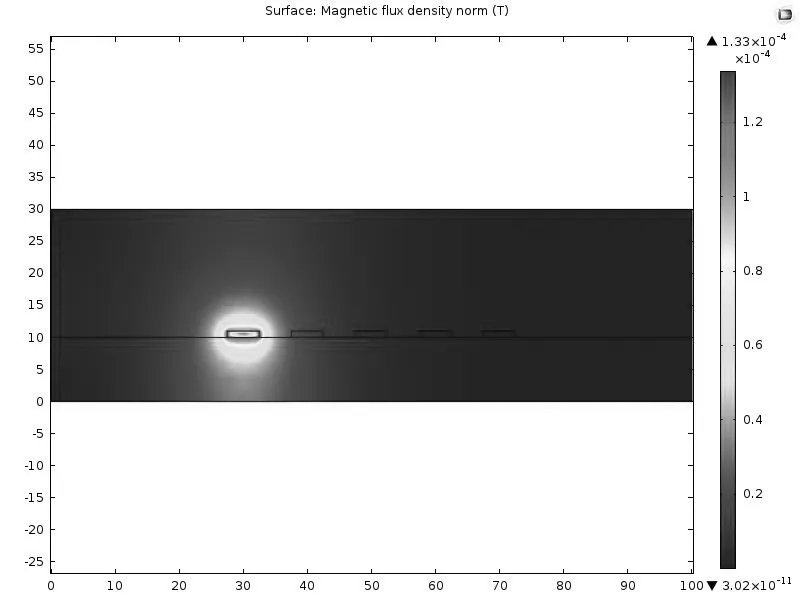
图4 传输线磁通密度分布图
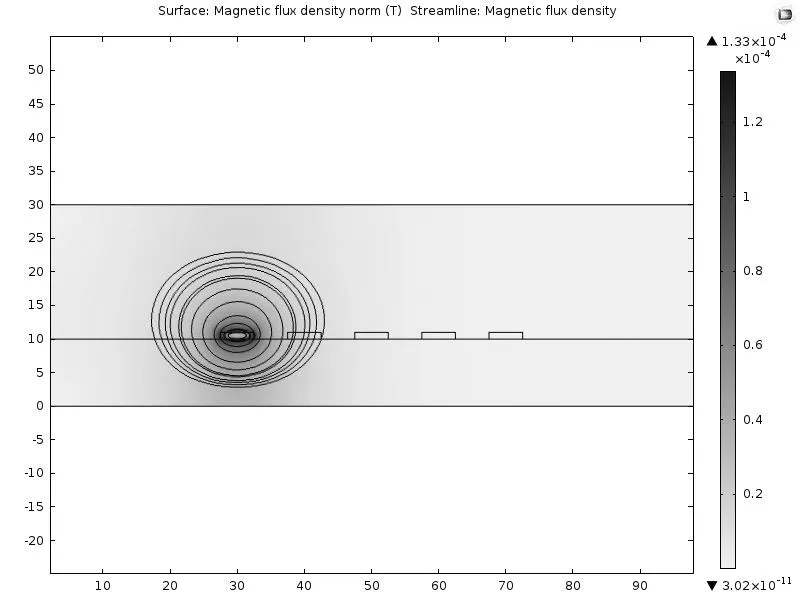
图5 磁通密度分布等值图
计算得到多导体传输线单位长度的分布电感矩阵(单位:nH)为:
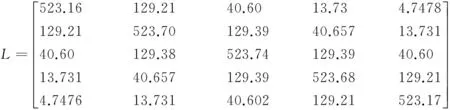
由电感矩阵可以看出,处于中心位置的导线自感要略大于边缘位置的导线自感。导线之间的互感也遵从相邻导线之间的互感要大于非相邻互感的规律。因此对于多导体传输线来说,相邻导线之间的串扰影响要远大于非相邻导线之间的串扰。
3.3特性阻抗的计算
由计算得到的分布电容参数和分布电感参数,利用式(12)、(13)计算得到图1所示多导体传输线的特性阻抗矩阵(单位:)为:

文献[8]中的得到的电容矩阵(单位:PF)、电感矩阵(单位:nH)分别为:



4 结论
多导体传输线之间的互扰问题与传输线的分布参数矩阵密切相关。多导体传输线的分布电感矩阵和分布电容矩阵是研究多导体传输线特性的基础。本文采用有限元方法,对放置在介质基板上由五条传输线构成的一个多导体传输线结构进行分析,计算了该结构单位长度的分布电容矩阵和分布电感矩阵,求解了它的特性阻抗,并与文献中结论进行了比较,可以看出计算结果接近一致。有限元方法在传输线分布参数矩阵的计算中精度较高,方法可行有效。
[1]Musa S M,Sadiku M N O.Analysis of multiconductor Quasi-TEM transmission lines and multimode waveguides[J].InternationalJournalofEngineeringResearchandDevelopment,2014,10(3):87-93.
[2]Musa S M,Sadiku M N O,Obiomon P H.Integrated circuit interconnect lines on lossy silicon substrate with finite element method[J].JournalofEngineeringResearchandApplications,2014,4(1):243-247.
[3]Musa S M,Sadiku M N O,Emam A Z.Finite element analysis of integrated circuit interconnect lines on lossy silicon substrate[C]//Proceedings of the2011 COMSOL Conference in Boston,2011.
[4]Cao W,Harrington R F,Mautz J R.Multiconductor transmission lines in multilayered dielectric media[J].IEEETransmissionsonMicrowaveTheoryandTechniques,1984,32(4):439-450.
[5]Cao W,Harrington R F.Computation of the parameters of multiconductor transmission lines in two dielectric layers above a ground plane[R].Springfield:Department Electrical Computer Eng,Syracuse University,Rep,1982.
[6]Plaza G,Mesa F,Horno M.Quick computation of [C],[L],[G],and [R] matrices of multiconductor and multilayered transmission systems[J].IEEETransmissionsonMicrowaveTheoryandTechniques,1995,43(7):1623-1626.
[7]Liu S J,Zhu H Q.An efficient algorithm for the parameter extraction of multiconductor transmission lines in multilayer dielectric media[C]//Proceeding of IEEE Antennas and Propagation Society International Symposium,2005:228-231.
[8]You Y,Palusinski O A,Szidarovszky F.New matrix for calculating xiagonallymatched impedance of packaging interconnecting lines[J].IEEETransactionsonMicrowaveTheoryandTechniques,1999,47(6):798-801.
(责任编辑:马玉凤)
Calculating Distributed Parameters of Multi-Conductor Transmission Lines
YANG Li,LU Gui-zhen
(Information Engineering School,Communication University of China,Being 100024)
The Crosstalk analysis of multi-conductor transmission lines is critical to the signal integrity.It is closely related to distributed parameters of multi-conductor transmission lines.In this paper,the finite element method is used to calculate the distributed capacitance matrix and the distributed inductancematrix of the multi-conductor transmission lines,whichis formed with five conductors in a single-layered dielectric medium.The results are compared with the work of the previous literatures.They are in good agreement,and the method is feasible.
multi-conductor transmission lines;capacitance matrix;inductance matrix;the finite element method;electromagnetic compatibility
2016-03-04
杨莉(1977-),女(汉族),甘肃省定西市人,中国传媒大学信息工程学院讲师.E-mail:onion@cuc.edu.cn
TM153
A
1673-4793(2016)03-0017-05
