一种解Dantzig-Selector模型的快速分解算法

张　乾，何　岸，何洪津

(杭州电子科技大学理学院，浙江 杭州 310018)



一种解Dantzig-Selector模型的快速分解算法

张乾，何岸，何洪津

(杭州电子科技大学理学院，浙江 杭州 310018)

基于增广拉格朗日法提出了一种快速分解算法求解Dantzig-Selector模型.与经典的乘子交替方向法相比，新算法的每个子问题都具有更简单易行的迭代格式.通过测试两种不同类型的随机数据，相应的数值计算结果表明，算法在CPU运行时间方面有较明显的优势.

Dantzig-Selector模型；增广拉格朗日方法；乘子交替方向法；分解算法

0　引　言

线性回归是一类非常经典的数学模型，它在信号处理、机器学习以及统计学习中有着极其广泛的应用.由于压缩感知理论[1]的提出，寻找欠定线性回归模型的稀疏解成为近年来最热门的研究课题之一.然而，直接寻找满足线性方程组的稀疏解是一个NP-难问题.为此，研究者提出了一系列凸松弛优化模型，例如基追踪模型[2]和LASSO模型[3].2007年，Candes和Tao针对超欠定线性方程组问题进一步提出了更稳健的Dantzig-Selector模型[4].与LASSO模型相比，Dantzig-Selector模型结构更为复杂，从而给模型的求解增加了很大的困难.如何设计简单高效的算法求解该模型是极具挑战性的研究课题之一.本文首先通过引入两个新的辅助变量，将Dantzig-Selector模型等价转化为弱分离的优化问题.然后，基于增广拉格朗日方法，充分利用新模型的结构特点设计出一种快速、可行的分解算法，使得算法的子问题都具有显式表达式.相比已有的分裂算法，本文算法在CPU运行时间上有较明显的优势.

1　问题描述

经典的线性回归问题可刻画为：

y=Xβ+ε.

(1)

式中，β∈Rp是未知的回归系数，X∈Rn×p是一个有界的线性算子(或设计矩阵)，y∈Rn是带噪音的观测向量，ε是服从正态分布N(0,σ2I)的可加噪音.为了克服式(1)的病态性给模型求解过程带来的不稳定性，通常在最小二乘模型上引入Tikhonov正则化技术.但是，当β具有稀疏结构时，且当式(1)是一个超欠定线性系统，即n≪p时，传统的最小二乘模型及Tikhonov正则化得到的解无法满足需求.2007年，Candes和Tao在LASSO模型的基础上提出了Dantzig-Selector模型[4]：

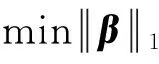
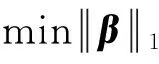
(3)

上述模型是标准的带线性约束的凸优化模型，而增广拉格朗日函数是求解此类问题的经典方法之一.但是，直接使用增广拉格朗日方法会使得子问题变量耦合在一起，不利于算法的实现.因此，根据目标函数的可分离性，文献[6]利用乘子交替方向法进行求解，且取得了良好的数值效果.美中不足之处是，直接利用乘子交替方向法求解，其关于β部分的子问题没有显式表达式，这给算法的实现增加了一定难度.随后，文献[7]巧妙地将与β有关的子问题进行线性化，提高了乘子交替方向法的可操作性，也在一定程度上减少了算法的计算时间.但他们的方法要求估计一个矩阵的谱半径，这也并非一件易事.基于上述原因，本文寻求一种新的简单易行的算法.

2　变量分离算法

针对模型(3)，引入增广拉格朗日函数：

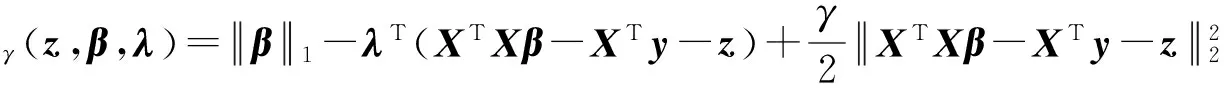
(4)

式中，γ>0是罚参数，λ表示拉格朗日乘子.给定(βk,λk),文献[5]中的乘子交替方向法的迭代格式可描述为：

(5)

(6)

λk+1=λk-γ(XTXβk+1-XTy-zk+1)

(7)

显然，乘子交替方向法主要的任务就是求解子问题(5)和问题(6).由于子问题(5)可以显式求解，子问题(6)的求解直接决定了算法的有效性.但由于XTX在通常情况下并不是一个单位矩阵，因此，式(6)并没有显式解，此时必须借助一些迭代算法进行近似求解，这为算法的实现增加了较大的难度.基于乘子交替方向法的思想，下面提出一种新的分解算法，使得新算法所有子问题具有显式迭代式.

为了简化数学符号，记A∶=XTX和b∶=XTy.通过引入辅助变量x和z，模型(2)可转化为弱分离优化问题：

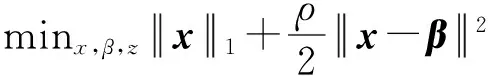
(8)

式中，ρ>0是一个惩罚因子.针对模型(8)，相应的增广拉格朗日函数为：

(9)

式中，λ和γ分别代表拉格朗日乘子和罚参数.根据乘子交替方向法的Gauss-Seidel迭代思想，给定(xk,βk,λk)，分别对式(9)中的变量进行交替求解，即得如下迭代格式：

(10)

(11)

(12)

λk+1=λk-γ(Aβk+1-b-zk+1)

(13)

类似迭代格式(5)～(7),上述方法的主要工作量集中在子问题(10)～(12).下文中，本文主要讨论式(10)～(12)的具体表达式.

首先，关于变量z的子问题(10)归结为：

(14)

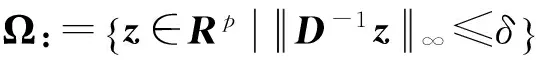
(15)

式中，diag(D)表示由D矩阵对角元素构成的列向量.

(16)

最后，将(zk+1,xk+1)代入(12)式，简化关于β的子问题为：

(17)

(18)

由上述分析可见，本文新提出的算法其每个子问题都能显式求解，这相比文献[5]中的乘子交替方向法更容易实现.当矩阵A具有某些特殊结构时，可以借助一些快速矩阵求逆方法对式(18)进行求解(例如：快速傅立叶变换).当矩阵A规模较大且无特殊结构时，(γATA+ρI)的逆矩阵求解则会比较耗时.此时，建议采用快速、成熟的共轭梯度法[8]进行近似求解，即：

βk+1=βk-αkgk

(19)

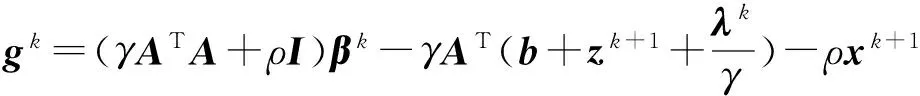
当处理(18)的病态情形时，在共轭梯度法中引入预处理迭代技术增加算法的稳定性和可靠性，这也是新算法的一个潜在优势.综上分析，本文的分解算法过程可描述如下：

新的快速分解算法解Dantzig-Selector模型的算法步骤如下：

1) 输入初始迭代点(x0,β0,λ0)，选择参数δ,ρ,γ>0；

2) 通过式(15)更新zk+1；

3) 通过式(16)更新xk+1；

4) 通过式(18)或(19)更新βk+1；

5) 通过式(13)更新λk+1.

3　数值实验

本节对新提出的算法进行数值模拟来检验算法的优劣.考虑到β子问题的计算方式，新算法分为式(18)的精确计算(简记为“New-accurate”)和式(19)的一步迭代近似计算(简记为“New-one”).同时，将新算法与文献[5]中的乘子交替方向法(简记为“ADMM”)进行比较.所有算法都用MATLAB进行编程实现，其中文献[5]的ADMM算法程序由该文作者提供.

类似文献[4]的测试情况，本节仍考虑两种类型的系数矩阵X：单位列向量系数矩阵和行正交系数矩阵.实验中设定初始值迭代点为(x0,β0,λ0)=(0,0,0).新算法(New-one和New-accurate)迭代的停止条件设定为：

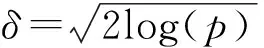
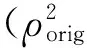
表1和表2的数值结果表明New-one算法和ADMM在得到质量相当的近似解时，New-one所需的CPU运行时间比后者要少，这进一步从数值上验证了本文新方法在求解子问题方面的优势.若直接使用式(18)更新βk+1，则需要计算矩阵的逆.一般情况下，计算矩阵的逆代价比较高，从New-accurate算法的数值结果也表明其CPU运行时间较长.同时，本文处理的问题非常病态，故矩阵直接求逆的迭代方式导致计算结果不如另外两种方式，因而进一步说明式(19)的重要性.但是，在矩阵维数比较低时，New-accurate的近似解效果还是令人满意，从某种程度上说，当矩阵X具有某种特殊结构时，或许可采用快速傅立叶变换实现高精度的快速求解.

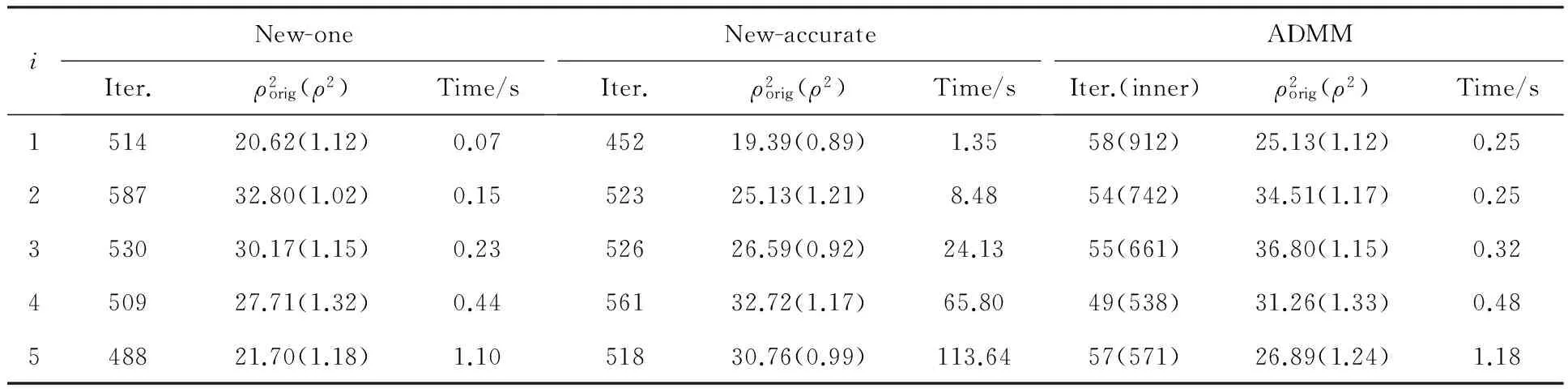
表1　当X为单位列向量矩阵时，3种算法数值结果

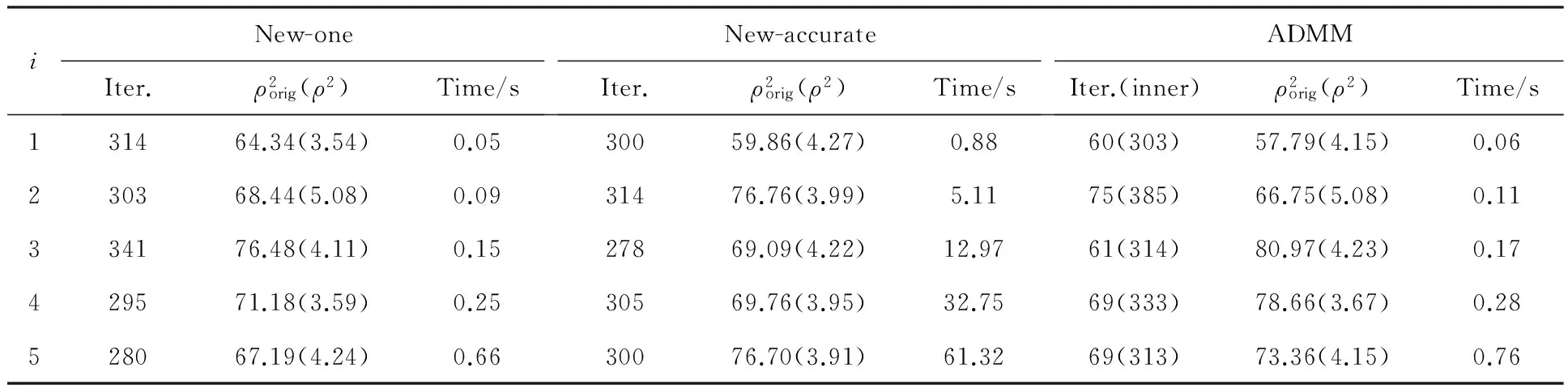
表2　当X为行正交矩阵时，3种算法数值结果

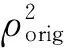
图1　X为行正交矩阵时的迭代次数比较

图2　X为单位列向量矩阵时的迭代次数比较

图3　X为行正交矩阵时的计算误差比较

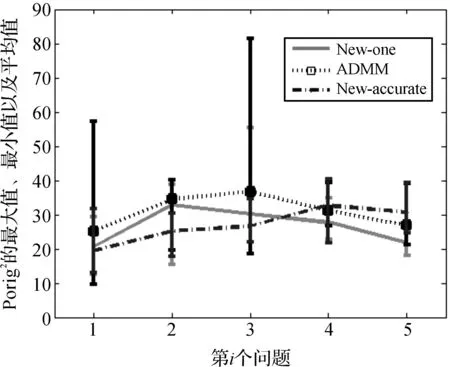
图4　X为单位列向量矩阵时的计算误差的比较

图5和图6分别画出了当(n,p,s)=(72,256,8)时两种不同类型系数矩阵对应的数值解情况.两幅图可看出New-one恢复出来的数值解令人满意.

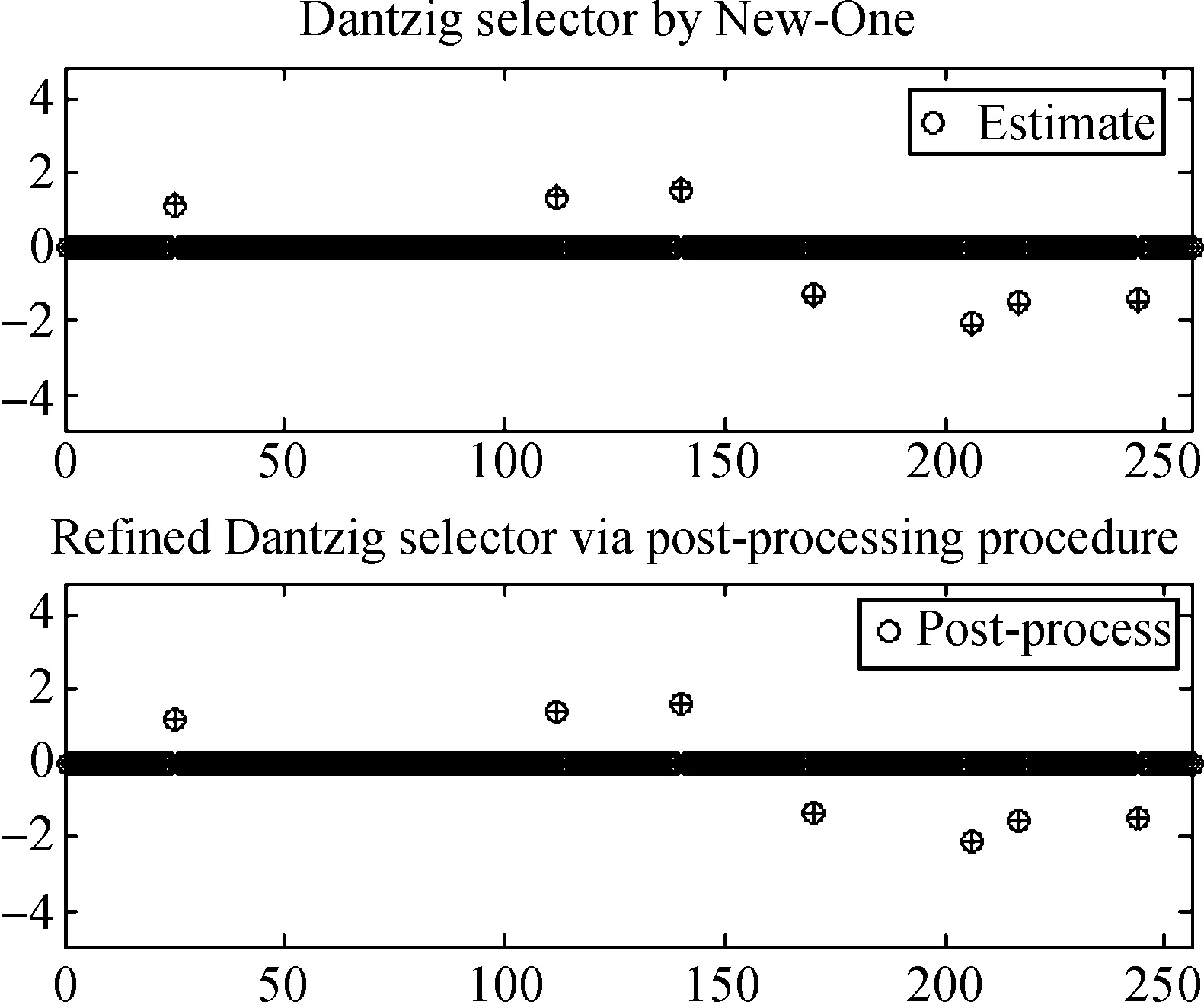
图5　X为行正交矩阵时的近似解

图6　X为单位列向量矩阵时的近似解

4　结束语

鉴于直接使用乘子交替方向法求解Dantzig-Selector模型时子问题不具有显式迭代格式的缺陷，本文引入一种新的模型刻画技巧，提出了一种子问题简单易行的分解算法.通过测试两种不同类型的随机数据，初步的数值结果表明新算法在CPU运行时间方面有较明显的优势.

[1]DONOHO D L.Compressed sensing[J]. Information Theory, IEEE Transactions on,2006,52(4):1289-1306.

[2]CHEN S S, DONOHO D L, SAUNDERS M A. Automatic decomposition by basis pursuit[J]. SIAM Journal on Scientific Computing,1998,20(1):33-61.

[3]TIBSHIRANI R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society B,1996,58(1):267-288.

[4]CANDES E, TAO T. The Dantzig selector: statistical estimation when p is much larger than n[J]. Annals of Statistics,2007,35(6):2313-2351.

[5]LU Z S, PONG T K, ZHANG Y. An alternating direction method for finding Dantzig selectors[J]. Computational Statistics & Data Analysis,2012,56(12):4037-4046.

[6]GABAY D, MERCIER B. A dual algorithm for the solution of nonlinear variational problems via finite element approximations[J]. Computers & Mathematics with Applications,1976,2(1):16-40.

[7]WANG X, YUAN X. The linearized alternating direction method of multipliers for Dantzig selector[J]. SIAM Journal on Scientific Computing,2012,34(5):A2792-A2811.

[8]袁亚湘,孙文瑜.最优化理论与方法[M].北京:科学出版社,1996:186-194.

A Fast Decomposition Algorithm for Finding Dantzig-Selectors

ZHANG Qian, HE An, HE Hongjin

(SchoolofScience,HangzhouDianziUniversity,HangzhouZhejiang310018,China)

Based on the augmented Lagrangian method, this paper introduces a fast decomposition algorithm for solving the Dantzig selector model. Comparing with the classical alternating direction method of multipliers, all subproblems of the proposed algorithm have closed-form solutions so that the new algorithm is easily implementable in practice. Finally some preliminary numerical results show that our new algorithm has superiority in terms of taking less CPU time by testing two types of synthetic data sets.

Dantzig-Selector model; augmented Lagrangian method; alternating direction method of multipliers; decomposition method

10.13954/j.cnki.hdu.2016.01.020

2015-06-22

浙江省自然科学基金重点资助项目(LZ14A010003)；浙江省大学生新苗人才计划资助项目(2015R407038)

张乾(1993-)，女，河南周口人，在读本科生，数值优化和变分不等式.通信作者：何洪津讲师，E-mail: hehjmath@hdu.edu.cn.

O221.2

A

1001-9146(2016)01-0097-06