一类网络控制系统的不匹配控制器设计

许嘉伟，周绍生

(杭州电子科技大学自动化学院，浙江 杭州 310018)



一类网络控制系统的不匹配控制器设计

许嘉伟，周绍生

(杭州电子科技大学自动化学院，浙江 杭州 310018)

主要研究了一类非线性网络控制系统的控制设计问题，推导出一种能使被控系统稳定的不匹配控制器设计方法.通过线性T-S网络模型对这类系统进行描述，并且在系统建模时考虑网络诱导时延和数据丢失等情况对模型的作用.基于Lyapunov-Krasovskii泛函的方法，并引入松弛矩阵和矩阵不等式，得出一个使被控系统稳定的充分条件.仿真实例说明了该方法具有良好的控制作用.

T-S模型；网络控制系统；前提不匹配

0　引　言

随着网络和计算机技术的飞速发展，以及人们对工业生产过程中各种要求的提高，网络控制系统越来越受人们关注.它相比于传统的点对点控制具有低成本、高效率、易安装和易维护，以及占地少等优势.但网络诱导时延、数据包丢失、数据包乱序等不理想的网络状况对系统的稳定性有很大的影响.近年来，学者们已经对网络控制系统的稳定分析和控制设计等问题进行了大量的工作.其中有很多是针对线性网络控制系统的研究[1-2]，也有少量的关于非线性网络控制系统的研究.例如，文献[3]研究了基于T-S模型的非线性网络控制的控制设计问题，提出了一种迭代的控制器设计方法.文献[4]研究了基于T-S模型的非线性网络控制系统的H∞控制问题，通过利用隶属函数的异步误差是有界这一特点和一些自由权矩阵，提出了一种新的模糊控制器设计方法.文献[5]提出了一种基依赖的Lyapunov-Krasovskii方程，解决了一类具有不确定性的离散模糊系统的鲁棒控制问题.前人对网络控制系统的研究大多是基于前提变量匹配的控制器设计方法，相比于现有的研究，本文提出了一种前提变量不匹配的控制器设计方法，使非线性网络控制系统渐近稳定.

1　系统描述

本文考虑的非线性网络控制系统由一个具有非线性特点的被控对象，通过网络连接的模糊控制器，和带有零阶保持器的执行机构组成.本文研究的非线性网络系统表示为T-S形式，其模糊规则如下：

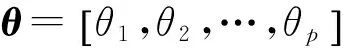
(1)

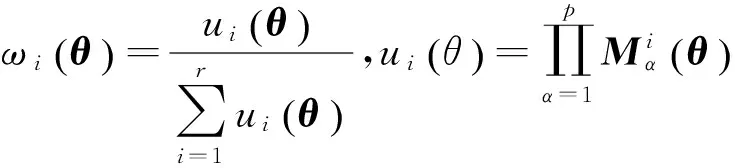
首先，在网络控制系统中，为了便于系统描述，需要做如下假设：传感器部分是时钟驱动的，数据包是单包传输，并且每个传输的数据包都具有一个时间标识.控制器部分是事件驱动的，当传输信号到达时就会被触发.执行器部分也是事件驱动的，它带有一个逻辑零阶保持器，这个零阶保持器只保持最新的数据包.

其次，网络控制的过程是在传感器采样后，将采样得到的前件变量θ(kh)和反馈的状态x(kh)的值先通过网络传输到模糊控制器产生控制信号u(bkh)，再通过网络传输控制信号u(ikh)到达执行器.

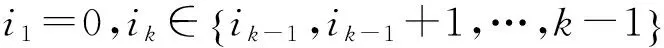
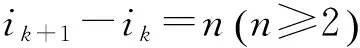
网络诱发时延τk可以表示为τk=τsc+τca.其中，τsc为传感器到控制器的时延，τca为控制器到执行器的时滞，至于计算本身的时滞τc，与前两种时滞相比十分小，因此可以忽略不计.

(2)

根据文献[7]中的描述，网络诱导时延和连续丢包数是有上界的，因此可以定义系统的输入时滞：

(3)

式中：τ1为时滞下界，τ2为时滞上界.把式(3)经变换后带入式(2)，得到如下的控制器：

(4)

将控制器(4)代入系统(1)，得到的闭环系统方程可以表示为：

(5)

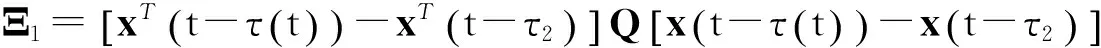
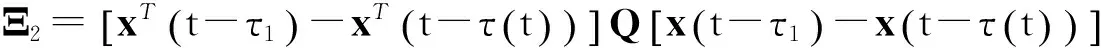
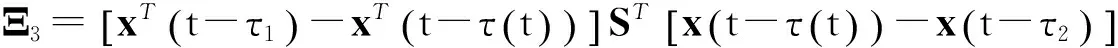
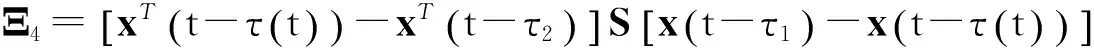
2　主要结果

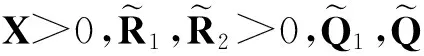
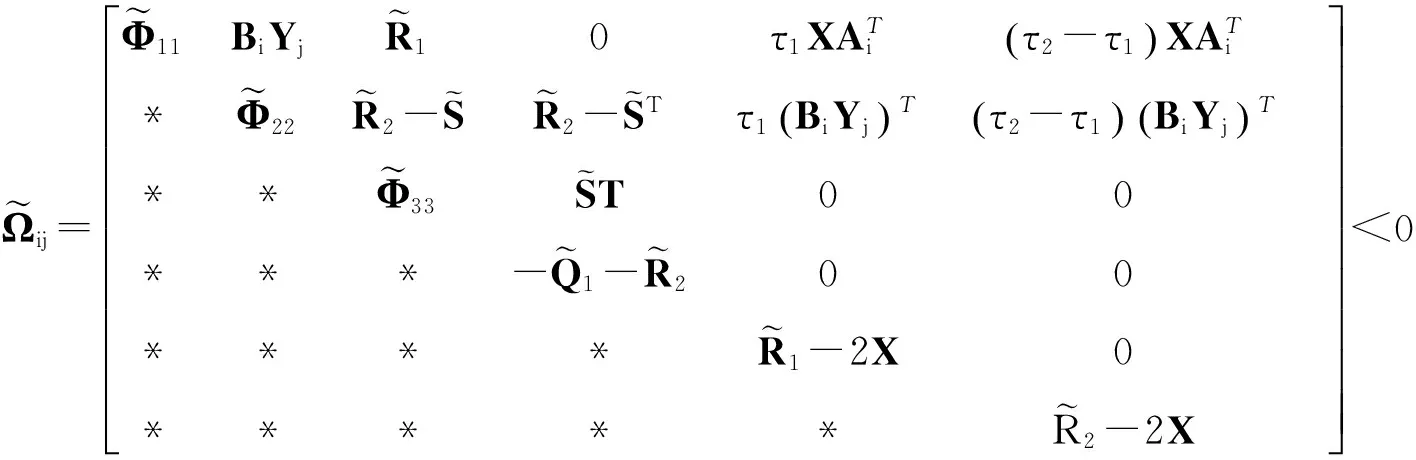
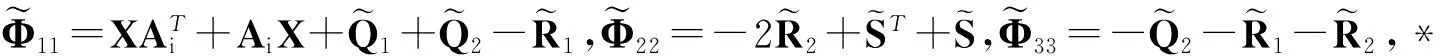
证明考虑如下形式的Lyapunov-Krasovskii泛函

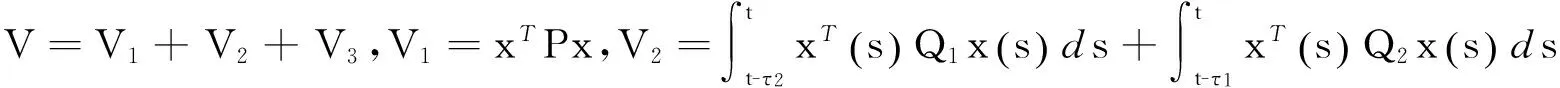
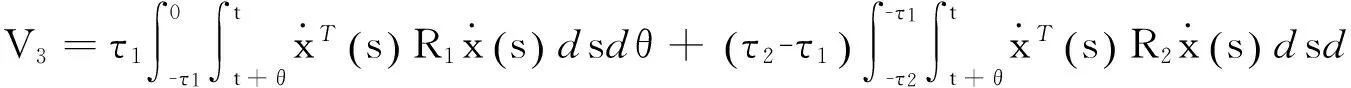
根据引理1，那么V的导数

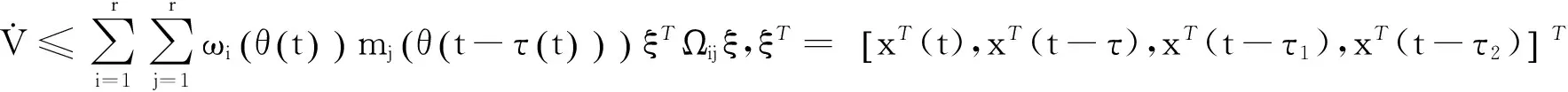
(6)

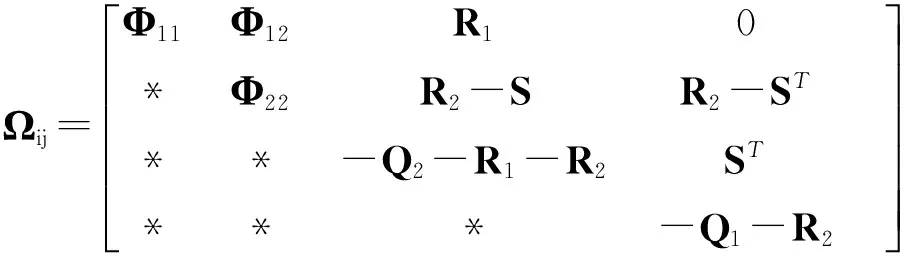
对于上述矩阵Ωij，利用舒尔补引理，可以变换得到矩阵

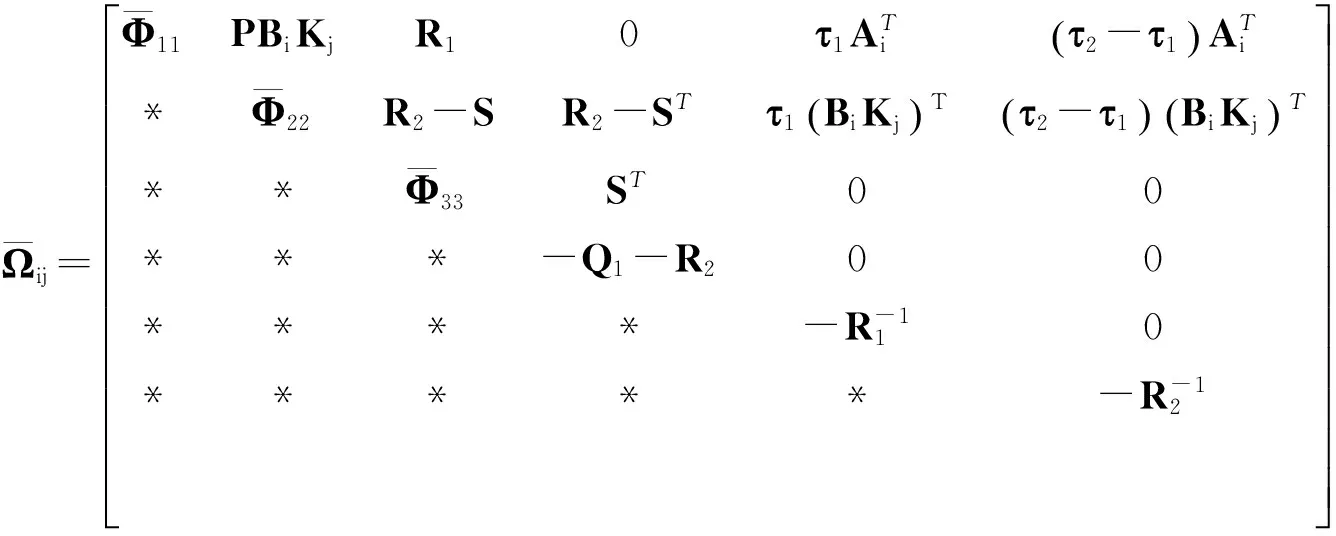
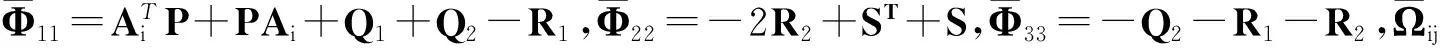
综上，当式(6)及定理1中的条件能满足时，系统(5)能够渐近稳定，定理1证毕.

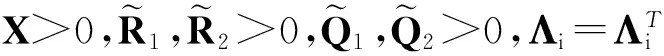
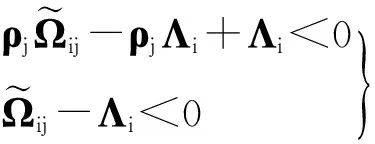
证明由定理1可知，式(6)成立是系统(8)稳定的充分条件，即

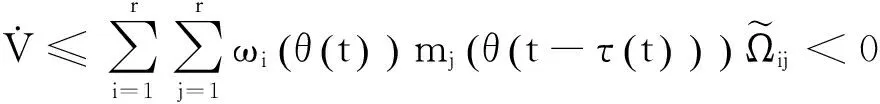
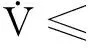
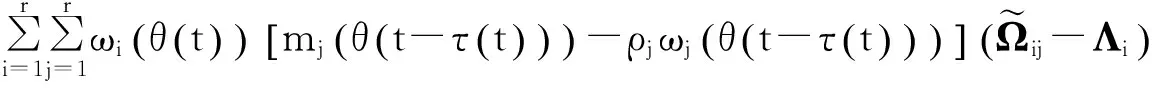
(7)

3　数值实例

考虑如下非线性的弹簧-质点系统：

(8)

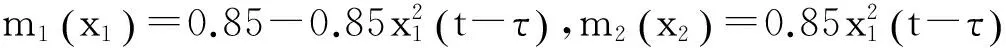
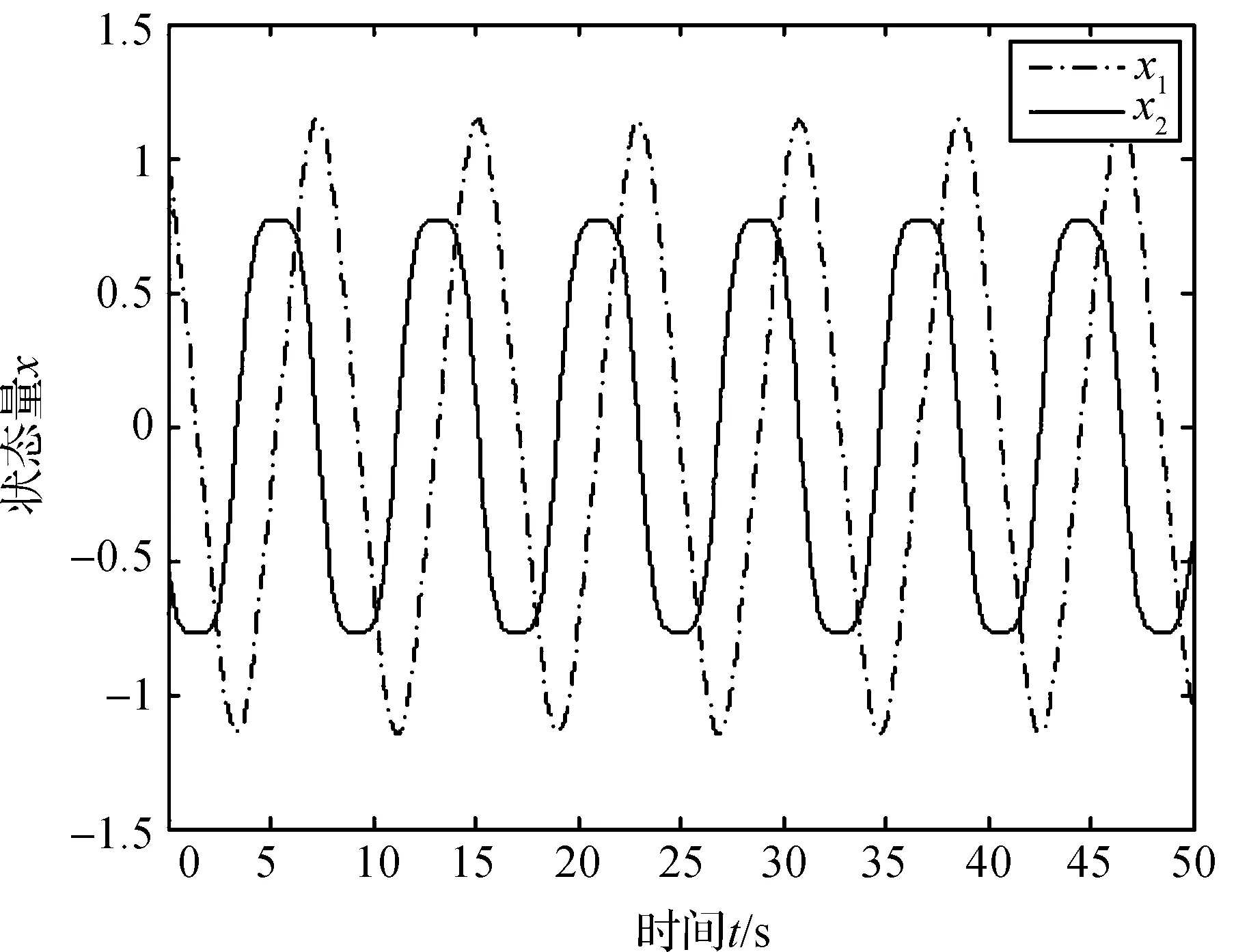
图1　系统开环状态响应曲线

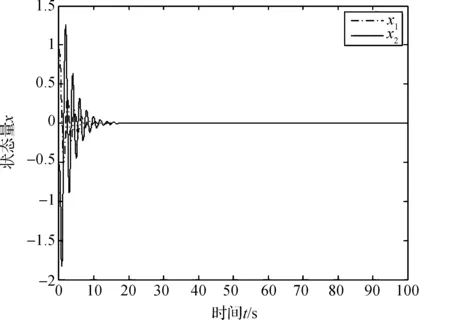
图2　系统闭环状态响应曲线

由图1可知，系统开环时，状态量一直震荡，系统不稳定，图2表明在加入控制后20s之内，系统趋于稳定.

4　结束语

本文主要对基于T-S系统的网络控制系统设计了不匹配的控制器，该控制器设计方法在隶属度选择上具有更大的自由度.在设计过程中本文采用了一些松弛矩阵和矩阵不等式的技巧，能使被控系统稳定.最后通过仿真例子，验证了所设计方法的有效性.

[1]ZHIVOGLYADOVPV,MIDDLETONRH.Networkedcontroldesignforlinearsystems[J].Automatica,2003,39(4):743-750.

[2]LIUY,LIM.Animproveddelay-dependentstabilitycriterionofnetworkedcontrolsystems[J].JournaloftheFranklinInstitute,2014,351(3):1540-1552.

[3]JIANGX,HANQL.Ondesigningfuzzycontrollersforaclassofnonlinearnetworkedcontrolsystems[J].FuzzySystems,IEEETransactionson,2008,16(4):1050-1060.

[4]ZHANGD,HANQL.H∞controldesignfornetwork-basedTSfuzzysystemswithasynchronousconstraintsonmembershipfunctions[C]//IECON2011-37thAnnualConferenceonIEEEIndustrialElectronicsSociety.Melbourne:IEEE,2011:2584-2589.

[5]ZHOUS,LIT.Robuststabilizationfordelayeddiscrete-timefuzzysystemsviabasis-dependentLyapunov-Krasovskiifunction[J].FuzzySetsandsystems,2005,151(1):139-153.

[6]LAMHK,NARIMANIM.Stabilityanalysisandperformancedesignforfuzzy-model-basedcontrolsystemunderimperfectpremisematching[J].FuzzySystems,IEEETransactionson,2009,17(4):949-961.

[7]XIONGJ,LAMJ.StabilizationofnetworkedcontrolsystemswithalogicZOH[J].AutomaticControl,IEEETransactionson,2009,54(2):358-363.

[8]PENGC,FEIMR.AnimprovedresultonthestabilityofuncertainT-Sfuzzysystemswithintervaltime-varyingdelay[J].FuzzySetsandSystems,2013,212:97-109.

AControlDesignforaClassofNetworkedControlSystemsunder

ImperfectPremiseMatching

XUJiawei,ZHOUShaosheng

(School of Automation, Hangzhou Dianzi University, Hangzhou Zhejiang 310018, China)

Thispaperisconcernedwithacontroldesignmethodforaclassofnonlinearnetworkedsystems.AT-Sfuzzymodelisusedtoapproximatethenonlinearnetworkedcontrolsystems(NCSs),thenetwork-inducedelaysandpacketdropoutsaretakenintoaccount.ByconstructingaLyapunov-Krasovskiifunctional,usingsomematrixinequalitiesandsomeslackmatrices,anewcriteriaonthedesignofafuzzycontrollerunderimperfectpremisematching(IPM)isderived.Simulationexamplehasbeengiventoillustratetheeffectivenessoftheproposedapproach.

T-Smodel;networkedcontrolsystems;imperfectpremisematching

10.13954/j.cnki.hdu.2016.01.010

2015-06-23

国家自然科学基金资助项目(61273093)；浙江省自然科学基金资助项目(LZ12F03001)

许嘉伟(1992-),男,浙江东阳人,在读研究生,先进控制理论.通信作者:周绍生教授,E-mail:sszhou@hdu.edu.cn.

TP273

A

1001-9146(2016)01-0046-05