燃油管路系统振动特性有限元模拟技术

赵伟志，陈志英

（北京航空航天大学能源与动力工程学院，北京100191）

燃油管路系统振动特性有限元模拟技术

赵伟志，陈志英

（北京航空航天大学能源与动力工程学院，北京100191）

航空发动机燃油管主要用于提供燃油，属于复杂3维管路系统。为了更好地分析管路系统的振动特性，以双路总管燃油管路系统为例，结合其管路繁多、连接结构多样、支撑结构特殊、管内充液等特点，系统研究了各部件的有限元模拟方法。考虑到支撑刚度对管路系统振动特性有较大影响，采用有限元静力分析对其进行了求解。结合以上不同部件的分析方法，建立起系统的振动有限元模型。对该管路系统进行模态分析，得到系统固有频率变化规律及具有分簇特点的振动模态；对系统进行共振评估，认为副燃油分管最有可能发生共振，提出了振动优化的合理建议。

燃油管路；振动特性；支撑刚度；有限元；航空发动机

0　引言

航空发动机燃油管路主要用于输送燃油，由管路组件及其连接件、密封件、支架、卡箍等组成，作为发动机外部管路的1支，是发动机附件系统的重要组成部分。燃油管的结构设计及特性与发动机的性能紧密相关，对飞机的稳定工作也有着重要影响［1］。燃油管路系统属于复杂的3维管路系统，因此管路故障极易发生［2］，其原因有加工、装配、温度和振动等诸多因素，而振动问题是其中最主要的根源之一［3］。因此，研究系统的动力学特性对于管路敷设、振动控制等具有指导意义。

在管路振动问题的相关研究中，有限元方法已经得到了广泛应用。Sreejith［4］考虑流固耦合振动，采用有限元法研究了核工业管路中流速对系统振动频率的影响；杨莹［5］采用壳单元有限元法研究了管内流体质量、压力、温度、管路形状等对管路固有频率的影响；刘伟等［6］采用有限元法研究了卡箍位置对管路振动频率的影响并提出了优化设计方案；贾志刚［7］研究了不同结构模式管路的振动特性以及调频方法；黄益民［8］等针对输流管道分析评估了不同支撑刚度对其动力学特性完整性影响。目前，采用有限元方法研究管路振动问题一般针对基本管路或局部管路，对空间复杂的燃油管路系统的研究较少。

双路燃油管路系统的管路结构复杂、数量众多且连接形式多样，建立系统的有限元模型需要综合考虑单元类型及数量、支撑结构和连接结构的力学模型、支撑刚度的求解以及燃油的流固耦合等，本文详细阐述了燃油管路系统的有限元模拟技术，并分析系统的振动特性。

1　典型燃油管路系统的结构特点

燃油管路系统如图1所示。该系统具有主、副2路燃油管路。环形的为主、副燃油总管，分2段，通过管接头连接；总管上的分支部分为燃油分管，分管与总管之间通过3通管接头连接，分管另一端通过管接头连接燃油喷嘴。主、副燃油总管之间通过带有支架的双管卡箍连接，支架将管路系统固定到发动机的机匣上。

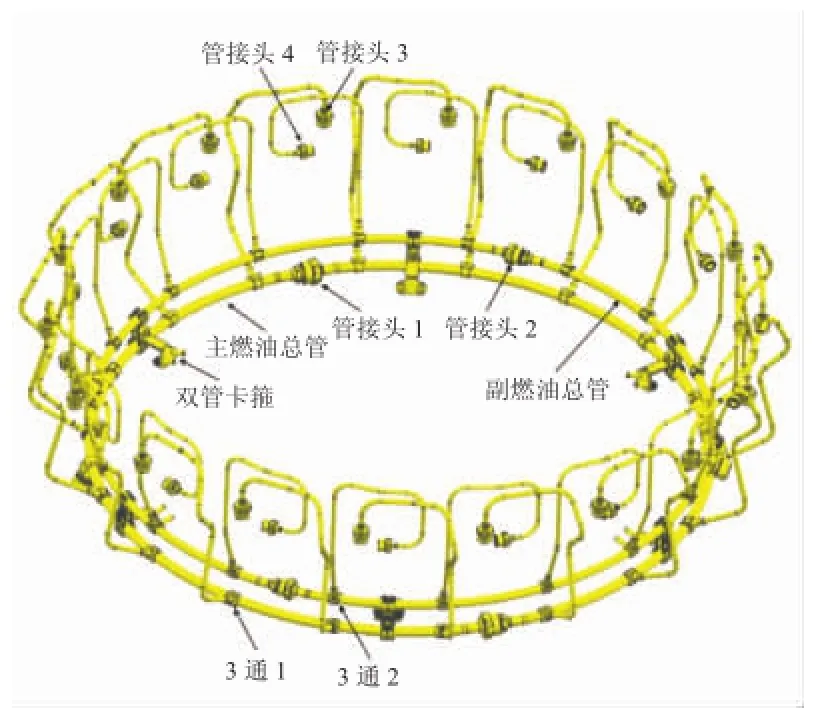
图1　燃油管路系统

燃油管路系统在结构上存在以下鲜明特点：

（1）系统管路分主、副2路，管路数量众多，且为结构复杂的3维管路；

（2）管路系统部件之间相互连接，连接结构有3通、主管接头、分管接头等多种连接方式，连接形式多样；

（3）支撑结构为带有支架的双管卡箍，卡箍内圈有柔性衬套（为弹性支撑），在分析系统的振动特性时需要计算卡箍的支撑刚度；

（4）燃油分管呈周期对称分布，但因为管接头等其他部件，管路系统在整体上并不是严格意义的周期对称结构；

（5）管内充满燃油，振动具有流固耦合特点，系统的动力学特性复杂。

从上述特点可以看出，燃烧室管路系统属于复杂的3维管路系统。

2　燃油管路系统的有限元模型

建立燃油管路系统的有限元模型需要综合考虑单元类型和数量、计算精度和复杂程度等。根据燃油管路系统的结构特点，分析各部件的有限元模拟方法，建立系统的有限元模型。

2.1管路有限元模型

燃油总管和分管是燃油管路系统的主要组成部分，应用有限元法建立模型需要对结构进行离散，可供选择的单元主要有实体单元、壳单元、管单元。其中实体单元和壳单元建模更接近原几何模型，能够考虑流固耦合振动问题，但建模及分网复杂，适于分析简单管路振动问题。管单元基于梁单元，截面参数设置方便，建模简单，适合分析结构复杂的管路系统。

燃油管路系统的分管数量多、结构复杂，因此采用管单元进行建模。文献［9］采用管单元有限元法计算了L型管路的固有频率，并与试验结果对比，验证了管单元分析管路振动问题的准确性。1段分管的几何模型及有限元模型如图2、3所示。

图2　管路几何模型

图3　管路单元模型

2.2管内燃油的有限元模型

燃油管路作为充液管路的1种，其振动问题是典型的充液管路流固耦合振动问题。根据文献［10-11］可知，充液管路各阶频率随流速加快而降低，当达到临界速度时，固有频率降为零，系统失稳；但在远离临界速度区域，频率变化十分平缓；压力对管路频率影响较小，一般可以忽略不计。燃油管路燃油流速相对较慢［12］，可忽略流速及压力影响，只考虑流体质量影响，故采用附加质量法模拟管内流体。

附加质量法是指将流体对结构的作用以附加质量的形式表达。燃油管路系统的运动微分方程为

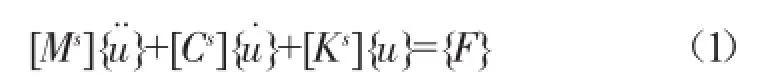
式中：［Ms］、［Cs］、［Ks］分别为燃油管路系统的质量、阻尼、刚度矩阵；｛u｝、｛u.｝、｛u¨分别为燃油管路的位移、速度、加速度向量；｛F｝为燃油管路系统的外载荷。

用附加质量法对流体处于静止或小幅值运动的充液管路系统进行计算时，只考虑流体质量对管路系统动力特性的影响，把流体质量转化到管路系统质量上，忽略实际管路中存在的流固相互作用的影响。考虑流体对结构的附加质量建立的系统振动有限元方程为

式中：［Ms］、［Mf］分别为管道结构质量和管内流体质量矩阵；［Ks］为系统刚度矩阵，可以考虑流体压力对系统刚度的影响；｛F｝为结构所受外载荷。

2.3管路连接件有限元模型

管路系统连接件（如图4所示）用于连接不同的管路，并起到密封作用。管路系统连接件的刚度较大，因此不考虑其弹性影响，但质量较大且集中，其质量特性对管路系统的动力学特性影响显著，因此采用MASS21质量单元对管路连接件进行有限元建模。单元的节点坐标选取连接件的质心坐标，质量特性通过定义实常数进行添加，并将连接件节点与相邻导管的节点通过自由度耦合进行连接，使连接件的节点成为管路连续系统的一部分。

图4　管路连接件模型

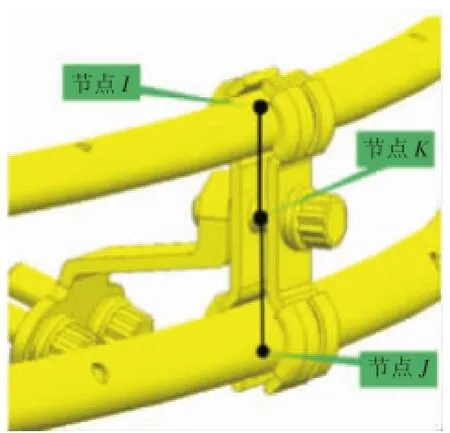
图5　双管卡箍几何模型

2.4双管卡箍有限元模型

燃烧室管路系统的支撑结构是带有支架的双管卡箍，主要用来连接燃油主管并将其固定到机匣上。双管卡箍的几何模型如图5所示。卡箍内圈是1层聚四氟乙烯衬垫，起到阻尼减振的作用，卡箍对管路系统的支撑刚度相对总管较小，属于弹性支撑。在振动分析中，将双管卡箍及支架部分作为1个整体考虑，其力学模型等效为6个自由度方向的支撑刚度。

双管卡箍的等效刚度采用Ansys软件中的Matrix27单元进行模拟，该单元具有2个节点，可以通过定义单元刚度矩阵来描述单元在6个自由度方向上的刚度。由图5可知，在双管卡箍支撑的管路中心点和卡箍中间位置分别建立I、J、K 3个节点，3个节点之间建立2个Matrix27单元，并分别定义单元刚度矩阵；在中间节点K施加固定约束模拟卡箍支架固定到机匣上，I、J 2个节点通过与管路节点的共享，模拟管路与卡箍的连接处，双管卡箍的有限元模型如图6所示。

图6　有限元模型

3　管路支撑刚度

刚度表示物体抵抗变形的能力，定义为力与位移之比，即

式中：δi为i方向施加集中力Fi所产生的线位移；δij为角方向ij施加力矩Mij所产生的角位移。

管路系统的支撑刚度是影响其固有频率及振型的重要因素之一。根据文献［8］，支撑刚度增大，管路系统固有频率增大直至稳定；支撑刚度影响振动传递效率，刚度越大，振动传递效率越高。因此准确求解管路系统的支撑刚度对于管路系统的动力学分析非常重要。

燃油管路系统的支撑结构为带支架的双管卡箍（图5）。文献［12］采用有限元法计算了卡箍刚度，并通过试验验证了有限元计算的正确性，本文采用类似方法，建立带支架的双管卡箍有限元模型，并求解其支撑刚度。

卡箍简化成弹性支撑，共具有6个自由度方向的刚度，分别是X、Y、Z方向的平动刚度和绕这3个方向的转动刚度，即Kx、Ky、Kz、Kxy、Kxz、Kyz。

管路系统双管卡箍的有限元模型（图6）用2段实体刚性杆代替主、副燃油总管，以方便施加载荷且通过设置较大的弹性模量最大限度地降低因管路变形引起的计算误差。卡箍及支架材料为0Cr18Ni9，衬垫材料为聚四氟乙烯，材料参数见表1，在有限元模型中对不同材料分别进行定义。

燃油管路的振动以横向弯曲振动为主，认为管路不存在沿管路轴线方向的滑动和绕轴线的相对转动，所以认为Ky、Kxz为无穷大，6个方向的刚度简化成4个，分别是Kx、Kz、Kxy、Kyz。

双管卡箍对燃油主、副总管都有支撑作用，在求解等效刚度时需要分别计算。主、副总管的直径分别为12、10 mm，如图7所示。D12和D10代表主管路系统和副管路系统。从图中可见，以D12卡箍X方向平动刚度为例，在D12刚性杆端面中心点施加X方向载荷Fx，在D10刚性杆端面中心点以及卡箍支架螺栓固定处施加固定约束，进行静力分析，获得D12中心点X方向位移，根据式（3）计算得到X方向刚度Kx。同理，可以计算得到其他方向以及D10卡箍的等效刚度，计算结果见表2。根据计算结果即可建立管路系统的支撑刚度矩阵。

表1　材料性能参数

图7　双管卡箍实体有限元模型

表2　双管卡箍等效支撑刚度

4　燃油管路系统模态分析

4.1边界条件和载荷

根据上述对管路部件建模分析的结果，建立燃油管路系统的有限元模型，如图8所示。采用有限元法，网格划分越精细，计算结果越精确，但计算效率随之降低。本文模型主要为管单元，在分管弯管处适当地加密网格来体现弯管特性，划分网格后有限元模型的节点数为2294，单元数量为1196，单元数量继续增加时，计算结果基本不变，说明网格已足够精细。

图8　燃烧室管路系统有限元模型

边界条件方面，主、副燃油分管连接双油路喷嘴，喷嘴与机匣连接，喷嘴和机匣刚度比燃油管路的刚度大，因此将喷嘴支撑简化为刚性支撑，在分管与喷嘴连接处施加固支约束。卡箍支撑为弹性支撑，认为机匣刚度远大于卡箍支撑刚度，在卡箍与机匣固定位置施加固定约束。

通常采用燃油对滑油系统进行冷却，因此发动机工作时燃油温度高于常温，根据燃油雾化要求，喷嘴前燃油温度一般不超过150℃［13］。本文假定管路温度与燃油温度相同，设置为100℃，参考温度为20℃。

管路材料为某型高温合金，由《航空材料手册》［14］可知，材料参数在200℃以内随温度变化不大，因此设为定值。弹性模量为205 GPa，密度为8440 kg/m3，泊松比为0.308，膨胀系数为12.3×10-6；管内燃油密度为802.4 kg/m3。

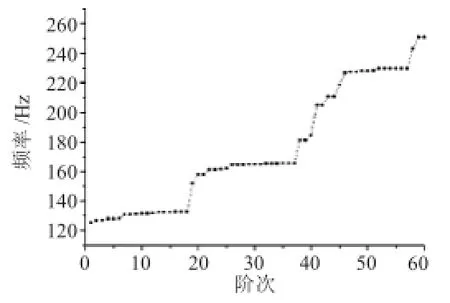
图9　燃油管路系统固有频率曲线

4.2固有频率分析

施加边界条件和温度载荷对燃油管路系统进行静力分析，计算得到热应力分布，再进行有预应力的模态分析，采用Block Lanczos法求解管路系统的固有特性。该算法是经典Lanczos算法的改进算法，将经典Lanczos算法的递归向量改为向量块同时与斯特姆序列检查相结合，提高了算法的稳定性以及收敛性。得到前60阶固有频率阶次曲线，如图9所示。

从图中可见，系统第1阶频率为125 Hz，系统固有频率曲线整体呈“阶”状、分簇的特点，说明燃油管路系统频率及振型为典型的密集分布型。这是由于系统中有许多结构相同的分管，系统整体上呈现一定的周期对称特点，1种振动形式会重复出现在不同区域，所以存在图中频率密集的区域。同时，由于存在系统中管接头等其他部件，导致结构并不是严格意义的周期对称，因此系统并没出现重复频率，同一振动形式的模态频率会有些许波动。

4.3振动模态分析

系统分为主、副燃油管，外圈管路为主燃油管，内圈管路为副燃油管。管路系统的模态振型主要分为主、副燃油分管主导振型以及分管与总管耦合振动模态。

相对总管刚度，燃油分管刚度较小，故低阶频率主要对应分管主导振型；分管数量较多，呈对称周期排列，因此同一振动形式的分管主导振动模态都成簇出现，对应频率曲线中的某一“阶”区域。燃油主、副分管主导的振动模态如图10～12所示。其中图10为以副燃油分管径向振动为主的振动模态，对应频率曲线的第1阶，频率范围是125～133 Hz；图11为以主燃油分管径向振动为主振动模态，对应频率曲线的第2阶，频率范围是158～165 Hz；图12以副燃油分管周向振动为主的振动模态，对应频率范围是210～230 Hz。

图10　副燃油分管径向振动模态

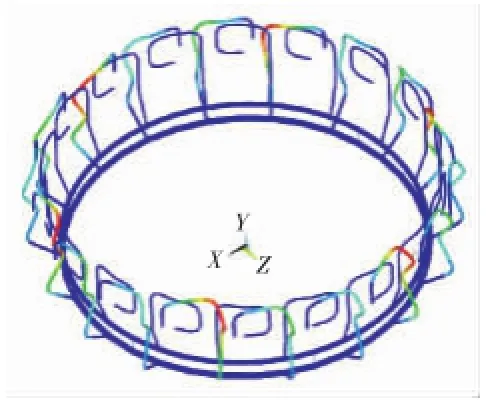
图11　主燃油分管径向振动模态

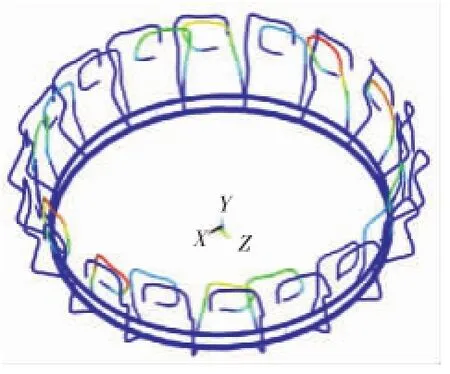
图12　副燃油分管周向振动模态

总管-分管耦合振动模态如图13、14所示，这类振动模态对应频率曲线阶跃部分，其中图13为副燃油管耦合振动模态，振动频率为165 Hz，图14为主燃油管耦合振动模态，振动频率为184 Hz。从图中可见，耦合振动的振动形式比较复杂，振动范围较广，危害更大，因此需要格外关注其共振频率，采取措施防止这类共振发生。

图13　副燃油总管-分管耦合振动振型

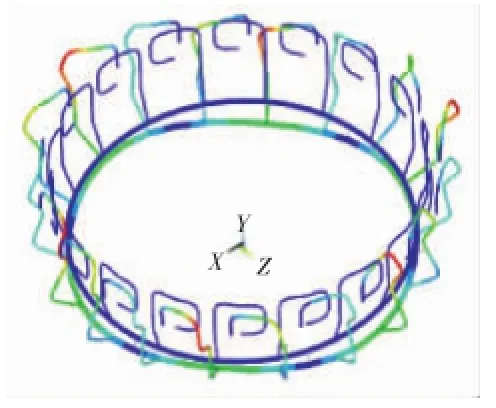
图14　主燃油总管-分管耦合振动振型

4.3系统共振评估

在发动机工作时，管路会遇到各种类型的周期性激励，当这些激励的频率与管路的某1阶固有频率相等时，会引起管路的共振［15］。燃油管路激励有多种，一般考虑高、低压转子不平衡导致的周期性激励，忽略流体脉动、气动激励等随机激励［16］。对于共振裕度，将发动机额定转速上下浮动10%作为共振激励频率范围。具有上述燃油管路系统的发动机额定转速一般为8000 r/min，即激振频率为133 Hz，其共振频率范围为120～147 Hz。

从图9中可见，管路系统第1阶振动频率为125～133 Hz，第2阶振动频率范围为158～184 Hz，其中第1阶频率落入共振频率范围内，极有可能发生危险共振。由前述可知，第1阶频率范围的振动以副燃油分管的径向振动为主，因此燃油分管更有可能发生振动破坏，需要优化燃油分管振动特性，采取以下措施：

（1）通过更换导管类型改变管路振动特性，例如将钢管改为软管［17］，大幅降低分管的振动幅度，将振动应力减小到可接受范围内；

（2）优化分管的空间结构，通过改变分管空间走向和管长等达到改变振动频率、减小振动应力的目的；

（3）通过改变支撑结构的形式、位置或支撑数量来提高系统支撑刚度，使得系统第1阶固有频率高出共振频率范围。

在实际工程应用中，需要结合发动机管路的实际工作环境，综合考虑燃油流量、管路质量、空间大小等其他因素，合理选择上述1条或几条措施来优化燃油管路系统的振动特性。

5　结论

本文系统研究了航空发动机双路总管燃油管路系统的有限元模拟技术，求解了双管卡箍的支撑刚度，建立起系统的有限元模型，并对其固有振动特性进行了分析，得到以下结论：

（1）航空发动机双路总管燃油管路系统的有限元模拟技术主要体现在管单元模拟管路、附加质量法模拟管内流体、质量元模拟管接头、矩阵单元模拟卡箍支撑及支撑刚度的求解；建立了系统的振动有限元模型，可用于管路系统有限元分析。

（2）采用有限元法的静力分析求解了双管卡箍的支撑刚度，提高了燃油管路系统支撑刚度矩阵的合理性以及系统振动分析的准确性。

（3）该燃烧室管路系统以分管振动为主，振动模态具有分簇特点，可分为主、副燃油分管主导模态以及分管-主管耦合模态。

（4）对燃油管路系统进行共振评估，副燃油分管最有可能发生共振，需要针对分管采取合理措施优化振动特性。

［1］吉世强.航空发动机检验技术手册［M］.北京：航空工业出版社，2008：245-246. Ji Shiqiang.Aero-engine inspection technical manuals［M］.Beijing：Aviation Industry Press，2008：245-246.（in Chinese）

［2］杨绍孔.飞机液路与气路系统的安装和试验［M］.北京：国防工业出版社，1980：75-77. YANG Shaokong.Aircraft hydraulic and pneumatic system installation and testing［J］.Beijing：National Defense Industry Press，1980：75-77.（in Chinese）

［3］Barry L S.The importance of engine external health［C］//The 7th International Symposium on Transpoa Phenomena and Dynamws of Rotating Machinery（volume A）.Hawaii，1998：572-580.

［4］Sreejith B，Jayaraj K，Ganesan N，et al.Finite element analysis of fluid structure interaction in pipeline systems［J］.Nuclear Engineering and Design，2004，227（3）：313-322.

［5］杨莹，陈志英.航空发动机管路流固耦合固有频率计算与分析［J］.燃气涡轮试验与研究，2010，23（1）：42-46. YANG Ying，CHEN Zhiying．Calculation and analysis on natural frequency of fluid structure interaction in aeroengine pipelines［J］.Gas Turbine Experiment and Research，2010，23（1）：42-46.（in Chinese）

［6］刘伟，曹刚，翟红波，等.发动机管路卡箍位置振动灵敏度分析与优化设计［J］.航空振动学报，2012，27（12）：2756-2762. LIU Wei，CAO Gang，ZHAI Hongbo，et al．Sensiticity analysis and optimization design of supports’positions for engine pipelines［J］.Journal of Aerospace Power，2012，27（12）：2756-2762．（in Chinese）

［7］贾志刚，陈志英.基于参数化的航空发动机管路调频方法研究［J］.航空发动机，2008，34（4）：34-37. JIA Zhigang，CHEN Zhiying.Investigation of frequency modulation for aeroengine pipeline based on parameterization［J］.Aeroengine，2008，34（4）：34-37.（in Chinese）

［8］黄益民，葛森，吴炜，等.不同支撑刚度对输流管道系统动力学特性完整性影响［J］.振动与冲击，2013，32（7）：165-169. HUANG Yimin，GE Sen，WU Wei，et al.Effect of different supporting rigidities on dynamic characteristics integrity of a pipeline conveying fluid［J］.Journal of Vibration and Shock，2013，32（7）：165-169.（in Chinese）

［9］侯文松，陈志英，邱明星，等．充液弯管固有频率试验与计算分析［J］.航空发动机，2013，39（2）：84-89． HOU Wensong，CHEN Zhiying，QIU Mingxing，et al.Experiment and calculation analysis of natural frequency of charging line［J］.Aeroengine，2013，39（2）：84-89.（in Chinese）

［10］许萍，李著信，蒋忠.液体输送管道固液耦合振动的有限元分析［J］.管道技术与设备，2004（6）：3-5. XU Ping，LI Zhuxin，JIANG Zhong.FEM analysis for fluidstructure coupling vibration of fluid conveying pipe［J］.Pipeline Technique and Equipment，2004（6）：3-5.（in Chinese）

［11］王世忠，王茹.三维管道固液耦合振动分析［J］.哈尔滨工业大学学报，1992，24（4）：43-49. WANG Shizhong，WANG Ru.Solid liquid coupling vibration analysis of three-dimensional pipeline［J］.Journal of Harbin Institute of Technology，1992，24（4）：43-49.（in Chinese）

［12］尹泽勇陈亚农.卡箍刚度的有限元计算与试验测定［J］.航空动力学报，1999，14（2）：179-182. YIN Zeyong，CHEN Yanong.Finite element calculation and testing of clamp stiffness［J］.Journal of Aerospace Power，1999，14（2）：179-182.（in Chinese）

［13］张东辉.高温燃油对航空发动机控制系统的影响分析［J］.航空发动机，2013，39（1）：12-16. ZHANG Donghui.Influence of high fuel temperature on aeroengine control system［J］.Aeroengine，2013，39（1）：12-16.（in Chinese）

［14］中国航空材料手册编辑委员会．中国航空材料手册（第2卷）［M］.北京：中国标准出版社，2002：324-325．Editorial Board of China Aviation Materials Manual.China aviation materials manual（volume 2）［M］.Beijing：China Standards Press，2002：324-325.（in Chinese）

［15］航空发动机设计手册总编委会.航空发动机设计手册（第19册）［M］.北京：航空工业出版社，2000：196-198．Editorial Board of Aeroengine Design Manual.Aeroengine design manual（volume 19）［M］.Beijing：Aviation Industry Press，2000：196-198.（in Chinese）

［16］李琳.发动机管道振动的优化［C］//第七届发动机结构强度振动学术会议论文集.洛阳：中国航空学会，1994：266-269．LI Lin.Engine pipeline vibration optimize［C］//The 7th Aeroengine Structure Strength and Vibration Academic Conference Proceedings. //Luoyang：China Aviation Society，1994：266-269.（in Chinese）

［17］赵传亮，尚守堂，马宏宇，等.燃气轮机燃烧室中的管路设计［J］.航空发动机，2014，40（5）：39-44. ZHAO Chuanliang，SHANG Shoutang，MA Hongyu，et al.Design of pipelines for gas turbine combustor［J］.Aeroengine，2014，40（5）：39-44.（in Chinese）

（编辑：赵明菁）

Research on Finite Element Simulation Technology of Fuel Pipe System Vibration Characteristics

ZHAO Wei-zhi，CHEN Zhi-ying
（School of Energy and Power Engineering，Beihang University，Beijing 100191，China）

Aircraft engine fuel pipe is a three-dimensional pipeline system，mainly used for fuel supply.In order to analyze the vibration characteristics，taking dual fuel line system as an example，combining clustered lines，diversified connection structures，specific bracing structures and pipe with injecting liquids，the finite element simulation method has been systematically studied.Bracing stiffness of pipeline system，which has great influence on vibration characteristics，was analyzed by the finite element static method.Combining the above analysis methods of different components，the finite element model of vibration system was established.After modal analyzed the pipeline system，natural frequency change rule of the vibration system was obtained.The analysis results show that the mode of vibration has cluster characteristics.After the resonance evaluation of the system，vice fuel line branch was considered most possibly to resonate，and some reasonable optimization suggestions were proposed.

fuel pipe；vibration characteristics；bracing stiffness；finite element method；aeroengine

V 235.1

A

10.13477/j.cnki.aeroengine.2016.01.009

2015-01-22

赵伟志（1989），男，在读硕士研究生，研究方向为航空发动机管路结构振动；E-mail：zhwzhsky@163.com。

引用格式：赵伟志，陈志英.燃油管路系统振动特性有限元技术研究［J］.航空发动机，2016，42（1）：42-47.ZHAO Wei zhi，CHEN Zhiying.Research on finite element simulation technology of fuel pipe system vibration characteristics［J］.Aeroengine，2016，42（1）：42-47.