超指数跳扩散模型下动态保护基金的定价

刘孔洁，董迎辉，朱海飞

（苏州科技学院数理学院，江苏苏州215009）

超指数跳扩散模型下动态保护基金的定价

刘孔洁，董迎辉*，朱海飞

（苏州科技学院数理学院，江苏苏州215009）

在标的基金价格服从超指数跳扩散模型假设下，考虑了动态保护基金的定价问题。利用首中时分布的拉普拉斯变换，给出了动态保护基金价格拉普拉斯变换的显示表达公式。

动态保护基金；超指数跳扩散模型；拉普拉斯变换

由Gerber和Shiu[1]，以及Gerber和Pafumi[2]引入的动态保护基金，最近成为保险行业最受欢迎的投资基金之一。保护是动态的是因为每当基金的价格低于某个阀值时，基金价格会通过发行人注入资金来提升，实际上，一个动态保护基金可以分解为一个全裸的基金和动态保护。因此，个人和机构投资者可以使用这些产品规避投资组合的下行风险。由于该基金为投资者提供了一个比传统的欧式看跌期权更为复杂且更为有利的收益结构，因此，该基金的价值将比传统的看跌期权更大，其定价问题也更为复杂。文献[2]在Black-Schole模型框架和常利率假设基础上，给出了动态保护基金的定价公式。董迎辉[3]在Black-Schole模型和随机利率模型框架下，研究了动态保护基金的定价问题。然而，Black-Schole模型不能描述股票收益率厚尾尖峰的特点，随机波动率模型则改进了Black-Schole模型，具体可参见文献[4]，另一类比较流行的模型是跳扩散模型。Merton[5]首次考虑用跳扩散过程来描述资产的价格过程，虽然跳扩散过程弥补了Black-Schole模型的很多不足之处，但在一般的跳扩散模型下很难给出一些依赖于路径的期权的定价公式，如，在文献[5]所提出的正态跳扩散模型下，虽然能得到欧式期权的定价公式，但却无法给出奇异期权（如美式期权、回望期权等）的定价公式。

Kou和Wang[6－7]提出了用双指数跳扩散模型来描述股票的价格过程，利用指数分布的无记忆性，一些奇异期权（如障碍期权、回望期权、永久美式期权）的闭型定价公式可以得到。受此启发，在文中，笔者将考虑用几何超指数跳扩散模型来描述股票的动态。事实上，超指数跳扩散过程是一类比双指数跳扩散过程更一般的风险模型，它不仅能刻画资产投资回报的厚尾尖峰性，还能用来近似任意的跳扩散过程。在该模型下，笔者将给出动态保护基金价格的拉普拉斯变换，利用数值算法反演所得到的拉普拉斯变换，便能得到动态保护基金价格的数值解。

文中的内容安排如下：第一部分介绍了动态保护基金的概念和标的基金价格的动态；第二部分给出了超指数跳扩散模型下，动态保护基金价格拉普拉斯变换的表达公式；第三部分是结论。

1　超指数跳扩散模型下的动态保护基金

假设标的基金的价格过程服从如下的几何超指数跳扩散过程

其中F（0）＞0为基金的初始价格，r＞0为无风险利率，σ＞0为扩散系数，W（t）是一个标准布朗运动，N（t）是一个强度为λ的泊松过程，{Yi，i＝1，2，…}是一个独立同分布的超指数随机变量序列，其共同的密度函数为

其中0＜K≤F（0）为一常数。由定义（4）可知，动态保护基金的收益将始终高于K。

2　动态保护基金的价格公式

令DGF0（F（0），T）表示具有到期日为T的动态保护基金在0时刻的价格。则由资产定价理论得

因此，具有到期日为T的动态保护基金合同所提供的动态保护在0时刻的价格为

为了给出DGF0（F（0），T），以及DP0（F（0），T）的表达公式，定义一个新测度

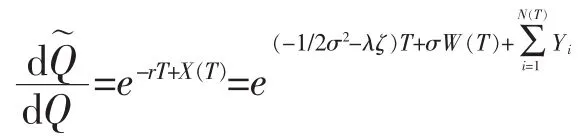
令b=ln（K/F（0））＜0。则由测度变换，（6）变为

由于在跳扩散模型下，很难给出最小值分布的表达公式，因此，文中也无法给出（8）式的闭型公式。幸运的是，人们能够给出超指数跳扩散模型下首中值分布的拉普拉斯变换，受此启发，笔者将考虑DGF0（F（0），T）的拉普拉斯变换。

定义X的首中时为

引理令X为（7）式所描述的超指数跳扩散过程，则对任意的δ＞0，X首中时的拉普拉斯变换为

其中r1，r2，…，rm+1是下列方程

的m+1个不同的负根，系数c1，c2，…，cm+1满足

证明可参见文献[8]。

注如果允许（3）式中的某些pi或qi取负数，则{Yi，i＝1，2，…}是一个独立同分布的混合双指数随机变量序列，此时，方程（9）不一定有m+1个不同的负根，因此，X首中时的拉普拉斯变换也不一定具有该文引理中的表达形式。

利用文中引理便可得出的拉普拉斯变换。

定理对任意的δ＞0，到期日为T的动态保护基金在0时刻的价格DGF0（F（0），T）的拉普拉斯变换为

其中b=ln（K/F（0）），r1，r2，…，rm+1是方程（9）的m+1个负根，c1，c2，…，cm+1满足（10）。

证明经简单运算可得

则DGF0（F（0），T）的拉普拉斯变换为

其中最后一个等式是由文中引理得到的。

推论对任意的δ＞0，到期日为T的动态保护基金所提供的动态保护在0时刻的价格DP0（F（0），T）的拉普拉斯变换为

其中b=ln（K/F（0）），r1，r2，…，rm+1是方程（9）的m+1个负根，c1，c2，…，cm+1满足（10）。

证明DP0（F（0），T）的拉普拉斯变换为

利用文中定理立得结论。

3　结语

笔者提供了一个超指数跳扩散模型下，为动态保护基金定价的方法。动态保护基金可以分解为期权和标的基金的组合，利用首中时分布的拉普拉斯变换，给出了动态保护基金价格拉普拉斯变换的闭型表达公式，从而可以通过拉普拉斯反演算法（如Gaver-Stehfest算法）给出动态保护基金价格的数值解。

[1]GERBER H U，SHIU E S W.From ruin theory to pricing reset guarantees and perpetual put options[J].Insurance：Mathematics and Economics，1999，24（1-2）：3-14.

[2]GERBER H U，PAFUMI G.Pricing dynamic investment fund protection[J].North American Actuarial Journal，2000，4（2）：28-37.

[3]董迎辉.Vasicek利率模型下具有随机障碍的动态保障年金的定价[J].应用概率统计，2013，29（3）：237-245.

[4]GRISELDA D，GREGORY R.Pricing variable annuity guarantees in a local volatility framework[J].Insurance：Mathematics and Economics，2013，53（3）：650-663.

[5]MERTON R C.Option pricing when underlying stock returns are discontinuous[J].Journal of Financial Economics，1976，3：125-144.

[6]KOU S G，WANG H.Option pricing under a double exponential jump diffusion model[J].Management Science，2004，50：1178-1192.

[7]KOU S G，WANG H.First passage times of a jump diffusion process[J].Advance of Applied Probability，2003，35：504-531.

[8]DONG Y H，WANG G J，WU R.Pricing zero-coupon bond and its fair premium under a structural credit risk model with jumps[J].Journal of Applied Probability，2011，48：404-419.

Pricing dynamic guaranteed funds under the hyper-exponential jump-diffusion model

LIU Kongjie，DONG Yinghui，ZHU Haifei
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

We evaluate the price of dynamic guaranteed funds under the assumption that the price of underlying naked fund follows the hyper－exponential jump-diffusion process.Based on the Laplace transform of the first passage time,we derive the closed-form expression for the Laplace transform of the price of dynamic guaranteed funds.

dynamic guaranteed funds；hyper－exponential jump－diffusion model；Laplace transform

O211．5MR（2000）Subject Classification：93E15

A

1672－0687（2016）01－0041－04

责任编辑：谢金春

2013－10－31

国家自然科学基金资助项目（11301369）；江苏省自然科学基金资助项目（BK20130260）；本科生实践创新训练计划项目（201310332062X）

刘孔洁（1993-），男，江西赣州人。*

董迎辉（1978-），女，副教授，博士，硕士生导师，E－mail：dongyinghui1030@163.com。