关于方程f（k）+Ak-1f（k-1）+…＋Asf（s）+…+A1f′＋A0f＝0解的增长性

胡梦薇，孙桂荣

（苏州科技学院数理学院，江苏苏州215009）

关于方程f（k）+Ak-1f（k-1）+…＋Asf（s）+…+A1f′＋A0f＝0解的增长性

胡梦薇，孙桂荣*

（苏州科技学院数理学院，江苏苏州215009）

研究高阶微分方程f（k）+Ak-1f（k-1）+…＋Asf（s）+…+A1f′＋A0f＝0解的增长性，运用Nevanlinna理论和复域微分方程理论，在一定条件下得到上述方程的每一个非零解都是无穷级，推广并完善了文献[1]的结果。

增长级；线性微分方程；整函数

1　引言及其主要结果

文中将考虑高阶的线性微分方程

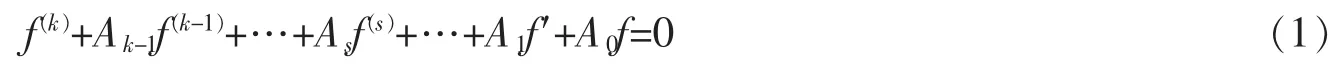
其中，Aj（j=0，1，…，k-1）是整函数。文中将使用亚纯函数理论的标准记号[2-3]。特别地，对于一个亚纯函数f（z），用ρ（f）表示f（z）的增长级，用λ（f），λ（1/f）分别表示f（z）的零点和极点的收敛指数。

目前，许多学者针对下面的二阶方程

已经作了许多研究。并且知道当方程（2）的系数是整函数时，方程所有的解都是整函数。特别地，如果A，B至少有一个为超越时，并且当f1，f2是方程（2）的两个线性无关解时，这两个线性无关解中至少有一个解的增长级是无穷。然而，也存在一些形如（2）式的方程，它们具有有限级的非零解。例如f（z）=e-z-1满足方程f″+ ezf′-f=0。然后，有学者继续考虑当系数A（z），B（z）满足何种条件时可以保证方程（2）的每一个非零解都是无穷级的情况，得出：若A（z），B（z）都是整函数且ρ（A）＜ρ（B）；或者A（z）是多项式，B（z）是超越整函数；或者ρ（B）＜ρ（A）＜1/2，则方程（2）的所有非零解都是无穷级[4-5]。

自然地，如果考虑当ρ（A）=ρ（B）或者ρ（A）＞1/2且ρ（B）＜ρ（A）时，方程（2）的所有非零解是否具有无穷级呢？一般地，这个猜想是不成立的，可以在文献[6]中找到许多的反例。注意到，当P（z）是n次多项式，关于形如f″+P（z）f=0的微分方程，前人已经作了很多研究，并且总结出此方程的解的许多重要的性质[7-8]。在文献[1]中，作者通过考察方程系数的性质，得到了如下的结果。

定理1设A（z）是方程f″+P（z）f=0的非零解，其中P（z）=anzn+…+a0（an≠0），B（z）是超越整函数且ρ（B）≤1/2，则方程f″+Af′+Bf=0的每一个非零解都是无穷级。

那么，如果继续考虑把这里的二阶方程f″+Af′+Bf=0推广到高阶方程（1）的情形，会不会同样也有方程（1）的每一个非零解都是无穷级呢？

众所周知，当方程（1）的系数Aj（j=0，1，…，k-1）都是多项式时，方程的解都是有限级的；当方程（1）的系数都是整函数并且ρ（Aj）＜ρ（A0）≤1/2时，方程（1）的每一个非零解都是无穷级。文中考虑，如果有其中一个系数As（s≠0）的级ρ（As）＞1/2且ρ（Aj）＜ρ（A0）≤1/2（j≠0，s）时的情况，经过证明得到下面的结果。

定理2把f″+P（z）f=0的一个非零解当做微分方程（1）的系数，记为As（z）（s≠0），而Aj（j≠0，s）是有限级超越整函数，并且有ρ（Aj）＜ρ（A0）≤1/2。则微分方程（1）的每一个非零解都是无穷级。

2　引理

首先需要给出一些记号，假设α＜β且β-α＜2π，则对于任意r＞0，文中分别定义S（α，β）={z：α＜argz＜β}和S（α，β，r）={z：α＜argz＜β}∩{z：|z|≤r}。假设f（z）是一个有穷正级整函数，S={z：α≤argz≤β}是一个角域，对任意θ（α＜θ＜β），有

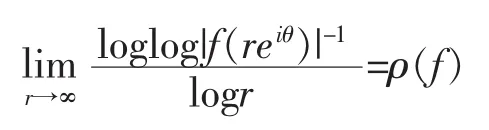
则称f（z）在角域S中以指数形式趋于零。类似地，如果对任意θ（α＜θ＜β），有

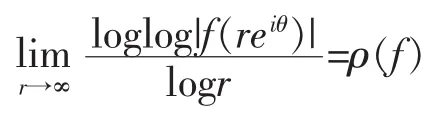
则称f（z）在角域S中以指数形式趋于无穷。

为给出下面的引理，对于E⊂[0，∞），记E的Lebesgue测度为m（E）；对于E⊂[1，∞），定义E的对数测度为，并且E的上对数密度和下对数密度分别定义为

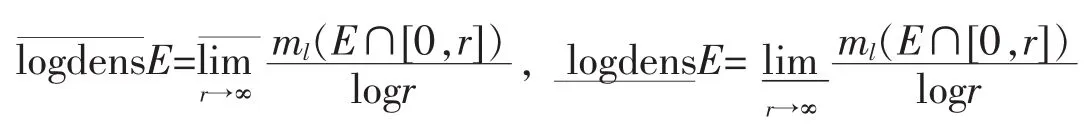
下面的引理1在文中定理的证明中有着重要作用。

引理1[8]假设f（z）是方程f″+P（z）f=0的一个非零解，其中P（z）=anzn+…+a0（an≠0），且设

其中，j=0，1，2，…，n+1，则f（z）具有下列性质：

（1）在每一个角域Sj中，f要么以指数形式趋于无穷，要么以指数形式趋于零。

（2）若f在角域Sj中以指数形式趋于零，则f在角域Sj-1和角域Sj+1（若j=n+1则Sj+1=S0）中都以指数形式趋于无穷。然而，f（z）可以在任意两个相邻角域内以指数形式趋于无穷。

（3）若在角域Sj中f指数形式趋于零，那么在角域的任意闭子集中，f至多具有有穷多个零点。

（4）若在相邻角域Sj-1和Sj中，f都以指数形式趋于无穷，那么对任意ε＞0，在角域θj-ε≤argz≤θj+ε中f（z）具有无穷多个零点，且当r→∞时，有

其中n（Ω（θ-ε，θ+ε，r），f＝0）表示f（z）在角域Ω（θ-ε，θ+ε，r）＝{z：θ-ε≤argz≤θ+ε，0＜|z|≤r}中的零点个数，重级零点按其重数计算。

引理2[9]假设（f，Γ）是满足如下要求的有序数对：f（z）是一个有穷级超越亚纯函数，Γ={（k1，j1），（k2，j2），…（kq，jq）}是一个互不相同的二元整数组构成的有限集，使得ki，＞ji≥0，i=1，2，…，q，则对任意给定的常数ε＞0，下列三个论断成立：

（1）存在集合E1⊂[0，2π），其测度m（E1）＝0，使得当ψ0∈[0，2π）-E1，存在常数R0=R0（ψ0）＞0，使得对所有满足argz＝ψ0，|z|≥R0的z及所有的（k，j）∈Γ，下列不等式

成立。

（2）存在具有有限对数测度的集合E2⊂（1，∞），使得对于满足|z|（E2∪[0，1]）的所有z及所有的（k，j）∈Γ，不等式（3）成立。

（3）存在具有有限线性测度的集合E3⊂[0，∞），使得对于满足|z|E3的z及所有的（k，j）∈Γ，下列不等式

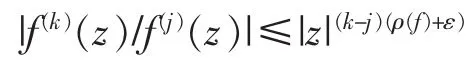
成立。

引理3[10]假设A0（z）堍0，A1（z），…，Ak-1（z）是整函数，对任意实常数k，δ，ε，β，θ1，θ2，其中kδ＜1，k（≥2）是正整数，δ是任意正实数，α＞0，β＞0且θ1＜θ2，当|z|＝r≥rδ时，在角域中S（0）={z：θ1≤argz≤θ2}，对某个s（s=1，2，…，k-1），以及所有的j（j=0，1，…，k-1）且j≠s，有

对任意给定的常数ε＞0，记角域S（ε）={z：θ1+ε≤argz≤θ2-ε}。若f堍0是方程（1）的超越解，且ρ（f）＜∞，则下列结论成立：

（1）当z→∞时，在角域S（ε）中，存在不为零的常数bj（j→∈{0，…，s-1}），使得f（j）→bj。更进一步，有

（2）当z→∞时，在角域S（3ε）中，对每一个正整数m≥j+1，有

文中定理的证明依赖于下面的引理。

引理4[11]假如f（z）是一个整函数，满足ρ（f）≤1/2，则如下两个论断必有一个成立：

（1）对每一个η＜ρ（f），存在序列rn，rn=rn（η），使得对所有满足|z|＝rn的z，有

（2）对每一个η＜ρ（f），定义集合

3　定理2　的证明

假设As（z）是方程

的一个非零解，其中P（z）=anzn+…+a0（an≠0）。由引理1知，As（z）至多有n+2条零点聚值线。

下面将定理的证明分成两种情形进行讨论，为了导出矛盾，现假设f是方程（1）的有限级非零解。

情形1假设As（z）恰有n+2条零点聚值线。根据引理1容易得到在这n+2个角域Sj（j=0，…，n+1）中，As（z）都以指数形式趋于无穷。则对于任意的正数ε，，以及j=0，1，…，n+1，在角域Sj（ε）中，当z→∞时，可以得到

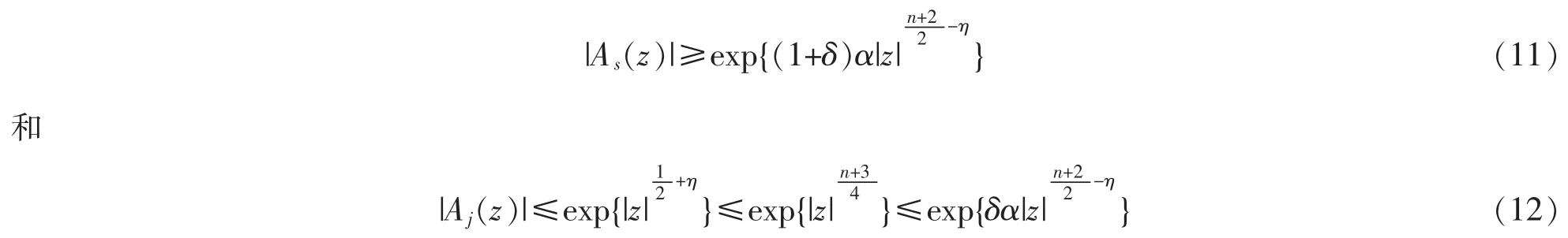
其中α，η是不依赖ε的正的常数。对0≤j≤n+1，由（11），（12）式和引理3知存在相应的bj≠0，使得在角域Sj（ε）中，当z→∞时，有下式成立

特别地，j=0时，有

从而f（z）在Sj（ε）中有界。因此，由Phragmen-Lindel觟f定理知，f（z）在整个复平面上有界。再由Liouville’s定理可得f（z）是非零的常数函数，但是这与f（z）是方程（1）的解矛盾，所以ρ（f）＝∞。

情形2假设As（z）的零点聚值线条数少于n+2。那么，根据引理1可知，至少存在一个角域Sj0（0≤j0≤n+1），使得As（z）在Sj0里以指数形式趋于零。即

这里z＝reiθ∈Sj0。

另外，因为ρ（Aj）＜ρ（A0）≤1/2，所以取max{ρ（Aj）}＜γ1＜γ＜ρ（A0）≤1/2，使得

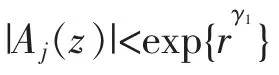
所以，在角域Sj0内，有

再由方程（1）可得

因为A0是整函数，根据引理4，下面分两种情况进行讨论以寻找矛盾。

第一种情况。假设引理4的推断（1）成立，即对于γ＜ρ（A0），存在序列{rn}，rn=rn（γ），当rn→∞时，使得对满足z的，有下式成立

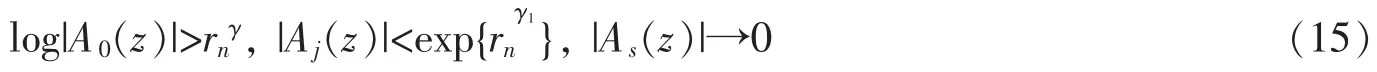
然后，由引理2知由于角域Sj0的张开角度为，所以必然可在Sj0中找到θ0E1，是对于点列zn=rneiθ0有（3）式成立，故，结合（14）和（15）式，有

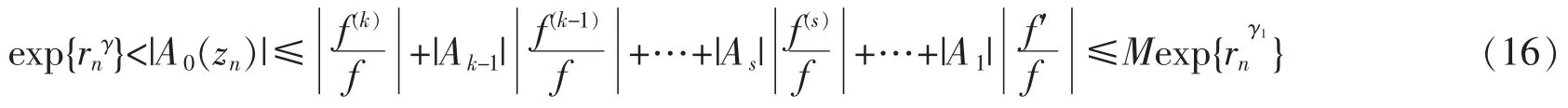
这里的M是正的常数。

因为γ＜γ1，上式显然是矛盾的。

第二种情况。对于γ＜ρ（A0），令

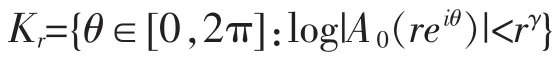
则存在E2＝E2（γ）⊂[0，∞），，使当r→∞，r∈E，有m（Kr）→0。由引理2知，存在集合E3⊂[1，∞），其对数测度ml（E3）＜∞，使得当z满足|z|＝rE3∪[0，1]时，有

记E4＝E2（E3∪[0，1]），则E4是无穷对数测度集。取zn=rneiθ∈Sj0且rn∈E4，θnKr，由（14），（17）式和|As（zn）|→0以及log|A0（zn）|≥rnγ，当n→∞，r→∞时，同样会有（16）式的矛盾情况出现。

综合上述两种情况，所以有ρ（f）＝∞。

[1]吴秀碧，伍鹏程.关于方程f″+Af′+Bf=0解的增长性，其中系数A是一个二阶线性微分方程的解[J].数学物理学报，2013，33A（1）：46-52.

[2]HAYMAN W K.Meromorphic Functions[M}.Oxford：Clarendon Press，1964.

[3]YANG Lo.Value Distribution Theory[M].Berlin：Spring-Verlag；Beijing：Science Press，1993.

[4]BANK S B，LAINE I，LANGLEY J.On the frequency of zeros of solutions of second order linear differential equations[J].Results Math，1986，10：8-24.

[5]FUCHS W H J.Topics in Nevanlinna Theory[M].Washington，DC：Naval Research Laboratory，1970：1-32.

[6]GUNDEONDONRSEN G G.Finite order solution of second order linear differential equations[J].Trans Amer Math Soc，1988，305：415-429.

[7]STRODT W.Contributions to the asymptotic theory of ordinary differential equations in the complex domain[J].Mem Amer Math Soc，1954，13：22-34.

[8]HILLE E.Lectures on Ordinary Differential Equations[M].California，London，Don Mills，Ontario：Addison-Wesley Publiching Company，Reading，Massachusetts-Menlo Park，1969.

[9]GUNDERSEN G G.Estimates for the logarithmic derivative of a meromorphic function，plus similar estimates[J].J London Math Soc，1988，37：88-104.

[10]LAINE I，YANG R H.Finite order solutions of complex linear differential equations[J].Electronic Journal of Differential Equations，2004，65：1-8.

[11]HELLERSTEIN S，MILES J，ROSSI J.On the growth of solutions of f″+gf′+hf=0[J].Trans Amer Math Soc，1991，324（2）：693-706.

On the growth of the solutions of f（k）+Ak-1f（k-1）+…＋Asf（s）+…+A1f′＋A0f＝0

HU Mengwei，SUN Guirong
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

This paper studies the growth of the solutions of f（k）+Ak-1f（k-1）+…＋Asf（s）+…+A1f′＋A0f＝0 by using the Nevanlinna theory and the complex oscillation theory of differential equations.We obtained the precise estimation of the growth of the solutions of this equation,which generalized and improved the results of Reference[1].

order of the growth；linear differential equations；entire function

O174.5MR（2000）Subject Classification：30D35；34M10

A

1672－0687（2016）01－0031－05

责任编辑：谢金春

2013－10－22

国家自然科学基金资助项目（11001057）；江苏省自然科学基金资助项目（BK2010234）

胡梦薇（1987-），女，河南商丘人，硕士研究生，研究方向：复域微分方程，差分方程。*

孙桂荣（1975-），女，讲师，硕士，E－mail：sguirong@139.com。