集值模糊测度的正则性

耿晓妮，吴健荣

（苏州科技学院数理学院，江苏苏州215009）

集值模糊测度的正则性

耿晓妮，吴健荣*

（苏州科技学院数理学院，江苏苏州215009）

在集值模糊测度空间上，给出了集值模糊测度正则性的定义，讨论了有关正则性的部分性质，并证明了上自连续的集值模糊测度必为正则的这一重要结论。

集值模糊测度；上自连续；正则性

文中涉及的集值模糊测度概念实际上是集值测度与模糊测度的结合。集值测度作为集值分析的重要组成部分，于1964年由Vind[1]在一篇关于经济学的文章中首先引进，随后开始快速发展并在经济学、控制理论、最优化理论等众多领域都有广泛的应用。而模糊测度则是于1974年由Sugeno[2]提出的一类非可加测度。借助集函数的上（下）自连续、自连续等重要概念，1984年王震源[3]将经典测度论中的一些重要结论推广到了模糊测度论中，极大地推动了模糊测度的研究。

伴随着集值测度与模糊测度的蓬勃发展，集值模糊测度的概念被提出并受到众多学者的广泛关注[4-9]。如，2009年，Alina Gavrilut[4]利用集合的闵可夫斯基加法，在Banach空间X的非空闭子集类上，利用Hausdorff度量定义了一种集值模糊测度，并初步讨论了它的正则性与非原子性。2011年，吴健荣，柳海燕[5]延续了Alina Gavrilut在Hausdorff意义下建立的集值模糊测度空间的研究，并讨论了集值模糊测度的自连续性。

在文中笔者将延续Alina Gavrilut关于集值模糊测度空间正则性的研究，在集值模糊测度空间中，证明上自连续的集值模糊测度π具有正则性。

在文中，X总表示一个实Banach空间，Pbf（X）表示X上所有非空有界闭子集构成的集类。

设x∈X，A，B∈Pbf（X），称为x到A的距离。记

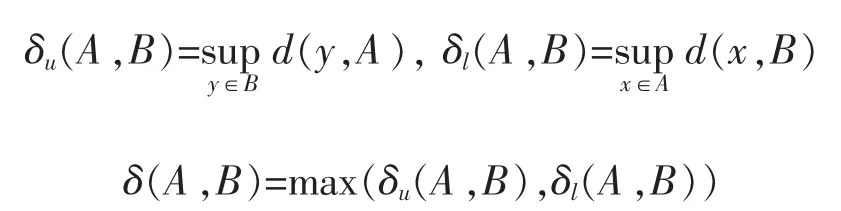
称为A，B间的Hausdorff距离。

设{An}⊆Pbf（X），A∈Pbf（X），若∀ε＞0，∃N，当n＞N时，均有δ（An，A）＜ε，则称集合列{An}依Hausdorff距离收敛到集合A，记为。

1　预备知识

定义1[4]设（Ω，∑）为任意可测空间，集值映射π：∑→Pbf（X）满足以下四个条件：

（2）单调性：若∀A，B∈∑，且A⊆B，则有π（A）⊆π（B）；

2　正则性

定义3（1）对A∈∑，称A关于π是内正则的，若∀ε＞0，都有X中的闭集F∈，使得F⊆A且δ（π（A-F），{}）＜ε。

（2）对A∈∑，称A关于π是外正则的，若∀ε＞0，都有X中的开集G∈，使得A⊆G且δ（π（G-A），{}）＜ε。

（3）对A∈∑，称A关于π是正则的，如果A关于π既是内正则的又是外正则的。

若对任意A∈∑，都有A关于π是正则的，则称集值模糊测度π是正则的。

注由定义可知：所有开集都是外正则的；所有闭集都是内正则的。

定理4设（Ω，∑，π）是上自连续的集值模糊测度空间，则集值模糊测度π是正则的充分必要条件为：对任意的A∈∑，∀ε＞0，都有X中的闭集F∈和开集G∈，使得F⊆A⊆G且δ（π（G-F），{}）＜ε。

证明必要性：如果π是正则的，则π既是内正则的又是外正则的。由定理3，∀ε＞0，∃δ＞0，当∀A，B∈∑，δ（π（A），{}）＜δ且δ（π（B），{}）＜δ时，有δ（π（A∪B），{}）＜ε。对上述δ＞0，有X中的闭集F∈和开集G∈，使得F⊆A，A⊆G且δ（π（A-F），{}）＜δ，δ（π（G-A），{}）＜δ。于是

充分性可由定义1（2）集值模糊测度的单调性直接得出。

为了证明集值模糊测度π的正则性，先讨论有关正则性的部分性质。

命题1设（Ω，∑，π）是上自连续的集值模糊测度空间，则：

（1）可数个外正则集的并集仍为外正则集；

（2）可数个外正则集的交集仍为外正则集。

证明（1）设{An}（n≥1）是一列外正则集。

∀ε＞0，由于A1是外正则的，存在G1∈，使得A1⊆G1且δ（π（G1-A1），{0}）＜ε/22。对于A2，存在G2k∈，使得A2⊆G2k且δ（π（G2k-A2），{}）＜1/k，k=1，2，…。于是当k→∞时，有π（G2k-A2）→{}。由于π是上自连续的，所以存在k0，使得当k≥k0时，

∀ε＞0，由定理3，∃δ＞0，当∀A，B∈∑，δ（π（A），{}）＜δ且δ（π（B），{}）＜δ时，有δ（π（A∪B），{}）＜ε。对上述δ＞0，存在充分大的m使得。同时由于是外正则的，所以存在G∈，使得且，{}）＜δ。于是

引理1对A∈∑，则有：

（1）A关于π是外正则的充要条件为A的补集Ac是内正则的；

（2）A关于π是正则的充要条件为A的补集Ac是正则的。

证明（2）由（1）直接得到，因此，只要证明（1）。为此设A是外正则的，则∀ε＞0，∃G∈A，使得A⊆G且δ（π（G-A），{}）＜ε。则Gc∈，Gc⊆Ac，且δ（π（Ac-Gc），{}）=δ（π（G-A），{}）＜ε。由定义可知Ac是内正则的。同理，若Ac是内正则的，∀ε＞0，∃F∈，使得F⊆Ac且δ（π（Ac-F），{}）＜ε。则Fc∈，A⊆Fc，且δ（π（Fc-A），{}）＜ε由定义可知A是外正则的。

由命题1及引理1即得以下命题：

命题2设（Ω，∑，π）是上自连续的集值模糊测度空间，则：

（1）可数个内正则集的交集仍为内正则集，

（2）可数个内正则集的并集仍为内正则集。

定理5（正则性定理）设（Ω，∑，π）是上自连续的集值模糊测度空间，那么π具有正则性。

证明因为∑为X的开集生成的σ-代数，为证明该定理，只要证明:（1）X中任意一列开集的并集是正则的；（2）X中任意一列开集的交集是正则的；（3）X的两个开集之差是正则的。

为证（1）和（2），首先注意到开集都是外正则的。而对于Banach空间X，其任意开集可以表达为X中可数个闭集的并，而闭集都是内正则的，再由命题2知X中的开集也是内正则的，所以X中任意一个开集都是正则的，再由命题1及命题2知（1）和（2）成立。

为证（3），任取开集A和B，则A和B都是正则的。由引理1（2）知Bc正则。从而A-B=A∩Bc也正则，即（3）成立。

3　结语

文中在文献[4]所定义的集值模糊测度空间上定义了集值模糊测度的正则性。应用一些引理得到了有关正则性的一些性质，如可数个外正则集的交集、并集仍是外正则集，可数个内正则集的交集、并集仍是内正则集。从而利用这些性质证明了上自连续的集值模糊测度必是正则的。

[1]VIND K.Edgeworth-Allocations in an exchange economy with many traders[J].International Economic Review，1964，5：165-177.

[2]SUGENO M.Theory of fuzzy integrals and its applications[D].Tokyo：Tokyo Institute of Technology，1974.

[3]WANG Z.The autocontinuity of set function and the fuzzy integral[J].J Math Anal Appl，1984，99：195-218.

[4]GAVRILUT A.Non-atomicity and the Darboux property for fuzzy and non-fuzzy Borel/Baire multivalued set functions[J].Fuzzy Sets and Systems，2009，160：1308-1317.

[5]WU J，LIU H.Autocontinuity of set-valued fuzzy measures and its applications[J].Fuzzy Set and Systems，2011，175（1）：57-64.

[6]GAVRILUT A.Regularity and autocontinuity of set multifunctions[J].Fuzzy Sets and Systems，2010，161：681-693.

[7]肖依，王贵君.集值模糊测度空间上可测函数列的收敛性[J].黑龙江大学学报（自然科学版），2010，27（3）：346-350.

[8]张以欣，王贵君，周立群.集值模糊测度空间上的Egoroff定理[J].山东大学学报（理学版），2010，45（5）：69-73.

[9]张以欣.序集值模糊测度及其所刻画的可测函数[D].天津：天津师范大学，2011.

The regularity of set-valued fuzzy measures

GENG Xiaoni，WU Jianrong
（School of Mathematics and Physics，SUST，Suzhou 215009，China）

This paper defined the regularity of set-valued fuzzy measure in the set-valued fuzzy measure space, discussed some properties of the regularity and proved that the set-valued fuzzy measure of the autocontinuity from above must be regular.

set-valued fuzzy measure；autocontinuous from above；regularity

O159MR（2000）Subject Classification：28C15；28E10

A

1672－0687（2016）01－0023－04

责任编辑：谢金春

2013－11－18

国家自然科学基金资助项目（11371013）

耿晓妮（1990-），女，辽宁沈阳人，硕士研究生，研究方向：模糊分析。*

吴健荣（1963-），男，教授，博士，硕士生导师，E－mail：jrwu@mail.usts.edu.cn。