弱非完整系统的Lagrange对称性与守恒量

严斌，张毅

（1.苏州科技学院数理学院，江苏苏州215009；2.苏州科技学院土木工程学院，江苏苏州215011）

弱非完整系统的Lagrange对称性与守恒量

严斌1，张毅2*

（1.苏州科技学院数理学院，江苏苏州215009；2.苏州科技学院土木工程学院，江苏苏州215011）

研究弱非完整系统的Lagrange对称性与守恒量。首先，建立弱非完整系统对应的零次近似系统和一次近似系统的运动微分方程。其次，给出弱非完整系统的零次近似系统和一次近似系统的Lagrange对称性的定义与判据，并得到零次近似系统和一次近似系统的Lagrange对称性导致的守恒量的条件及其形式。最后，举例说明其结果的应用。

弱非完整系统；近似系统；Lagrange对称性；守恒量

自1918年，Noether[1]揭示了对称性与守恒量（第一积分）之间的内在关系后，利用对称性方法寻求动力学系统的守恒量，一直是诸多学者研究的课题。现今，对称性方法主要有：Noether对称性[1-3]，Lie对称性[4-9]，Mei对称性[10-14]等。通过对称性方法不但可以找到更多的守恒量，而且有助于更深入地了解力学系统的动力学性态。

1966年，Currie和Saletan[15]探讨了单自由度力学系统的等效Lagrange函数问题，并证明其存在守恒量。1981年，Hojman和Harleston[16]将结果拓展到一般多自由度系统。赵跃宇等[2]将等效Lagrange问题，即对应于某一个Lagrange函数的运动微分方程的每一个解都满足从另一个Lagrange函数得到的运动微分方程，称为Lagrange对称性。近年来，对于完整和非完整力学系统的Lagrange对称性与守恒量的研究已取得了一系列重要成果[17-25]。然而，研究还未涉及到弱非完整系统。

弱非完整系统是一类具有一些重要性质的特殊动力学系统[26-28]，有别于完整和非完整力学系统，主要在于其约束方程中含有小参数μ。文中通过对含小参数μ的项进行幂级数展开，得到弱非完整系统对应的近似系统。不仅简化了计算，还便于从侧面了解弱非完整系统的动力学性质。研究了弱非完整系统对应的近似系统的Lagrange对称性及其守恒量，进一步完善动力学系统的Lagrange对称性理论。

1　弱非完整系统的近似系统的运动微分方程

假设力学系统的位形由n个广义坐标qs（s=1，2，…，n）来确定，其运动受有g个双面理想线性弱非完整约束

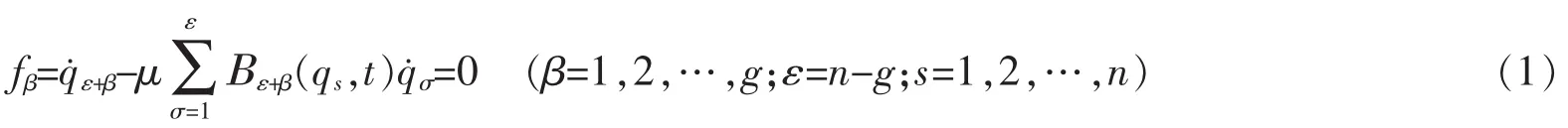
其中，μ为小参数。

系统的运动微分方程为

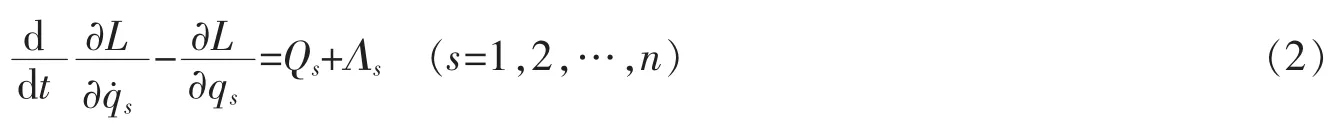
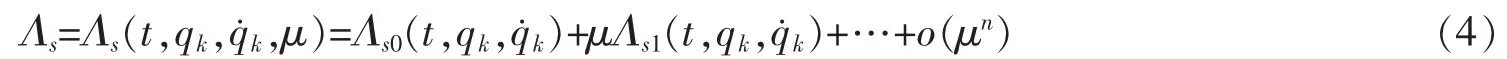
于是，弱非完整系统（2）的零次近似可以写成

一次近似为

式（5）和（6）可称为弱非完整系统（2）对应的零次近似系统和一次近似系统的运动微分方程。

2　Lagrange对称性的定义与判据

下面给出弱非完整系统对应的零次近似系统、一次近似系统的Lagrange对称性的定义与判据。

根据Λs对μ的幂级数展开式（4），给定弱非完整系统对应的零次近似系统的两组动力学函数L，Qs，Λs0和，令

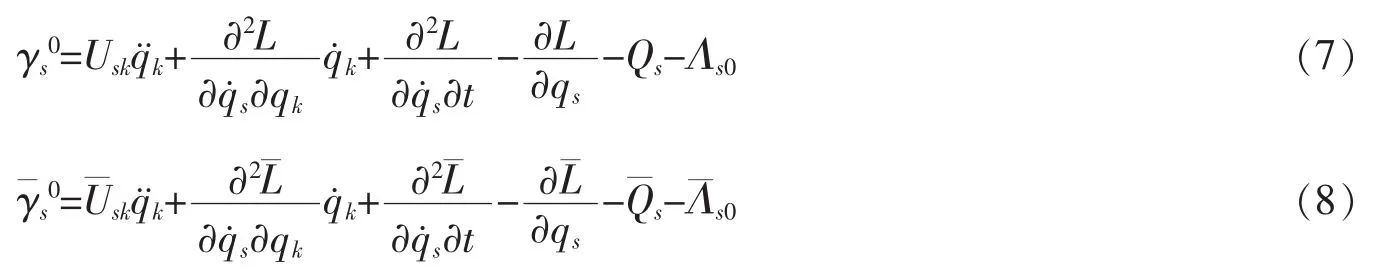
上标“0”代表零次近似。其中，

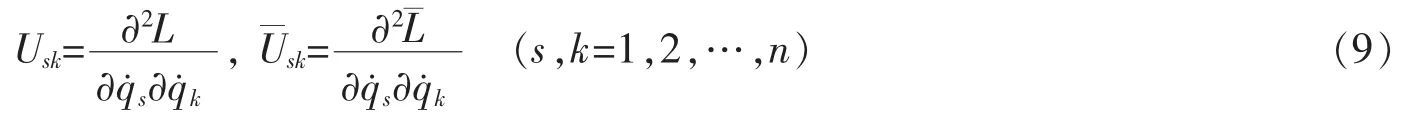
定义1对于弱非完整系统（1）和（2）相对应的零次近似系统（5），如果由动力学函数L，Qs，Λs0确定的运动微分方程

反之亦然，则相应不变性称为零次近似系统（5）的Lagrange对称性。

根据（8）和（11）式，得

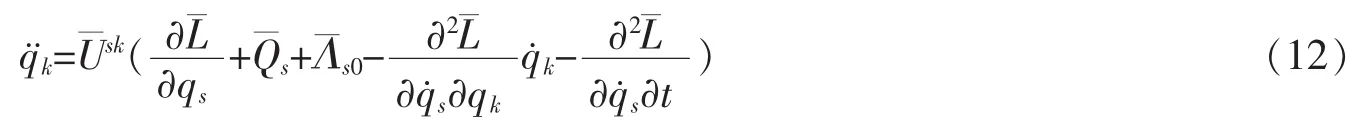
将（12）式代入（7）式，并根据方程（10）式，有

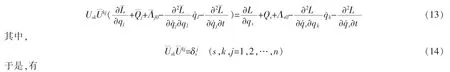
判据1对于弱非完整系统（1）和（2）相对应的零次近似系统（5），如果两组动力学函数L，Qs，Λs0和满足方程（13）式，则该零次近似系统（5）具有Lagrange对称性。

类似地，给定弱非完整系统对应的一次近似系统的两组动力学函数L，Qs，Λs0，Λs1和，令

上标“1”代表一次近似。因此，有

定义2对于弱非完整系统（1）和（2）相对应的一次近似系统（6），如果由动力学函数L，Qs，Λs0，Λs1确定的运动微分方程

反之亦然，则相应不变性称为该一次近似系统（6）的Lagrange对称性。根据方程式（15-18），有

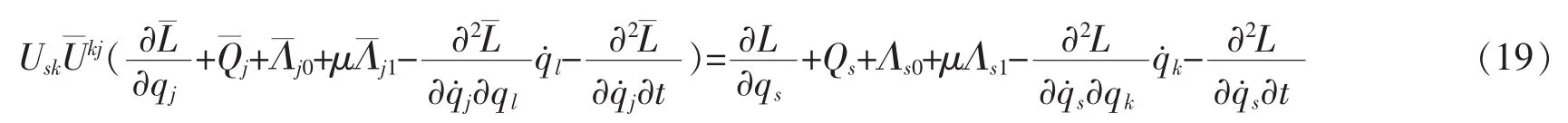
于是，有

判据2对于弱非完整系统（1）和（2）相对应的一次近似系统（6），如果两组动力学函数L，Qs，Λs0，Λs1和满足方程（19）式，则该一次近似系统（6）具有Lagrange对称性。

3　Lagrange对称性导致的守恒量

该节给出由弱非完整系统对应的零次近似系统、一次近似系统的Lagrange对称性导致的守恒量。若给出了关于μ的幂级数展开形式（4），并忽略含μ2的项以及更高阶小项。于是，有

定理1对于弱非完整系统（1）和（2）相对应的零次近似系统（5），如果两组动力学函数Qs，Λs0和满足条件

则该零次近似系统（5）的Lagrange对称性导致守恒量

其中，m为任意正整数。

证明类似于文献[21]中的推导过程，可以得到下列关系式

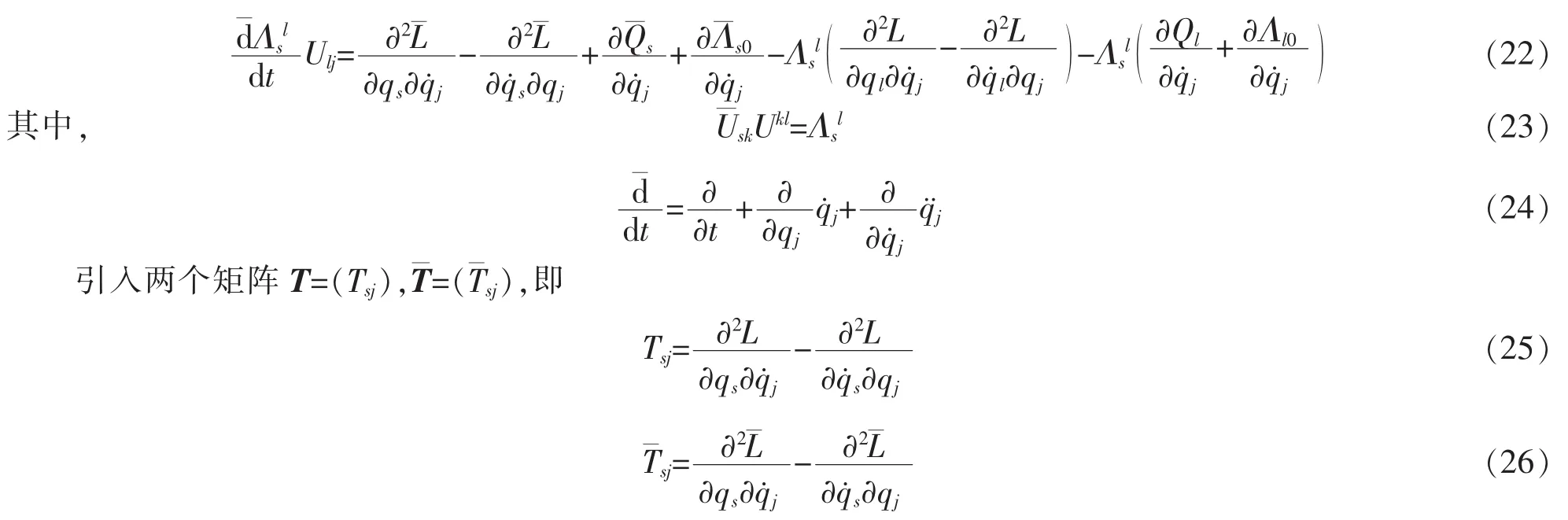
如果系统的动力学函数Qs，Λs0和满足如下条件

则方程（22）式可表示为矩阵形式

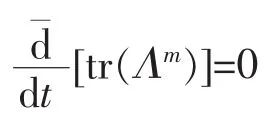
于是，有守恒量I

L=tr（Λm）=const.。证毕。

类似地，有

定理2对于弱非完整系统（1）和（2）相对应的一次近似系统（6），如果两组动力学函数Qs，Λs0，Λs1和满足条件

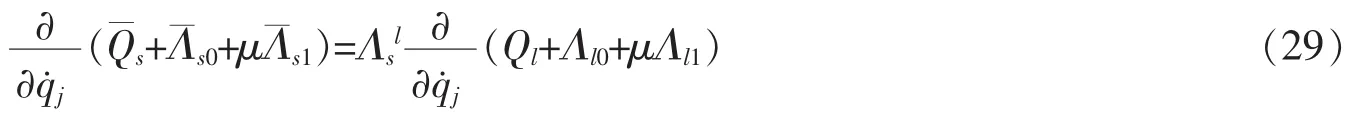
则该一次近似系统（6）的Lagrange对称性导致守恒量（21）。

4　算例

设一单位质量的质点在平面上运动，其系统的Lagrange函数为

下面研究弱非完整系统（30）-（32）相对应的零次近似系统、一次近似系统的Lagrange对称性及其相应的守恒量。

如果取

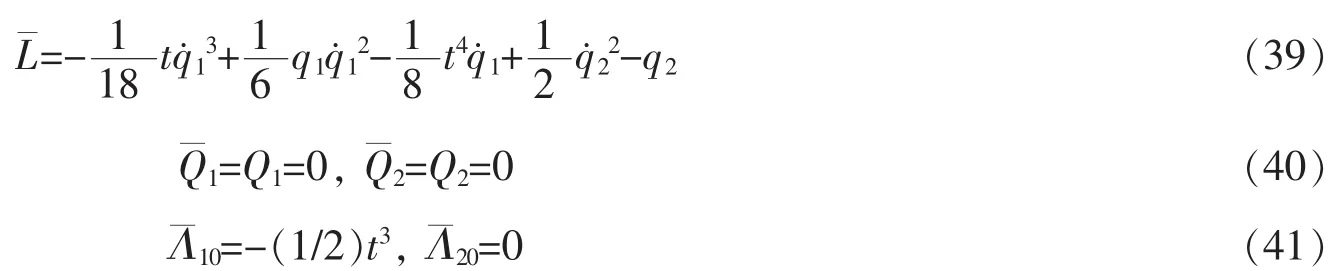
容易验证，（30）、（37）、（38）和（39）-（41）式满足关系式（13），根据判据1，相应的不变性为零次系统的Lagrange对称性，又由方程（23）式，可得

根据（42）式，容易验证函数组Qs，Λs和满足条件（20），则由文中的定理1，该系统存在如下守恒量

（43）式称为弱非完整系统对应的零次近似系统的Lagrange对称性导致的守恒量。

如果取

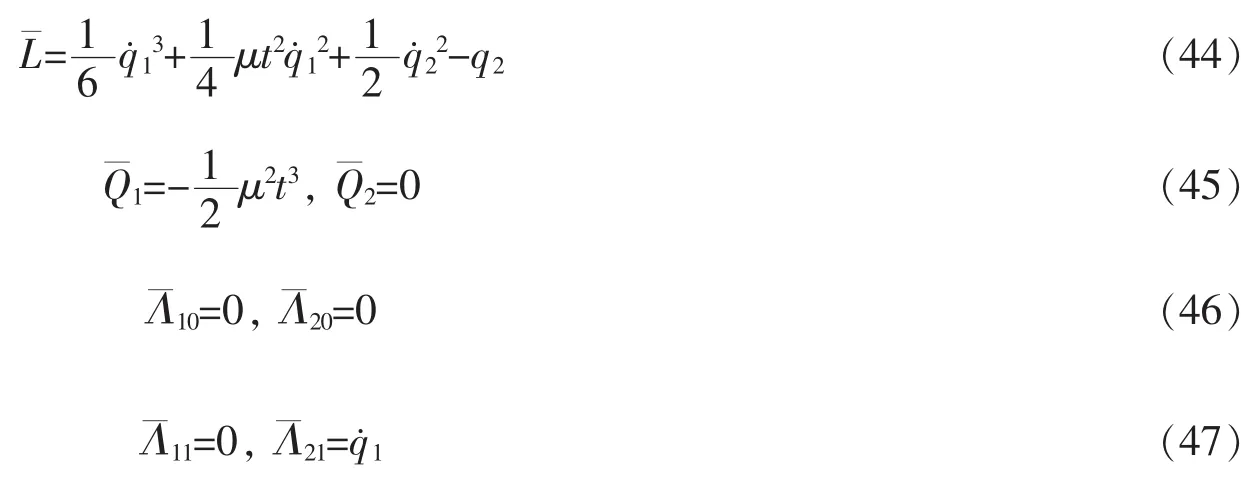
易证，（30）、（37）、（38）和（44）-（47）式满足关系式（19），据判据2，相应的不变性为一次近似系统的Lagrange对称性，根据式（23），得

根据（48）式，容易验证函数组Qs，Λs0，Λs1和满足条件（29），则由文中的定理2，该系统存在如下守恒量

（49）式称为弱非完整系统对应的一次近似系统的Lagrange对称性导致的守恒量。

5　结语

笔者研究了弱非完整系统对应的零次近似系统（5）和一次近似系统（6）的Lagrange对称性理论，得到了相应近似系统的Lagrange对称性的定义与判据，并根据Lagrange对称性给出了对应近似系统的守恒量的满足条件与形式。文中结果进一步完善了动力学系统的Lagrange对称性与守恒量理论。

[1]NOETHER A E.Invariante variationsprobleme[J].Nachr Akad Wiss G觟tt Math Phys，1918，Kl，II：235-257.

[2]赵跃宇，梅凤翔.力学系统的对称性与守恒量[M].北京：科学出版社，1999.

[3]梅凤翔.李群和李代数对约束力学系统的应用[M].北京：科学出版社，1999.

[4]LUTZKY M.Dynamical symmetries and conserved quantities[J].Journal of Physics A：Mathematical and General，1979，12（7）：973-981.

[5]LUTZKY M.Origin of non-Noether invariants[J].Physics Letters A，1979，75（1/2）：8-10.

[6]赵跃宇.非保守力学系统的Lie对称性和守恒量[J].力学学报，1994，26（3）：380-384.

[7]WU R H，MEI F X.On the Lie symmetries of the nonholonomic mechanical systems[J].Journal of Beijing Institute of Technology，1997，6（3）：229-235.

[8]张毅，薛纭.仅含第二类约束的约束Hamilton系统的Lie对称性[J].物理学报，2001，50（5）：816-819.

[9]ZHANG H B，CHEN L Q，GU S L.Lie symmetries and non-Noether conserved quantities of nonholonomic systems[J].Communications in Theoretical Physics，2004，42（3）：321-324.

[10]MEI F X.Form invariance of Lagrange system[J].Journal of Beijing Institute of Technology，2000，9（2）：120-124.

[11]WANG S Y，GE W K，MEI F X.Form invariance of motion equations of holonomic mechanical systems[J].Journal of Beijing Institute of Technology，2002，22（1）：20-22.

[12]罗绍凯.Hamilton系统的Mei对称性、Noether对称性和Lie对称性[J].物理学报，2003，52（12）：2941-2944.

[13]WU H B，XU X J，WANG S Y，et al.New Conserved quantity constructed upon form invariance for holonomic systems[J].Transactions of Beijing Institute of Technology，2004，24（6）：469-471.

[14]梅凤翔.约束力学系统的对称性与守恒量[M].北京：北京理工大学出版社，2004.

[15]CURRIE D G，SALETAN E J.q-Equivalent particle Hamiltonians.I.The classical one-dimensional case[J].Journal of Mathematical Physics，1966，7（6）：967-974.

[16]HOJMAN S，HARLESTON H.Equivalent Lagrangians：multidimensional case[J].Journal of Mathematical Physics，1981，22（7）：1414-1419.

[17]解加芳，梅凤翔.力学系统的Lagrange对称性[C]//中国数学力学物理学高新技术交叉研究学会第十二届学术年会论文集.北京：科学出版社，2008：45-48.

[18]MEI F X，WU H B.Symmetry of Lagrangians of nonholonomic systems[J].Physics Letters A，2008，372（13）：2141-2147.

[19]WU H B，MEI F X.Symmetry of Lagrangians of holonomic systems in terms of quasi-coordinates[J].Chinese Physics B，2009，18（8）：3145-3149.

[20]梅凤翔，吴惠彬.相对运动力学系统的Lagrange对称性[J].物理学报，2009，58（9）：5919-5922.

[21]张毅，葛伟宽.非Chetaev型非完整系统的Lagrange对称性与守恒量[J].物理学报，2009，58（11）：7447-7451.

[22]WU H B，MEI F X.Symmetry of Lagrangians of nonholonomic systems of non-Chetaev's type[J].Chinese Physics B，2010，19（3）：030303.

[23]WU H B，MEI F X.Symmetry of Lagrangians of a holonomic variable mass system[J].Chinese Physics B，2012，21（6）：064501.

[24]张斌，方建会，张克军.变质量非完整系统的Lagrange对称性与守恒量[J].物理学报，2012，61（2）：021101.

[25]张斌，方建会，张东爱，等.相对论性非完整系统的Lagrange对称性与守恒量[J].动力学与控制学报，2014，12（2）：105-110.

[26]梅凤翔.弱非完整系统的运动方程及其近似解[J].北京理工大学学报，1989，9（3）：10-17.

[27]梅凤翔.弱非完整系统的正则变换[J].科学通报，1992，37（13）：1180-1183.

[28]梅凤翔.一类弱非完整系统的稳定性[J].北京理工大学学报，1995，15（3）：237-242.

Lagrange symmetry and conserved quantity for a weakly nonholonomic system

YAN Bin1，ZHANG Yi2
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Civil Engineering，SUST，Suzhou 215011，China）

This paper mainly investigated Lagrange symmetry and conserved quantity for a weakly nonholonomic system.Firstly,we provided the differential equations of motion for the zero-order approximate system and the first-order approximate system corresponding to the weakly nonholonomic system.Secondly,we offered the definitions and criteria of Lagrange symmetry for the zero-order approximate system and the first-order approximate system of the weakly nonholonomic system.Then the conditions under which the Lagrange symmetry leads to a conserved quantity were deduced and the form of the conserved quantity was obtained.Finally,an example was given to illustrate the application of the results.

weakly nonholonomic system；approximate system；Lagrange symmetry；conserved quantity

O316MR（2000）Subject Classification：70H33；70F25

A

1672－0687（2016）01－0017－06

责任编辑：谢金春

2015－04－07

国家自然科学基金资助项目（10972151；11272227）

严斌（1989-），男，江苏兴化人，硕士研究生，研究方向：力学中的数学方法。*

张毅（1964-），男，博士，教授，博士生导师，E－mail：zhy@mail.usts.edu.cn。