改进Terminal滑模永磁直线同步电机控制策略研究*
2016-10-26余海涛李忠坤徐鸣飞
程 帆, 余海涛, 李忠坤, 徐鸣飞
(东南大学 电气工程学院,江苏 南京 210096)
改进Terminal滑模永磁直线同步电机控制策略研究*
程帆,余海涛,李忠坤,徐鸣飞
(东南大学 电气工程学院,江苏 南京210096)
永磁直线同步电机(PMLSM)作为一种高阶非线性系统,需要通过优化的控制算法来实现伺服系统的高精度和快速响应。非线性控制理论对于非线性系统有较好的控制性能,其中Terminal滑模控制相比较于传统滑模控制,具有收敛精度高的特点,并保留了滑模控制的鲁棒性。分析了PMLSM的数学模型,设计了基于非奇异Terminal位置滑模控制和一个一阶速度滑模面,通过二者的组合实现速度限幅和位置的精确响应。通过MATLAB/Simulink的仿真,结果表明,该方法下的PMLSM的改进Terminal滑模控制具有较高的控制精度和较快的响应速度,在存在外部扰动的情况下也具有较好的鲁棒性。
永磁直线同步电机; 磁场定向控制; 矢量控制; 非奇异Terminal滑模控制
0 引 言
以无铁心永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)为代表的直驱型伺服系统,相比较传统的滚珠丝杠式间接驱动,具有精度高、响应快、结构简单等优势,是数控机床加工的主要发展方向。为了克服直线电机所存在的端部效应及周期性波动等干扰因素,实现高精度的控制,目前研究主要集中在以两电平逆变器为基础,以矢量控制和直接转矩控制为代表的控制策略的改进上。其中包括了基于μ理论的鲁棒重复控制[1]、基于x域重复控制[2]、基于H∞鲁棒控制和零相位误差跟踪控制器[3]、基于二阶滑模的PMLSM调速系统[4]、模糊控制[5]等控制策略,以及基于干扰观测器的控制结构[6]。其中,滑模控制由于鲁棒性好、响应速度较快等特点,在PMLSM控制中得到了广泛应用。
由于滑模控制存在的抖振问题和传统滑模面存在收敛精度有限的问题,本文在这些文献的基础上,设计了一种改进的Terminal滑模控制策略。结合了Terminal滑模快速响应的特点,并使用辅助速度滑模面实现速度的限幅输出,简化了位置-速度环控制器的结构设计。在此基础上,MATLAB/Simulink的仿真结果表明,在给定位置较小的情况下,Terminal滑模控制器可以实现位置给定的快速响应并有较高的精度;在位置信号给定较大时,通过速度滑模面可以实现速度的限幅输出。从而证明了该结构滑模控制器可以在实现定位精度和响应速度提高的基础上,简化控制器的结构。
1 PMLSM的模型和矢量控制策略
相比较于有铁心结构或者单边PMLSM,双边无铁心PMLSM具有力能指标高、体积小及推力波动小等诸多优势,是直驱型高精度数控机床的主要发展方向[7]。在一般的永磁直线电机d-q轴数学模型中,令永磁体基波励磁磁场轴线为d轴,q轴为顺运动方向超前90°电角度的轴线。在三相绕组完全对称、磁场沿气隙正弦分布的前提下,可以得到表贴式(面装式)永磁直线电机的电压矢量方程:
(1)
式中:ud、uq——直轴和交轴电压分量;
Rs——电枢绕组的等效电阻;
Ld、Lq——直轴和交轴电感;
ωe——电角速度值;
Ψf——永磁体在电枢绕组中的磁链值;
p——微分算子。
PMLSM电磁推力和机械运动的表达式则为
(2)
式中:Fe——电磁推力;
Kf——电磁推力常数;
iq——q轴电流;
M——PMLSM动子和负载的等效质量;
v——运动速度;
B——粘滞摩擦因数;
F——由于电机参数变化以及外界扰动和非线性摩擦力所造成的扰动量。
2 Terminal滑模改进矢量控制策略
一般的PMLSM的矢量控制策略中,包含位置-速度-电流三闭环。通常在直轴和交轴电流环采用PI控制器,可以获得较快的响应速度。在位置- 速度控制器设计时,采用了一种基于改进之后的Terminal滑模控制器结构,可以实现动子的精确定位和速度的限幅输出[8]。具体为采用非奇异Terminal滑模面设计位置滑模控制器,并使用一阶滑模面设计辅助的速度滑模控制器,在实现精确定位的基础上可以实现速度的限幅输出。
2.1Terminal位置滑模控制器的设计
由PMLSM的电磁推力方程,并设给定位置信号为pr,动子反馈的位置信号为p,位置误差为x1,x1的一阶导数为x2。满足式(3)所示:
(3)
由电磁推力方程式可得到关系式:
(4)
式中:u——控制量,u=iq。
设计Terminal滑模面S,满足[9]:
(5)
式中:β>0,p、q满足1
设计滑模器的输出u满足:
(6)
其中:

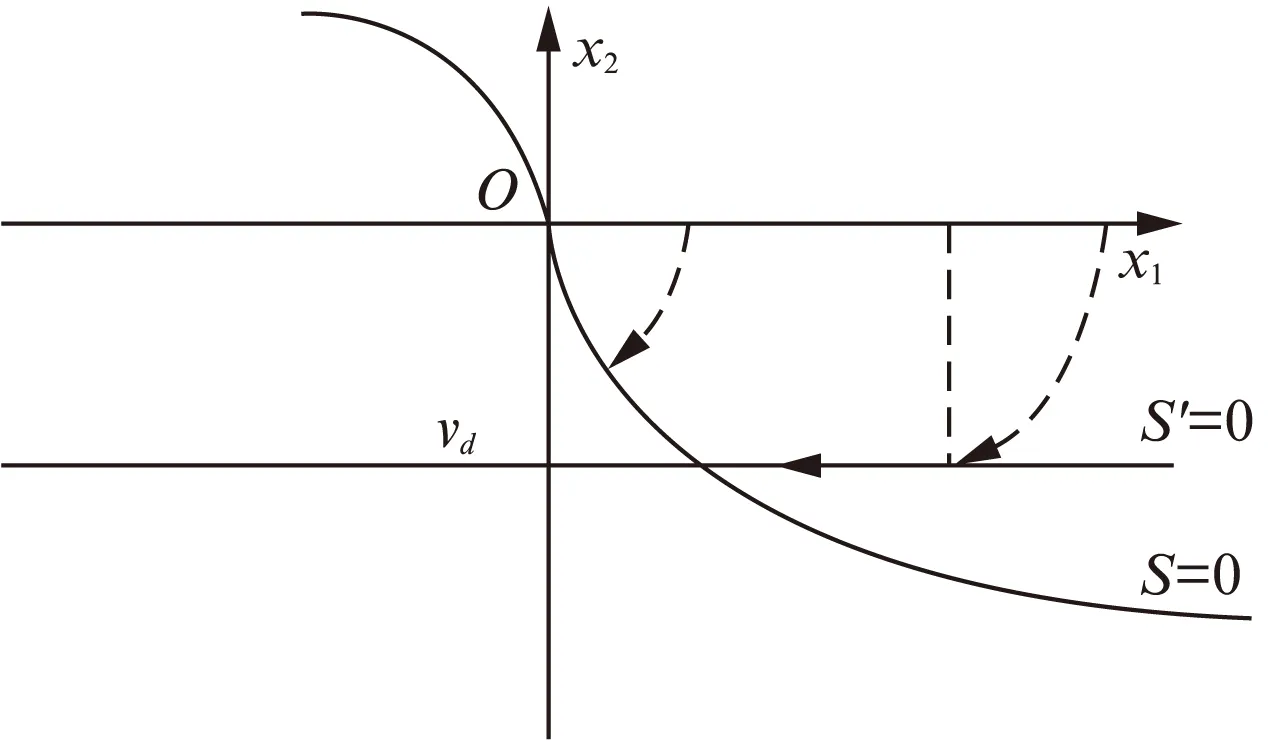
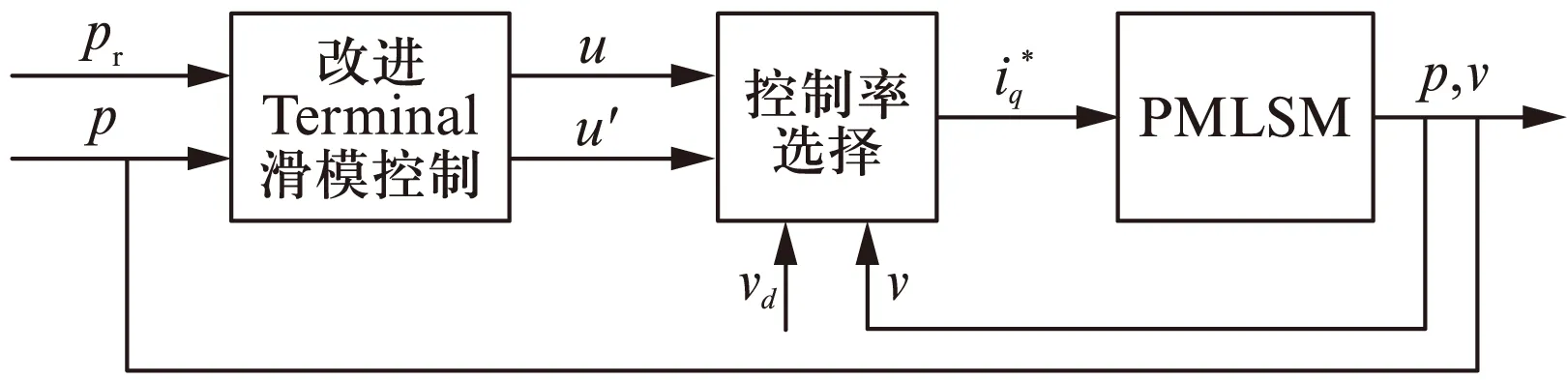
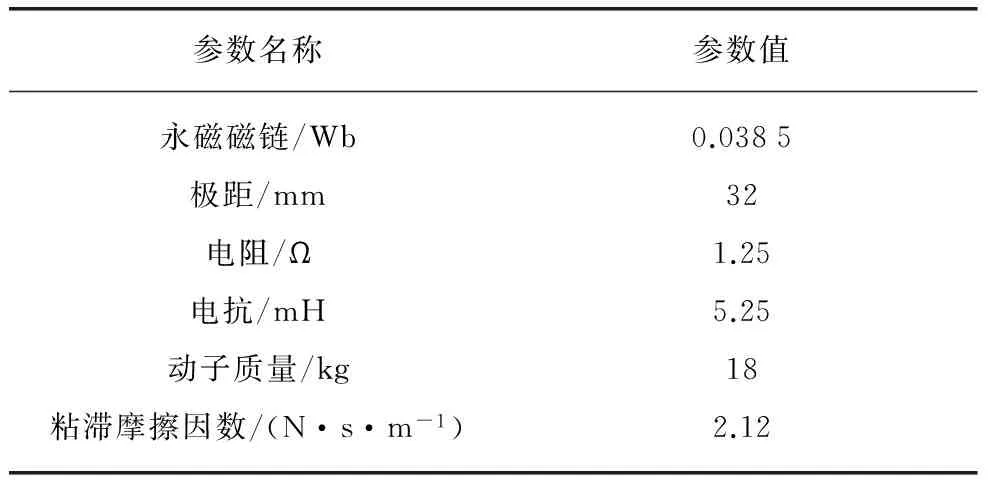
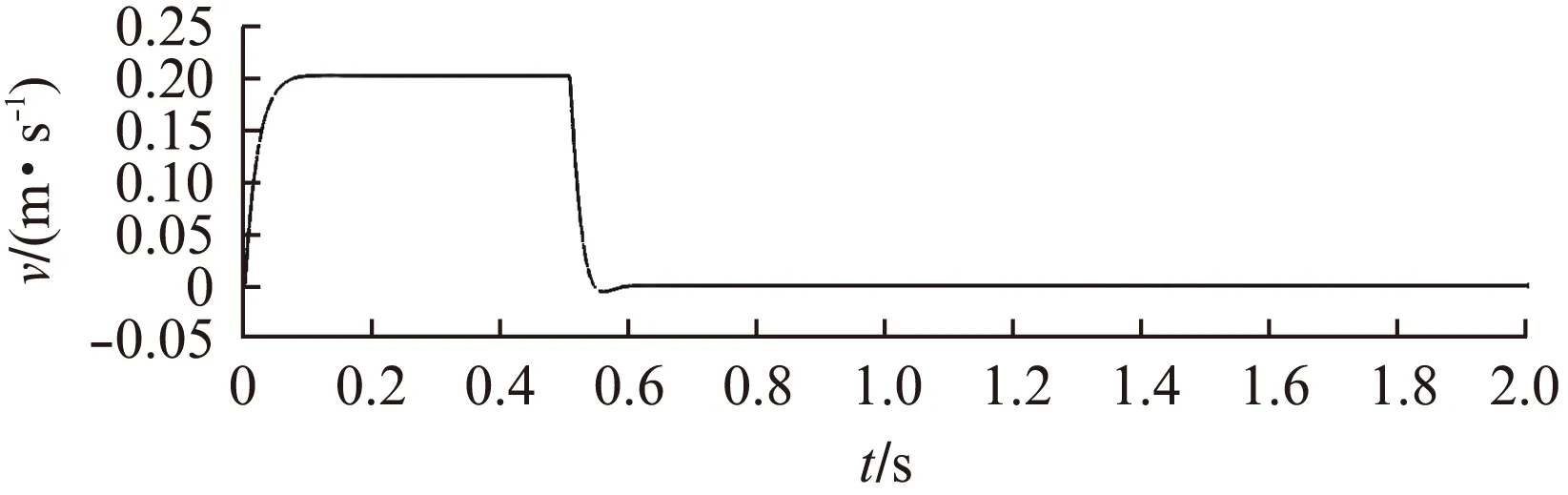
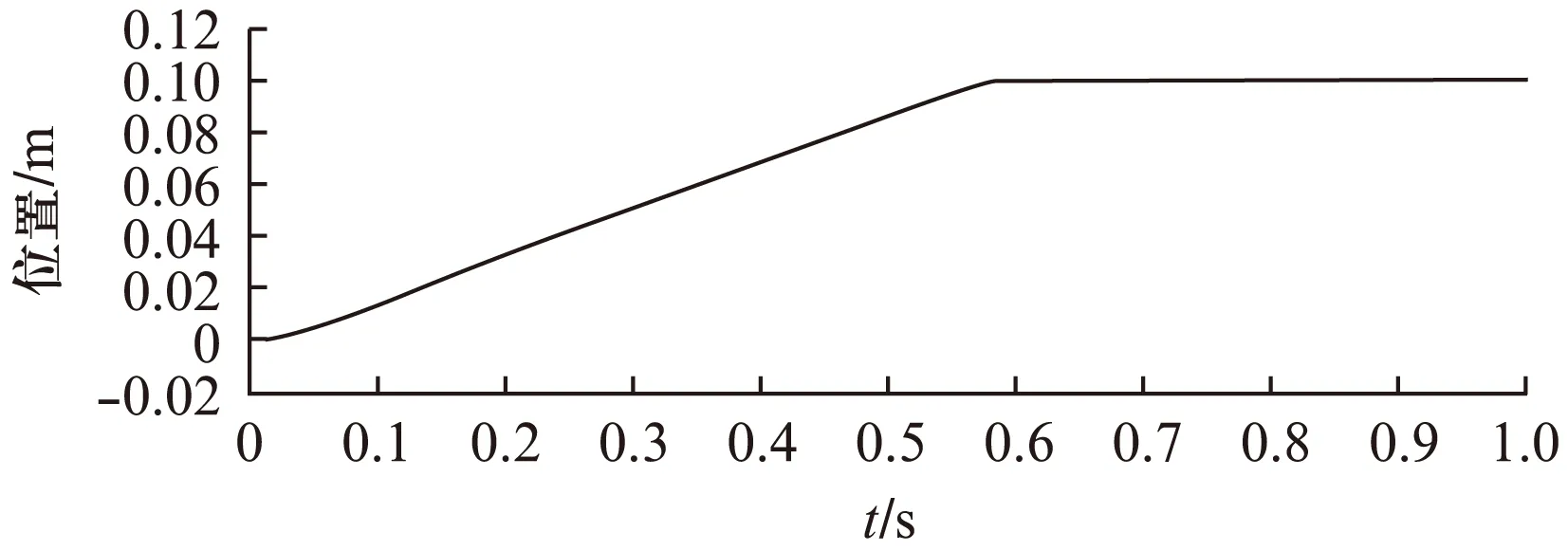
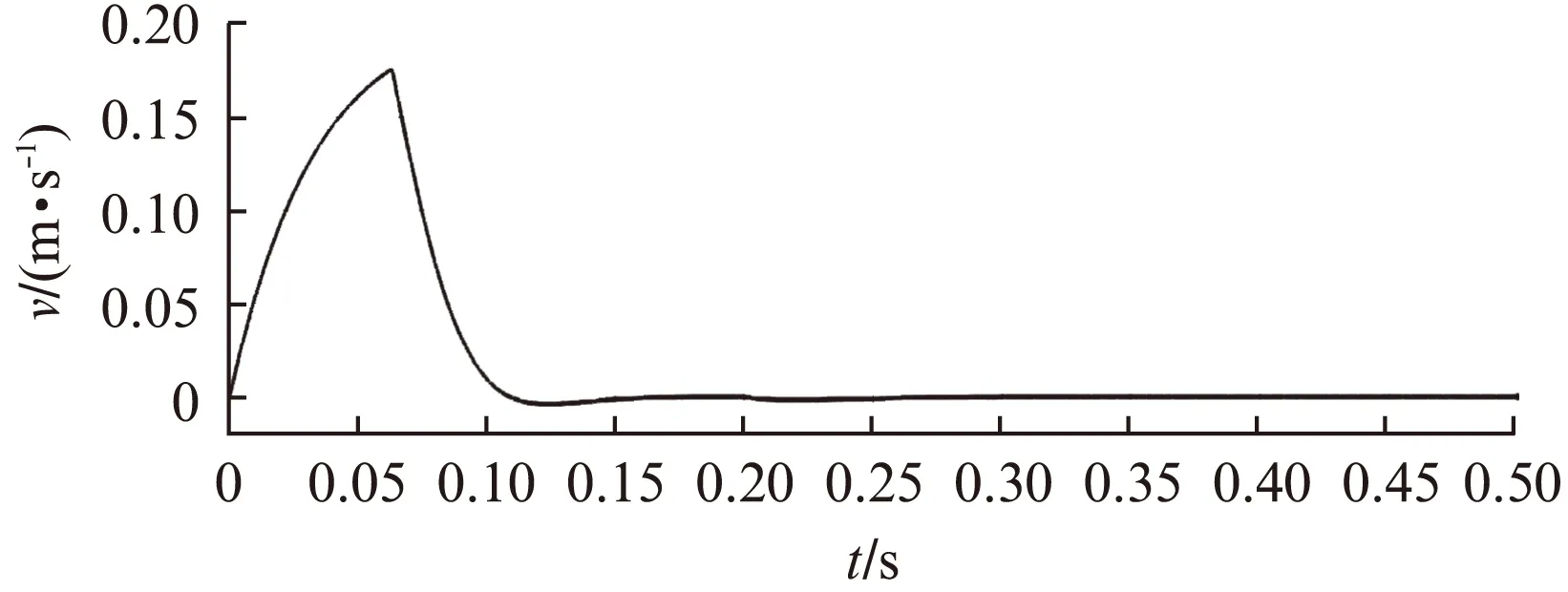
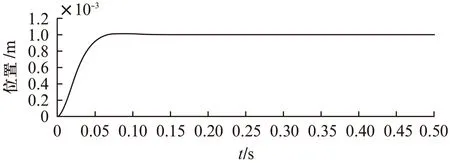
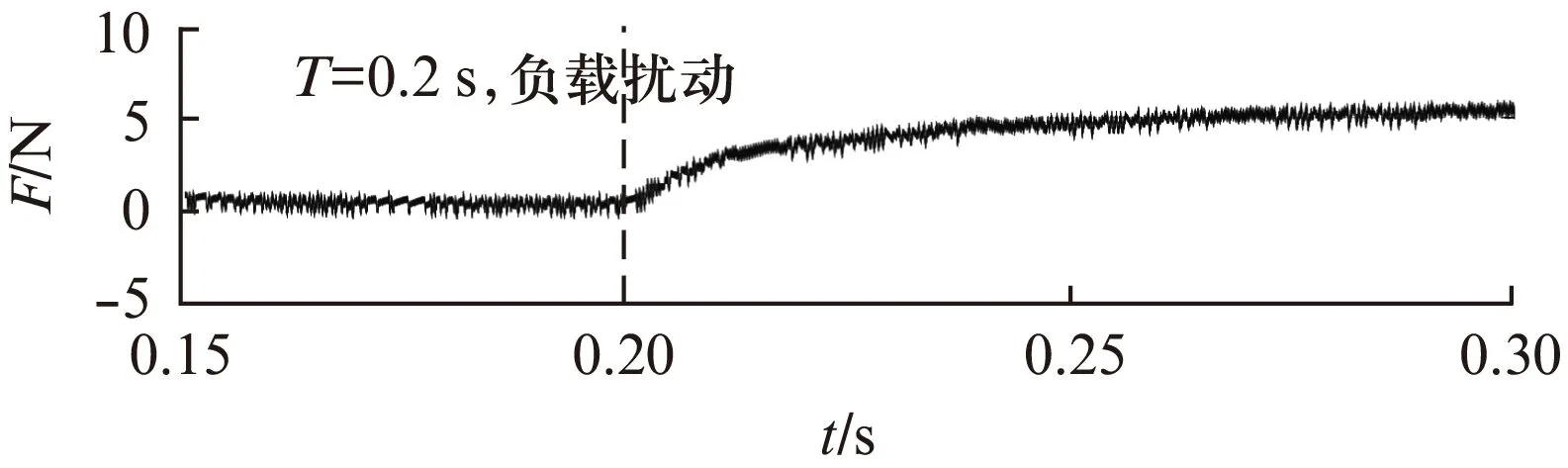
若假设扰动量F满足关系式|F| k>b|l/M| 那么可以证明该控制率满足Lyapunov稳定性。 选择Lyaponov函数: (7) 可以证明Lyapunov稳定性如下: 满足Lyapunov稳定性条件。 Terminal位置滑模控制器的结构如图1所示。 图1 Terminal滑模控制器结构 图1中,pr为位置输入给定量,p为位置反馈量。通过引入Terminal滑模位置控制器,即在原系统中引入新的闭环控制。通过选择合理的滑模面增益和其他参数,使得滑模控制器的输出满足Lyapunov稳定性,并在保持鲁棒性的基础上实现较短时间内收敛。 2.2辅助速度滑模控制器的设计 速度滑模面S′设计为 (8) 其中:vd=-vmax,vmax为动子的速度限制幅值。 由此可得到速度滑模的控制率: u′=φ3+φ4x2 (9) 可以证明Lyapunov稳定性如下: 满足Lyapunov稳定性条件。 2.3位置伺服系统的设计 选定速度滑模面和位置滑模面后,可分析系统的运行相轨迹,分为两种情况进行讨论。不同情况下的运行相轨迹如图2所示。 图2 系统运行相轨迹 当参考位置较小时,系统可直接到达位置滑模阶段,沿着位置滑模面S运动到原点达到稳定;当相对参考位置较大时,系统由初始状态首先到达速度滑模阶段,沿着速度滑模面S′运动到S和S′交点之后,再沿着位置滑模面S运动到原点达到稳定。 如图2所示,在系统起动加速阶段使用电流内环进行限幅,实现快速平稳起动。当经过起动加速,电机速度达到速度限幅值vmax时,系统进入速度滑模控制阶段(相对参考位置较小时不经历该阶段),保证电机按vmax平稳运行。当系统运行至速度滑模面S′=0和位置滑模面S=0的交点时,进入位置滑模控制阶段,在该阶段系统沿位置滑模面S=0做滑模运动。 当初始状态不在位置滑模面S上时,设tr为到达滑模面S的时间。当到达位置滑模面,即满足条件: 可以解得从初始状态到最终状态x1(ts)=0的时间[10]: 证明当运动到位置滑模面之后,在有限时间内可以达到收敛,从而相比一般的滑模控制具有更高的控制精度。采用的改进Terminal滑模控制器的总体结构如图3所示。 图3 改进Terminal滑模控制器结构图 仿真PMLSM采用无铁心结构,详细参数如表1所示。 表1 无铁心直线电机的参数 根据表1中的电机参数,在MATLAB/Simulink中构建整个控制系统的模型进行仿真。分以下三种情况进行验证。 (1) 情况1: 在位置给定为0.1m、速度限幅值vmax给定为0.2m/s情况下,位置给定,速度响应和位置响应结果如图4、图5所示。 图4 情况1下速度响应曲线 图5 情况1下位置响应曲线 (2) 情况2: 在位置给定为0.01m、速度限幅值vmax给定为0.2m/s情况下,位置给定,速度响应和位置响应结果如图6、图7所示。 图6 情况2下速度响应曲线 图7 情况2下位置响应曲线 综合比较上述两种情况,当位置给定信号较小时(情况2),系统直接由初始速度为0的状态通过Terminal位置滑模面S运动到给定位置;当位置给定信号较大时(情况1),系统初始速度为0的状态首先运动至滑模面S′状态,在该滑模面上实现了v=vmax的速度限幅输出,在到达S′和S交界点之后,通过Terminal位置滑模面S减速到给定位置收敛。 (3) 情况3: 考虑在位置给定为0.1m、速度限幅值vmax给定为0.2m/s情况下,在T=0.2s时负载出现扰动,三相电流和电磁推力如图8、图9所示。 图8 三相电流波形 图9 电磁推力波形 从图8、图9可看出,在快速起动之后电流波形很快稳定,当外部施加负载扰动之后,电流波形和电磁推力很快趋于稳定,证明了该控制策略具有较好的鲁棒性。 本文针对PMLSM伺服系统,结合非奇异Terminal滑模控制,构建了一种新的伺服控制策略。通过非奇异Terminal滑模在有限时间内收敛和一阶速度滑模对于速度的限幅输出作用,可以实现速度的限幅输出和位置的高精度响应。使用MATLAB/Simulink对该系统进行了不同位置给定信号和存在负载扰动下的仿真。仿真结果证明该方法可以在速度限幅的基础上,实现控制器结构的简化,并具有较强的鲁棒性。 [1]孙宜标,闫峰,刘春芳.基于μ理论的永磁直线同步电机鲁棒重复控制[J].中国电机工程学报,2009,29(30): 52-57. [2]孟高军,余海涛,黄磊,等.基于x域重复控制的磁通切换永磁直线电机定位力抑制方法[J].中国电机工程学报,2015,35(16): 4224- 4231. [3]曲永印,赵希梅,郭庆鼎.基于零相位误差跟踪控制器的轮廓误差交叉耦合控制[J].中国机械工程,2006,17(11): 1135-1137. [4]陆华才,徐月同,杨伟民,等.永磁直线同步电机进给系统模糊PID控制[J].电工技术学报,2007,22(4): 59-63. [5]孙宜标,杨雪,夏加宽.基于二阶滑模的永磁直线同步电机的鲁棒速度控制[J].电工技术学报,2007,22(10): 35- 41. [6]李志军,刘成颖,孟凡伟,等.基于ZPETC和DOB的直线电机控制器设计及实验研究[J].中国电机工程学报,2012,32(24): 134-140. [7]王昊,张之敬,刘成颖.永磁直线同步电机纵向端部效应补偿方法[J].中国电机工程学报,2010,30(36): 46-52. [8]姜长生,吴庆宪,费树岷.现代非线性系统鲁棒控制基础[M].哈尔滨: 哈尔滨工业大学出版社,2012. [9]张前,黄学良,周赣.永磁同步直线电动机的位置滑模控制器设计[J].微特电机,2010,38(5): 53-55. [10]LI S, ZHOU M, YU X. Design and implementation of terminal sliding mode control method for PMSM speed regulation system[J]. IEEE Transactions on Industrial Informatics, 2013,9(4): 1879-1891. Research of Improved Terminal Sliding Mode Control of Permanent Magnet Linear Synchronous Motor* CHENGFan,YUHaitao,LIZhongkun,XUMingfei (College of Electrical Engineering, Southeast University, Nanjing 210096, China) Permanent magnet linear synchronous motor(PMLSM) was considered as a high order nonlinear system. Thus, the optimization control algorithm was required to realize the high precision and fast response of servo system. Due to the brilliant performance of nonlinear control theory, terminal sliding mode control was applied with high convergence precision and robustness. On base of mathematical model of PMLSM, non singular terminal position sliding mode control and a first order speed sliding mode surface was designed and combined to achieve speed limit and exact response of location. The MATLAB/Simulink simulation results showed that the method of PMLSM improved Terminal sliding mode control had high control precision, fast response and good robustness in the presence of external disturbances. permanent magnet linear synchronous motor(PMLSM); field-oriented control(FOC); vector control; non singular Terminal sliding mode control 国家自然科学基金项目(41576096) 程帆(1992—),男,硕士研究生,研究方向为直线电机伺服驱动控制。 TM 301.2∶TM 351 A 1673-6540(2016)08- 0031- 05 2016-03-09
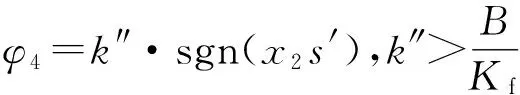

3 仿真及结果

4 结 语
