永磁同步电机参数自学习滑模控制研究*

唐红雨，　赵文祥

(1. 镇江市高等专科学校 电气与信息工程学院，江苏 镇江　212013；2. 江苏大学 电气信息工程学院，江苏 镇江　212003)



永磁同步电机参数自学习滑模控制研究*

唐红雨1，赵文祥2

(1. 镇江市高等专科学校 电气与信息工程学院，江苏 镇江212013；2. 江苏大学 电气信息工程学院，江苏 镇江212003)

在传统滑模控制中，通常根据实测电流和观测器的电流估计值之差设计滑模面，但这往往会造成趋近滑模面较慢和相位滞后问题。以电流和磁链作为RBF神经网络滑模观测器的输入，把转子角速度作为未知量，采用RBF神经网络最小参数自学习算法，使神经网络滑模控制器的输出作为系统位置控制输入信号，通过参数的估计代替网络权值的调整，减少了计算量，采用指数型趋近律有效降低滑模控制的抖振现象。通过与传统滑模仿真试验相比，比较结果表明该方法可以提高系统的响应速度，实现转子位置的准确估算，降低抖振，改善系统的动态性能。

永磁同步电机； 滑模控制； RBF网络； 参数自学习； 观测器

0　引　言

永磁同步电机(Permanent Magnet Synchronous Motor, PMSM)具有结构简单、体积小、动态响应快、过载能力强、易于调速等优点，具有非线性、多变量、强耦合等特点，国内外学者对PMSM的控制算法作了深入的研究[1-7]。但是高性能运行控制需要对永磁电机的转矩与磁链进行解耦，而电机参数随外界环境变化影响很大，存在大量负载扰动，使系统原定的解耦关系变化，造成系统控制精度下降[8]。

无传感器技术由于能简化系统结构、降低成本，已成为电机控制系统的研究热点。无传感器的参数辨识方法主要有高频信号注入法、MARS法、反电动势法、扩展卡尔曼滤波器法、滑模观测器法等[9]。相比较而言，滑模控制方法具有响应快、对参数变化和扰动不敏感、鲁棒性强、算法设计简单等优点，对于复杂非线性系统的控制具有广泛的应用前景。但传统滑模理论中的观测器易产生较大抖动，且存在采用低通滤波器提取连续反电动势时导致的相位滞后无法得到精确补偿等问题，使其应用受到限制[10- 11]；或者进行反馈线性化解耦控制[12]，利用高阶滑模算法的PMSM控制器，以降低抖动，提高系统的鲁棒性，但运算量增加[13]。在Terminal滑模控制方法中引入非线性函数，并与模糊控制相结合，但模糊算法本身的不确定性增加了滑模的抖动[14]。在滑模面的设计中引入积分项来解决稳态误差问题，将这种积分滑模面应用到PMSM控制器设计中，但积分项的加入会降低系统的动态性能[15-16]。滑模中运用反电动势法对无位置传感器PMSM系统的转子位置和速度进行辨识[17-18]。

本文考虑到PMSM在运行中会出现参数和负载扰动的情况，在传统滑模变结构控制方法的基础上，引入具有径向基函数(Radical Basic Function， RBF)最小参数自学习的滑模观测器，以电流作为输入量，通过自学习算法对转子角速度进行逼近学习，降低滑模观测器的抖振，实现PMSM的位置跟踪控制，使系统具有良好的鲁棒性和动、静态性能。

1　PMSM数学模型

PMSM在旋转坐标系下的数学模型如下：

(1)

式中：id、iq，ud、uq——电机的d、q轴电流和电压；

Rs——电机的定子电阻；

pn——电机的极对数；

ω——电机转子角速度，rad/s；

Ld、Lq——电机d、q轴的电感；

ψf——电机的永磁磁链；

J——电机的转动惯量，kg·m2。

对采用位置跟踪算法的表面式PMSM而言，其d、q轴电感相等，即Ld=Lq=L，PMSM在静止坐标系下的数学模型如下[19]：

(2)

(3)

2　基于RBF的滑模观测器设计

永磁电机位置角方程为

(4)

式中：θ——转子位置角，rad；

B——电机的黏性摩擦因数，N·m·s；

T1——电机扭矩，N·m。

在设计PMSM控制器时，考虑到RBF神经网络对系统参数的不确定性有着较好的自学习功能，可以实现对给定期望位置的准确跟踪控制，获得良好的动态特性[21-22]。本文以ψf、iα、iβ作为RBF神经网络的输入，网络的输出作为观测器的输入，采用RBF神经网络最小参数自学习[23]，只需要确定网络的核心参数权值、节点和核函数，可以减少计算量。选择滑模函数时必须考虑在滑模面上的快速性和抖振。这里控制器选择一阶线性滑模函数，相比于高阶、非奇异终端滑模，其滑模阶数和滑模面自身的复杂性降低，如式(5)所示：

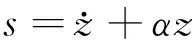
(5)

式中：α>0为常数。

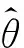
(6)

(7)

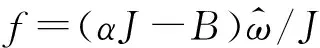
《现代汉语词典》里说：“诚实；规规矩矩”，算是“标准答案”。于我而言，倒更记得幼时老爷子对着识字读本对我中气十足的训诫：老实，就是守规矩。

g=pnψfiq/J

式中：g——已知非线性函数；

Tl/J——干扰项；

f——未知非线性函数；

iq、θ——输入和输出。

采用网络对不确定项f进行自适应逼近[22]，RBF网络逼近算法为

(8)

(9)

式中：is——网络的输入信号，即is=[iαiβ]T，电流iα、iβ由电流互感器检测三相定子电流经坐标变换求得；

cj、b——常系数；

j——网络隐含层节点的个数，这里定为4个节点；

W——神经网络权值；

h=[h1,h2,h3,h4]T——高斯函数的输出；

ε——神经网络逼近误差，ε≤|εm|。

采用RBF网络逼近f，输出为

(10)

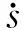
设计iq控制律为

(11)

负载转矩作为干扰项反馈到电流iq控制律中。当负载出现扰动时，控制器能及时对干扰作出响应，使系统具有较好的抗扰动效果。

滑模控制器实现方法如图1所示，k≥εm，μ>0，控制律代入式(7)，得

(12)

同理，得到转子角速度的控制律：

(13)

图1　滑模控制器结构图

三闭环系统结构图如图2所示。结构主要包括逆变器、电源整流器、电流控制器GACR、速度控制器GASR和位置跟踪器GAPR。θ*、ω*为电机期望转子

图2　PMSM系统控制结构图

3　系统稳定性分析

为验证控制律的可行性和所设计的系统稳定性，定义Lyapunov函数为

(14)

对L求导，得

(15)

(16)

则：

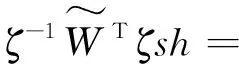
s[ε-ksgn(s)-μs]=

s[ε-ksgn(s)-μs]

(17)

4　仿真与试验

为验证控制方法的可行性，在MATLAB环境下进行仿真。PMSM的参数如下：PN=1.5kW，UN=380V，nN=1200r/min，IN=3.5A，pn=3，RS=2.875Ω，L=15mH，J=0.011kg·m2，B=0.01，Ψf=0.8Wb，逆变器开关频率为10kHz。滑模面参数如下：η=0.5，μ=20，ε0=0.0015，α=15，ε=1×10-4，m=4，ζ=0.05，b=0.50，cj=[1 0.5 0 0.5]。仿真时，对普通滑模控制和本方案控制的转速及负载变化进行跟踪比较。

(1) 负载转矩为1N·m保持不变，转速在0.3s从1200r/min降为800 r/min时，电流、转速、转矩的跟踪曲线如图3所示。

从图3可知，转速突变时，对于普通滑模控制，在转速突变瞬间波动大，超调明显，但本方案控制能够较快地跟踪，响应时间为0.015s，d、q轴电流在转速突变瞬间有波动，且q轴电流比d轴电流波动大，因为d轴电流接近于0，转矩在转速突变瞬间有一个峰值波动，但经过0.01s以后，转矩稳定。从图4可以看出，电机在0.3s转速突变时，能及时跟踪角度，且本方案控制比普通滑模控制的误差低、精度高，使滑模观测器的估算结果更平滑、准确。

(2) 负载转矩在0.3s从1N·m变为5N·m时，电流、转速、转矩的跟踪曲线如图5所示。

从图5可看出，当负载转矩在0.3s从1N·m变为5N·m时，普通滑模控制造成各个指标波动较大，尤其在起动瞬间。本方案能准确检测出转矩突变，d轴电流几乎无波动，q轴电流有所增加；受转矩变大的影响，电机转速突然降低，但仅经过0.15s就趋于稳定状态。

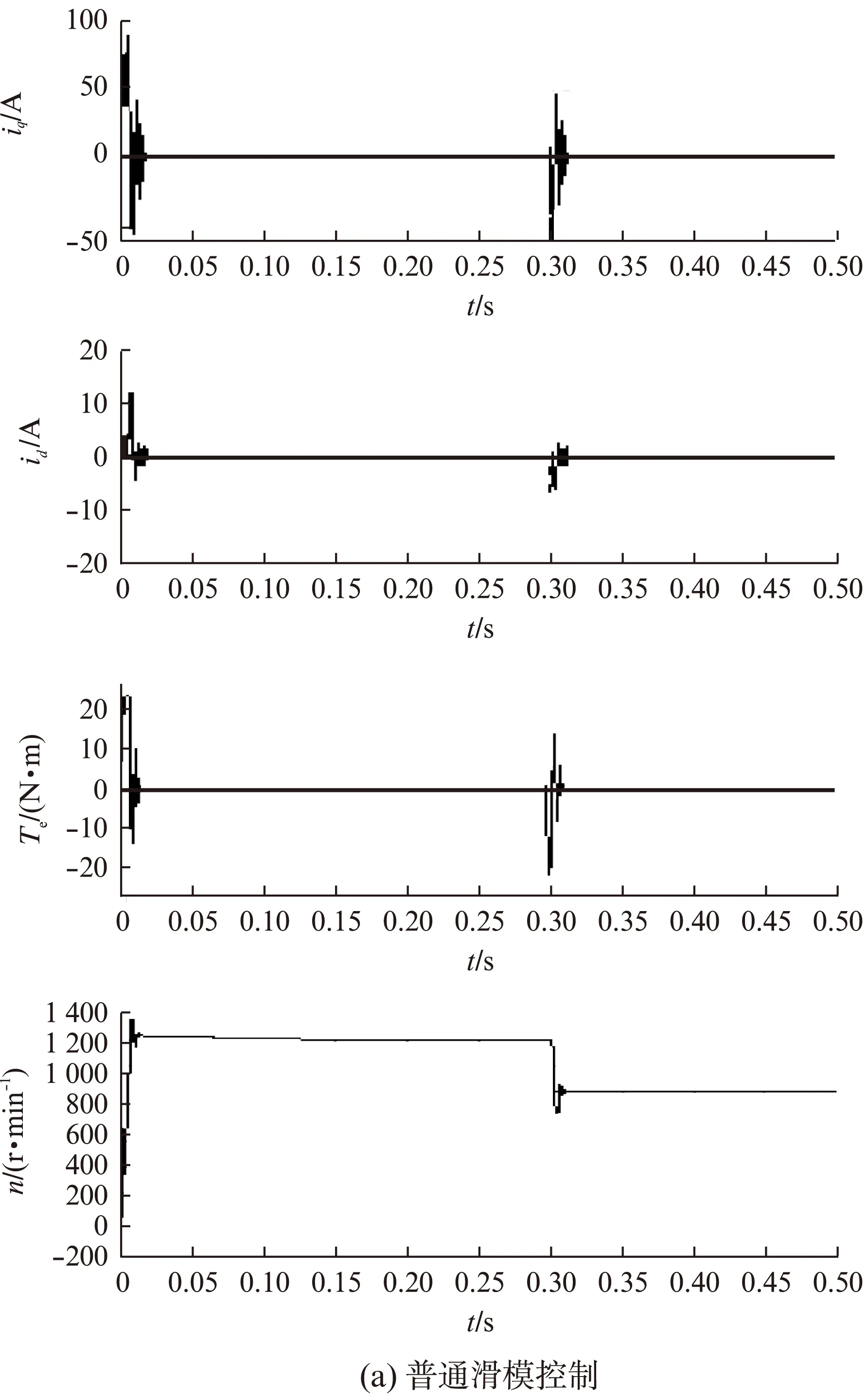
图3　转速变化时，电流、电磁转矩和转速跟踪曲线

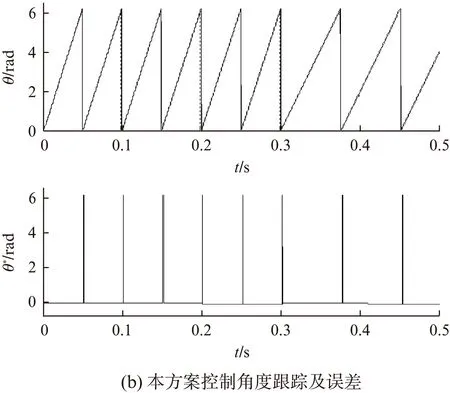
图4　角度跟踪对比

(3) 试验验证。为验证算法的可行性，在实验室搭建了电路，主要器件如下： 核心芯片DSP2812，三菱IPM(PM150CVA060)，2048线的光电编码器，2kW的直流电机做负载，还有扭矩传感器、LEM型电流传感器。试验结果如图6所示。

图6为普通滑模控制和本方案控制起动时的转速实测波形，给定转速为600 r/min，相比本方案控制，普通滑模控制转速存在较大的超调，而由于存在参数的自学习，本方案的起动调节时间短。

图7给出了两种控制方案下，电磁转矩Te的试验波形。在普通滑模控制下，Te输出存在抖振，而基于RBF最小参数自学习的滑模控制，利用参数逼近和指数型趋近率使切换增益减少，Te抖振现象下降，提高了系统的稳定性。

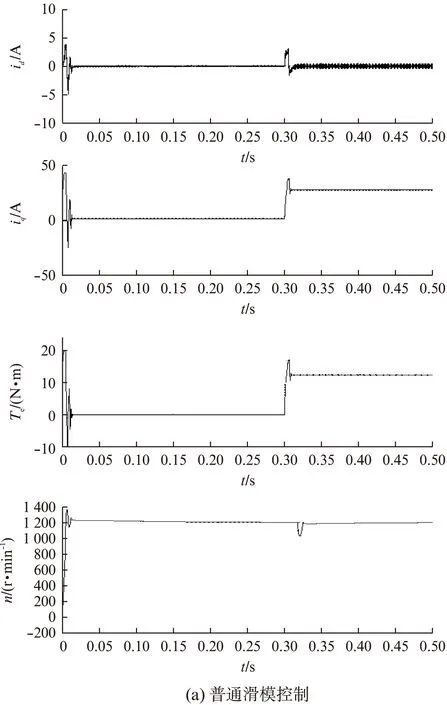
图5　负载转矩突变时，电流、电磁转矩、转速响应曲线

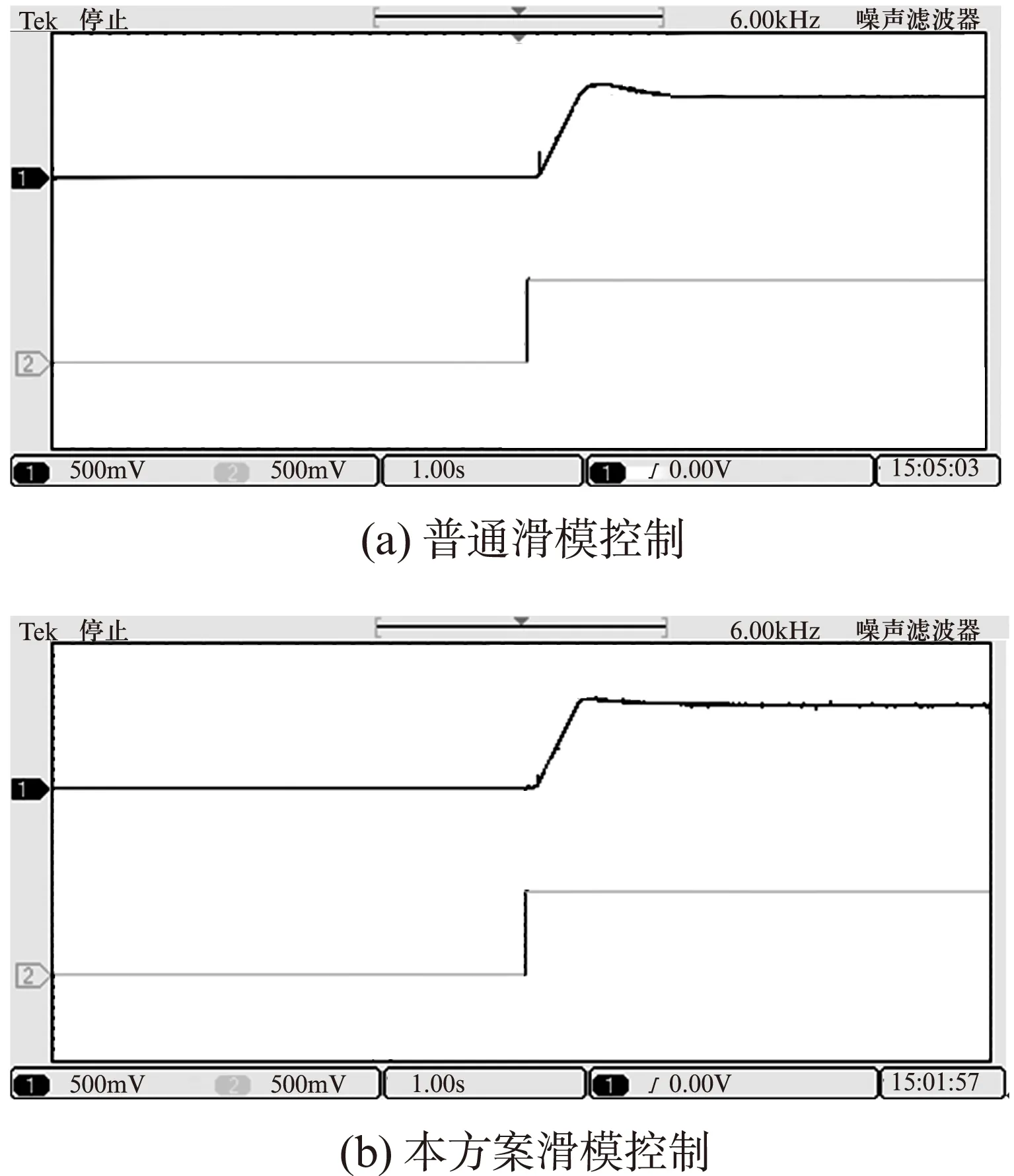
图6　起动时的转速跟踪曲线

图7　转矩输出波形

5　结　语

综上分析，在电机加入负载、转速突变时，采用RBF神经网络最小参数自学习的滑模观测器方法不需要低通滤波器，简化了结构。通过网络权值的估算代替权值调整，网络自学习逼近算法推算出电机转子角速度，从而得到转子位置角，转子位置跟踪及时，使控制系统的估算精度提高；当负载转速、转矩发生变动时，能准确跟踪速度、转矩信号，采用逼近算法对未知项逼近，使系统具有较好的鲁棒性。试验证明本方案的滑模控制比传统滑模控制更能降低系统抖动，使系统具有较好的动态性能。

[1]杨代利，张宏立.基于全鲁棒滑模控制的永磁同步电机伺服系统矢量控制[J].电机与控制应用，2014，41(2)： 11-13.

[2]纪艳华，钱佳利.基于DSP和FPGA的全数字永磁同步电机伺服系统的设计[J].电机与控制应用，2014，41(3)： 28-31.

[3]张海燕，刘军，兖涛，等.永磁同步电机在全速范围内的无位置矢量控制[J].电机与控制应用，2014，41(7)： 1-5.

[4]刘芳璇，王桂荣.基于自适应模糊微分积分滑模的无速度传感器永磁同步电机运行研究[J].电机与控制应用，2014，41(9)： 7-11.

[5]郑昌陆，胡月波，耿宇翔.基于锁相环原理的永磁同步电机无传感器控制方法[J].电机与控制应用，2015，42(3)： 24-28.

[6]李明，程启明，陈根，等.一种新型永磁同步电机滑模观测器设计方法[J].电机与控制应用，2015，42(6)： 1-5.

[7]高靖凯，林荣文，张润波.永磁同步电机直接转矩控制的研究及算法改进[J].电机与控制应用，2015，42(11)： 21-25.

[8]LEE H Y, LEE J Y. Design of iterative sliding mode observer for sensorless PMSM control[J].IEEE Transactions on Control Systems Technology,2013，21(4)： 1394-1299.

[9]ZHAO W Q, SHI T N, WANG Y D, et al. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor[J].IEEE Transactions on Industrial Electronics,2013,60(2)： 710-719.

[10]EL-SOUSY F F M. Robust wavelet-neural-network sliding-mode control system for permanent magnet synchronous motor drive[J].IET Electric Power Applications,2011，5(1)： 113-132.

[11]皇甫宜耿,LAGHROUCHE S,刘卫国,等.高阶滑模消抖控制在永磁同步电动机中的应用[J].电机与控制学报,2012，16(2)： 7-11.

[12]VU N T T, YU D Y, HAN H C. T-S fuzzy-model-based sliding-mode control for surface mounted permanent magnet synchronous motors considering Uncertainties[J]. IEEE Transactions on Industrial Electronics,2013，60(10)： 4281- 4291.

[13]KIM H, SON J, LEE J. A high-speed sliding-mode observer for the sensorless speed control of a PMSM[J]. IEEE Transactions on Industrial Electronics, 2011，58(9)： 4069- 4077.

[14]QI L, BAO S, SHI H. Permanent-magnet synchronous motor velocity control based on second-order integral sliding mode control algorithm[J]. Transactions of the Institute of Measurement and Control, 2015, 37(7)： 875-882.

[15]袁雷,沈建清,肖飞,等.插入式永磁低速同步电机非奇异终端滑模观测器设计[J].物理学报,2013，62(3)： 37- 45.

[16]钱荣荣,骆敏舟,赵江海,等.永磁同步电动机新型自适应滑模控制[J].控制理论与应用,2013，30(11)： 1414-1421.

[17]李毓洲,阳林.基于小波神经网络的永磁同步电机无速度传感器滑模控制[J].电机与控制应用，2010，37(3)： 53-56.

[18]卢涛,于海生,山炳强，等.永磁同步电机伺服系统的自适应滑模最大转矩/电流控制[J].控制理论与应用,2015，32(2)： 251-255.

[19]刘希,孙秀霞,董文瀚,等.无抖振离散滑模趋近律[J].控制与决策,2013，28(8)： 1277-1280.

[20]CORRADINII M L, IPPOLITI G, ORLANDOL G. A quasi-sliding mode approach for robust control and speed estimation of PM synchronous motors[J]. IEEE Transactions on Industrial Electronics, 2012，59(2)： 1096-1104.

[21]张晓光,孙力,赵克.基于负载转矩滑模观测的永磁同步电机滑模控制[J].中国电机工程学报,2012，32(3)： 111-116.

[22]FENG Y, YU X H, HAN F L. High-order terminal sliding-mode observer for parameter estimation of a permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2013，60(10)： 4272- 4280.

[23]WANG H Q, CHEN B, LIN C. Direct adaptive neural control for strict-feedback stochastic nonlinear systems[J]. Nonlinear Dynamics, 2012,67(4)： 2703-2718.

[24]LIU J K. Radial basis function (RBF) neural network control for mechanical systems[M]. Beijing: Tsinghua University Press，2013.

Sliding Mode Control Study for Permanent Magnet Synchronous Motor Based on Parameters Seal-Learning*

TANGHongyu1,ZHAOWenxiang2

(1. School of Electrical and Information Engineering, Zhenjiang College, Zhenjiang 212003, China；2. School of Electrical and Information Engineering, Jiangsu University, Zhenjiang 212013， China)

In the traditional sliding mode control, the new sliding mode surface was designed according to the difference between the measured and the observer-based estimated currents, which could cause to reach the sliding surface slowly and phase lag. The stator currents were taken as the input of the RBF neural network sliding observer, and the rotor angular velocity as unknown variables. Since the network minimal parameters learning algorithm was adopted, so that the neural network sliding controller output was regarded as the position control system input signal. Instead of the network weights adjustment by the parameters estimating, which reduced the amount of computation. Exponential reaching law was used to reduce the vibration of the system. Comparing with the traditional sliding mode through, the results verified that the proposed control method offered faster speed response, accurately estimating the rotor position, reducing buffeting and improving the dynamic performance.

permanent magnet synchronous motor(PMSM); sliding mode control; RBF network; parameters seal-learning; observer

国家自然科学基金项目(51477068)；江苏省自然科学基金项目(BK20130011)

唐红雨(1975—)，男，硕士，副教授，研究方向为特种电机非线性控制。

赵文祥(1976—)，男，博导，教授，研究方向为永磁电机及其控制系统研究。

TM 351

A

1673-6540(2016)08- 0001- 07

2016-02-26