基于现场可编程门阵列的永磁同步电机伺服系统*

邢天宇，　王孝洪，　田联房

(华南理工大学 自动化科学与工程学院，广东 广州　510640)



基于现场可编程门阵列的永磁同步电机伺服系统*

邢天宇，王孝洪，田联房

(华南理工大学 自动化科学与工程学院，广东 广州510640)

提出了一种基于Altera公司生产的现场可编程门阵列(FPGA)的永磁同步电机伺服控制系统的设计，运用了矢量变换、坐标变换等策略，使用了空间矢量脉宽调制(SVPWM)、 Cordic、 PID控制等技术，并以FPGA为主控制器将其实现。同时给出了系统的整体结构，最后利用PWM逆变器对系统进行试验验证，试验结果印证了理论的正确性，证明系统有良好的性能。

现场可编程门阵列； 矢量控制； 永磁同步电机； 伺服系统

0　引　言

制造业是国家经济的支柱，而其中伺服系统的性能在制造业中起了很关键的作用。生活中，伺服系统也扮演了极为重要的角色[1]。家用电器、汽车、电子类，或是其他相关产品，都和伺服系统息息相关。因此，国内外都十分重视伺服系统的探索与研究。

当前伺服系统的主要研究方向是在交流永磁同步电机的平台上研究伺服系统，同步电机性价比很高，低速时的性能也较为优越[2]。为了更好地控制永磁同步电机，研制相对简单高效的控制系统一直是重中之重。

近年来，随着技术的革新，电子设计自动化(Electronic Design Automatic, EDA)技术一直在发展和进步，现场可编程门阵列(Field Programmable Gate Array， FPGA)芯片的性能也有了提升。甚至很多新的算法也可以通过FPGA来实现[3]。与其他的控制芯片相比，FPGA更加快速稳定，也有更好的可重构性。FPGA用硬件描述语言，以硬件的方式来控制各个脚的输出，比软件程序具有更好的稳定性，因此把FPGA作为主要控制芯片来控制伺服系统的优势是巨大的。

本文以Altera公司的FPGA芯片EP4CE30F23 C8为核心，搭建了双闭环控制系统和硬件试验平台，最后通过试验验证了其有效性。

1　基本原理

1.1电机矢量控制原理

永磁同步电机的控制策略有很多，使用最广泛并且最有效的是矢量控制策略。其工作原理是通过坐标变换，将三相系统等效为两相系统，再经过旋转坐标变换实现对定子电流的解耦[4]，以达到电动机的磁链和转矩分开控制的目的。

一般定义电流矢量为

(1)

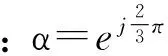
综上所述，首先进行Clark变换，结果为

(2)

再经过Park变换，结果为

(3)

式中： θ——变换角度。

在变换后的坐标系下，电压方程为

(4)

其中：

(5)

式中： R——定子电阻；

q——微分环节系数；

ω——角速度；

φd、φq——d、q轴磁通分量；

φf——定子磁通。

Park变换后的电磁转矩为

(6)

保持id=0，则

(7)

由此可见，实现了励磁和转矩的分开控制，达到了解耦的效果。

1.2空间矢量脉宽调制

空间矢量脉宽调制(Space Vector Pulse Width Modulation， SVPWM)技术在交流电机变频驱动中有着很重要的应用。其通过不同的开关组合[5]，来跟踪实际的磁链圆。SVPWM技术具有很好的最大电压利用率，同时线性调节性能也相当优越。

图1所示三相逆变器的8个开关状态分别为U0(000)、U1(100)、U2(110)、U3(010)、U4(011)、U5(001)、U6(101)、U7(111)。其中1表示对应的那一相上桥臂导通，下桥臂关断；0则相反，表示下桥臂导通，上桥臂关断。

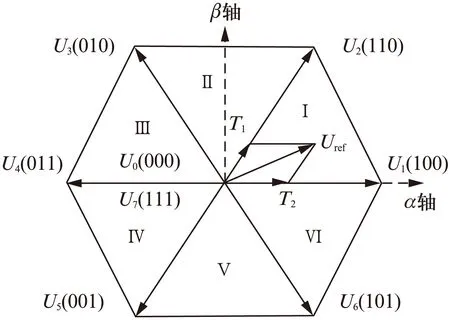
图1　三相逆变器的8个开关状态

在实际运行中，通过三相逆变器[6]的8个开关状态去模拟幅值不变的旋转矢量。根据Urefα,Urefβ来计算矢量所在哪个扇区，确定需要合成的目标矢量，同时计算相应的占空比，最终得到需要输出的PWM信号。

1.3Cordic算法

在Park变换中，坐标旋转需要用到大量的三角函数计算，采用的是Cordic算法[7]。Cordic算法具有结构简单、速度快等优点，更容易在FPGA中实现。

当θ∈[-π,π]时，在圆周坐标系中Cordic算法的迭代公式为

i=0,1,2,…,n-1

(8)

迭代初始值为

(9)

定义符号函数如下：

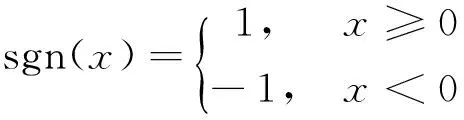
(10)

迭代足够多次时：

(11)

1.4PI控制器

控制器是系统中非常重要的环节。选用PI控制器主要出于易于实现、较为可靠的原因[8]。PI控制器在工业制造其他领域也有着比较广泛的应用。

PI控制器可以表示为

PI(n)=PI(n-1)+Kp[e(n)-

e(n-1)]+Kie(n)

(12)

式中：Kp——比例环节增益；

e(n)——误差输入；

Ki——积分环节增益。

1.5 M/T速度测量器

目前广泛使用的测速方法，主要有测量频率方法和测量周期方法两种[9]。M法是对频率进行测量，测量一定时间下的脉冲数目，换算成对应的频率。T法是对周期进行测量，测量两个脉冲之间间隔的时间单位，把它换算成周期。

M法和T法各自有各自的缺点： M法中，测量的一开始和末尾会可能存在半个脉冲的影响，会有误差，从而在高速的条件下性能较好；而周期方法，首尾会存在半个时间单位的影响，会有1个单位的时间误差，从而适合测量低速。

在这里选用了M/T测速法[10]，就是在对反应转速n的脉冲计数的同时，也对脉冲个数的时基脉冲进行计数。

此时的转速可以表示为

(13)

式中：f0——时基脉冲频率；

P——每转产生的脉冲个数；

m1、m2——测量开始到结束这段时间内的反应转速的脉冲数和时基脉冲个数。

2　系统模块实现

2.1Cordic模块

图2　Cordic模块流程图

2.2SVPWM模块

SVPWM模块主要由定标运算、扇区判断、矢量分配、时间计算、死区调节等子模块组成。如图3所示。图3中，模块的输入是Uα，Uβ信号；Init为初始化信号；Ctrl为控制信号，控制系统的状态，比如运行在故障保护、故障清除等状态[12]；Mode为模式选择，0时是不对称模式，1时是对称模式；N为开关频率设置值；Dead-time为死区时间设置值。设定开关频率为16kHz，死区时间为0.8μs。

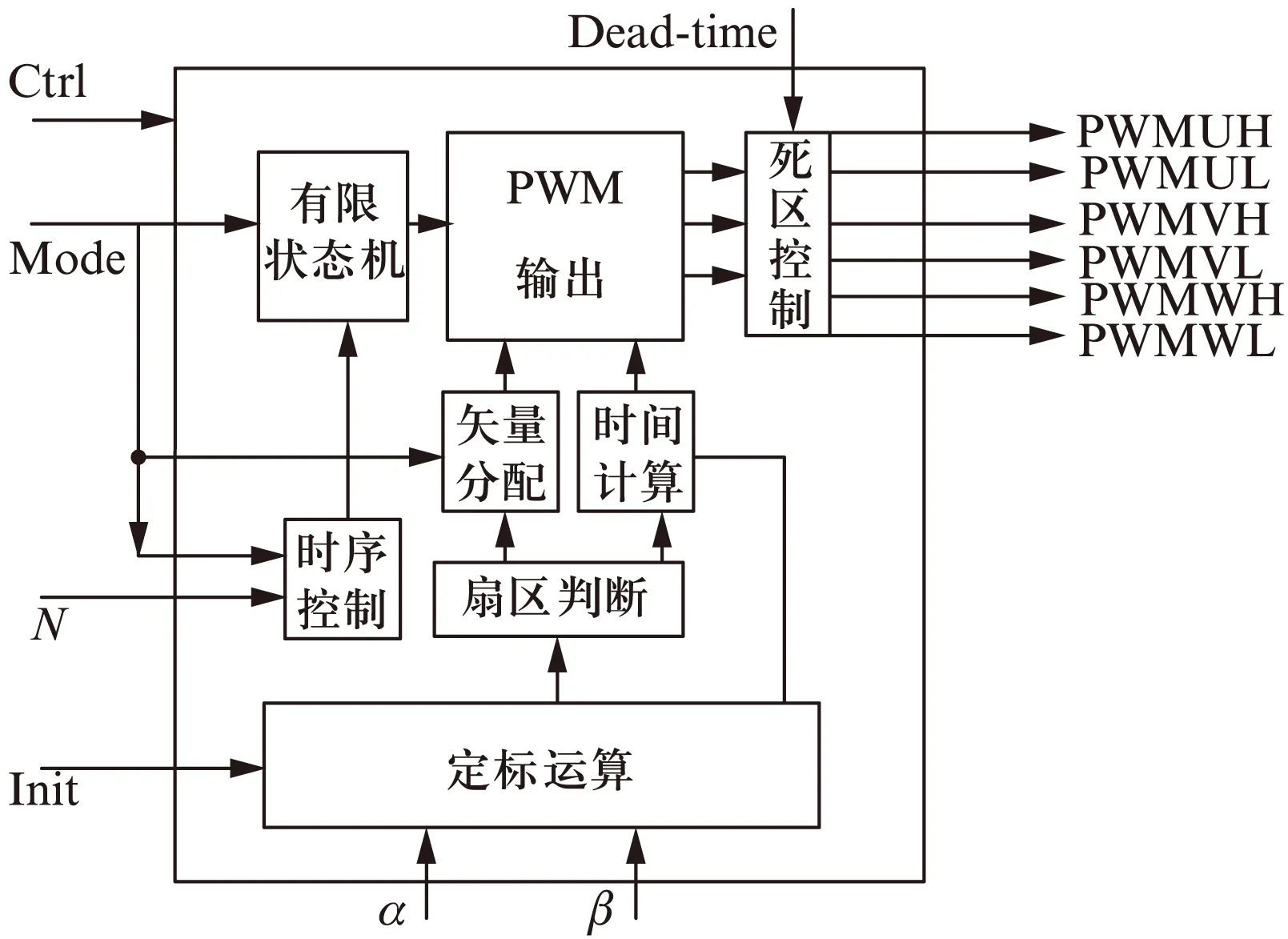
图3　SVPWM模块

2.3PI控制器的实现

PI模块结构如图4所示，其中用到了抗积分饱和的方法。当参考值较大时，积分器有可能建立一个很大的误差值[13]，这个误差值在积分的惯性作用下将要维持一段时间，从而导致很大的超调。因此，在输出饱和时立刻关闭积分作用，即可减少对超调的影响。

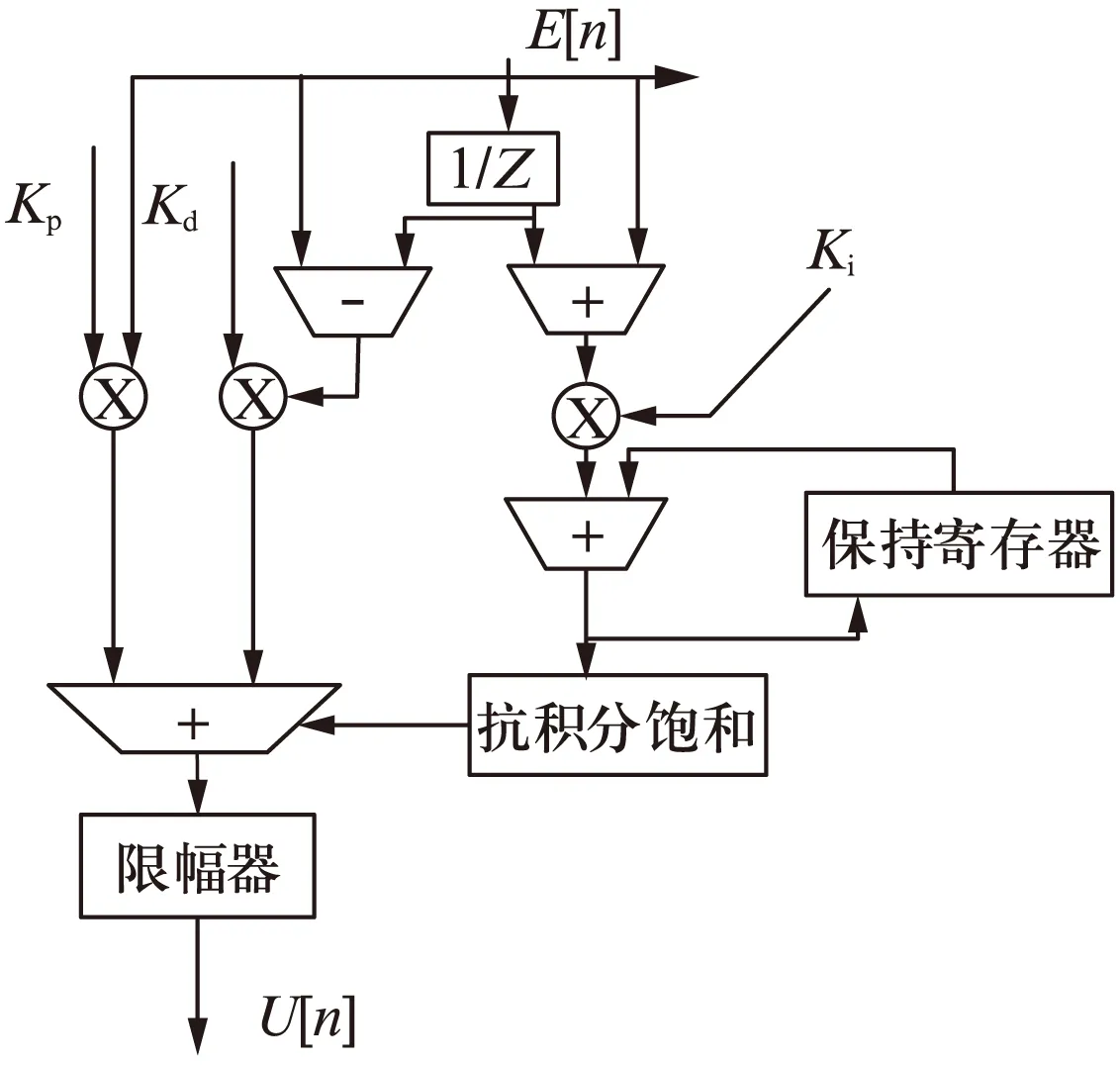
图4　PI控制器

3　系统硬件结构

系统主电路采用交直交的方案。先是通过二极管整流得到直流母线电压[14]；再通过控制板上

的FPGA来控制PWM逆变器；控制系统同时还具有过压过流保护的功能，保证系统的安全运作。控制电路采用Altera公司的FPGA芯片EP4CE30F23C8作为控制器，通过霍尔元件和光电编码器测得相电流值和转速[15]，以上文提到的方式进行坐标变换，并将得到的电压空间矢量PWM信号发送给驱动电路，驱动电路驱动IGBT的开关管[16]。系统的硬件结构框图如图5所示。

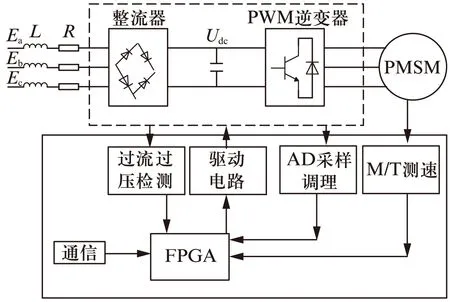
图5　系统的硬件结构图

4　试验验证

对本文设计的系统进行试验验证，使用Quartus 13.0进行编译及综合后，逻辑单元共占用58%。使用前面描述的平台进行试验，根据器件特性选取开关管的频率为10kHz，使用的永磁同步电机参数如下： 定子电阻Rs=4.256Ω，定子电感Ls=0.3713H，极对数为2对，额定电流5A，额定转速1500r/min，额定功率2.2kW。

图6表示SVPWM输出给驱动电路的实时信号。由图6可见这符合预期的估计。经过二极管整流的母线电压Udc、实际的相电流Ia，还有此时的变换角度θ如图7所示。Udc为三相电经二极管整流而来，变换角度θ不断周期变化，其变化的频率也表征了系统的速度。运行在约25Hz，即约750r/min；同时，θ角的频率和Ia的频率一致，Ia约为2A。

图6　SVPWM输出给驱动电路的实时信号

图7　直流母线定子电流和变换角度

实际的转速阶跃响应如图8所示。从图8中可以看出，给了目标750r/min的速度命令之后，其稳态误差小于1%，超调量的最大值小于5%，响应时间不到1ms，因此具有良好的动态性能。

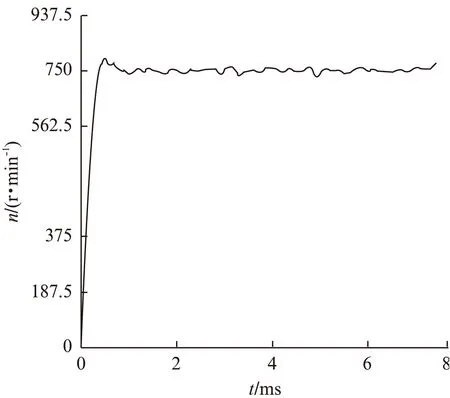
图8　转速阶跃响应

5　结　语

基于FPGA的交流永磁同步电机伺服系统是当前领域的主流趋势，具有高性价比和低速时的优越性能。本文通过详细分析，提出了一种FPGA伺服控制器方案，并通过试验，验证了可行性。由于该方案完全基于硬件设计，具有更高的可靠性，同时也缩短了重构周期，具有一定的实用价值。

[1]袁鹏程,张伟峰.改进的M/T法在电机测速中的应用[J].轻工机械,2012,30(1)： 59-62.

[2]陈建国,黄河.PID数字控制器多指标优化模拟设计方法研究[J].计算机测量与控制,2012,20(6)： 1530-1534.

[3]姚战江,袁景淇,姚毅.基于FPGA的多路伺服电机的智能控制[J].农产品加工(学刊),2008(3)： 85-87.

[4]朱丽萍,何志伟,黄少先.FPGA的结构原理及在交流伺服电机中的应用[J].电机电器技术,2004(1)： 31-33.

[5]林立.无速度传感器永磁同步主轴电机伺服控制器的FPGA实现[J].微电机,2011,44(4)： 32-37.

[6]李兵强,林辉.面装式永磁同步电机电流矢量直接控制技术[J].中国电机工程学报,2011,31(S1)： 288-294.

[7]王庆龙,张崇巍,张兴.交流电机无速度传感器矢量控制系统变结构模型参考自适应转速辨识[J].中国电机工程学报,2007,27(15)： 70-74.

[8]王红,彭亮,于宗光.FPGA现状与发展趋势[J].电子与封装,2007,7(7)： 32-37.

[9]易龙强,戴瑜兴.SVPWM技术在单相逆变电源中的应用[J].电工技术学报,2007,22(9)： 112-117.

[10]耿丹.Cordic算法研究与实现[J].遥测遥控,2007,28(S1)： 39- 42.

[11]郑立岗,吕幼新,向敬成,等.一种基于Cordic算法的数字鉴频方法[J].信号处理,2003,19(1)： 6-10.

[12]周卫平,吴正国,唐劲松,等.SVPWM的等效算法及SVPWM与SPWM的本质联系[J].中国电机工程学报,2006,26(2)： 133-137.

[13]徐国库,陈禾.基于Cordic算法的坐标转换电路的FPGA实现[J].现代电子技术,2006,29(10)： 108-110.

[14]杨海钢,孙嘉斌,王慰.FPGA器件设计技术发展综述[J].电子与信息学报,2010,32(3)： 714-727.

[15]万书芹,陈宛峰,黄嵩人,等.基于改进CORDIC算法实现高速直接数字频率合成器[J].仪器仪表学报,2010,31(11)： 2586-2591.

[16]周长攀,苏健勇,杨贵杰,等.基于双零序电压注入PWM策略的双三相永磁同步电机矢量控制[J].中国电机工程学报,2015,35(10)： 2522-2533.

Permanent Magnet Synchronous Motor Servor System Based on Field Programmable Gate Array*

XINGTianyu,WANGXiaohong,TIANLianfang

(College of Automation Science and Engineering,South China University of Technology, Guangzhou 510640, China)

A permanent magnet synchronous motor servo control system was presented based on FPGA(EP4CE30F23C8) produced by Altera company, to discuss the corresponding vector conversion, coordinate transformation and other policies such as SVPWM， Cordic and PID control， and FPGA-based controller to achieve, given the overall system structure based on PWM converter, some experiments were given and the experiment results showed the good performance of the system.

field programmable gate array(FPGA); vector control; permanent magnet synchronous motor(PMSM)； servor system

广州市重大产学研专项(201508030040);广东省省级科技计划项目(2015A010106004);广东省科技厅其他科技计划项目(2013B011301012)

邢天宇(1992—)，男，硕士研究生，研究方向为运动控制及嵌入式系统开发。

王孝洪(1976—)，男，副教授，硕士生导师，从事电力电子技术及其应用方面的研究。

TM 351

A

1673-6540(2016)08- 0026- 05

2016-02-29

田联房(1968—)，男，教授，博士生导师，从事自动控制应用方面的研究。