一种拟随机初始化模拟退火粒子群算法

王　杰，　李慧慧，　彭金柱

(郑州大学 电气工程学院　河南 郑州 450001)



一种拟随机初始化模拟退火粒子群算法

王杰，李慧慧，彭金柱

(郑州大学 电气工程学院河南 郑州 450001)

针对粒子群优化算法在求解高维问题时易出现的早熟收敛、停滞现象，提出一种拟随机初始化模拟退火粒子群算法.采用Hammersley方法对算法进行初始化，可以提高算法在高维搜索空间的搜索能力，进一步将模拟退火思想引入到粒子群优化算法中，结合粒子群优化算法的快速寻优能力和模拟退火算法的概率突跳特性，使算法具有跳出局部最优从而实现全局最优的能力.分别在5个经典测试函数上测试算法的性能，仿真实验结果表明，提出的算法有效克服了传统粒子群优化算法在求解高维空间优化问题时易出现的停滞现象，在进化后期仍保持较强的搜索能力，提高了传统粒子群优化算法在高维空间的全局寻优能力.

拟随机序列； 初始化； 模拟退火； 粒子群优化

0　引言

粒子群优化(particleswarmoptimization,PSO)算法是一种基于群体智能的全局随机搜索算法[1]，有很好的生物社会背景，对许多优化问题都表现出较强的寻优性能，在科学研究中得到了广泛关注[2-4].为增加种群多样性，提高PSO算法局部探索能力，文献[5]将高斯变异引入到PSO中，文献[6]则使用了变异、选择和繁殖多种操作，同时自适应确定速度更新公式中的邻域最佳位置以及惯性权值和加速常数.其中，基于算法融合的模拟退火PSO算法充分利用了PSO算法的快速收敛能力和模拟退火(simulatedannealing,SA)算法局部极值突跳特性的优点，改善了传统PSO算法易出现早熟收敛和陷入局部极值的缺点[7-9].文献[9]将SA算法与PSO算法结合，利用SA算法的全局搜索能力，改善了PSO算法易陷入局部最优的不足.但在求解高维空间优化问题时，PSO中粒子会向自身历史最佳位置或群体历史最佳位置聚集，形成粒子种群快速趋同效应，容易出现局部极值、早熟收敛和停滞现象.为此，文献[10]提出了协作PSO算法，利用多个独立种群在目标搜索空间中的不同维度上分别进行搜索，每一个优化解由多个独立种群协作完成，每个群体只负责优化这个解向量某些维上的分量.文献[11]提出了一种既可以进行D维空间搜索，又能在不同维上选择不同学习对象的新的学习策略CLPSO.CLPSO的每个粒子都随机地向自身或非自身粒子的历史最优学习，并且其每一维可以向不同的粒子学习，该学习策略改善了PSO算法求解多峰值问题的性能，但算法学习过程较为复杂.

均匀分布随机数进行初始化容易实现，但对高维空间问题进行初始化时，易出现粒子向边缘聚集现象，采用Hammersley方法进行初始化的PSO算法改善了标准粒子群易早熟收敛的缺点，然而算法在求解高维多峰值问题时优化精度较差，易陷入局部最小，算法进化后期会出现停滞现象，精度仍需进一步提高.本文提出一种拟随机初始化模拟退火粒子群算法，从种群初始化与搜索策略两个方面对传统PSO进行改进.将改进算法(H-SA-PSO)与标准PSO算法及Hammersley初始化的PSO算法(H-PSO)进行对比分析，分别在5个通用测试函数上进行了仿真计算，验证了算法的有效性.

1　粒子群优化(PSO)算法

在PSO算法中，将多维搜索空间中优化问题的解看作一个没有质量和体积的粒子，每个粒子以一定的速度在解空间运动，每个粒子根据其自身最优和群体最优粒子位置调整速度.假设在一个D维的目标搜索空间中有n个粒子组成一个群落,其中第i个粒子表示为一个D维向量xi=(xi1, xi2,… ,xiD),i=1,2,…,n, 即第i个粒子在D维搜索空间中的位置为xi,每个粒子的位置代表一个潜在的解.将xi代入一个目标函数就可以计算其适应度值, 根据适应度值的大小衡量xi的优劣.第i个粒子的速度也是一个D维向量, 记为vi=(vi1, vi2,… ,viD),i=1,2,…,n，记第i个粒子最终搜索到的最优位置为pi= (pi1,pi2,… ,piD),i=1,2,…,n，整个粒子群最终搜索到的最优位置为pg=(xg1,xg2，…,xgD).在每一次迭代中，粒子更新当前速度和位置为

vid(t+1)=wvid(t)+c1r1(t)(pid(t)-xid(t))+c2r2(t)(pgd(t)-xid(t)),

(1)

xid(t+1)=xid(t)+vid(t+1),

(2)

式中：c1和c2为加速常数，分别调节粒子向自身最优位置飞行的步长与向全局最优位置飞行的步长，通常c1+ c2≤ 4；r1, r2～ U(0,1)为两个相互独立的随机函数；w为惯性常数，可以平衡全局与局部搜索能力.

2　拟随机初始化模拟退火粒子群算法

为了使粒子能够在较高维度的搜索空间中跳出局部最优收敛到全局最优点，本文提出了改进模拟退火粒子群算法，主要从种群初始化与搜索策略两个方面对基本PSO算法进行改进.Hammersley序列是一种拟随机低偏差序列[12]，采用此方法对PSO算法进行初始化，拟随机序列的低偏差性使初始种群能够均匀覆盖整个搜索空间，可以有效改善初始种群向边缘聚集的现象，从而避免算法过早收敛；同时将SA思想引入到PSO算法中，以概率接受PSO算法得到的劣解，有效地解决了标准PSO算法易陷入局部最优尤其对高维解空间寻优效果差的问题.

2.1初始化方法

Hammersley序列简单描述如下[12]：

对于任意非负整数i和素数基p，定义

(3)

式中：ak[0,p-1].

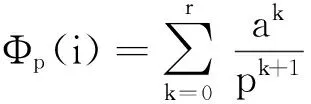
(4)

由式(3)、(4)推出Φp(i)(0,1).在D维采样空间中，设互异素数序列p1, p2,… , pD-1，定义序列Φp1,Φp2,…,ΦpD-1，则第i个Hammersley点定义为

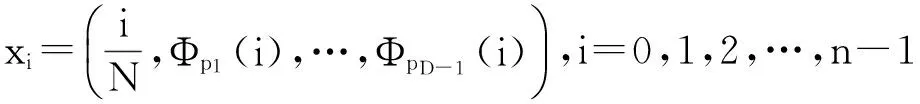
(5)

采用Hammersley法对需要搜索的D维空间进行采样，将所得到的点集作为粒子群的初始解.进而根据所得到的初始化粒子位置，采用one-rand方法对粒子速度进行初始化：

vid=(xmax,d-xmin,d)U(0,1)-xid.

(6)

2.2退火策略

2.2.1初始温度值初始温度值是影响SA算法全局搜索性能的关键参数.初始温度越高，全局搜索能力越强，搜索到全局最优解的可能性越大，但搜索时间越长；反之，虽然减少了搜索时间，但可能无法搜索到全局最优解.采用基于适应度和接受概率的温度初始化方法，初始温度T0为

(7)

2.2.2退火速度每一次外循环结束后进行降温，再进行下一次的内循环过程.这里采取较简单的温度线性下降策略:

T(t+1)=λT(t),0<λ<1 ,

(8)

退火速度足够慢有利于全局搜索，按温度衰变实施降温过程，一般λ为大于0接近于1的常数.

2.3参数设置

式(1)所示的粒子速度是一个随机变量，则由式(2)产生的粒子运动轨迹是不可控的，使得粒子在搜索空间随机跳动.为此，一般有vid∈[-vmax,vmax].vmax增大，有利于全局搜索；vmax减小，则有利于局部搜索.合理选择vmax的大小，有利于算法更好地收敛到全局最优值.

vmax=αvmax,0<α<1.

(9)

采用衰变因子法动态调整vmax，有利于算法在整个搜索过程保持较好的优化性能.

2.4算法步骤

采用Hammersley方法对种群粒子初始位置进行初始化，根据所得到的粒子位置采用one-rand方法对粒子速度进行初始化，能够使得初始种群尽可能覆盖整个搜索空间，从而提高了PSO算法的全局搜索能力.为进一步改善算法的全局搜索能力，使算法可以达到更好的收敛精度,将SA算法的概率突跳特性引入到PSO，有助于PSO算法跳出局部最优.即对PSO算法中每一代产生的新的粒子，按照SA算法中的概率接受准则更新粒子位置.具体算法步骤如下：

1) 初始化：给定算法种群规模、变量维数、学习因子、惯性权重、初始温度、最大迭代次数.进化迭代次数t=1，采用Hammersley方法对需要搜索的维空间进行采样，将所得到的点集作为粒子群的初始解.进而由式(6)对粒子速度进行初始化.

2) 评价初始种群，确定局部及最优粒子位置.

3) 由式(1)、(2)更新当前粒子速度与位置.

4) 判断当前迭代次数是否达到设定的最大迭代次数？是，直接跳至步骤9)；否，则继续执行.

5) 计算所有粒子适应度，更新局部及全局最优粒子位置.

6) 由式(1)、(2)更新当前粒子速度与位置.

7) 所有当前粒子位置xi(t)和新的粒子位置xi(t+1)，根据目标函数分别计算所对应的f(xi(t))和f(xi(t+1))，并计算增量f=f(xi(t+1)) - f (xi(t)).

9) T=λT,vmax= α vmax,t = t+1,跳至步骤4)，继续执行.

10) 输出当前最优粒子位置为最优解，算法终止.

3　仿真计算

3.1测试函数

为测试算法的性能，选取5个通用的标准测试函数[9]在不同维度下进行仿真计算：

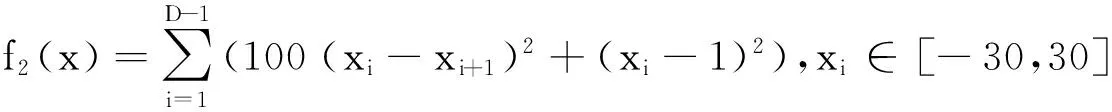
以上5个标准测试函数的形态各异，能够全方位测试算法的性能.f1与f2为连续单峰函数，通常用于衡量算法的收敛速度.函数f3f5是复杂的非线性多峰函数，存在大量的局部极值，通常用于衡量算法的种群多样性及全局搜索性能.

3.2实验结果及分析

分别采用H-PSO算法与H-SA-PSO算法对文献[9]中给出的5个测试函数进行仿真计算，主要参数设置与文献[9]一致,其中：粒子群规模(小于30维)为30，粒子群规模(大于30维)为50，惯性权重w=0.729，c1=c2=1.494 45，最大迭代次数为1 000，初始温度为T0，温度下降系数λ=0.995.此外，文献[9]中当适值小于10-10时输出0，本文算法记录为0的实验结果均小于10-16.对5个测试函数在不同维度下进行了实验，50次运算的最优适值平均值的计算结果与文献[9](PSO算法)的计算结果如表1所示.50次实验结果的平均种群最优值进化曲线如图1～5所示.

所有相关算法都运行在戴尔vostro1088双核2.0GHz的CPU的MatlabR2010b的环境下.

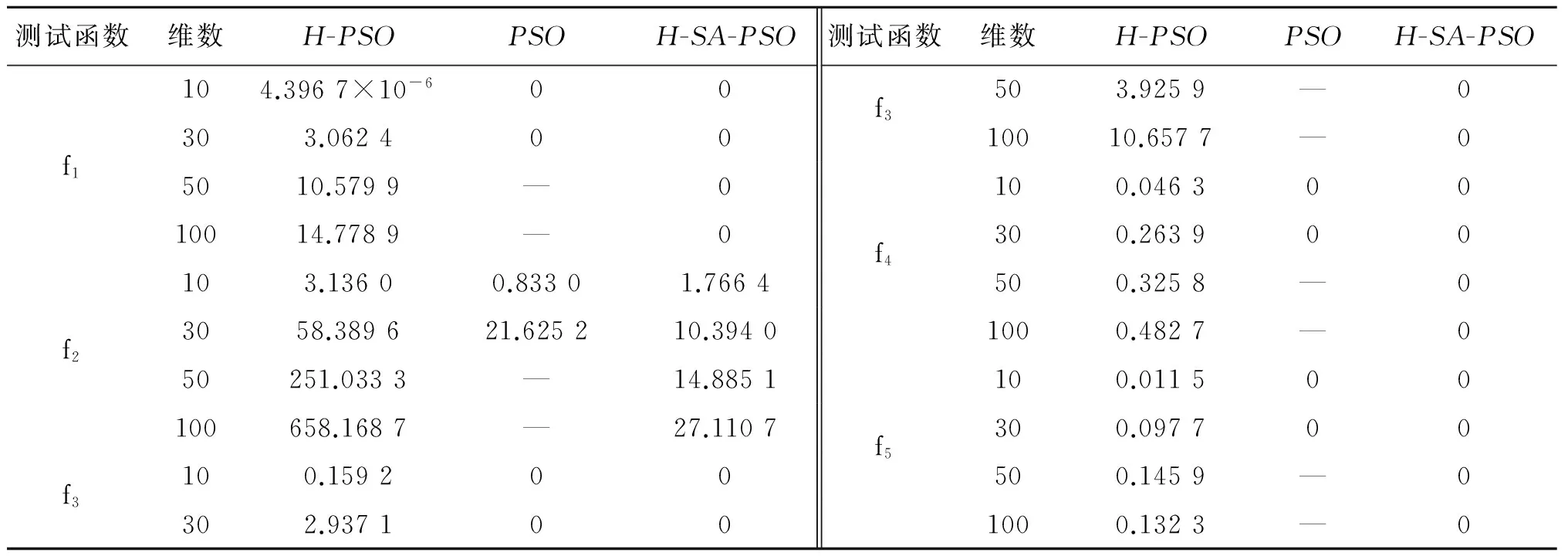
表1　三种算法的仿真结果Tab.1　The simulating results of the three algorithms

对比表1结果可以看出，H-SA-PSO算法测试结果明显好于H-PSO算法.对除f2以外的其余4个测试函数，相比文献[9]中结果，在更高维的搜索空间，可以在规定的迭代步数内成功寻得函数最优值，有更强的全局寻优能力.f2是复杂单峰值函数，虽然没有在规定的迭代次数内对其寻优成功，但是相比于文献[9]中结果，可以达到更好的精度，尤其对高维(大于30维)情况下的寻优，优势更加明显.因此，H-SA-PSO算法在解决高维复杂函数时有较好的寻优能力.

图1　函数f1寻优过程Fig.1　The optimization process of f1

图2　函数f2寻优过程Fig.2　The optimization process of f2

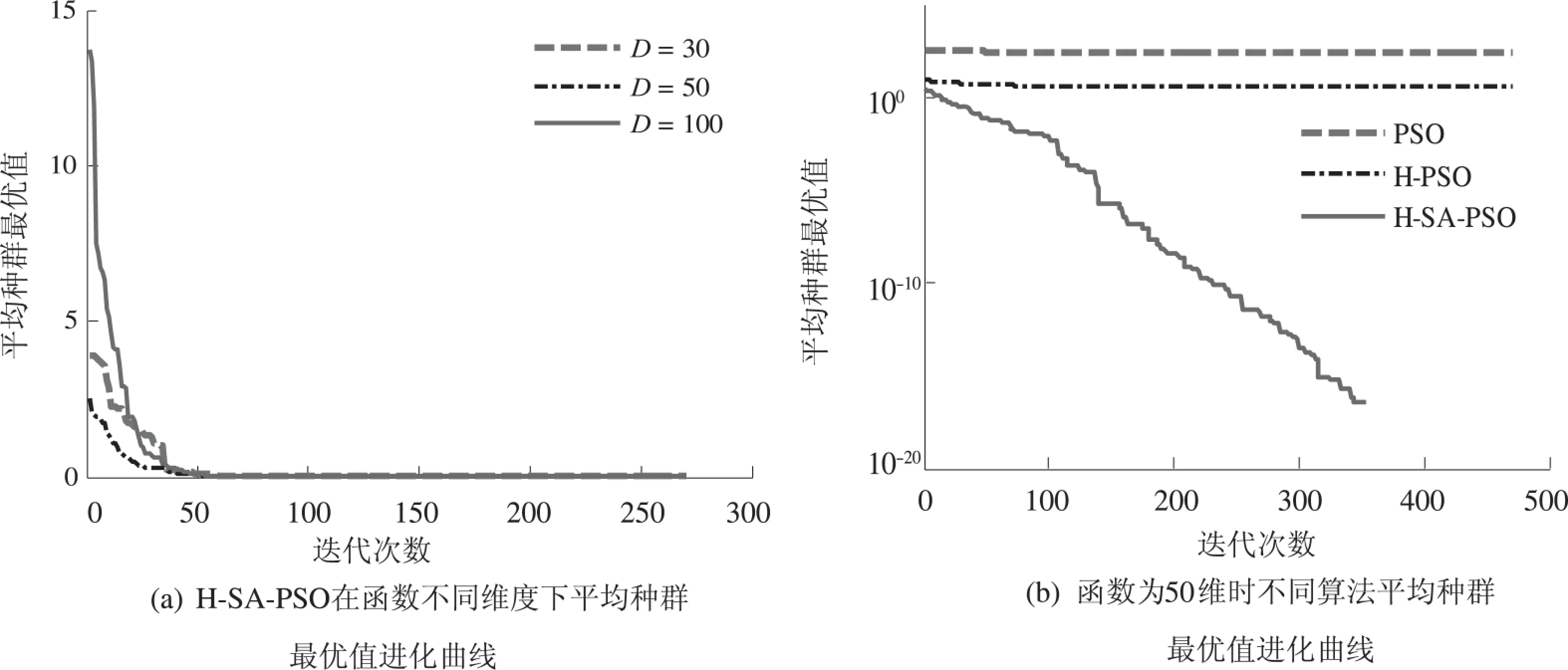
图3　函数f3寻优过程Fig.3　The optimization process of f3

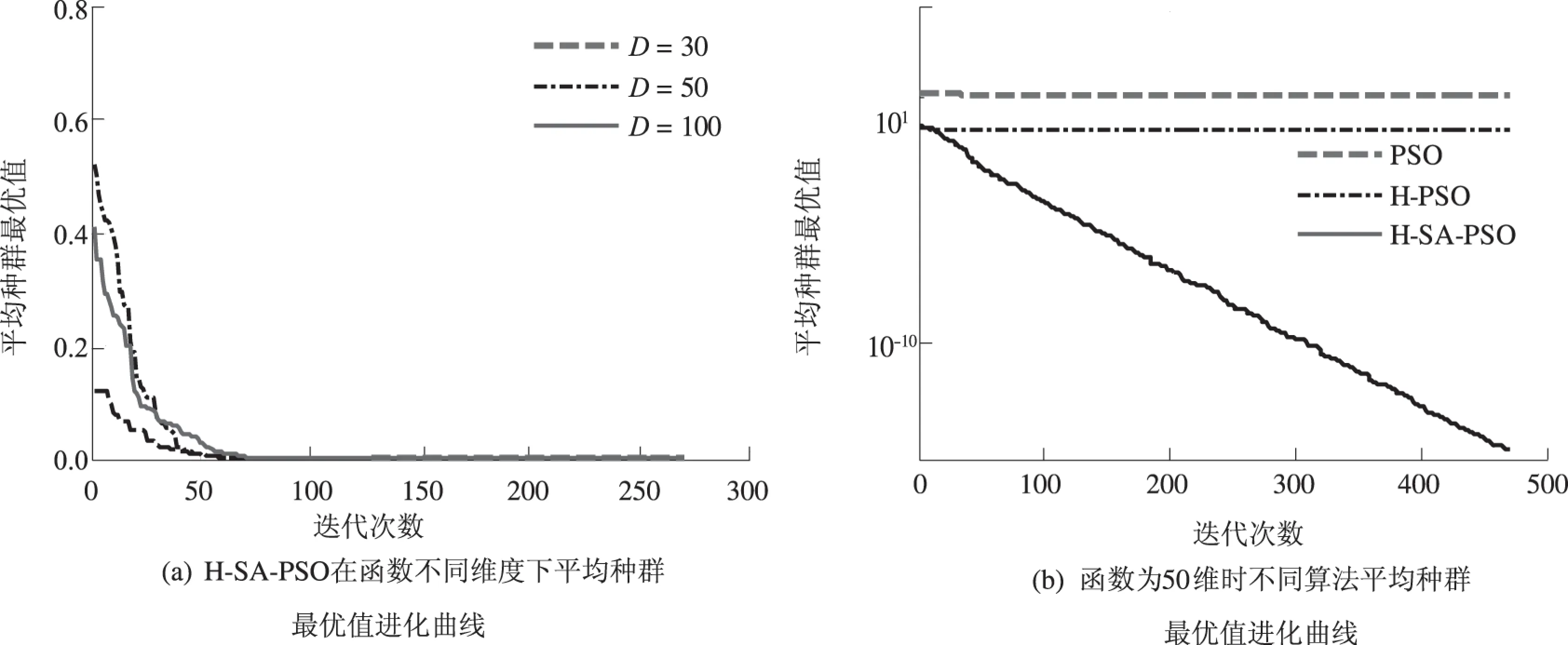
图4　函数f4寻优过程Fig.4　The optimization process of f4

从图1～5可以看出，H-PSO算法相比于标准PSO优化算法可以得到更好的初始解，从而达到更好的收敛精度，算法性能有所提高，但是容易陷入局部极值.H-SA-PSO算法有更好的初始种群，且不易陷入局部最优，对高维度的测试函数在较少的迭代次数内找到全局最优值，有效克服了停滞现象，在进化后期依然保持较好的寻优性能，具有很强的局部及全局搜索能力，有效解决了传统粒子群在求解高维复杂问题时寻优效果不佳的问题.

图5　函数f5寻优过程Fig.5　The optimization process of f5

4　小结

提出了拟随机初始化模拟退火粒子群算法，运用Hammersley方法初始化粒子群，使得PSO初始种群能够均匀覆盖整个搜索空间，避免了传统初始化方法在解决高维空间优化问题时易于向边缘聚集的现象，有利于PSO算法在高维空间中的寻优.同时将SA思想引入到PSO算法中，结合了PSO算法的快速寻优能力和SA的概率突跳特性，使算法可以跳出局部最优从而实现全局最优，达到更好的收敛精度.仿真计算结果表明，本文算法在求解高维复杂函数时优势明显，算法在进化后期仍有较强的搜索能力，有效改善了传统PSO算法在求解高维问题时容易出现的停滞现象，不易陷入局部极值且收敛精度较高，是一种有效求解高维函数的全局优化算法.

[1]GARNIERS,GAUTRAISJ,THERAULAZG.Thebiologicalprinciplesofswarmintelligence[J].Swarmintelligence, 2007,1(1):3-31.

[2]刘逸. 粒子群优化算法的改进及应用研究[D].西安:西安电子科技大学,2013.

[3]FENGMY,PANH.AmodifiedPSOalgorithmbasedoncachereplacementalgorithm[C]//TenthInternationalConferenceonComputationalIntelligenceandSecurity.Kunming, 2014:558-562.

[4]LANGDONWB,POLIR.Evolvingproblemstolearnaboutparticleswarmandotheroptimisers[C]//IEEECongressonEvolutionaryComputation.Edinburgh,2005:561-578.

[5]HIGASHIN,IBAH.ParticleswarmoptimizationwithGaussianmutation[C]//ProceedingsoftheIEEESwarmIntelligenceSymposium.Indianapolis, 2003: 72-79.

[6]MIRANDAV,FONSECAN.EPSO:evolutionaryparticleswarmoptimization,anewalgorithmwithapplicationsinpowersystems[C]//TransmissionandDistributionConferenceandExhibition.Yokohama, 2002:2491-2505.

[7]刘爱军,杨育,李斐,等.混沌模拟退火粒子群优化算法研究及应用[J].浙江大学学报(工学版),2013,47(10):1722-1730.

[8]YANGHF,YANGZY,YANGY,etal.Animprovedparticleswarmoptimizationalgorithmbasedonsimulatedannealing[C]// 10thInternationalConferenceonNaturalComputation.Xiamen, 2014: 529-533.

[9]吕丹,童创明,钟卫军. 基于粒子群和模拟退火算法的混合算法研究[J]. 计算机工程与设计，2011, 32(2):663-666.

[10]BERGHF,ENGELBRECHTAP.Acooperativeapproachtoparticleswarmoptimization[J].IEEEtransactiononevolutionarycomputation, 2004,8(3): 225-239.

[11]LIANGJJ,QINAK,SUGANTHANPN,etal.Comprehensivelearningparticleswarmoptimizerforglobaloptimizationofmultimodalfunctions[J].IEEEtransactiononevolutionarycomputation, 2006, 10(3): 281-295.

[12]HARALDNE,SIANGJINGYA.Halton-typesequencesfromglobalfunctionfields[J].ScienceChinamathematics, 2013,56(7):1467-1476.

(责任编辑：孔薇)

AQuasi-randomizedInitializedSimulatedAnnealingParticleSwarmOptimizationAlgorithm

WANGJie,LIHuihui,PENGJinzhu

(School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China)

Toovercometheshortcomingsofparticleswarmoptimization(PSO)algorithmsuchasprematureconvergenceandstagnationwhensolvingthehigh-dimensionalproblems,aquasi-randomizedsimulatedannealing(SA)-PSOalgorithmwasproposed.Theperformanceofalgorithminhigh-dimensionaloptimizationspacecouldbeimprovedbyusingtheHammersleyinitialization.AndtheideaofSAalgorithmwasintroducedintothePSOalgorithm,combiningwiththefastsearchingabilityofPSOandtheprobabilisticjumpingpropertyofSA,tojumpoutoflocaloptimalalgorithmtoachievetheglobaloptimum.Theproposedalgorithmcouldeffectivelyovercomethestagnationphenomenon,enhancetheglobalsearchabilityinhigh-dimensionalspace.Theproposedalgorithmwasthentestedon5differentfunctions,andtheresultsdemonstratedbetteroptimizationabilityoverthetraditionalPSOalgorithm.

quasi-randomsequence;initialization;simulatedannealing;particleswarmoptimization

2016-02-01

教育部高等学校博士学科点专项科研基金资助项目(20124101120001)；河南省教育厅科学技术研究重点项目(14A413009)；中国博士后科学基金资助项目(2014T70685)．

王杰(1959—)，男，河南周口人，教授，主要从事模式识别与优化算法研究,E-mail:wj@zzu.edu.cn.

TP301

A

1671-6841(2016)03-0075-07

10.13705/j.issn.1671-6841.2016022

引用本文：王杰，李慧慧，彭金柱.一种拟随机初始化模拟退火粒子群算法[J].郑州大学学报(理学版)，2016，48(3)：75-81.