基于AP法的无背索斜拉桥强健性分析

邓海斌，　陈　文，　王晓明

(1.湖州市公路管理局,浙江 湖州，313000；2.西北水利水电工程有限责任公司,陕西 西安　410008；3.长安大学 桥梁所,陕西 西安　710064)



基于AP法的无背索斜拉桥强健性分析

邓海斌1，陈文2，王晓明3

(1.湖州市公路管理局,浙江 湖州，313000；2.西北水利水电工程有限责任公司,陕西 西安410008；3.长安大学 桥梁所,陕西 西安710064)

针对无背索斜拉桥的自平衡特征，分别以主梁最小变形安全系数和最大应力安全系数作为结构性能参数，对不同位置拉索断裂的损伤场景进行易损性分析，获得此类桥型的强健性基本特征。运用构件极值空间分布特性的后处理技术对桥梁的响应规律做了相应的探索，并对静动力计算的差别做了详细的比较。提出基于破坏结果的改变传力路径法的结构强健性分析方法。以某无背索斜拉桥为例，采用提出的方法，选出造成后果尽可能严重而占自身结构比例尽量低的场景。分析结果得出结构的不同拉索位置的断裂敏感性，并可为桥梁健康监测中监测内容的选取及传感器布设提供参考。

无背索斜拉桥；强健性；无损分析；AP法；静损分析；动损分析

0　引言

结构的强健性(robustness)[1-3]反映了结构整体抵抗意外事件的能力，区别于传统构件层次，属于结构体系层次的安全分析范畴。整体性很好的结构，在意外事件发生时和发生后能够保持整体稳定性，不会发生与其原因不相称的倒塌或连续破坏，则可称结构的强健性大，相应的易损性(vulnerability)[4]小。英国的结构安全标准委员会(SCOSS)把结构的强健性、增加结构的安全储备、加强对设计和施工过程的安全监督检查规定为确保结构安全不可忽视的3个重要措施[4]。特别是9.11事件后，强健性成为继“安全性、适用性、耐久性”以外另一个重要的结构性能评价指标。

无背索斜拉桥通过倾斜桥塔的自重力矩来实现对主梁的提升作用，其体系的自平衡特性强。斜拉索断裂后塔、梁的原有平衡都会被打破，强健性分析更重要。

拉索强健性的研究起步较晚，但国内外的研究方法及手段发展的已经较成熟，且研究均是在偶然荷载的作用下完成的，但对其他意外事故研究不多，成果没有系统性[2]。本文将以无背索斜拉桥为背景展开拉索断裂的体系强健性研究，分析得出的不同工况下的体系强健性可为全桥运营和加固提供指导。

1　无背索斜拉桥的强健性评价方法

1.1体系冗余度指标

无背索斜拉桥的强健性与体系的冗余度有着密切的关系。当意外事件造成体系原有平衡状态破坏后，结构通过内力重分配，启用备用传力路径，保持结构不至于发生整体破坏，甚至仍能继续部分承载。因此，结构的冗余度越高，则传力路径越多，强健性也越强。冗余度可定义为

(1)

式中,Lint act为初始结构破坏荷载系数；Ldamage为结构受损后的破坏荷载系数。

本文的体系破坏准则定义为需同时考虑强度η和变形μ，即当结构受力或变形任一项超过阈值时，则认为结构破坏。因此，体系的冗余度指标为

(2)

式中,η、η*分别为初始和受损结构的强度；μ、μ*分别为初始和受损结构的变形破坏荷载系数。

需要指出的是，无背索斜拉桥拉索的不同则对应的冗余度指标不同。本文将关键拉索所对应的R定义为体系的冗余度指标。

1.2敏感性指标与关键构件的识别

结构中不同的构件对结构整体承载力性能的影响程度是不同的。因此，采用敏感性指标S.I.进行构件的损伤对结构承载力的影响的评价，进而可选出结构中的关键构件，为后续的动力分析做准备。

敏感性指标的定义为构件失效后结构的剩余承载能力λ0-λdamage与其初始承载能力λ的比值。

(3)

2　基于破坏结果的改变传力路径法(AP法)

根据侧重点的不同，可将拉索损伤动力分析分为两大类方法：考虑破坏原因的结构动力分析法以及基于破坏结果的改变传力路径法(Alternate path，简称为AP 法)[5]。

考虑破坏原因的结构动力学分析法，指的是分析结构动力响应时考虑引起该响应的原因，如车桥碰撞分析中车辆模型的建立[6-7]，船桥碰撞分析中船舶模型的建立[8-9]等。该方法可较完整的分析出结构在特定荷载下的连续倒塌及塑性发展规律，但分析时需建立破坏源模型并选取合理的破坏模式，这对研究人员的跨学科知识储备要求较高，而且基于破坏原因的结构动力学分析工作量较大，计算效率低下。

改变传力路径法在建筑文献中也称“抽柱法”[10]或者“构件拆除法”[11]，但核心思想是一致的：即只需考虑某些构件退出工作后剩余结构的响应而不考虑引起结构破坏的原因。此方法只需对剩余结构进行动力学行为的模拟分析，无需建立破坏源模型，计算时，工作量较前种方法小，可操作性强，计算效率高。因此该方法在工程结构的强健性设计与分析中得到了较为广泛的应用。

2.1AP法基本方程

完好结构在车辆荷载P作用下的动力平衡方程为

(4)

若拉索i发生破坏，其对结构的作用力也将随破坏的发生逐渐消失。如图1所示，将该拉索索力用等效节点力Fi(t)代替，则断索过程的动力平衡方程变为

(5)

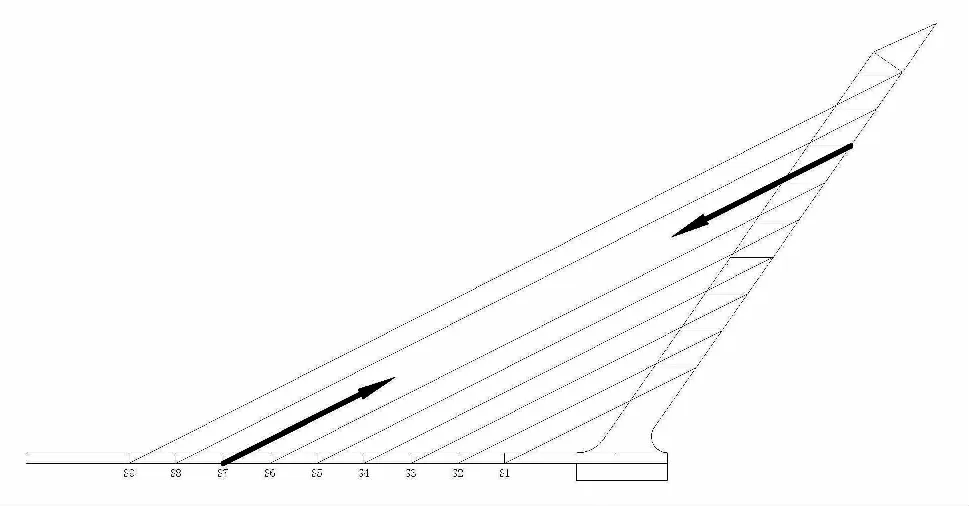
图1　AP法Fi(t)力的加载模式示意图

图2　摆线式加载力的示意图

为了准确模拟整个断索过程中的结构效应，本文采用了瞬态动力分析法，Fi(t)的加载模式采用摆线模式，如图2所示，该模式可较好的模拟断索前的静态稳定、断索过程中的瞬间响应以及断索后的效应。具体如下

(6)

式中，Fi为退出工作的构件在无损模型中的内力值；τ为作用上升时间。结合文献[12]，对力的作用上升时间做如下规定：τ/T≥2，其中T为基本周期。

在模拟拉索断裂的分析中，时间步长的大小对分析结果有显著影响，根据文献[12]，构件失效时间应小于荷载数据的时间间隔和0.1倍损伤后结构相关模态周期，故本文采用基本振型周期的1/10。

2.2结构阻尼

斜拉索断裂后，剩余结构的固有频率和固有振型，是确定AP法分析所需的结构阻尼的参数。

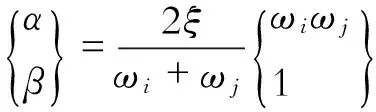
根据文献[12]，本文ωi取剩余结构的基频，ωj根据对动力反应有明显作用的高阶振型而确定。综合而看，采用ξ=0.02 的阻尼比作为计算基础数据。

3　算例分析

某无背索斜拉桥，主塔和主梁均采用C55混凝土，计算容重为24 kN/m3，铺装层容重取21.2 kN/m，双侧护栏为13.7 kN/m，设计荷载取公路-Ⅱ级。全桥拉索共8对，编号从塔根到塔顶处为S1～S8。

3.1体系强健性评价与关键拉索识别

3.1.1无损结构的分析

无损结构加载时，恒载采用结构自重，活载采用公路Ⅱ级加载，荷载系数L为公路Ⅱ级荷载的倍数。

(7)

图3　不同荷载系数下最大索力

图4　不同荷载系数下主梁挠度

如图3所示，当荷载系数值达22.7时拉索S3最先破坏，此时拉索失效，随荷载系数的增大，S3附近的拉索应力迅速增加，拉索连锁断裂的情况发生。由规范得，在汽车荷载(不计冲击力)的作用下，混凝土主梁最大竖向容许挠度为L/500。而荷载系数为3时，如图4所示，主梁挠度值已达容许值，但此时结构仍可继续承载；直至λ=22.7时，拉索S3失效，此时判定为结构的极限状态，因此极限荷载系数22.7。

3.1.2单根拉索AP分析体系的强健性分析

S1的上游侧拉索表示为S1-1，下游侧表示为S1-2，其余编号如同上述。S5为跨中拉索，S1为靠近塔顶处拉索。定义单侧单根拉索断裂工况如下：跨中处拉索断裂为S5-1，四分点处拉索断裂为S2-1、S8-1，如图5～图8所示。

将上述计算结果列出如表1所示。

图5　不同荷载系数下最大索力、最大主梁挠度图

图6　S2-1拉索断裂情况下剩余索力图

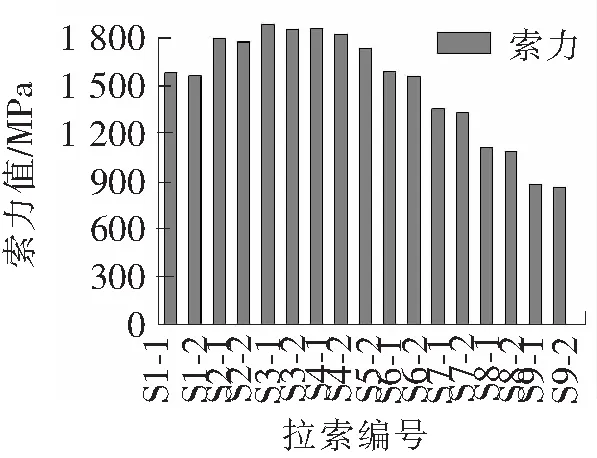
图7　S5-1拉索断裂情况下剩余索力图

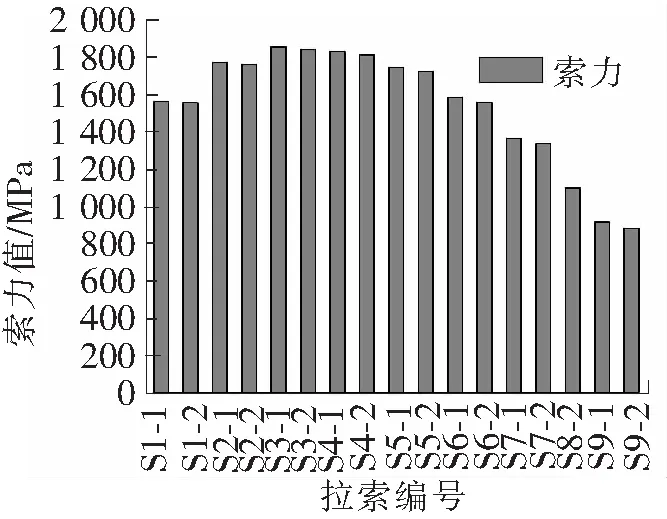
图8　S8-1拉索断裂情况下剩余索力图

拉索编号荷载系数敏感性指标结构冗余度S2-1220.030832.4S5-121.50.05318.9S8-122.50.009113.5

从上述单侧不同位置的单索分析中可得，拉索S5-1的断裂对结构承载能力影响最大即结构敏感性最大，而拉索S8-1的断裂对结构承载能力影响最小即结构的敏感性最小，因此可认为S5-1为关键拉索。

极限荷载的作用下，3种工况均为拉索S3-1率先断裂，且从剩余索力值也可得出，S3-1附近的索力明显大于其他位置。因此，在极限荷载下中间的拉索发挥了主要作用，故拉索S5附近区域为关键区域。

3.2有损结构的动力分析

3.2.1单侧多根拉索断裂体系的强健性分析

基于上述结论，则以拉索S5为中间拉索进行单侧拉索的断裂动力分析，确定TS5_3、TS5_5、TS5_7、TS5_9为4个典型工况，TS5_3表示单侧以S5拉索为中心的3根拉索断裂的工况。

采用本文所述的AP法对上述3种工况进行动损分析，如图9～图12所示，同时与对应的静损分析作对比可得：

(1)拉索失效后，剩余拉索应力在动损模型中的增幅是大于静损模型的。

(2)由表2知，失效拉索数量的增加使得主梁和桥塔的应力也增加。与静损模型相比，动损模型中应力较大，但各工况的最大压应力均在允许范围内。由强度准则知，此时结构构件尚未达极限抗拉强度。

(3)随单侧失效拉索数量的增加，主梁和桥塔的位移也在增加。当单侧拉索失效数量升至5根时，主梁的最大位移增至19 cm，且此时主梁的最大位移量已经大于规范的允许值。

(4)本分析是针对单侧拉索进行的断裂强健性分析，即桥梁在单侧拉索的断裂下不会出现结构性破坏垮塌，只是在拉索断裂数超过4根时，桥梁会因挠度过大而不宜运营。

其他工况分析结果如表3，表4。

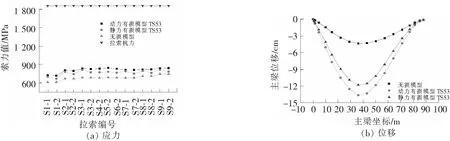
图9　TS5_3动损与无损模型索力、主梁挠度图

图10　TS5_5动损与无损模型索力、主梁挠度图

图11　TS5_7动损与无损模型索力、主梁挠度图

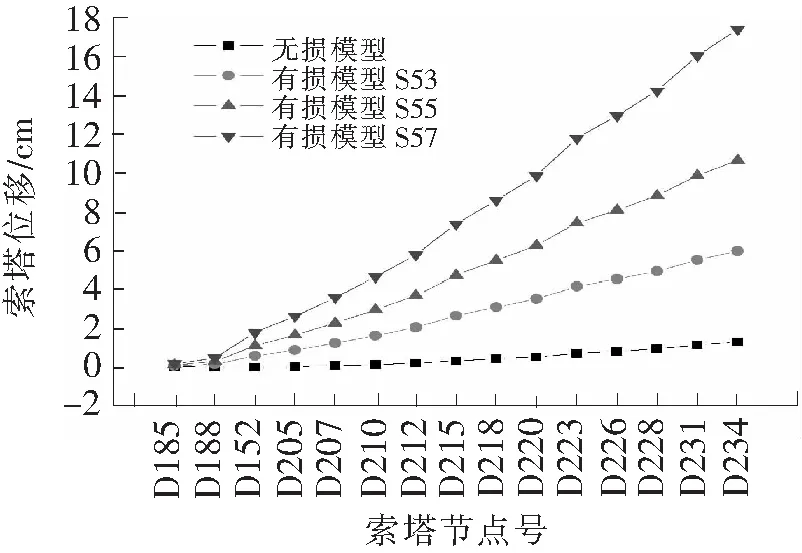
图12　不同工况下桥塔线性的影响

工况主梁应力最大值/MPa主塔应力最大值/MPa主梁应力最大位置主塔应力最大位置TS5_3-15.8-16.3桥塔根部桥塔根部TS5_5-18.6-20.1桥塔根部桥塔根部TS5_7-21.5-24.2桥塔根部桥塔根部TS5_9-23.2-27.8桥塔根部桥塔根部

表3　各工况主梁动挠度放大系数极值

表4　各工况主梁动应力放大系数极值

3.3.2双侧多根拉索断裂体系的强健性分析

选取以拉索S5为中心展开断索分析，取双侧拉索对称断裂，选择5个典型工况，分别为YS5_2、YS5_4、YS5_6、YS5_10、YS5_12。其中前3种工况如图13～图15所示。

从表5可知，在YS5_12工况下，靠近桥塔根部的主梁，其压应力已超过材料抗压强度标准值，达-35.6 MPa，认为结构破坏，并且根据分析，可以得出以下结论：

(1)拉索失效后，剩余拉索应力在动损模型中的增幅是大于静损模型的，且不同工况中应力增幅亦不同，主要为随断索数的增加，剩余拉索的应力增幅也随之增大，且失效区附近的拉索最为敏感。

(2)随双侧拉索失效数量的增加，主梁和桥塔的位移也逐渐增加，当双侧拉索失效数达4根时，主梁最大位移达17.2 cm，已接近规范所规定的最大允许位移值L/500，且失效数量进一步增加时，主梁位移超过最大允许值。由变形准则得，双侧拉索的断裂不超过4根时，桥梁是安全的。

(3)由表5得，拉索失效数的增加使主梁和桥塔的应力增加，动损比静损增加多。YS5_12工况下塔梁根部应力超标，因此该桥的强健性阈值为5对索，即在双侧不超过10根索断裂的情况下是安全的。

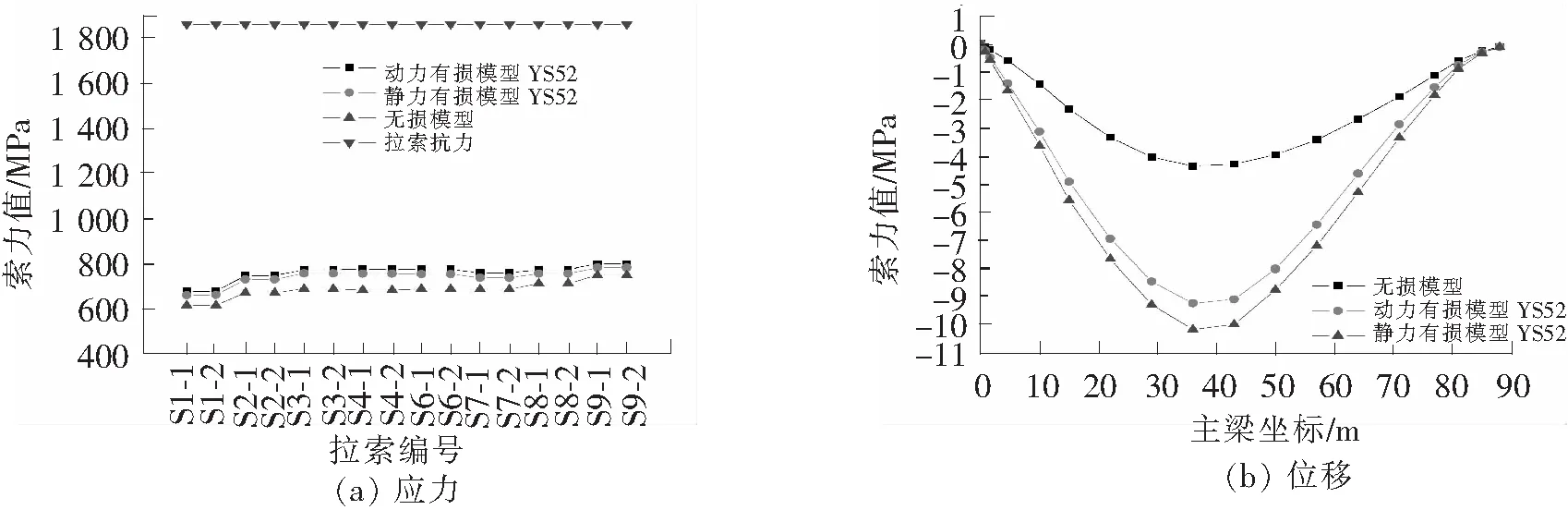
图13　YS5_2动损与无损模型索力、主梁挠度图

图14　YS5_4动损与无损模型索力、主梁挠度图

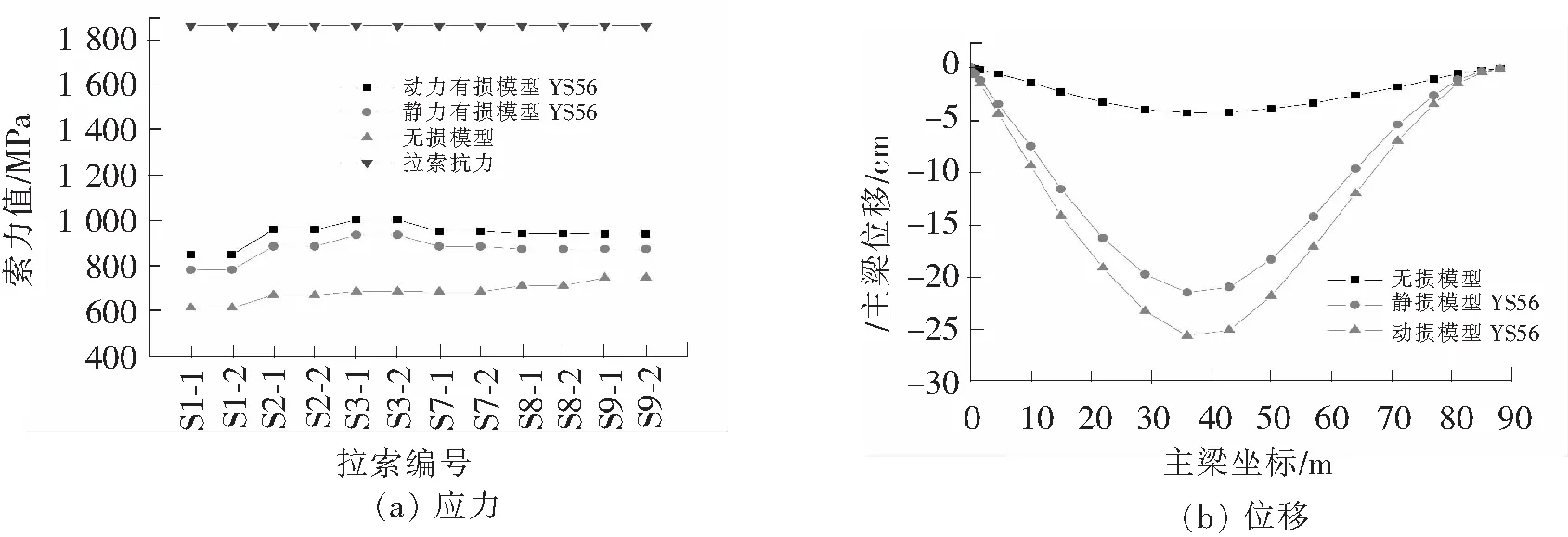
图15　YS5_6动损与无损模型索力、主梁挠度图

其他工况分析结果表示如表6，表7。

表5　各个工况下动损分析主梁和主塔最大应力值

表6　各工况主梁动挠度放大系数极值(双侧多根拉索断裂体系)

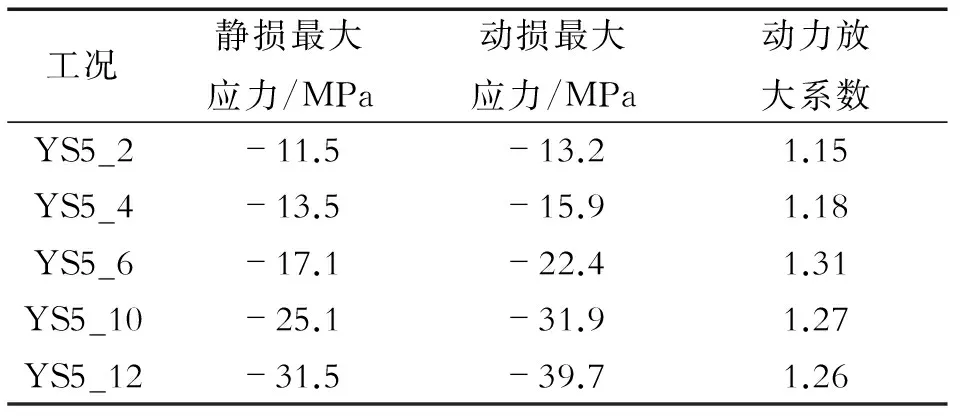
表7　各工况主梁动应力放大系数极值(双侧多根拉索断裂体系)

4　结论

(1)本文针对无背索斜塔斜拉桥的结构特点，对主要构件进行了分析，结合破坏准则研究了该桥桥强健性指标。最终确定了该桥冗余度的分析方法，以此确定出关键构件。

(2)由无损模型的敏感性分析知，确定S5附近拉索为关键区，为有损模型的分析奠定了基础。

(3)有损模型的静力分析表明，失效拉索附近区域的剩余拉索较为敏感，且应力增长高于远离桥塔拉索，无论是单侧还是双侧拉索断裂都表现出此规律。单侧拉索的断裂分析以位移准则为准，分析得强健性阈值是5根拉索。双侧拉索断裂分析准则是位移准则结合强度准则，得出强健性阈值是5根拉索。

(4)本文选用AP法进行结构动力分析，采用经典反力加载时程曲线加载。拉索失效的动力分析中桥梁力学行为的表现规律与静损分析一致。单侧拉索断裂分析以位移准则为准，分析得强健性阈值是4根拉索。双侧拉索断裂分析准则是位移准则结合强度准则，得出桥梁强健性阈值是4根拉索。

(5)相同工况下，静损和动损分析表明桥梁的力学行为基本一致，但静损分析的安全阈值高于动损分析，其本质差别产生于动力放大系数，由此动力学分析更具有意义。

(6)为保证安全运营，本文对其安全阈值建议为：桥梁任一侧的拉索断裂数量不宜超过4根。

[1]刘闯,刘西拉. 考虑结构体系冗余度的结构形式优化设计[C]//第二届全国结构工程学术会议论文集.北京：清华大学土木工程系，1993：517-522.

[2]DAN M F. Effects of Damage and Redundancy on Structural Stability[J].Journal of Structural Engineering-Asce, 1987,113(7):1533-1549.

[3]陈以一，赵宪忠. 高冗余度钢结构倒塌控制指南[M]. 上海: 同济大学出版社, 2007.

[4]张建强. 局部构件破坏对高层框架-剪力墙结构影响的研究[D].北京: 北京工业大学建筑工程学院, 2009.

[5]谢甫哲，舒赣平，凤俊敏. 基于抽柱法的钢框架连续倒塌分析[J]. 东南大学学报：自然科学版，2010(1):154-159.

[6]吴迅，王艺桥，曲兆乐. 大跨斜拉桥拉索安全性能加固方案[J]. 沈阳工业大学学报，2010(1):110-114.

[7]闫振国，邵新鹏，蔡建军，等. 青岛海湾大桥局部索构件失效对结构的影响及对策研究[J]. 上海公路，2011(4):36-39.

[8]李欣. 轨道交通无背索斜拉桥受力分析与施工监控[D].上海: 同济大学土木工程学院，2008.

[9]范立础. 桥梁工程(下)[M]. 北京：人民交通出版社，2006.

[10]王洁，武清玺. 杆系结构蒙特卡罗法计算及敏感性分析[J]. 山西建筑，2006(3): 46-47.

[11]文方针. 基于有限元概率设计的结构敏感性分析研究[J]. 华东交通大学学报，2010(1): 17-21.

[12]严爱国，刘振标，罗世东. 宜万铁路宜昌长江大桥主桥结构敏感性分析[J]. 桥梁建设，2006(S2): 83-85+89.

Research on Structural Robustness for Cable-stayed Bridge Without Back-stays

Deng Haibin1,Chen Wen2,Wang Xiaoming3

(1.Huzhou Highway Administration Bureau of Zhejiang Huzhou, Huzhou 313000, China;2.Northwest Water Conservancy and Hydropower Co., Ltd., Xi’an 710065, China;3.Institude of Bridge Eng., Chang’an University, Xi’an 710064, China)

In this paper, aiming at the self-balance feature of cable-stayed bridge without back-cable, respectively taking the safety factor of girder minimum deformation and girder maximum stress as structural performance parameters, the vulnerability of cable fracture in different damage position is analyzed, and the basic robustness feature of such bridges is obtained. Using the post-processing technology of component extremum spatial distribution feature to explore the response of bridge, a detailed comparison is made between static and dynamic calculation. A structural robustness analysis means is proposed based on alternate path method of destroy results. Taking a cable-stayed bridge without back-cable as an example, using the proposed method, the vulnerability scenarios with the most possible serious damage and lightest portion in structure is chosen. The result of the gives the sensitivity to different position of fracture structure,and can be used as a reference for choosing the monitoring content and sensors layout in structural health monitoring.

cable-stayed bridge without back-cable；robustness；nondestructive analysis；AP method；static damage analysis；dynamic damage analysis

2015-07-10责任编辑:刘宪福DOI:10.13319/j.cnki.sjztddxxbzrb.2016.03.03

国家自然科学青年基金(51308055)

邓海斌(1976-)，男，高级工程师，从事公路养护管理工作。E-mail：510041686@qq.com

U448.25

A

2095-0373(2016)03-0013-08

邓海斌，陈文，王晓明.基于AP法的无背索斜拉桥强健性分析[J].石家庄铁道大学学报:自然科学版,2016,29(3):13-20.