电热法测量热功当量实验的新探究

蔡 晨，李朝荣，李英姿，王 选

（北京航空航天大学物理科学与核能工程学院，北京 100191）

电热法测量热功当量实验的新探究

蔡 晨，李朝荣，李英姿，王 选

（北京航空航天大学物理科学与核能工程学院，北京 100191）

提出一种新的实验方案来处理电热法测量热功当量实验中装置的散热问题.采用积分法计算热功当量，求得的热功当量数值更加接近理论值，并且一元线性拟合实验数据时得到的线性关系非常强烈.

热功当量；散热系数；线性回归；相关系数

电热法测量热功当量实验的散热速率与系统和环境的温差有关，是一个变化量.目前不同版本的《大学物理实验》中对此的处理方法基本都用到了短时间内“差分代替微分近似求得散热量”的方法［1-5］，这一方法引起的误差没有量化估计，无法得知其对实验结果的准确性影响程度.另一方面，按照我校的做法得到的线性相关系数比较低，与大家惯常的认识不相符合，我们的研究正是从改善线性相关系数起步的.新方案从实验原理出发，采用积分法代替微分法，并且运用数学分析中泰勒展开的方法对公式进行近似，由此带来的误差可以计算并控制其在允许范围内，最终获得的实验结果不仅准确度高，而且具有理想的线性相关度.

1 实验原理与方案

1.1 基本原理

实验装置如图1所示.给电阻R两端加上电压V，在通电t秒时间内电场力作功W=V2t/R.系统吸收的热量为

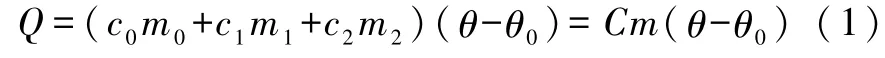
式（1）中：c0、c1、c2分别是水、量热装置及加热器的比热容；m0、m1、m2分别是其相应的质量；Cm=c0m0+c1m1+c2m2是系统的总热容；θ0为系统初温.于是可得热功当量：

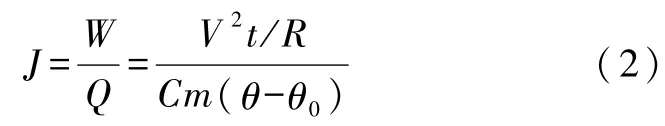
若把系统看成是理想绝热的，即只考虑系统由于通电而升温，则由式（2）对时间求导可以得到温度变化率所满足的关系式为

图1 热功当量实验装置

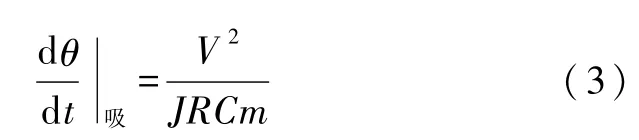
考虑到通电时系统吸热的同时也向环境中放热，根据牛顿冷却定律，由于放热引起的温度变化率为

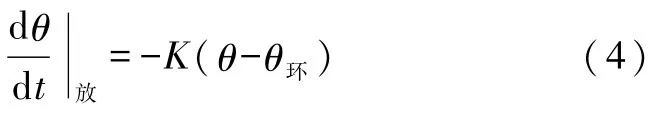
式（4）中K为系统的散热系数.综合式（3）和式（4），系统温度的实际变化率为［5］

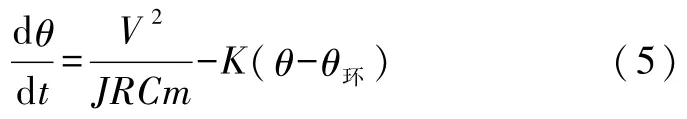
求解此一阶线性常微分方程，得

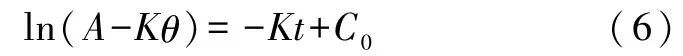
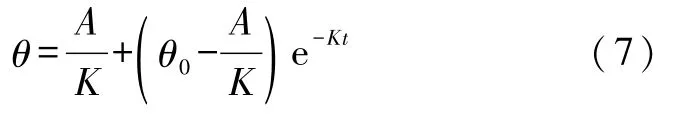
另一方面，根据牛顿冷却定律dθ/dt= -K（θ-θ环）测定散热系数K.对牛顿冷却定律积分得到

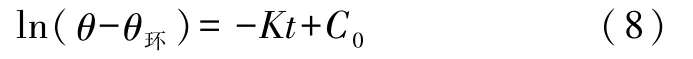
令y=ln（θ-θ环），x=t，并设y=a1+b1x，即可通过一元线性拟合计算出斜率b1，进一步得到散热系数K=b1.

经实验测定，散热系数K的数值约为10-5数量级（参见2.1计算结果）.由于K的数值很小，在一定时间范围内可以对式（7）中指数函数项e-Kt进行泰勒展开并保留前两项，得

将式（9）代入式（7），并化简可得

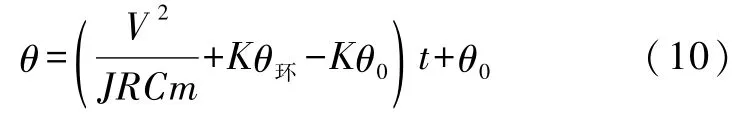
向实验装置中加入一定量的水，并通电加热，测量一段时间内温度θ与时间t的关系（注意实验系统与环境的温差始终保持在牛顿冷却定律适用范围内）.对θ与t进行一元线性回归，得到斜率b2=，截距a2=θ0.则有

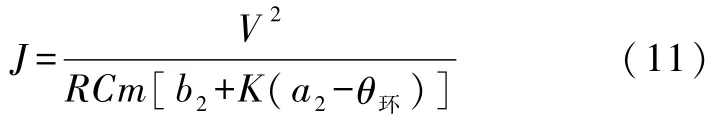
1.2 误差分析

下面讨论实验中两个主要的误差，并控制其在合理范围内.

1）泰勒展开带来的误差.显然，总时间越长，展开带来的误差越大，如图2，令l1为实际的θ-t关系，则近似之后得到的直线为l2，其中，Δθ是时间为t时近似带来的误差，θ为t时间内温度的变化.则

图2 θ-t关系

假设l1为一条直线（实际是弧度极小的曲线），斜率为k，则b2的相对误差为

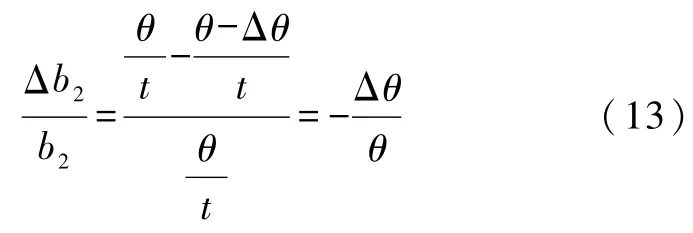
对式（11）两边取对数并求导得

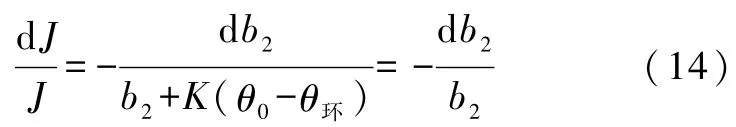
上式中，可由实验数据证明K（θ0-θ环）约为b2的1%，这里仅为近似计算误差，所以可以忽略.于是得到

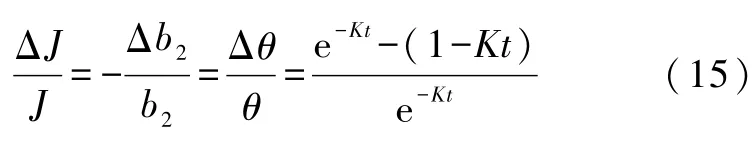
2）温度计示值误差.本实验使用金属铂电阻温度计，示值误差约为0.2℃.t时刻读取温度的相对误差为

显然，σ是一个关于t的减函数，只需令t=0时，σ＜1%，即可保证任何时刻温度读数的相对误差小于1%.计算得θ0＞20℃，所以实验的起始温度需要在20℃以上.

1.3 误差分析的验证

用上述实验中得到的数据分别选取不同总时长进行一元线性拟合，并由式（11）求得不同总时长下的热功当量值J，由此做出热功当量相对误差与总测量时间的关系如图3所示.

由图3可见，当总时长小于300 s时，热功当量的测量值与标准值1的相对误差较大，这是因为实验装置本身的误差（温度计的示值误差等）在总时间过小时对实验的影响不可忽略.当总时长大于500 s时，热功当量的测量值与标准值的误差随总时长的增加而增加.这与“泰勒展开带来的实验误差随总时间的增加而变大”的结论相一致.当总时间在500 s时，热功当量的实验测量值与准确值的相对误差最小，是最适合在实验中应用的总时长.由此，实验验证的结果与理论分析完全一致，从而验证了实验原理与误差分析的正确性.

图3 热功当量测量值的相对误差与总测量时间的关系

2 实验结果

2.1 K值的测量

向实验装置中加入高于环境温度（不超过牛顿冷却定律适用范围）的一定量的水，在不加热情况下测定50 min内温度随时间变化的规律，每5 min记录一次温度，并且记录实验前后环境温度，取平均值作为真正的环境温度θ环，测量数据及部分计算结果如表1所示.

表1 K值的测量数据

令yi≡ln（θ1i-θ环）、，xi≡t，进行一元线性拟合，得到斜率b1=-8.32×10-5s-1，u（b1）=-0.19×10-5s-1.即有K=-b1=8.32×10-5s-1，u（K）=0.19×10-5s-1.

2.2 热功当量J的测定

给定值电阻两端加一定电压使实验装置加热，每隔30 s记录一次系统温度，测量数据如表2所示.

始末环境温度求得平均值θ环=26.898℃、负载电压V=39.875 V、电阻阻值R=201.9 Ω、内桶质量m1=131.33 g、水质量m0=218.13 g，内桶比热容c1= 0.389 J/（℃·g）、水比热容c0=4.18 J/（℃·g）、加热器热容c2m2=64.38 J/℃，前已测得散热系数K=8.32×10-5s-1.

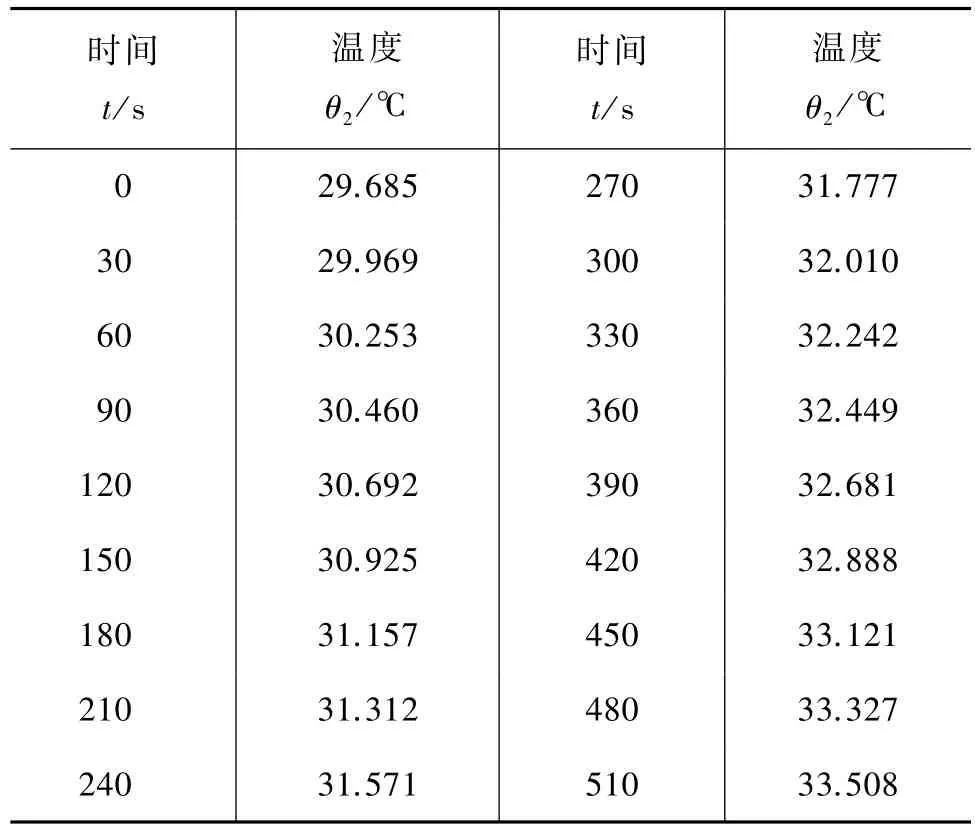
表2 热功当量测量数据

对实验数据进行一元线性回归，拟合得到斜率b2=0.00742，u（b2）=0.00005；截距a2=29.777，u（a2）=0.015；相关系数r=0.9996.将b2、a2值代入式（11），可得热功当量值J=1.0011，相对误差η=0.11%.

对实验结果进行不确定度的分析和计算.由式（11）可得

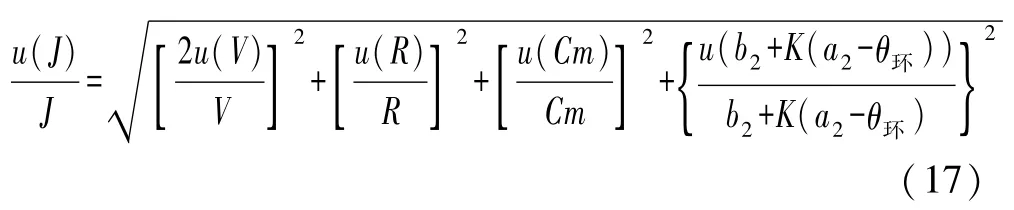
其中V、R、Cm、θ环的误差均可略，则

所以，热功当量的最终表述为J±u（J）=1.001±0.007.

3 结论

本文采用“积分法泰勒展开取近似”取代“差分代替微分近似”来修正系统散热，解决了“差分代替微分是否合理”的争议.上述方案中，近似带来的实验误差是可以计算的，并且通过控制总时间可以把误差限制在合理范围内.

通过泰勒展开可以得到温度θ与时间t的线性关系.利用一元线性回归拟合线性关系时用到多组数据，这样计算热功当量的实验方案实验准确度更高，实验结果更加可靠.

［1］《大学物理实验》编写组.大学物理实验［M］.北京：清华大学出版社，2008：126-128.

［2］张捷民，刘汉臣.大学物理实验［M］.北京：科学出版社，2007：140-141.

［3］代伟，李骏，陈太红，等.电热法测热功当量实验的改进［J］.西华师范大学学报，2011，32（1）：95-97.

［4］洪履燊，等.热功当量测量实验的改进方法［J］.福州大学学报（自然科学版），2007，35（z1）：106-108.

［5］李朝荣，徐平，等.基础物理实验（修订版）［M］.北京：北京航空航天大学出版社，2010：117-118.

A new exploration in determination of mechanical equivalent of heat by electrothermal method

CAI Chen，LI Chao-rong，LI Ying-zi，WANG Xuan
（School of Physics and Nuclear Energy Engineering，Beihang University，Beijing 100191 China）

A new experimental method is proposed to resolve the heat dissipation problem of the device in determination of mechanical equivalent of heat by electrothermal method.Based on integral method，the result of mechanical equivalent of heat is more close to the theoretical value，and the data exhibits strong linear relationship through simple linear regression.

mechanical equivalent of heat；coefficient of heat transfer；linear regression；correlation coefficient

O 43

A

1000-0712（2016）05-0053-04

2015-10-07；

2015-11-18

蔡晨（1994—），男，河北涿州人，北京航空航天大学物理科学与核能工程学院2013级本科生.