二端RC梯形网络的等效复阻抗研究

方靖淮，李红兵，谭志中

（南通大学理学院，江苏南通 226019）

二端RC梯形网络的等效复阻抗研究

方靖淮，李红兵，谭志中

（南通大学理学院，江苏南通 226019）

复阻抗网络不同于纯电阻网络，其电路元件的变化对等效复阻抗带来的影响比较大.本文采用建立非线性差分方程模型的方法研究了二端梯形RC复阻抗网络的等效复阻抗公式.根据可能存在的不同条件，采用复数分析方法研究了RC梯形网络的等效复阻抗在不同条件下的普适规律，自然地得到纯电容网络的等效电容公式.

RC梯形网络；非线性差分方程；等效复阻抗；普适规律

自从1845年德国物理学家基尔霍夫发现了节点电流定律和回路电压定律以来，电阻网络模型的建立与研究已经有170多年的历史［1］.由于电阻网络模型具有多价值功能，已经被应用于许多科学和工程技术领域，其研究工作有很重要的理论与应用意义［1-24］.文献［1-9］研究了不同条件下的电阻网络的等效电阻问题，得到了比较理想的结果.复阻抗网络问题的研究比纯电阻网络研究复杂得多，所得结论也复杂得多.与电特性有关的许多材料一般可以等效为电路网络.传输线是用来传送电能或电信号的，任何电子设备都需要使用传输线，最典型的传输线是两根平行的铜线或同轴电缆.在电磁场理论、光电系统、电路理论、微波网络技术、数学物理方法等研究中［10-21］，都存在对传输线问题的研究，但这些研究通常都是建立微分方程（电报方程）的方法.文献［22-24］的研究推动了复阻抗网络的研究与应用.文献［20］主要研究了LC网络的等效复阻抗问题，目前对于n阶RC梯形网络的等效复阻抗问题尚缺乏详细研究.本文拟采用建构差分方程的方法以克服微分方程（略去了二阶无穷小量而得到的近似方程）之不足.我们用构建非线性差分方程模型的方法对梯形RC网络的等效复阻抗问题进行全面而系统的研究，得到了一些具体的普适公式.

1 RC网络与数学模型

如图1所示电路是一般形式的二端RC梯形复阻抗网络，其中R为电阻，C1和C为电容，Z0为负载.我们的目标是研究左端an、bn两节点间的等效复阻抗公式，同时分析其在不同条件下的具体特性.

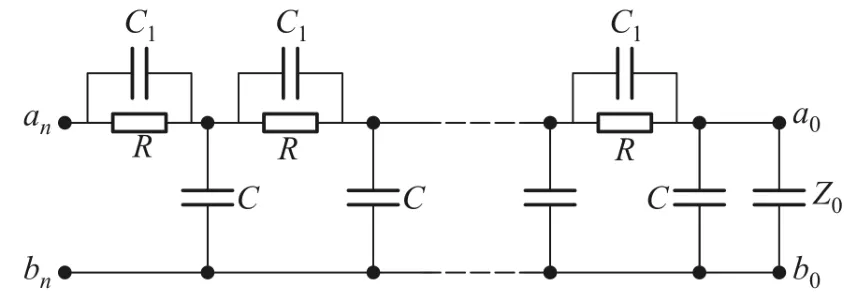
图1 二端RC梯形网络模型

可以认为图1是由n个网络单元构成的网络结构，根据文献［1-20］的研究策略，不难得到关于图1的等效模型图，如图2所示.如果输入电压的圆频率为ω，则电容C产生的阻抗为ZC=1/（jωC）.其中j为虚数单位，j2=-1.

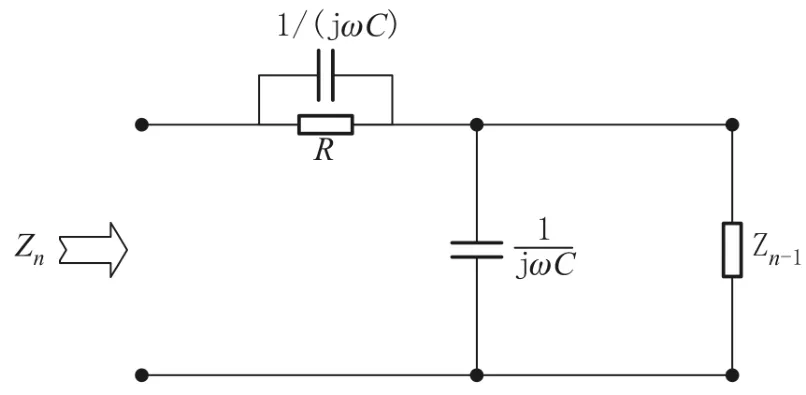
图2 等效RC网络模型

记图1所示的n阶网络左端an、bn为输入端，并且输入端等效复阻抗值记为Zn，则n-1阶网络输入端等效阻抗可记为Zn-1.在图2中根据串联和并联复阻抗的计算方法得到

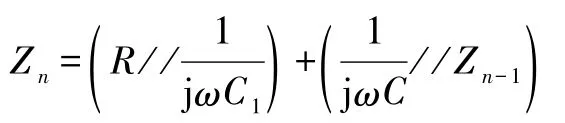
其中//表示并联计算，由此化简得到

式（1）是关于等效复阻抗值的非线性差分方程模型.根据文献［1］中建立的非线性差分方程研究方法可以求出方程式（1）在各种情形下的通解.下文的工作主要就是研究非线性差分方程（1）的通解.

2 非线性差分方程的通解

本文拟采用文献［1］中建立的变量代换的方法研究非线性差分方程式（1）的通解.设存在待定数列，且xn满足如下关系：

其中约定x0=1，则x1的值由式（2）确定为x1=Z0，这也是网络右端的负载.

将式（1）中的常数项移至方程的左端得到

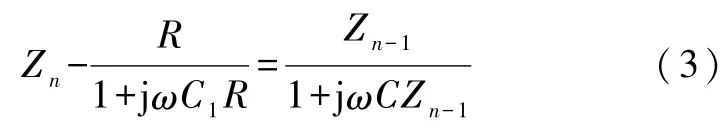
将式（2）及其递推式代入式（3）得

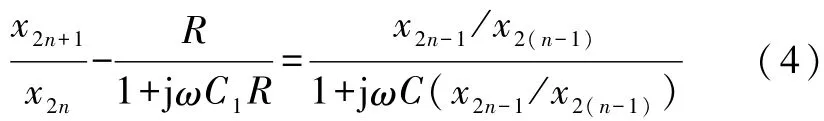
将上式化简并将右端分子与分母分别同时乘以一个待定系数a得（这一技巧很重要，这一方法也是文献［1］建立的创新）

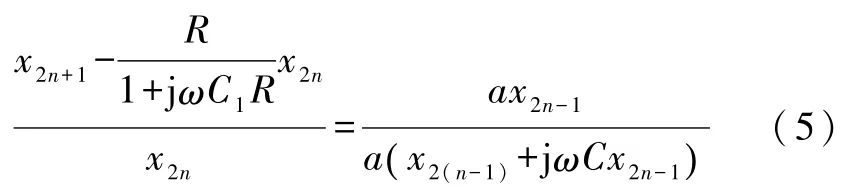
分别令式（5）左端与右端分子相等、分母相等（恒等式），得到

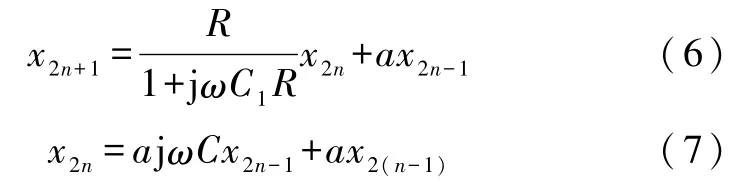
为了使以上2式具有相同的结构，设式（6）与式（7）的对应项系数相等得到

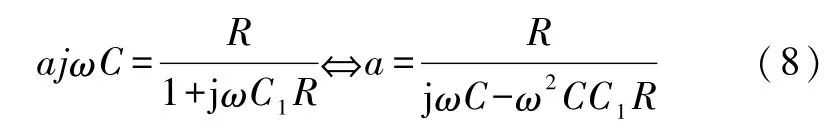
比较以上二式不难发现：方程式（6）和式（7）中的数列｛xn｝满足下列统一的递推关系：

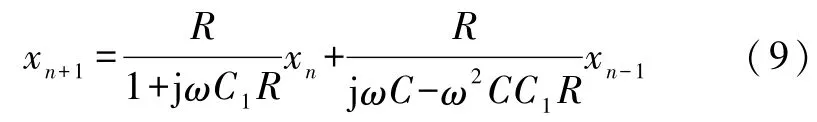
即式（9）包含了式（6）和式（7）两个方程（这一方法的正确性可以参见文献［1］中给予的证明）.不难发现：式（9）是一类二阶线性差分方程，由式（9）得其特征方程

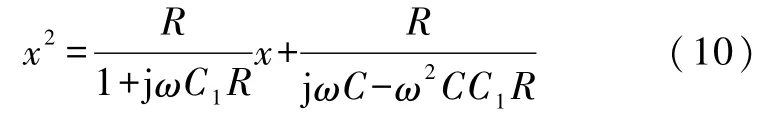
设方程式（10）的两个根分别为α和β，解该方程得

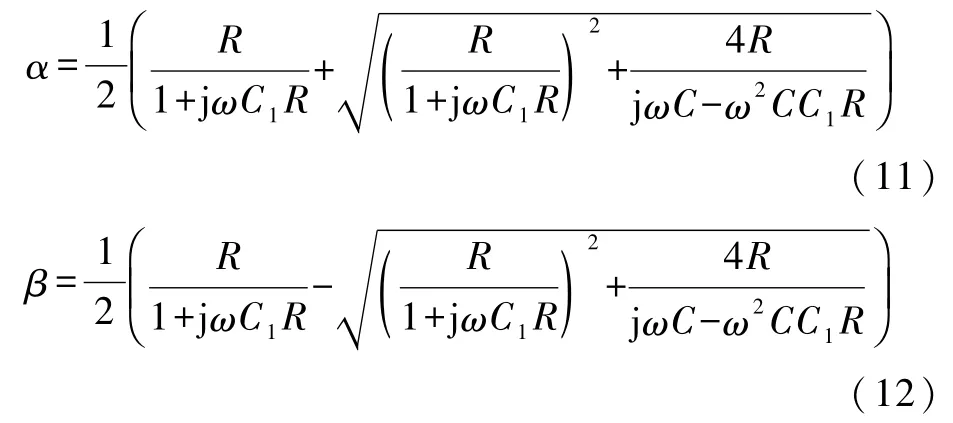
根据文献［1］解差分方程的方法解差分方程式（9）得

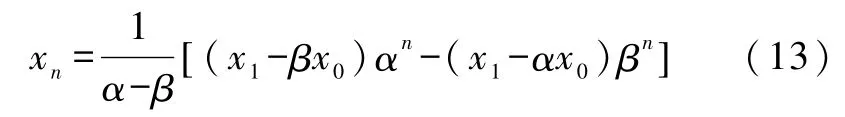
将式（13）及其递推式代入式（2）并注意应用x0=1，x1=Z0得

其中n=0，1，2，….特别地式（14）还可以重新写成

或者

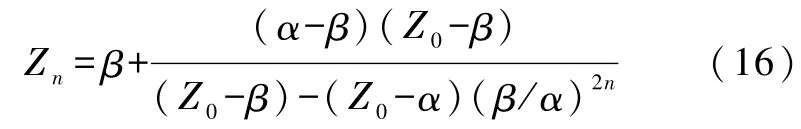
式（14）—式（16）即为非线性差分方程式（2）的通解.我们可以进行简单验证其正确性.如设n=0代入式（14）得到：左边=右边=Z0，显然成立.当然，由于以上推导是严格的和自洽的，其理论计算结果必然是正确的.不难发现式（14）不仅形式优美对称，而且结论简洁，是一次理论创新.式（14）是Z0为任意负载情形时的普适公式.由于复阻抗不同于纯电阻而具有复杂性，下面将继续研究RC网络的负载为特殊情形时的基本特性.

3 几个特殊情形

情形1.当Z0=α时，由式（15）得到Zn=α.

情形2.当Z0=β时，由式（16）得到Zn=β.

情形3.当Z0=α+β时，由式（14）得到

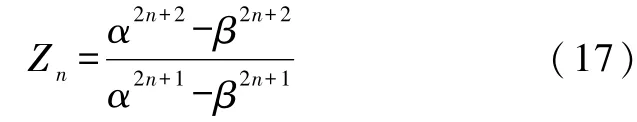
情形4.当Z0=0（短路）时，由式（14）得到

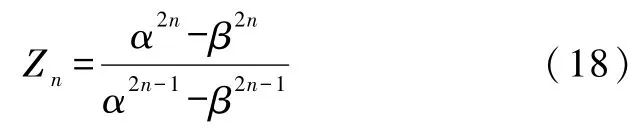
情形5.当Z0=∞（开路）时，由式（14）得到

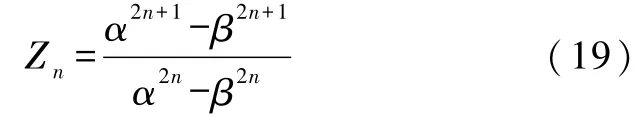
请注意，式（17）—式（19）结构相似，但是存在差别.

4 RC网络的等效复阻抗特性

4.1 复变函数分析

首先分析α、β的特性，由式（11）化简得到

其中由

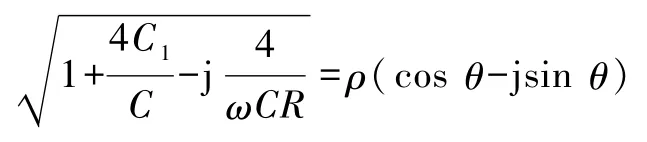
解得

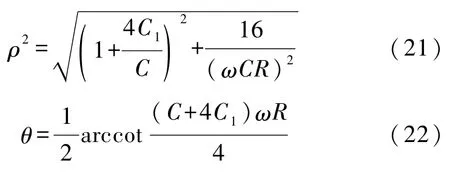
由式（20）化简得到

其中

以及

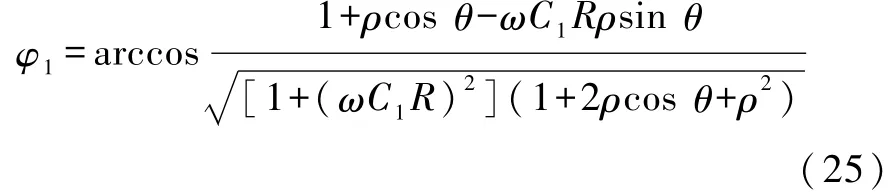
同理得到

其中

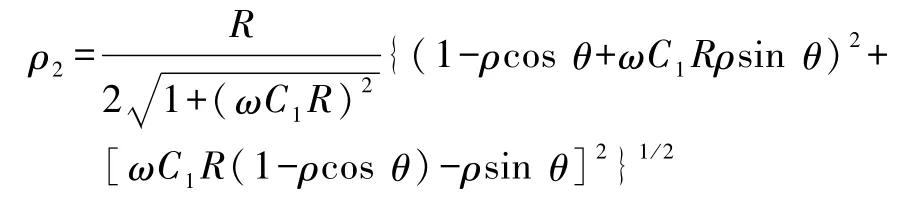
进一步化简得到

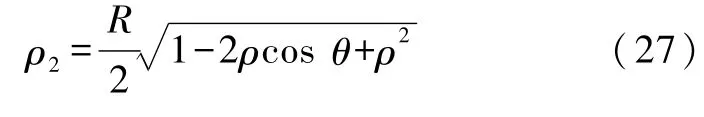
以及

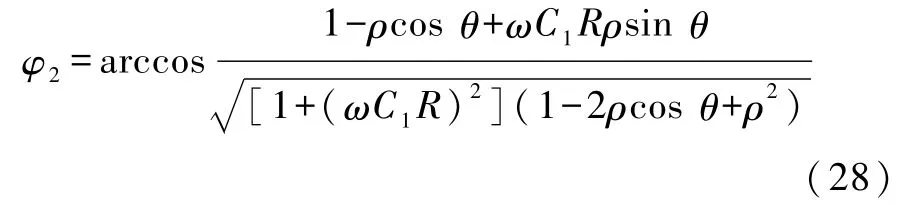
将式（23）、（26）代入式（16）于是得到

其中

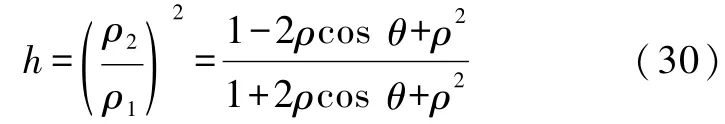
4.2 当R→∞时的电容网络

当R→∞时表明图1为纯电容网络，由式（11）、（12）得到

则有

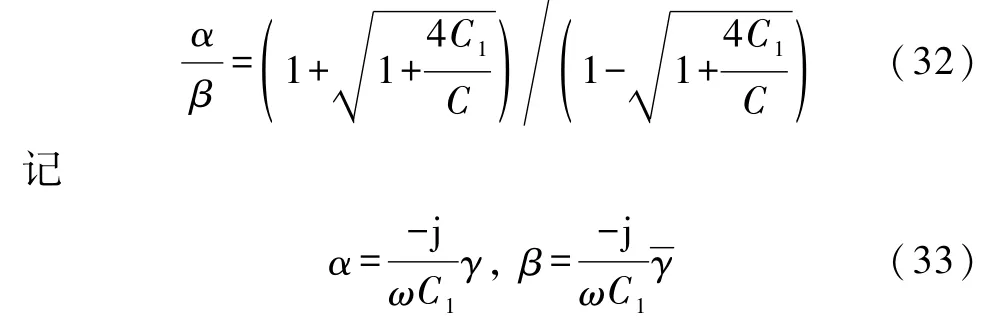
将式（33）代入式（14）得到

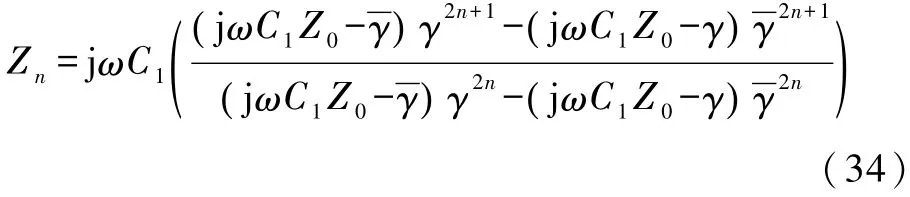
其中

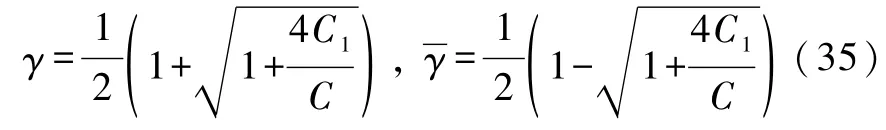
如果右端负载Z0也是由电容构成的，如Z0= 1/jωC2，则式（34）为纯虚数.可得到电容网络的等效电容公式

4.3 当C1=0时的情形

当C1=0时，表明电容线路处于断路状态，则图1所示的电路退化成为图3所示的电路.这时方程式（10）的两个根α和β退化为

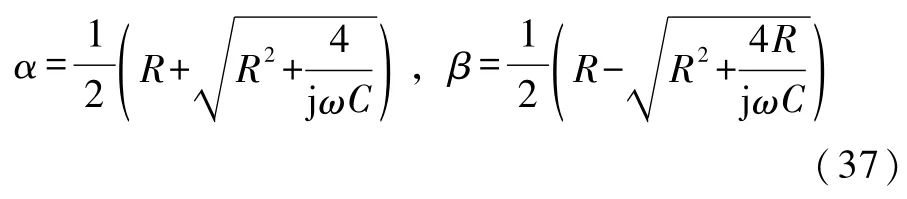
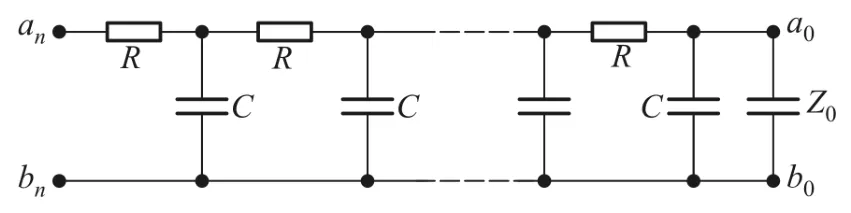
图3 二端RC梯形网络模型

由式（29）可得到

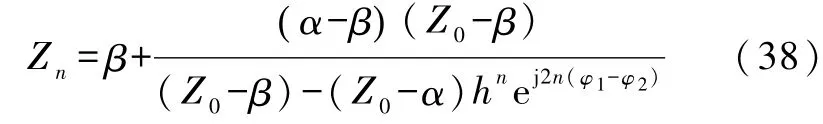
其中h由式（30）给出，并且

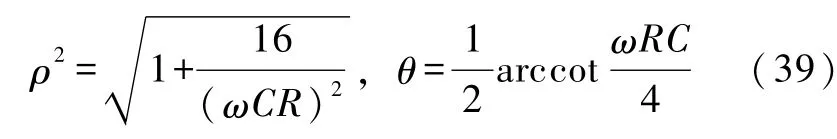
以及

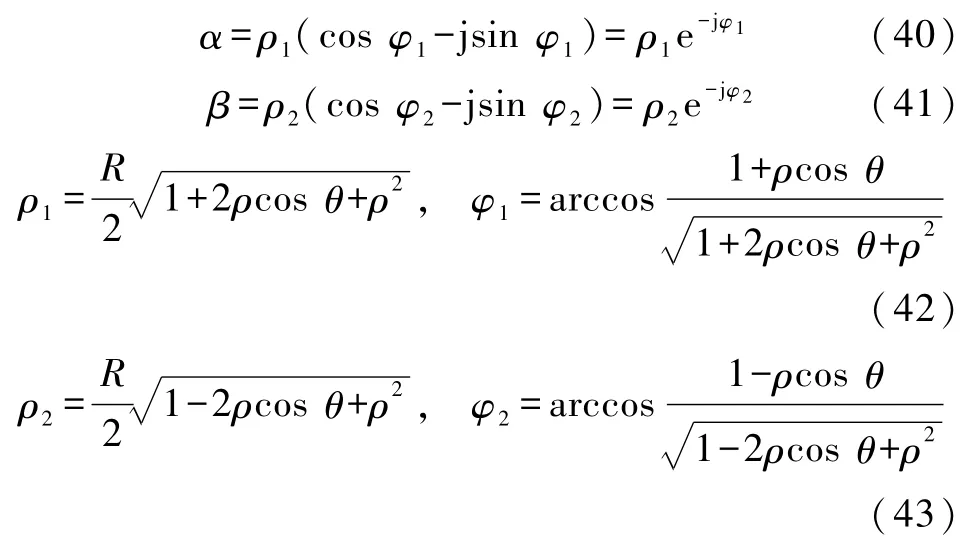
4.4 当n→∞时的情形

当n→∞时，由式（22）得知0＜θ＜π/4，所以

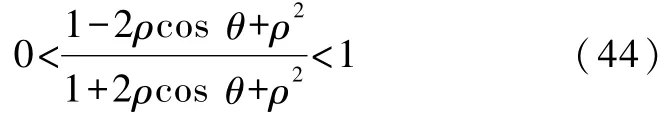
所以

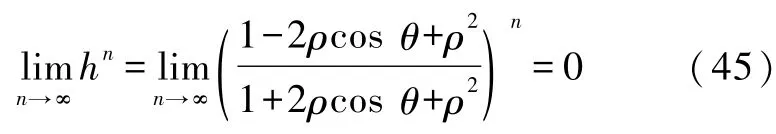
因此，将式（45）代入式（38）得到

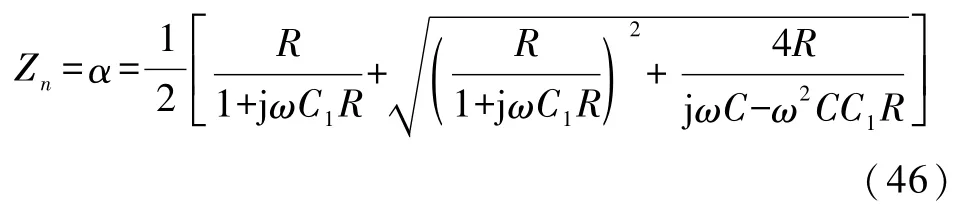
式（46）是一个很有趣的结果，是一个有限常数，其等效复阻抗仅仅由特征方程的根表达.

5 小结与讨论

通过构建非线性差分方程模型研究了二端梯形RC网络等效复阻抗的一般规律及其不同情形时的解析解.首先建立等效的RC网络模型构建非线性差分方程模型式（1），研究非线性差分方程式（1）的通解是解决问题的关键.我们采用变量代换的方法式（2）以及恒等变换方法式（5）获得了非线性差分方程式（1）的通解式（14）、（15）和式（16）.由于复阻抗网络的复杂性，我们接着详细研究了通解式（14）在不同情形下的特殊结论.特别是采用复数分析方法给出了更为实用的结论式（29），并且给出了纯电容网络的等效电容公式（36）.

本文的研究工作是一次理论和方法上的创新，因为方程式（4）与式（9）的构建是我们的创新研究，这种创造性的工作大大简化了我们的计算过程，所得到的全部结论也都是本文第一次给出，为科学工作者和工程技术人员提供了应用研究及计算机仿真研究的理论根据.另外本文的研究也为大学物理开展科学探究教学提供了很好的教学案例，对培养大学生的创造性思维能力具有积极意义.构建非线性差分方程模型的方法是一种比较简洁的研究方法，如何研究高阶的m×n阶复阻抗网络的等效复阻抗问题有待进一步研究.

［1］谭志中.电阻网络模型［M］.西安：西安电子科技大学出版社，2011.

［2］陆建隆，谭志中.关于梯形网络等效电阻的普适研究［J］.大学物理，2001，20（10）：26-28.

［3］张小溪.规则连接的电阻、电容网络的数学模型［J］.大学物理，1999，18（2）：28-31.

［4］谭志中，赵素英.N阶电阻网络等效电阻的普适研究［J］.河北师范大学学报（自然科学版），2004，28（2）：149-154.

［5］谭志中，陈翠萍.8×n阶矩形网络的等效电阻和电容及2个猜想［J］.河北师范大学学报（自然科学版），2013，37（6）：579-586

［6］Tan Z Z，Essam J W，Wu F Y.Two-point resistance of a resistor network embedded on a globe［J］.Phys Rev E，2014，90：012130.

［7］Tan Z Z，Fang J H.Two-point resistance of a cobweb network with a 2r boundary［J］.Commun Theor Phys，2015，63：36-44.

［8］Tan Z Z.Recursion-transform approach to compute the resistance of a resistor network with an arbitrary boundary［J］.Chin Phys B，2015，24：020503.

［9］Tan Z Z.Recursion-transform method to a non-regular m×n cobweb with an arbitrary longitude［J］.Scientific Reports，2015，5：11266.

［10］潘咏梅，徐善驾.非理想导波结构损耗特性的等效传输线法分析［J］.微波学报，2004，20（2）：40-44.

［11］章日荣.波导阻抗原理及应用［J］.无线电通讯技术，2001，27（2）：46-49.

［12］李瀚荪.电路分析基础［M］.北京：高等教育出版社，1983：883-896.

［13］刘鹏程，邱扬，等.电磁兼容原理及技术［M］.北京：高等教育出版社，1993.

［14］黄志洵，王晓金，等.微波传输线理论与实用技术［M］.北京：科学出版社，1996.

［15］梁昆淼，刘法，缪国庆.数学物理方法［M］.北京：高等教育出版社，1998：199-201.

［16］陈崇源.高等电路［M］.武汉：武汉大学出版社，2000：306-308.

［17］王勇，龙建忠，等.电路理论基础［M］.科学出版社，2005：376-378.

［18］肖哲，黄铭，等.三维RC网络仿真异质材料的通用介质响应［J］.物理学报，2008，57（2）：957-961.

［19］孙俊，肖哲，等.基于RC网络的非均匀介质模型研究［J］.电子测量技术，2007，30（4）：136-138.

［20］谭志中，陆建隆.二端梯形网络等效复阻抗的普适研究［J］.大学物理，2009，28（7）：29-33.

［21］鲁百佐.传输导线等效电阻与频率的关系研究［J］.西安石油学院学报（自然科学版），2003，18（4）：80-82.

［22］Alioto M，Palumbo G，Poli M.An Approach to Energy Consumption Modeling in RC Ladder Circuits［M］.Heidelberg：Springer Berlin，2002：413-428.

［23］Sanjit K.Mitra.A new approach to active RC network synthesis［J］.Journal of the Franklin Institute，1962，274（3）：185-197.

［24］Tzeng W J，Wu F Y.Theory of impedance networks：the two-point impedance and LC resonances［J］.J Phys A：Math Gen，2006，39：8579.

Study on equivalent complex impedance between two terminal nodes in the RC ladder network

FANG Jing-huai，LI Hong-bing，TAN Zhi-zhong
（School of Science，Nantong University，Nantong，Jiangsu 226019，China）

The complex impedance network is different from the pure resistance network，and the change of the circuit element has a great influence on the equivalent complex impedance.In this paper，the equivalent complex impedance formula of the two terminal RC complex impedance network is studied by using the method of establishing the model of nonlinear difference equation.According to the different conditions of the potential，the universal formula of the equivalent complex impedance of RC ladder network under different conditions is studied by using the complex analysis method，and the equivalent capacitance formula of pure capacitance network is obtained naturally.

RCladdernetwork；nonlineardifferenceequation；equivalentcompleximpedance；universal formula

O 441.1，TN 711.3

A

1000-0712（2016）05-0014-05

2015-09-14；

2015-11-12

江苏省产学研联合创新资金—前瞻性联合研究项目（BY2014081-06）、江苏省高校自然科学研究面上项目（14KJB140012）资助课题、南通大学教学改革研究项目（2014B9）资助

方靖淮（1962—），男，江苏淮安人，南通大学理学院教授，博士，主要从事理论物理教学与研究工作.