基于IOWA的中国海洋生物医药业组合预测模型的应用研究

郑　莉，张玉洁，李琳琳

（国家海洋信息中心，天津 300171）

【统计与分析】

基于IOWA的中国海洋生物医药业组合预测模型的应用研究

郑莉，张玉洁，李琳琳

（国家海洋信息中心，天津 300171）

基于诱导有序加权平均算子的组合预测方法是近年来发展起来的具有广泛应用的预测模型。首先采用指数平滑模型、ARIMA模型及多元回归模型建立了中国海洋生物医药业增加值的单项预测模型；随后引进诱导有序加权平均 （IOWA）算子的概念，建立了海洋生物医药业增加值的组合预测模型，实证结果表明组合模型能有效提高预测精度；最后利用组合模型对 “十三五”期间中国海洋生物医药业发展趋势进行了预测分析。

海洋生物医药业；诱导有序加权平均算子；组合预测；海洋经济；海洋产业

引言

中国海洋自然条件优越，海域辽阔，大陆海岸线长达18 000多千米，海洋资源种类繁多，海洋生物资源储备丰富。中国现代海洋药物的研究始于20世纪70年代，随后海洋生物药物产业也快速发展起来，产生了可观的经济效益。当前中国海洋生物产业处于起步向全面产业化发展的关键时期，随着国家对海洋生物医药业政策扶持和投入力度的逐步加大，海洋战略性新兴产业中的海洋生物医药业发展正行驶在快车道。适时加快对海洋生物医药业发展的宏观分析与预测研究对于确定全国海洋生物医药业增长目标和海洋开发战略将具有重要的实践和参考意义。本文将以海洋战略性新兴产业——海洋生物医药业为例，对海洋生物医药业增加值建立动态组合预测模型，为其它海洋产业发展趋势预测提供一定的借鉴。

1　诱导有序加权组合预测模型简介应用情况

国内外许多学者和机构都对海洋生物医药业的预测方法进行了广泛研究，主要方法为时间序列分析法、灰色预测法、情景分析法等，但组合预测的文献较少。组合预测可以综合利用各种预测方法所提供的信息，提高预测的精确度和可靠性。Bates和Granger（1969）［1］首次提出了组合预测的概念，即通过确定各单项预测方法的加权平均系数，以适当权重将不同的单项预测方法进行组合。基于组合预测的思想，Yager（1999，2002）［2，3］提出诱导有序加权平均（IOWA）算子，通过引入IOWA算子，根据各单项预测方法在样本区间上各时点的拟合精度的高低按顺序赋权，以误差平方和为准则建立一种动态组合预测模型。国内学者陈华友（2003，2005）［4，5］最先使用诱导有序加权的预测方法，并证明该方法相比于传统的广义加权算术平均组合预测方法具有更高的精度，各种预测误差指标值均低于传统方法。这种方法克服了传统静态组合预测模型在集成时存在对单项预测方法以固定权系数赋权的缺陷，可以对不同时期的单模型预测结果进行动态集成。

诱导有序加权平均组合预测模型基本计算过程如下［4-6］。

1.1计算预测精度

设某经济现象的指标序列有观察值为 ｛yt，t=1，2…，N｝，有m种可行的单项预测方法，设yt为第t时刻的真实值，为第t时刻第种方法的预测值。i=1，2，…，m；t=1，2，…，N。w1，w2，…，w3为单项预测方法在组合预测中的加权系数，满足

称ait表示第i种预测方法第t时刻预测精度，或预测值的诱导值，若：显然，ait∈［0，1］预测度反映了预测模型的拟合值与实际值拟合程度的优劣。

1.2确定IOWA算子组合预测值

将ait看成的诱导值，构建m个二维数组并按从大到小的顺序排列预测精度序列a1t，a2t，…，amt，对排序后的预测值分别赋以权重。则可确定IOWA算子的组合预测值：

式中：a-index（it）是第i个大的预测精度的下标，W=（W1，W2，…，Wm）T为各单项预测方法在组合预测中的IOWA算子的加权向量。显然，新的组合预测的赋权系数与单项预测方法在各时点上的预测精度大小密切相关，预测精度高就优先赋大一点的权系数。

1.3建立基于IOWA算子的组合预测模型

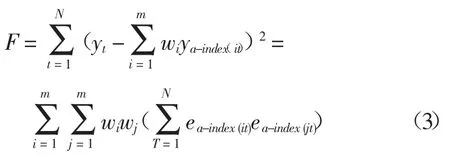
式中：R=（1，1，…，1）T，W=（W1，W2，…，Wm）T，上述规划实际上是一个二次规划，可利用Kuhn-Tucker条件将其转化为线性规划或直接用matlab最优化工具箱来求解出最优权系数

1.4基于IOWA算子的组合预测模型的预测

通过上文二次规划模型求解可以获得样本区间上组合预测IOWA最优权系数，设W*=根据预测连贯性的原则，可进行预测区间［N+1，N+2，…］的基于IOWA算子组合预测，公式为：

式中：t=N+1，N+2，…，在预测区间 ［N+ 1，N+2，…］上，a1t，a2t，…，amt（预测精度序列）的大小是根据各单项预测方法在样本区间上近几期拟合平均精度的高低来确定。即要进行未来k步的预测时，用第i种预测方法最近的k期拟合平均精度来反映预测区间上第期的预测精度。

在应用方面，胡彦（2009）［7］等建立基于IOWA算子的税收组合预测模型，夏立福等（2011）［8］以实际工程为例，将IOWA算子组合预测结果与单一模型结果进行比较，验证了IOWA算子组合预测方法的实用性。吴凤平（2013）［9］采用BP神经网络和GM（1，1）作为单项预测模型，对连云港港口吞吐量建立了基于IOWA算子的组合预测模型，并验证了该模型预测精度优于各单一预测模型，各项误差指标都低于其他两种预测方法。尽管IOWA算子组合预测方法具有比传统预测方法更精确，更稳定的预测结果，但基本尚未应用在海洋经济预测领域，本文拟在海洋经济领域引入IOWA算子的组合预测模型，选取海洋生物医药产业为例，对海洋生物医药业增加值建立动态组合预测模型。

2　中国海洋生物医药业增加值预测实证研究

下文将对中国海洋生物医药业增加值建立指数平滑模型、ARIMA模型及多元回归模型3种模型，并在此基础上进行组合预测研究［10-12］。其中，建模数据来源于《中国海洋统计年鉴》（2002—2014年）及《2014年中国海洋经济统计公报》。图1描述了中国海洋生物医药业增加值走势（2001—2014年）。

图1　2001—2014年中国海洋生物医药业增加值Fig.1　The added value of China's marine biomedicine industry from 2001-2014

2.1单项预测模型

2.1.1指数平滑模型

指数平滑法适用于不具有明显的季节波动和趋势变动的单指标时间序列数据。指数平滑法分为单指数平滑法、双指数平滑法、Holt-Winters乘法模型、Holt-Winters加法模型和Holt-Winters无季节性模型，其中Holt-Winters无季节性模型适用于具有时间趋势但无季节变化的序列，对于中国海洋生物医药业增加值数据序列yt，可以采用这种方法进行预测，yt平滑后的序列y^t的计算式为：y^t+k=at+btk，k＞0，其中at表示截距，bt表示斜率，这两个参数定义为下列递归式：

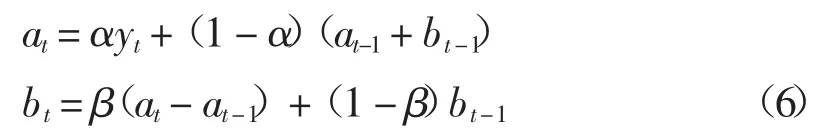
式中：α、β取值在［0，1］之间，称之为阻尼因子。预测值就可以由下式计算：

利用2001—2014年海洋生物医药业增加值数据，利用Eviews软件建立Holt-Winters无季节性模型，得到α、β值分别为1、0.57。通过上述指数平滑模型得到2003—2014年中国海洋生物医药业增加值见表1。

2.1.2ARIMA模型

ARIMA模型是被广泛运用于对各类时间序列数据分析和建模的方法。模型基于如下的观念：要预测的时间序列是由某个随机过程生成的。如果生成序列的随机过程不随时间变化，则该随机过程的结构可以被确切地刻画和描述。利用序列过去的观察值，可以外推出序列的未来值。在ARIMA模型中，序列的未来值被表示成滞后项和随机干扰项的当期及滞后期的线性函数，即模型的一般形式如下式所示：

上述模型称为ARIMA（p，d，q）模型，其中，Yt是d阶单整序列，由一个自回归模型AR（p）和一个移动平均模型MA（q）组成，p为模型的自回归项数，q为模型的移动平均项数。其中，Yt是自回归移动平均序列，c为常数，α1，…，αp表示自回归系数，β1，…，βq表示移动平均系数，εt是相互独立的白噪声序列。

根据上述建模过程，利用2001—2014年数据，对中国海洋生物医药业增加值序列建立ARIMA（0，2，2）模型，方程估计结果如下：

采用上述建立的ARIMA模型并通过静态预测法，可得到2003—2014年中国海洋生物医药业增加值见表1。

2.1.3多元回归模型

多元回归模型的基本表达式如下：

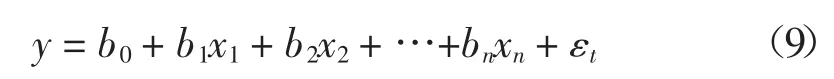
式中：y为因变量，x为自变量，b0，b1，…，bn为待估计参数。最常见的参数估计方法为最小二乘估计法。多元回归模型包括线性回归及非线性回归，有多种变形，其中自变量可取对数、指数、幂指数等多种形式。

本文将对中国海洋生物医药业增加值建立基于生产函数的回归方程并预测。回归方程的解释变量包括资本投入、劳动力投入。由于海洋生物医药业时间序列较短，本文假定规模报酬不变即α+β=1，通过对C-D生产函数的一般形式进行变形（其中，Y、K、 L分别表示产出量、资本、劳动投入量，α、β分别表示资本、劳动的产出弹性，A0为常数，表示基年的技术水平，r也是常数，表示科技进步增长速度，t表示时间，A0ert表示t年的综合科技水平），得到新的形式这一模型形式可以节省自由度。从图1可以看出，2009年中国海洋生物医药业增加值减少，究其原因，主要是受2008年的金融危机的影响。为了能够捕捉到突发事件对回归模型的影响、提高预测精度，本文在回归模型中设置了虚拟变量dum09，将该变量2009年数值设置为1，其它年份设置为0。其中海洋生物医药业的资本变量没有统计数据，用沿海地区固定资本投入乘以海洋生物医药业增加值占全国海洋生产总值比重进行替代，建立如下回归模型：

采用多元回归模型得到的2003—2014年中国海洋生物医药业增加值见表1。

2.2基于IOWA算子的组合预测模型

用上述三种单项模型分别对中国2003—2014年的海洋生物医药业增加值进行预测，随后根据三种单项模型的预测结果建立基于IOWA算子的组合预测模型，并计算组合权重。根据式（1）可以得到三种模型在各个时点处的预测精度序列，从而可以构造出第t时刻预测精度和其对应在样本区间的预测值的二维数组如表1。

按式（2）对上表计算IOWA组合预测值，下面t=1，2以简要说明计算过程，当t=1时：

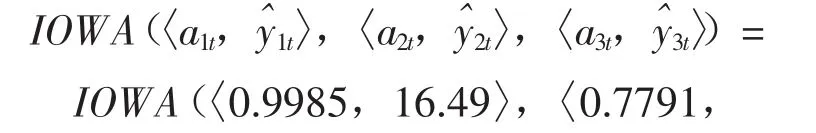
同理可得t=3，…，11的IOWA组合预测值，根据式（3）和式（4），得如下最优化组合模型：

对上式利用Matlab最优化工具箱计算得到基于IOWA的组合预测模型的最优权系数为：则在t时刻组合预测模型的预测值为：

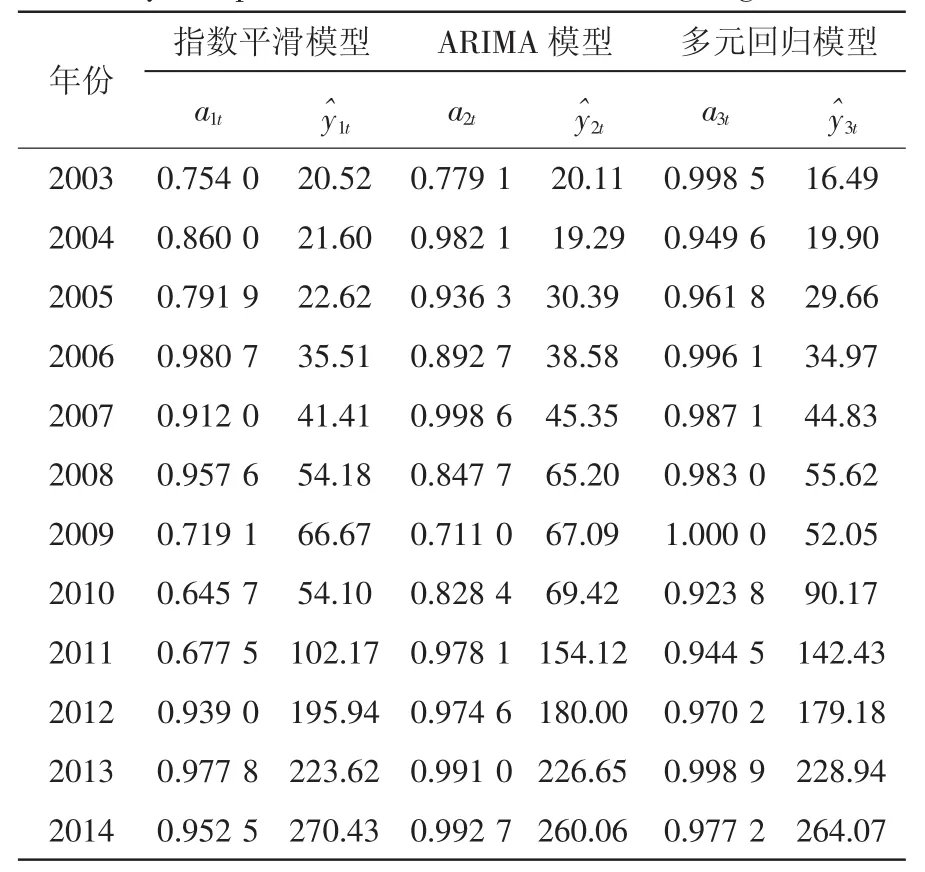
表1　三种单项预测方法预测精度及预测值二维数组Tab.1　Two-dimensional arrays consisting of prediction accuracy and predictive value of three forecasting methods

由上述组合模型知，时刻预测精度排名第二的单项预测法对应的权系数取值零，说明该时刻对应的单项预测方法冗余，这和传统的组合预测方法的权系数的计算有很大的不同。

2.3模型的评价及预测

一般模型比较方法有绝对数值比较和相对数值比较，其中均方根误差和平均绝对误差属于绝对数值比较，而平均绝对百分比误差和希尔不等系数属于相对数值比较［4-13］。由于均方根误差的应用原理与平均绝对误差基本一致，选一种即可，因此最终选择平均绝对百分误差、均方误差和希尔不等系数进行模型的评价。一般认为平均绝对百分比误差（MAPE）的值低于5%，则预测精度很高；均方根误差越小越好；希尔不等系数（Theil IC）的值介于0～1之间，且值越小，模型的精度越高。其中，

平均绝对百分比误差：

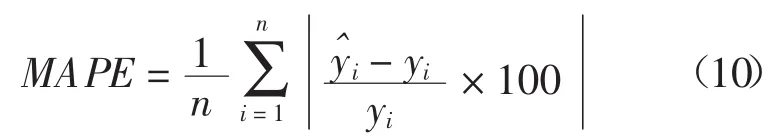
均方根误差：

希尔不等系数：

选取2003——2014年中国海洋生物医药业增加值单项模型预测及组合模型预测数据计算预测误差，从而进行模型评价，结果见表2及表3。由表2中结果可知，多元回归模型的MAPE值、RMSE值和Theil IC值较其它单项模型都小，且组合预测模型的MAPE值、RMSE值和Theil IC值均小于所有单个预测模型，同时也小于简单算术加权组合预测模型。由此可见，组合预测模型比单项预测模型的精度要高，同时比传统简单算术加权平均组合预测精度高，从而表明基于IOWA算子的海洋生物医药业增加值组合预测模型具有效性和优越性，是优性组合模型。从表3中结果可知，基于IOWA算子的组合模型具有很强的预测性，所有年份的预测误差均在5%以内。此外，由图2可看出，所有预测方法中，基于IOWA算子的组合模型预测值曲线与实际值曲线最为接近。

从前面的分析可得知，如果所选取的模型的信息具有很强的互补性，那么模型的预测误差将会更大幅度的降低，因此单项预测模型的选取在组合预测模型中是非常重要的。

表2　各个预测模型评价结果Tab.2　Evaluation results of each model

表3　基于IOWA算子的组合预测模型结果及评价Tab.3　Result and evaluation of the combined forecasting model based on the IOWA operator

图2　2003—2014年中国海洋生物医药业增加值实际曲线和拟合曲线Fig.2　The actual curve and fitting curve of the added value of China's marine biomedicine industry from 2003-2014

3　“十三五”时期海洋生物医药业预测及分析

根据上述单项模型及组合预测模型对2015至2020年中国海洋生物医药业增加值进行实证预测，其中，为了预测2015—2020年海洋生物医药业增加值，需要对回归模型中自变量进行预测，对于海洋生物医药资本变量预测采用ARIMA（1，1，1）模型预测，海洋生物医药业涉海就业人员采用指数平滑法预测。结果如表4所示。

表4　“十三五”时期中国海洋生物医药业增加值的预测值Tab.4　Forecast results of the added value of China's marine biomedicine industry during the 13th Five-Year Plan period　亿元

由表4知，预计到2020年，中国海洋生物医药业增加值将达到558亿元，“十三五”期间海洋生物医药业增加值的增速将达到14.6%（现价）。在国民经济新常态大背景下，随着中国海洋强国及海上丝绸之路战略的实施，经济体制改革和创新驱动的推进，以及国家和地方政府政策的大力支持，“十三五”期间中国海洋经济将逐步进入转型期，经济增长转入中高速、结构优化、效益提高、民生改善。海洋生物医药固定资产投资属于产业发展前期投入，由上文建立的多元回归模型可知，海洋资本的产出弹性为0.84，劳动力产出弹性为0.16，可见海洋生物医药业是资本密集型产业，符合海洋新兴产业发展特征，明显区别于传统海洋产业过分依赖于劳动力投入的发展模式。因此可以预期，作为海洋战略性新兴产业，海洋生物医药业将顺应国内外经济形势变化，增速将放缓。

4　结语

本文首次将IOWA算子组合预测方法引入到海洋经济预测领域，动态集成了指数平滑模型、ARIMA模型、回归模型三种方法对中国海洋生物医药业增加值数据进行了拟合，并对“十三五”期间中国海洋生物医药业的发展趋势进行了预测。在单模型预测时，本文的创新点在于在多元回归模型预测中，加入了突发事件虚拟变量，并对自变量采用了ARIMA模型进行预测。结果显示利用IOWA算子组合预测方法对其进行动态集成，集成后的误差得到了有效地控制，且全部控制在5%以内，预测精度较单项方法的预测精度得到大大提高。

但是，本文依然存在着一定的不足之处，可以在下一步的研究中进行创新和改进。首先，进行单模型预测时，由于本文预测对象可搜集到的数据较少，一些时间序列模型的预测效果并不是特别显著，可以尝试利用处理小样本的一些模型进行建模预测，达到提高预测精度的目的。其次，在组合预测时，本文采用了动态组合预测方法，大大降低了预测误差。但是，这种组合预测方法自身也存在一定的缺陷，比如说，在某些年份如果单模型预测结果都偏大，则最后组合预测的结果一定偏大，在今后的研究中将组合预测模型与专家意见集成对上述缺点进行改进将会是未来研究的一个方向。

［1］Bates J M，Granger C W J.The combination of forecasts［J］.Operational Research Quarterly，1969，20（4）：451-468.

［2］Yager R R.Induced ordered weighted averaging operators［J］.IEEE Transactions on Systems，Man，and Cybernetics，Part B，1999，29（2）：141-150.

［3］ Yager R R.Using fuzzy methods to model nearest neighbor rules［J］.IEEE Transactions on Systems，Man and Cybernetics，Part B，2002，32（4）：512-525.

［4］陈华友，刘春林.基于IOWA算子的组合预测方法 ［J］.预测，2003，22（6）：61-65.

［5］ 陈华友.组合预测方法有效性理论及其应用 ［M］.北京：科学出版社，2008.

［6］郭金童，赵光明.基于IOWA的中国能源需求组合预测模型的应用研究［J］.未来与发展，2010，1：68-72.

［7］胡彦，李秀美，陈华友．基于IOWA算子的税收组合预测模型［J］．统计与决策，2009（10）：33-35．

［8］夏立福，李井春，王洪海.基于IOWA算子的组合预测模型研究及应用 ［J］．测绘与空间地理信息，2011，34（1）：208-212.

［9］吴凤平，曹艳国.基于IOWA算子的港口吞吐量组合预测方法［J］.水利经济，2013，05：11-14+75.

［10］姜继娇，杨乃定．基于IOWA算子的行为证券组合投资决策研究［J］．系统工程理论与实践，2004（11）：57-62．

［11］王应用，罗英.广义加权算术平均组合预测技术研究［J］.预测，1998，17（1）：51～53.

［12］卢二坡.组合模型在中国能源需求预测中的应用 ［J］.数理统计与管理，2006，25（5）：505-511.

［13］丁晨芳．组合模型分析方法在中国粮食产量预测中的应用［J］．农业现代化研究，2007（1）：101-103．

Applied Research on Combined Forecasting Model of China′s Marine Biomedicine Industries Based on Induced Ordered Weighted Averaging Operators

Zheng Li，Zhang Yujie，Li Linlin
（National Marine Data and Information Service，Tianjin 300171，China）

The method of combination forecasting based on the induced ordered weighted averaging operator has been developed in recent years and used in a wide range of applications.Firstly，we respectively make use of exponential smoothing model，ARIMA model and multiple regression to construct models of added value of China′s marine biomedicine industry.Secondly，by introducing the concept of induced ordered weighted averaging operator，we construct the combination forecasting model of added value of marine biomedicine industry.The empirical results show that the combined forecasting model can effectively improve the prediction accuracy.Finally，we predict the development trend of China′s marine biomedicine industry during the 13th Five-Year Plan period by using the above combination forecasting model.

marine biomedicine industry；IOWA operator；combination forecasting

F224

A

2095-1647（2016）01-0038-08

2016-02-05

郑莉，女，助理研究员，主要研究方向为海洋经济统计、预测分析，E-mail：zhengli_668@126.com。