考虑孔隙曲折效应的浆液扩散压力
2016-10-24周子龙杜雪明赵云龙
周子龙,杜雪明,陈 钊,赵云龙,陈 璐
考虑孔隙曲折效应的浆液扩散压力
周子龙1,杜雪明1,陈 钊2,赵云龙1,陈 璐1
(1. 中南大学资源与安全工程学院,长沙410083;2. 广西翔路建设有限责任公司,南宁530029)
浆液扩散与压力变化情况是衡量注浆效果的重要参数,在传统的浆液扩散压力的研究中往往没有考虑被注介质孔隙通道的曲折效应,这造成计算得出的注浆压力值与实际值有明显的偏差。为此,根据分形理论推导出孔隙通道的曲折效应方程,并通过幂律流体本构方程导出考虑孔隙曲折效应的浆液扩散模型。分析孔隙曲折效应对扩散压力的影响,同时讨论了浆液黏度、流变指数以及单位注浆量对注浆压力衰减的影响规律。结果表明:若不考虑曲折效应,注浆压力随扩散距离的增大呈现缓慢衰减的变化趋势,若采用本研究中所推导的模型,其注浆压力随扩散距离的增大呈现急剧下降趋势;若考虑曲折效应,流变指数在特定的范围内,其压力损耗随流变指数的增大呈现首先急剧下降,之后变化幅度很小。
曲折效应;分形理论;注浆压力;扩散规律
注浆是将具有凝结和硬化性能的溶液通过注浆管以渗透、劈裂与挤密的方式注入到岩土介质中,通过驱赶岩土空隙中水分和空气、胶结改善岩土体的结构性能的一种工艺。因为它极强的实用性,已经被广泛地应用到冶金、煤矿、隧道、建筑等各个领域。但由于注浆过程和机理的复杂性,注浆扩散理论方面的研究相对来说还很不成熟。在工程注浆过程中,注浆量、注浆压力以及浆液的特性参数一般都是根据经验和现场试验[1]等确定,严重地影响了注浆的效果。
近年来,国内外学者在注浆扩散理论方面开展了一些研究,如杨秀竹等[2−3]基于广义达西定律及球形扩散理论模型推导了宾汉浆体和幂律型浆体在岩土中渗透扩散半径的计算公式,分析了浆体性能参数对注浆压力和扩散半径的影响;研究人员研究了沿浆液扩散半径方向上的压力衰减分布规律[4−6];章敏等[7]建立Herschel–Bulkley浆液扩散模型,探讨了注浆时间、注浆压力、流变指数以及裂隙倾角等参数与注浆扩散之间的影响规律;张庆松等[8]基于浆液黏度时空变化的特性,建立了水平裂隙岩体注浆扩散机制;张志沛 等[9]通过FLAC3D软件模拟了软土地基在不同注浆方式和不同注浆压力下浆液在软土地基中的扩散规律;刘健等[10]通过对比模型试验,深入探讨了裂隙注浆扩散机制,系统地研究了浆液在静水和动水中扩散规律。杨志全等[11−13]建立了考虑时变性的宾汉姆流体的流变方程与渗流运动方程,建立了相应的球形及柱形渗透扩散模型;叶飞等[14]基于黏度时变性牛顿流体本构模型,研究了隧道壁后注浆球面渗透扩散规律。这些研究都假定岩土介质孔隙通道是直线的,而在实际工程中,浆液扩散的通道是曲折的。基于孔隙通道线性假设获得的研究结果往往与实际值有明显的偏差,一般情况下对应于同一时刻和同一测点的注浆压力会高于计算得出的压力值。
为了更真实反映岩土介质曲折的孔隙通道,深入揭示浆液的扩散压力和衰减变化规律,本文作者结合分形理论,通过对幂律流体的本构理论进行分析,研究考虑孔隙通道曲折效应条件下幂律流体在多孔介质中的运动规律,重点分析浆体扩散过程中压力的衰减变化规律以及浆体扩散过程中各关键参数的变化规律,为在岩土介质中进行科学合理的注浆设计提供必要的理论依据。
1 考虑孔隙曲折效应的浆液扩散理论模型
图1所示为在恒定注浆压力下浆液在多孔介质中流动示意图,取水平方向为浆液的流动方向,由图1可以看出浆液在孔隙介质中的运动并不都是直线的,还有很多曲折流动通道。

图1 浆液在多孔介质中流动示意图(lt为孔隙通道的实际路线长度;l0为不考虑通道曲折度的表征距离)
为了定量地研究在考虑孔隙通道曲折效应条件下浆液的相关参数,特作以下假定。
1) 浆液是均质的、不可压缩的流体,浆液的密度是常数,且忽略浆液自身的质量。
2) 浆液在扩散过程中无沉淀发生。
1.1 渗流理论分析
多孔介质孔隙通道的曲折度可以由孔隙通道的实际长度t和孔隙通道的表征距离0比值来表示,即:
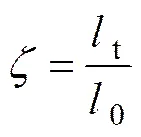
根据修正后的哈根−泊萧叶公式可得,单位时间内通过孔隙截面的浆液流量为
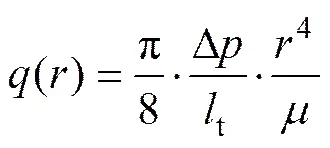
式中:D为截面压力差;为浆液黏度;为孔隙通道半径。
通过一个单元体积的浆液总流量为
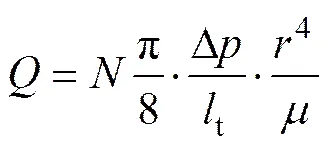
式中:为体积单元中孔隙通道的总数。
由达西定律可得,
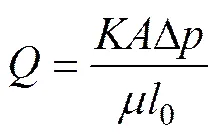
式中:为渗透系数;为截面面积。
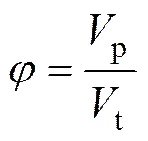
(5-2)

式中:p为孔隙的体积;t为单元总体积。
将式(3)、(4)、(5-1)、(5-2)和(5-3)整体代入式(1),式(1)可进一步表达为
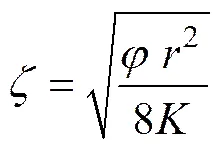
1.2 多孔介质分形理论分析
岩土介质是由一系列孔径大小不同且曲折的孔隙通道和骨架结构组成,根据分形理论,其孔隙通道的曲折程度可表示为

式中:T为孔隙通道曲折度的分维数。
孔隙通道数目与孔隙通道直径的关系可以用分形理论表示[15−16]:
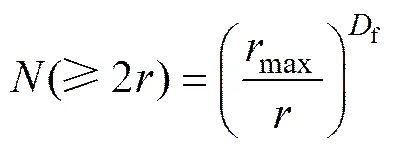
(8-2)
式中:max为孔隙通道最大半径;min为孔隙通道最小半径;f为孔隙通道大小的分形维数。
对式(8-1)求导可得,
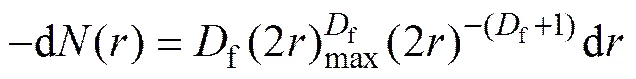
基于分形理论,多孔介质的孔隙度可以表示为
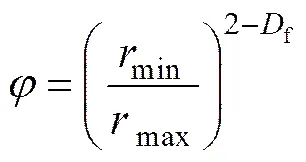
根据式(9)和(10)以及圆柱状面积的定义,通道截面的面积和平均孔隙半径可以表示为
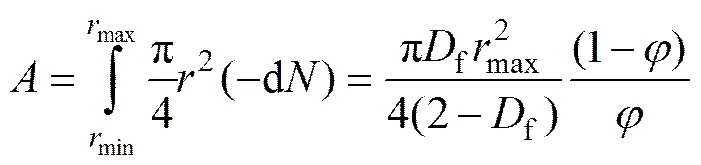
(11-2)
基于分形理论,孔隙通道的曲折度分维数T可以表示为

当表征距离0趋近于无限小时,则截面面积可以近似地认为:

根据文献[15]和公式(10)、(11-1)、(11-2)和(13),长度比率可以进一步表示为
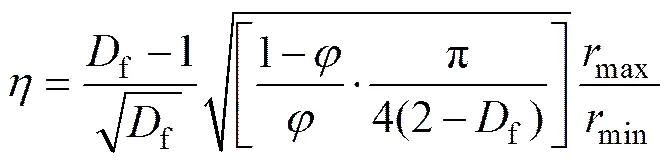
根据分形理论,式(14-1)中的min/max可以表示为

将式(14-1)和(14-2)带入式(12),曲折度分维数可以表示为,
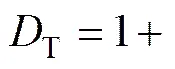
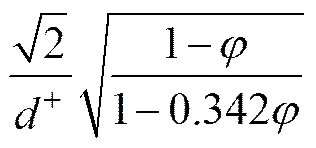
1.3 浆液的渗流运动方程
常见的浆液主要为幂律型流体,其本构方程为

(16-2)
在不考虑其他外力作用下,根据图2和流体在孔隙通道中的受力平衡关系可得:
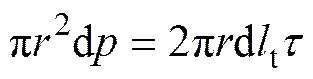
(17-2)

图2 幂律型浆液在孔隙通道中的流动示意图
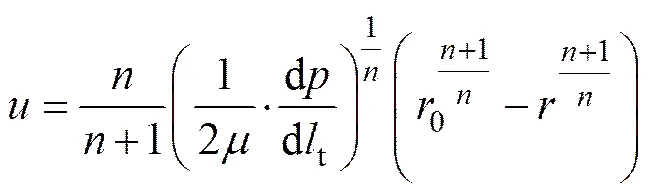
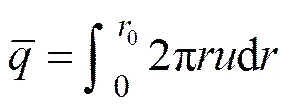
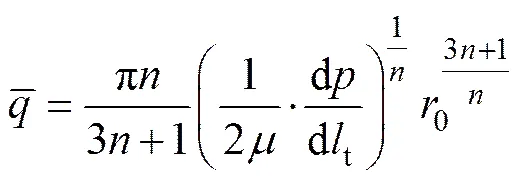
根据单位时间内注入孔隙的浆液量与扩散半径增大所需的浆液量相等,从而可以得出时间内的注浆量,

式中:为注浆时间。
对式(21)进行积分可得,

将式(20)代入式(21),并结合式(22),可得,
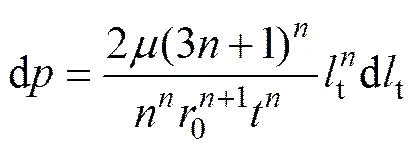
在(0,t)范围内,对式(23)进行积分;当边界条件为t=0时,,浆液扩散规律方程可以表示为
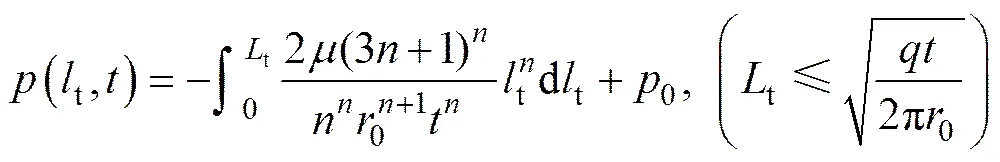
由式(7)、式(15)和式(23),可以得到基于扩散通道曲折效应的浆液扩散方程:
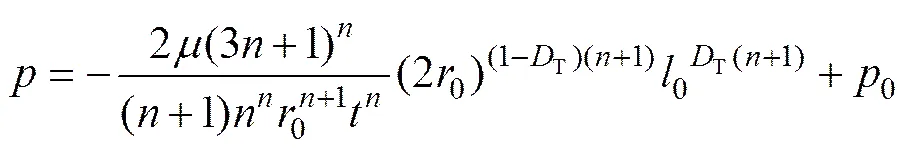
根据式(22)和式(25),注浆压力变化规律可以进一步表示为

2 考虑孔隙曲折效应的浆液扩散压力变化规律
下面基于以上模型分析考虑孔隙曲折效应时浆液的扩散压力与各特征参数的关系。
2.1 不同扩散距离时注浆压力降变化规律
图3所示为注浆扩散压力随浆液扩散距离的变化规律,可见,注浆扩散压力随着扩散距离的增大是非线性衰减的,这一结论在理论和实验上都得到了证 实[17−18]。若不考虑孔隙通道的曲折效应,在其他条件相同的情况下,注浆浆液扩散压力缓慢衰减,如图3中方框节点曲线所示;当考虑孔隙通道曲折度时,扩散压力随扩散距离的增大呈现急剧下降趋势,如图3中十字节点曲线所示。考虑孔隙通道曲折效应时,其扩散初始阶段注浆压力衰减程度比不考虑曲折效应条件下相差很大,这可能是由于考虑曲折效应时,浆液在孔隙通道流通时,不仅需要克服浆液内部的剪切力和孔隙通道壁的吸附黏滞阻力,同时也会受到孔隙通道壁面的正面碰撞阻力,这会使注浆压力在扩散过程中的损耗迅速增加。
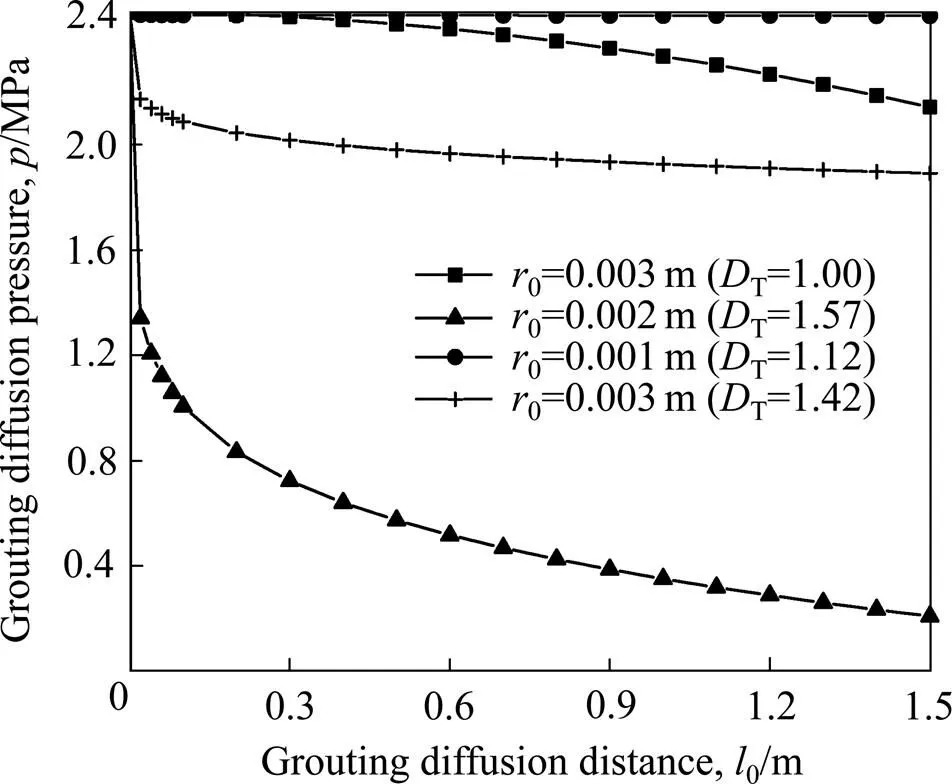
图3 注浆扩散压力随浆液扩散距离的变化规律(q=1 m3/s,n=0.9,m=0.02 Pa·sn,K=0.3,f=0.5)
2.2 浆体黏度对注浆压力降的影响规律
黏度对浆液在扩散过程的压力衰减影响规律如图4所示。可见,浆液的黏度越大,到达相同的扩散距离所需的注浆压力损耗也越大。这可以理解为,浆液的黏度越大,发生流动所需克服的剪切变形阻力越大,因此注浆过程中损失压力能耗也越大,在相同条件下,浆液扩散到相同距离所对应的压力“剩余值”就越小。同时由图4还可得到,考虑孔隙曲折效应情况下,其压力衰减的程度较为急剧,这是由于浆液在多孔介质中扩散时,不仅受到自身剪切力的影响,同时还受到浆液与孔隙通道壁面的黏滞力作用;而黏滞力不仅与浆液的黏度有关,而且与浆液和孔壁之间的接触表面积有关,当考虑孔隙通道的曲折效应时,浆液流通的实际距离往往比表征距离大,从而使得浆液与孔壁的接触面积变大,所以相对于不考虑曲折效应的情况,其压力衰减幅值更大。
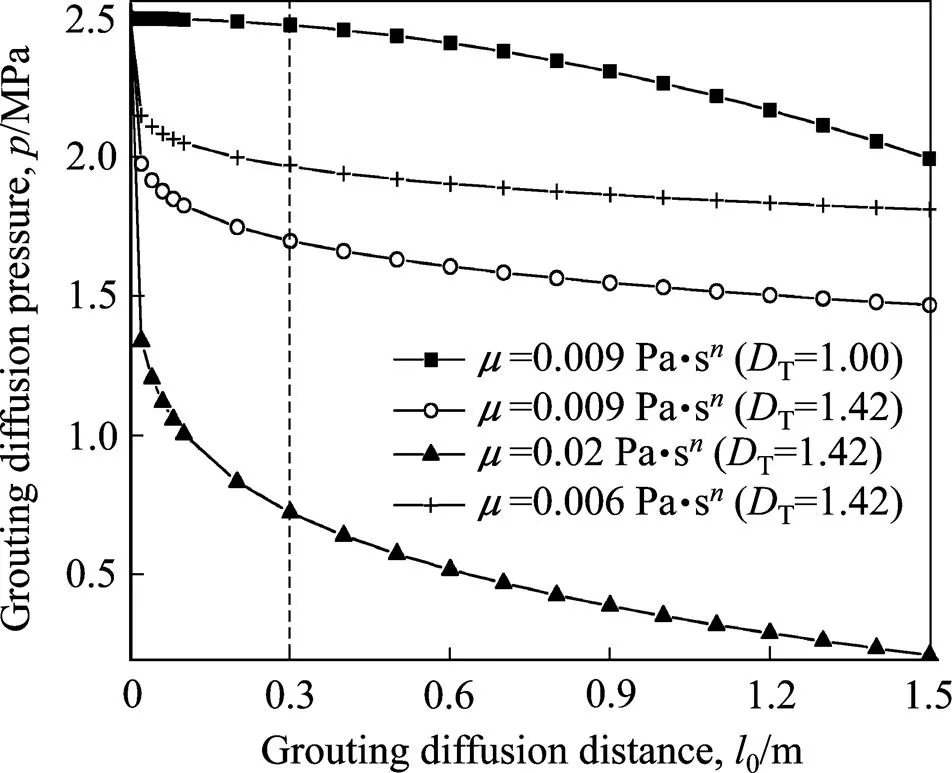
图4 黏度对注浆压力降的影响规律(q=1 m3/s,n=0.9,r0=0.003 m,K=0.3,f=0.5)
2.3 流变指数对注浆压力降的影响规律
图5所示为注浆压力损耗随流变指数的变化曲线,可见,流变指数在0.1~0.6之间时,注浆压力损耗随着流变指数的增大呈现非线性减小,当流变指数超过0.6以后,注浆压力损耗值变化较小。若不考虑曲折效应,在相同的条件下,其压力损耗衰减趋势较缓,如图5中方框节点曲线所示;若考虑曲折效应,其压力损耗随流变指数的增大呈现急剧下降趋势,之后变化幅度很小,如图5中实心圆节点曲线所示。当流变指数越接近1,流体的性质越接近牛顿流体,其流动性较好,此时随着流变指数的不断增大,浆液的表观黏度相对来说也会变小,产生的流动阻力也较小,要使浆体流动只需要克服较小的流动阻力做功即可,因此注浆压力损耗在整体上会随着流变指数的增大而减小。
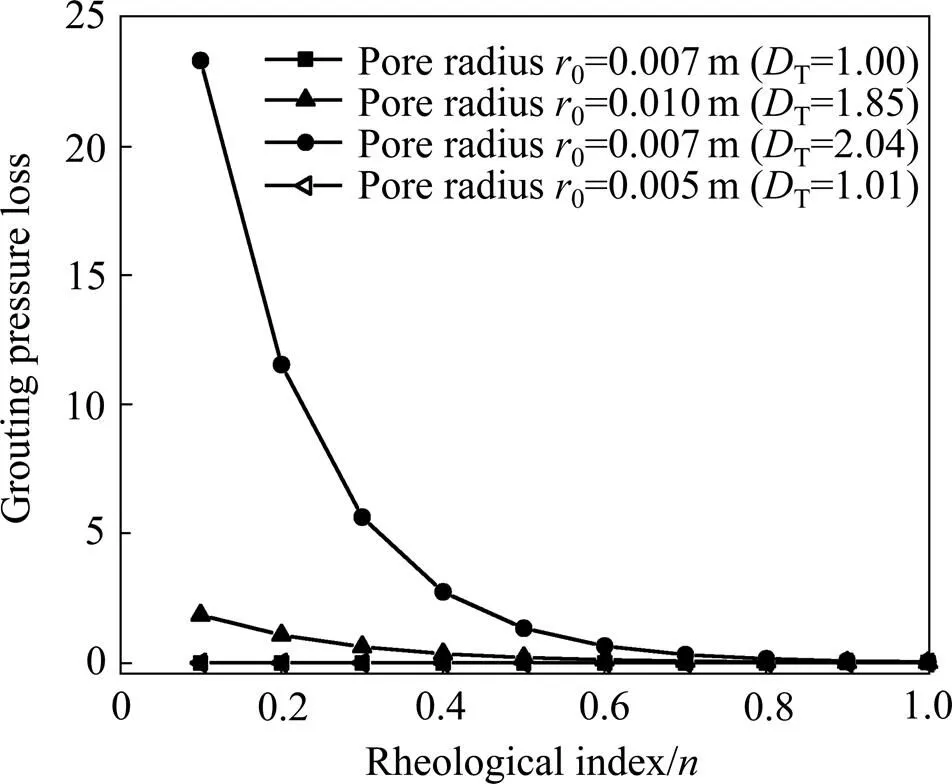
图5 注浆压力损耗随流变指数的变化曲线(q=1 m3/s,m=0.02 Pa·sn,K=0.3,f=0.5,l0=0.5 m)
2.4 注浆压力降与单位注浆量的影响规律
图6所示为注浆压力差随单位注浆量的变化规律曲线,可见,注浆压力差总体上随着单位注浆量的增大而增加。若不考虑曲折效应,在其他条件相同的情况下,其注浆压力差随着单位注浆量的增加变化不大,如图6中方框节点曲线所示;考虑曲折效应时,注浆压力差随单位注浆量的增大呈现非线性急剧增加后缓慢增加的趋势,如图6中十字节点曲线所示。由此可以看出考虑曲折效应情况下的注浆压力差值明显大于不考虑曲折效应的结果,因此利用不考虑曲析效应的注浆理论对工程进行设计会带来很大的误差。
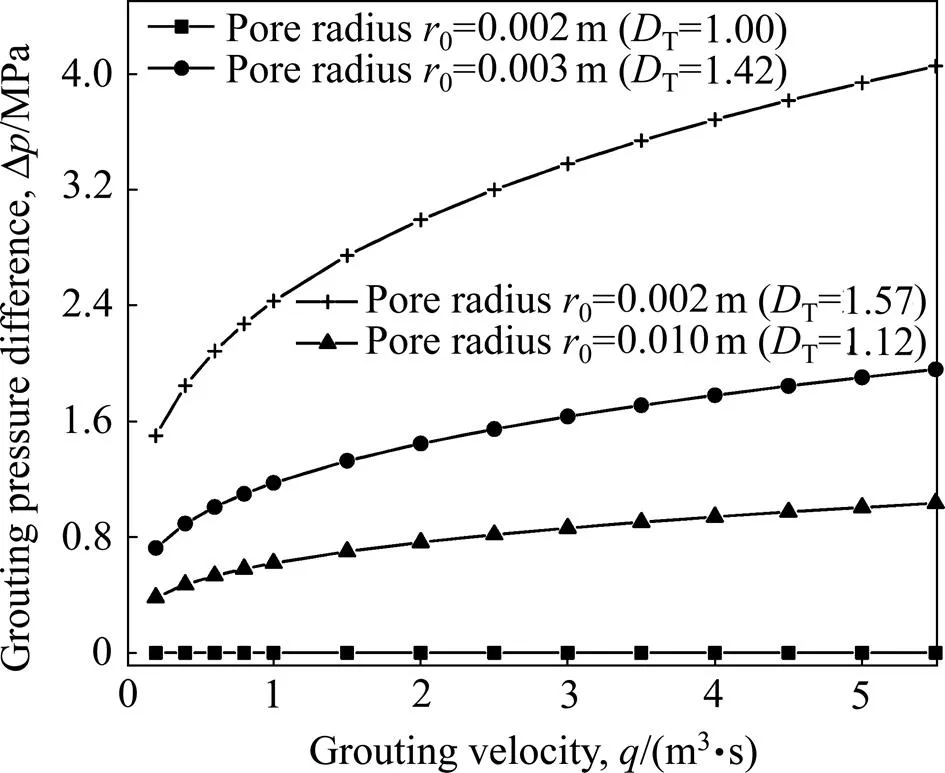
图6 注浆压力差随单位注浆量的变化规律曲线(n=0.9,m=0.02 Pa·sn,K=0.3,f=0.5,l0=0.5 m)
3 结论
1) 基于分形理论和幂律流体本构理论,建立了考虑岩土介质孔隙通道曲折效应的浆液扩散理论模型,探讨了浆液黏度、流变指数、单位注浆量对注浆压力差的影响规律。
2) 与不考虑孔隙曲折效应的模型对比,本模型所得的结果表明孔隙曲折效应对浆液扩散有显著影响。若不考虑曲折效应,在其他条件相同的情况下,其注浆压力随扩散距离的增大而缓慢衰减,若采用本研究所推导的模型,其注浆压力随扩散距离的增大呈现急剧下降趋势。由此可见,若不考虑孔隙通道的曲折效应,会给工程实践参数的选取带来较大的误差。
3) 相比较以往的研究,该模型较合理地揭示了浆液在多孔介质中的扩散规律,使得浆液的模拟环境和实际环境差异变小,在一定程度上可为注浆工艺参数的设计提供依据。
REFERENCES
[1] 杨 坪, 唐益群, 彭振斌, 陈 安. 砂卵(砾)石层中注浆模拟试验研究[J]. 岩土工程学报, 2006, 28(12): 2134−2138. YANG Ping, TANG Yi-qun, PENG Zhen-bin, CHEN An. Study on grouting simulating experiment in sandy gravels[J].Chinese Journal of Geotechnical Engineering, 2006, 28(12): 2134−2138.
[2] 杨秀竹, 王星华, 雷金山. 宾汉体浆液扩散半径的研究及应用[J]. 水利学报, 2004(6): 75−79. YANG Xiu-zhu, WANG Xing-hua, LEI Jin-shan. Study on grouting diffusion radius of Bingham fluids[J]. Journal of Hydraulic Engineering, 2004(6): 75−79.
[3] 杨秀竹, 雷金山, 夏力农, 王星华. 幂律型浆液扩散半径研究[J]. 岩土力学, 2005, 26(11): 112−115. YANG Xiu-zhu, LEI Jin-shan, XIA Li-nong, WANG Xing-hua. Study on grouting diffusion radius of exponential fluids[J]. Rock and Soil Mechanics, 2005, 26(11): 112−115.
[4] 邹金锋, 李 亮, 杨小礼. 劈裂注浆扩散半径及压力衰减分析[J]. 水利学报, 2006, 37(3): 314−319. ZOU Jin-feng, LI Liang, YANG Xiao-li. Penetration radius and pressure attenuation law in fracturing grouting[J]. Journal of Hydraulic Engineering, 2006, 37(3): 314−319.
[5] 张 淼, 邹金锋, 陈嘉祺, 李 亮, 李振存. 非对称荷载作用下土体劈裂注浆压力分析[J]. 岩土力学, 2013, 34(8): 2255−2263. ZHANG Miao, ZOU Jin-feng, CHEN Jia-qi, LI Liang, LI Zhen-cun. Analysis of soil fracturing grouting pressure under asymmetric loads[J]. Rock and Soil Mechanics, 2013, 34(8): 2255−2263.
[6] KELESSIDIS V C, DALAMARINIS P, MAGLIONE R. Experimental study and predictions of pressure losses of fluids modeled as Herschel–Bulkley in concentric and eccentric annuli in laminar, transitional and turbulent flows[J]. Journal of Petroleum Science and Engineering, 2011, 77(3): 305−312.
[7] 章 敏, 王星华, 汪 优. Herschel–Bulkley浆液在裂隙中的扩散规律研究[J]. 岩土工程学报, 2011, 33(5): 815−820. ZHANG Min, WANG Xing-hua, WANG You. Diffusion of Herschel–Bulkley slurry in fractures[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(5): 815−820.
[8] 张庆松, 张连震, 张 霄, 刘人太, 朱明听, 郑东柱. 基于浆液黏度时空变化的水平裂隙岩体注浆扩散机制[J]. 岩石力学与工程学报, 2015, 34(6): 1198−1210. ZHANG Qing-song, ZHANG Lian-zhen, ZHANG Xiao, LIU Ren-tai, ZHU Ming-ting, ZHENG Dong-zhu. Grouting diffusion in a horizontal crack considering temporal and spatial variation of viscosity[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1198−1210.
[9] 张志沛, 彭 惠, 饶 晓. 软土地基注浆扩散过程数值模拟研究[J]. 岩土力学, 2011, 32(S1): 652−655. ZHANG Zhi-pei, PENG Hui, RAO Xiao. Numerical simulation study of grouting diffusion process in soft soil foundation[J]. Rock and Soil Mechanics, 2011, 32(S1): 652−655.
[10] 刘 健, 刘人太, 张 霄, 李术才. 水泥浆液裂隙注浆扩散规律模型试验与数值模拟[J]. 岩石力学与工程学报, 2012, 31(12): 2445−2452. LIU Jian, LIU Rentai, ZHANG Xiao, LI Su-cai. Diffusion law model test and numerical simulation of cement fracture grouting[J].Chinese Journal of Rock Mechanics and Engineering, 2012, 31(12): 2445−2452.
[11] 杨志全, 侯克鹏, 程 涌, 杨八九. 幂律型流体的柱-半球形渗透注浆机制研究[J]. 岩石力学与工程学报, 2014, 33(S2): 3840−3846. YANG Zhi-quan, HOU Ke-peng, CHENG Yong, YANG Ba-jiu. Study of column-hemispherical penetration grouting mechanism based on power-law fluid[J]. Chinese Journal of Rock Mechanics and Engineering, 2014, 33(S2): 3840−3846.
[12] 杨志全, 牛向东, 侯克鹏, 周宗红, 梁 维, 郭延辉, 芦涌峰, 杨八九, 程 涌. 流变参数时变性幂律型水泥浆液的柱形渗透注浆机制研究[J]. 岩石力学与工程学报, 2015, 34(7): 1415−1425. YANG Zhi-quan, NIU Xiang-dong, HOU Ke-peng, ZHOU Zong-hong, LIANG Wei, GUO Yan-hui, LU Yong-feng, YANG Ba-jiu, CHENG Yong. Columnar diffusion of cement grout with time dependent rheological parameters[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(7): 1415−1425.
[13] 杨志全, 侯克鹏, 郭婷婷, 马 秋. 黏度时变性宾汉体浆液的柱−半球形渗透注浆机制研究[J]. 岩土力学, 2011, 32(9): 2697−2703. YANG Zhi-quan, HOU Ke-peng, GUO Ting-ting, MA Qiu. Study of column-hemispherical penetration grouting mechanism based on Bingham fluid of time-dependent behavior of viscosity[J]. Rock and Soil Mechanics, 2011, 32(9): 2697−2703.
[14] 叶 飞, 朱合华, 何 川. 盾构隧道壁后注浆扩散模式及对管片的压力分析[J]. 岩土力学, 2009, 30(5): 1307−1312. YE Fei1, ZHU He-hua, HE Chuan. Back-filled grouts diffusion model and its pressure to segments of shield tunnel[J]. Rock and Soil Mechanics, 2009, 30(5): 1307−1312.
[15] YU Bo-ming. Fractal character for tortuous streamtubes in porous media[J]. Chinese Physics Letters, 2005, 22(1): 158−160.
[16] XU Peng, YU Bo-ming. Developing a new form of permeability and Kozeny-Carman constant for homogeneous porous media by means of fractal geometry[J]. Advances in Water Resources, 2008, 31(1): 74−81.
[17] 杜新龙. 低渗透砂岩油层微流动机理研究[D]. 成都: 西南石油大学, 2012. DU Xin-long. Mechanism of micro flow in low-permeability sandstone reservoirs[D]. Chengdu: Southwest Petroleum University, 2012.
[18] 李学文. 乳状液在孔隙介质中渗流规律的研究[D]. 大庆: 大庆石油学院, 2004. LI Xue-wen. The study on f1owing rules of emulsion through porous medium[D]. Daqing: Daqing Petroleum Institute, 2004.
Grout dispersion considering effect of pore tortuosity
ZHOU Zi-long1, DU Xue-ming1, CHEN Zhao2, ZHAO Yun-long1, CHEN Lu1
(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China; 2. Guangxi Xianglu Construction Co.LTD., Nanning 530029, China)
The pore channel of porous media is tortuous in practice, however, the tortuosity of the pore channel of the injected medium is ignored in the traditional method, which results in obvious bias between the calculated value and the actual value of grouting pressure. The tortuosity equation of the pore channel was derived according to the fractal theory. A slurry diffusion model considering the effect of tortuosity of the pore channel was derived based on the above equation and the constitutive equation of the power law fluid. The effect of pore tortuosity on diffusion pressure were analyzed with the new model. And the change laws of slurry viscosity, rheological index and the unit volume of grouting on the attenuation of grouting pressure were also discussed. The results shows that without taking pore tortuosity into account, the grouting pressure presents the trend of slow attenuation with the increase of the diffusion distance. However, by using the deduced model considering the pore tortuosity, the grouting pressure presents the trend of sharp downward with the increase of the diffusion distance. And the pressure loss decreases rapidly with the increase of the rheological index in a certain range, and then the change range is very small.
pore tortuosity; fractal theory; grouting pressure; diffusion law
Project(2015CB060200) supported by the National Basic Research Program of China;Project (51322403) supported by the National Natural Science Outstanding Youths Foundation of China; Project(2015CX005, 2016CX017) supported by Innovation Plan of CSU, China;Project (2016zzts093) supported by the Fundamental Research Funds for the Central Universities of Central South University
2016-01-20; Accepted date:2016-06-20
ZHOU Zi-long; Tel: +86-13787202629; E-mail: zlzhou@mail.csu.edu.cn
1004-0609(2016)-08-1721-07
TV139.14
A
国家重点基础研究发展计划资助项目(2015CB060200);国家自然科学优秀青年基金资助项目(51322403);中南大学创新驱动资助项目(2015cx005,2016CX017);中南大学中央高校基本科研业务费专用资金资助项目(2016zzts093)
2016-01-20;
2016-06-20
周子龙,教授,博士;电话:13787202629;E-mail: zlzhou@mail.csu.edu.cn
(编辑 王 超)
