民用飞机安全性分析中单点失效MTBF的算法
2016-10-24赵长啸
杨 可,赵长啸
(中国民航大学 a.工程技术训练中心;b.适航审定研究中心,天津 300300)
民用飞机安全性分析中单点失效MTBF的算法
杨可a,赵长啸b
(中国民航大学 a.工程技术训练中心;b.适航审定研究中心,天津300300)
安全是民航工业的生命线。按照适航规章要求,任何妨碍飞机继续安全飞行与着陆的单点失效的出现是极不可能的。传统的参数,如平均故障间隔时间(MTBF),是用来计算部件失效概率的常用参数,但由于关键安全部件可能在平均故障间隔时间之前出现故障,因此,该参数的传统计算方法对于单点失效概率的分析并不适用。提出评价单点失效概率的分析方法,即基于所给出数据样本量的大小,提出了评价单点失效概率的计算公式。给出了两个案例来进一步验证所提方法的有效性。
单点失效;MTBF;概率;安全性评估
旅客信任航空业的基础是安全,要求其产品及运行无事故[1]。安全分析是飞机安全性设计的关键组成部分。通常安全分析由未参与飞机设计过程的工程师通过常用的定性方法(如FMEA,失效模式及影响度分析)与定量方法(如FTA,故障树分析)相结合而展开分析[2]。
单点失效分析通常采用“自底向上”的分析方法[3],如FMEA。但当失效影响为“隐性”时,现有假设“失效的可能组合”仅考虑了单点隐性失效与“下一个最坏的”失效相结合,这种分析方式适用于简单机械、液压机械或电力系统的评价,然而,随着设计中功能的融合和多样化以及技术的增加,尤其设计中包含了数字航空电子设备,其结果导致了复杂性、相互依赖性的增加,原有假设飞机中失效影响的独立性已不成立,同时零部件计数法使得“隐性—下一个最坏”失效关于“失效概率结合”的假设尚有置疑。因此,为了确保对于大量存在的失效,设计是“失效—安全”的,通常需要利用概率方法。
除了传统的方法,如故障树(FTA)[4]、关联图(DD)[5],许多安全评价的方法已在航空业运用。例如,达索7x飞行控制系统通过AltaRica语言建立数据流模型以证明安全性[6]。由ESACS及ISAAC项目提出的扩展系统模型(ESM)/失效注入模型(FI)方法介绍了航空领域基于模型的安全评价(MBSA)[7]。国内学者利用BBD方法分析了基于任务的航空电子网络可靠性[8]。
以上研究都试图解决复杂系统的安全/可靠性评价问题,并未太多关注于单点失效的概率分析。许多工程师认为,由于安全关键部件可能会在平均故障间隔时间(MTBF)前失效,因此单点失效利用传统MTBF进行计算分析不再满足系统安全性需求。
本文提出了如何利用可靠性数据MTBF来计算单点失效概率的方法,同时就大样本量数据及小样本量数据分别提出了两个计算公式。基于工业中常用的风险管理原则,这两个公式的置信水平均为95%。同时,提出两个案例以验证所提方法的有效性。
1 问题描述
1.1单点失效的安全要求
单点失效作为系统的一部分,一旦发生将导致整个系统停止工作。在民航领域,要求任何灾难性失效状态不会由单点失效导致。因此必须建立故障分析、部件测试或仿真环境测试,验证没有单点失效或其可能的失效结合会妨碍飞机的安全运行。适航规章FAA25.1309指出[9],飞机系统及相关部件的设计,要单独考虑且与其他系统一同考虑,使得灾难性失效状态的概率极为不可能且不是由单点失效导致。同时,要求任何危险性失效状态概率为极微小的,任何重大失效状态概率为微小的。
1.2单点失效出现的概率
适航要求指出,不允许由任何单点失效造成灾难性失效状态。但对于能造成并非特别严重的失效状态如危险失效状态的单点失效,则必须进行考虑。问题在于如何评价“单点失效”的概率以满足功能危险性分析(FHA)的安全目标。许多工程师认为由于安全关键部件可能会在平均故障间隔(MTBF)[10]之前失效,所以MTBF不再被使用,因此需给出关于关键单点失效概率的评价方法。
当对一个给定的失效状态进行概率预测时,故障率影响的方差将会导致多重失效因素相互抵消。因此,使用部件的平均可靠性(如MTBF)进行计算是合理的,然而这并没有考虑单点失效的情况。接受单点失效的一个重要条件,就是要考虑主要部件可靠性预测概率的“最小值”在控制范围内,且在失效状态概率分配中不占主导地位。也就是说,单点失效的“最小”时间间隔应该比最可能的多重失效情况的“平均”时间间隔更长。在下文中将介绍一种新的单点失效概率的预测方法。
2 单点失效概率的预测方法
2.1预测方法
如果单点失效存在,必须要有足够的置信水平(通常是95%),以确保单点失效的间隔时间比很可能发生的多重失效的间隔时间长[11]。换言之,令单点失效部件的MTBF等于T,如果该部件95%置信区间内的无故障时间间隔为T0,且T0>T,则此部件满足安全需求。这个过程可由概率及统计理论推导。
以部件YK-75为例来解释这种方法。部件YK-75单点失效会造成危险的失效状态FC-T-1,如图1所示。此案例中平均飞行小时数T0为1 h。

图1 FC-T-1故障树Fig.1 FC-T-1 fault tree
根据AC25.1309-1B(草案)及SAEARP 4761[12],如果部件的失效分布函数服从指数分布,则1/MTBF= λ,进而展开概率计算。
根据统计理论,由供应商提供的YK-75部件的寿命服从正态分布,MTBF为部件最有可能的寿命。然而,很明显对于每一个部件不可能有完全相同的寿命MTBF,也就是说几乎有一半的部件寿命小于MTBF。换言之,如果将YK-75的MTBF作为基础计算数据,系统将有50%的可能承担“低于预期的安全”的风险。
假设YK-75为安全关键部件,其发生将导致顶事件失效状态的发生,直接使用MTBF计算单点失效概率则无可行性。MTBFSF作为决定性参数,可代替MTBF来评价安全目标是否得到满足,这意味着需要更高的可靠性水平。
这里的“MTBFSF”(SF为单点失效)代表修正过的MTBF计算表达符号,可直接用于单点失效概率的计算,其表达式为

上式表明,MTBFSF是MTBF的函数。如果这种失效可与其他失效相结合导致顶事件的发生,则可直接使用MTBF计算。但如果这种失效为单点失效,则在故障树分析中应该使用MTBFSF进行计算。
图1中故障树的顶事件失效状态FC-T-1平均每飞行小时概率计算为
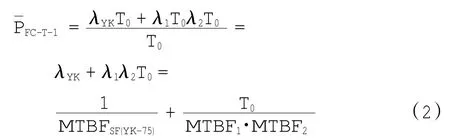
其中:MTBFSF(YK-75)为单点失效概率,根据式(1),由供应商提供的YK-75的MTBF常量计算得到;MTBF1与MTBF2为供应商提供的常量。因为二者是组合失效中的元素,因此这些数据可被直接使用。
考虑到工业实践经验及可靠性数据的样本量,在此给出两种方法将供应商提供的常量MTBF转换为MTBFSF,运用以下两个公式很容易得到高置信度的MTBFSF的值,以计算单点失效的概率。
2.2基于大样本量的MTBF转换公式
由供应商AB生产的一大批部件XY,其寿命服从正态分布X~N(μ1,σ2),整个统计分析包含n个样本(即样本变量)为μ1的无偏估计量,S2为σ2的无偏估计量,即
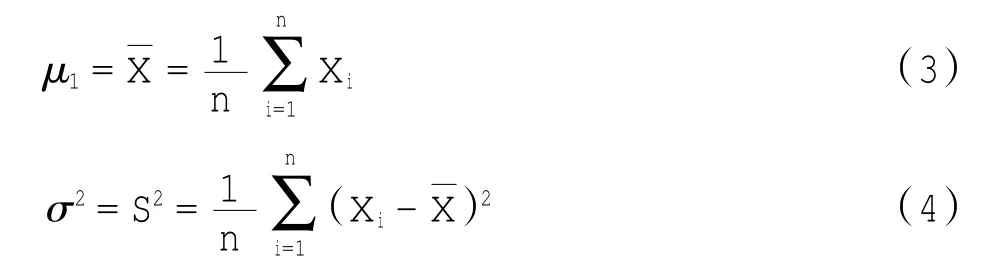
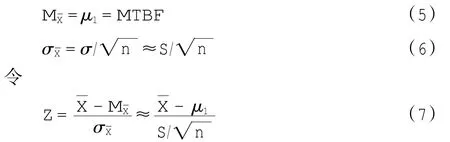
根据分布特征,如果n足够大,则t分布可近似看作标准正态分布N(0,1),从t分布表中可知,当n> 45时,可以使用正态分布;当n<45时,仍必须使用t分布进行计算。现假设n>45,则以下均为近似值。
图2显示了Z的概率密度。
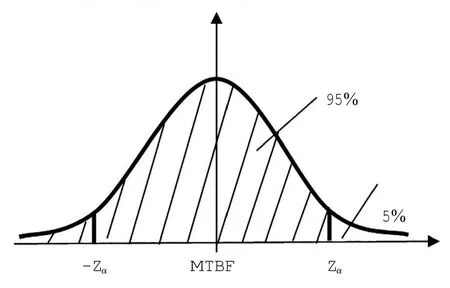
图2 置信水平分析Fig.2 Confidence level analysis
找到Zα分位点,令Z≤Zα的概率处于95%的高置信水平,阴影面积代表Z≤Zα的概率,则图2可进一步表示为
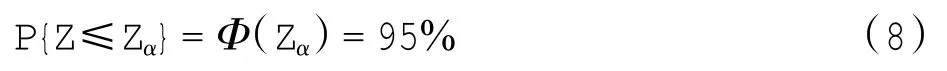
根据标准正态分布得Zα=1.65,于是
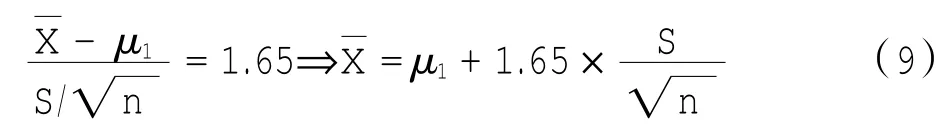
因此,在95%的置信度下
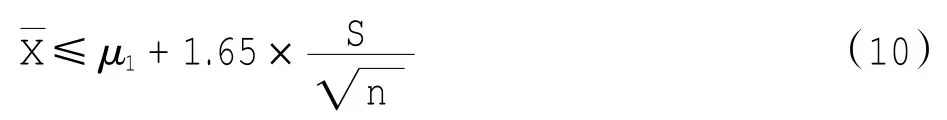
部件XY经参数转换后的高置信度MTBFSF可根据图3计算
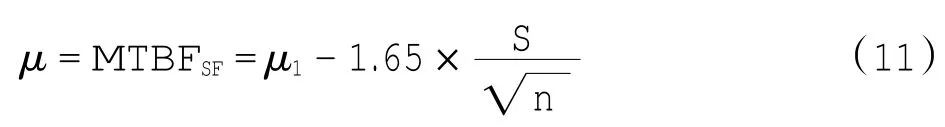
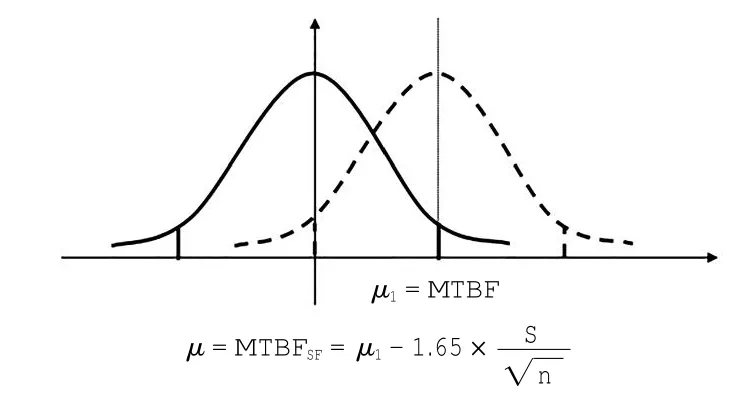
图3 MTBF与MTBFSF的关系Fig.3 Relationship between MTBF and MTBFSF
实线为高置信度的MTBFSF,虚线为样本分布。均值μ1为供应商提供的MTBF。因此,高置信度的MTBFSF比MTBF计算单点失效更易接受。
95%的置信度可保证部件XY的MTBF满足安全目标,且此置信水平也可满足安全需求。因此,如果部件XY满足此目标,就可保证“单点失效可控并能保持系统安全水平”。
大样本数据的计算公式为
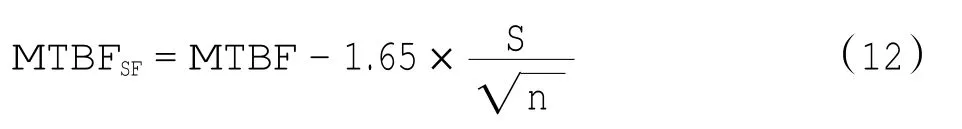
其中:MTBFSF用于直接计算单点失效概率;MTBF是供应商可靠性数据库中的统计量;S为样本标准方差;n为样本量。
2.3基于小样本量的MTBF转换公式
上文已介绍了计算大样本量的可靠性数据置信区间的方法,然而,通常实际中单点失效发生率很低,统计样本量n非常有限,如果n很小,则会导致样本标准错误很大,这种情况下用这种方法进行数据计算并不适用。因此,以下将给出另一种方法来计算在给定的置信水平内小概率事件的置信区间。
通常飞机故障,失效或缺陷往往是在实际服务中才能观察到的问题。用于概率计算的数据即观察到的事件数量、航班数量或飞行暴露时间。假设小概率事件发生的可能性可以近似通过划分事件的数量、飞行小时数得到,则概率等于观察到的事件率。因此,概率计算简单地基于观察到事件的数量、飞行小时数以及飞行暴露。例如,如果在450 000个飞行小时内观察到9起燃油泄漏事件,则事件的平均每飞行小时概率为9/450 000=2E-5。注意这个简单的计算提供了一个单点概率,此值用于平均每飞行小时的概率,而不考虑产品寿命。因此,假设失效的概率仍然保持不变,如产品寿命。
当概率计算必须基于观察到的少量事件时,结果就会受到显著的统计不确定性影响。因此,在风险分析假设中,通过采用比分析更有效的风险降低计划或通过增加分析结果的置信范围以提高结果的保守性。以下公式适用于独立于产品寿命的事件概率,统计假设观察到的事件服从于泊松分布


根据前例,在450 000飞行小时内观察到的9起燃油泄漏事件在90%的置信度下可通过以下参数值计算:T=450 000 h,α=1-0.9=0.1,r=9。根据χ2分布表,得

带入式(13)可得

3.157E-5为保守概率的上限,此上限提供了一个调整后的不确定性统计的概率值近似。调整量为样本量(如9起事件)及选定的置信水平(如90%)的函数。对于在450 000飞行小时中发生的9起燃油泄漏事件,落入90%置信范围的概率与通过观察得到的“置信因素”的概率之比为1.578。
对于单点失效(λ=P/T)而言,由于P是平均每飞行小时的概率(T=1 h),因此事件的MTBF接近于

MTBF90%的置信区间为
31 496 换言之,有95%的可能使MTBF的值超过31496h。 假设燃油泄漏事件是一个单点失效,MTBF的安全需求为μ,如果μ≤31 496,则至少有95%的概率可以保证MTBF的值大于安全目标,这也就意味着单点失效可以满足安全需求。换言之,当单点失效的概率很小时,由供应商提供的可用于可靠性统计的样本数据很小,MTBF仅可以从很少量的样本观察事件中获得,因此式(14)为小样本数据的函数 3.1大样本公式的应用 表1中可靠性数据来源于中国某航空公司的可靠性数据中心。 表1 部件XX-1的可靠性数据Tab.1 Reliability data of component XX-1 表1中样本量为65,第5列为每个部件的失效时间(min),除以60可换算为小时。 利用式(1)计算置信水平为90%的置信区间: 样本均值为 样本标准差为 其中:样本量n=65;置信水平α=1-0.9=0.1;常用的MTBF=4745 h。 如果计算单点失效概率,应采用式(12)计算 3.2小样本公式的应用(近似小概率事件) 表2中的可靠性数据来源于中国某航空公司的可靠性数据中心。 表2 部件XX-2的可靠性数据Tab.2 Reliability data of component XX-2 表2中的样本量为5,第5列为每个部件的失效时间。 利用2.3中提到的方法计算在90%的置信水平下部件的置信区间。利用等式 得出90%置信水平的下限为 通过近似计算,部件MTBF90%的置信区间为 假设部件失效为单点失效,利用式(14),常用的MTBF=2.5E+7 h。 计算单点失效概率,则应采用以下数值 如果计算关键单点失效的概率,在不考虑附加条件的情况下,不能使用平均可靠性数据MTBF。由于导致单点失效的时间间隔应大于导致多重失效的平均时间间隔,因此MTBF不适用于单点失效。 本文提出了评价单点失效概率的方法,分别给出了基于大样本数据以及小样本数据的两个概率计算公式。基于风险管理原则,这两个公式都具有95%的置信水平。最后,分析了两个真实的案例以验证所提方法的有效性。 [1]HEWITT J,PHAM J.Quantitative Risk Assessment Enhances Customer TrustinAviation[C]//ReliabilityandMaintainabilitySymposium(RAMS), 2014 Annual.IEEE,2014:1-6. [2]ZHU Y,ZHANG J,GONG Q,et al.Reliability and Safety Assessment with AltaRica for Complex Aircraft Systems[C]//Reliability,Maintainability and Safety(ICRMS),2011 9th International Conference on.IEEE, 2011:588-593. [3]YANG J,HUANG H Z,HE L P,et al.Risk evaluation in failure mode and effects analysis of aircraft turbine rotor blades using Dempster-Shafer evidence theory under uncertainty[J].Engineering Failure Analysis,2011,18(8):2084-2092. [4]LIU C B.Aircraft Fuel Tank System Fire Disaster Analysis based on FMEA and FTA[C]//QR2MSE 2013,IEEE Computer Society,IEEE, 2013. [5]MYERS ALBERT,RAUZY ANTOINE.Efficient reliability assessment of redundant systems subject to imperfect fault coverage using binary decision diagrams[J].IEEE Transactions on Reliability,2008,57(2): 336-348. [6]ÅKERLUND O,BIEBER P,BÖEDE E,et al.ISAAC,a Framework for Integrated Safety Analysis of Functional[C]//Geometrical and Human Aspects,in 3rd European Congress on Embedded Real Time Systems (ERTS).Toulouse,France,2006. [7]LISAGOR O.A Pragmatic Approach[D].York:The University of York, 2010. [8]ZHAO C X,CHEN Y,WANG H L,et al.Reliability analysis of aircraft condition monitoring network using an enhanced BDD algorithm[J].Chinese Journal of Aeronautics,2012,25(6):925-930. [9]FAA.Arsenal Version of AC1309(draft),System Design and Analysis [S].America:Federal Aviation Administration,2002. [10]YUN W Y,PARK GOEUN,HAN Y J.An optimal reliability and maintainability design of a searching system[J].CommunicationsinStatistics:Simulation and Computation,2014,43(8):1959-1978. [11]ZANIN M.Network analysis reveals patterns behind air safety events[J]. Physica A:Statistical Mechanics and its Applications,2014,401:201-206. [12]SAE.APR4761,Guidelines and Methods for Conducting the Safety Assessment Process on Civil Airborne Systems and Equipments[S].America:The Engineering Society For Advancing Mobility Land Sea Air and Space,1996. (责任编辑:杨媛媛) Single failure MTBF analysis on aircraft safety assessment YANG Kea,ZHAO Changxiaob Safety is the lifeline of civil aviation industry.The regulations proposed by airworthiness authorities require that the occurrence of any single failure which would prevent continuous safe flight and landing of airplanes is extremely improbable.While the ambiguous description makes it difficult to calculate the occurrence of single failure in practice.The traditional parameter,mean time between failure(MTBF),is not suitable for single failure analysis due to the possibility that critical safety components may fail before MTBF.A method is proposed to evaluate the probability of single failure.The evaluating formula for the occurrence probability of single failure basing on sample size is given.Practical cases are used to verify the effectiveness of this method. single failure;MTBF;probability;safety assessment V240.2 A 1674-5590(2016)04-0011-05 2016-01-13; 2016-04-05基金项目:国家自然科学基金项目(U1533105) 杨可(1985-),女,湖北宜城人,助教,硕士,研究方向为民用航空器维修、系统安全性分析.
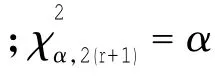
3 实验

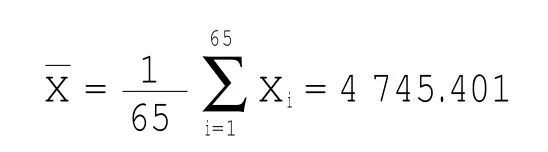

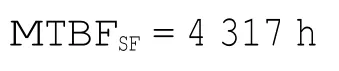
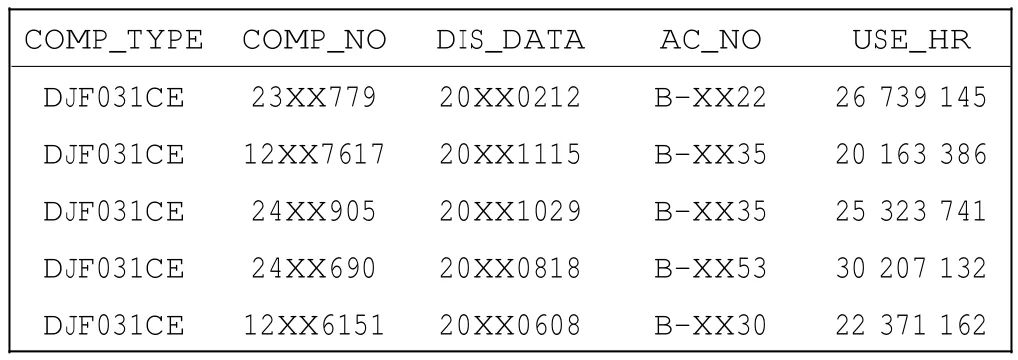


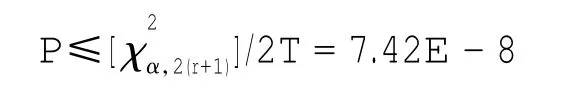
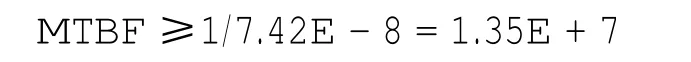


4 结语
(a.Engineering Techniques Training Center;b.Airworthiness Certification Technology Research&Management Center,CAUC,Tianjin 300300,China)
