北京首都机场畅通滑行时间研究

赵嶷飞，唐华龙

（中国民航大学空中交通管理研究基地，天津　300300）

北京首都机场畅通滑行时间研究

赵嶷飞，唐华龙

（中国民航大学空中交通管理研究基地，天津300300）

随着机场规模不断扩大和流量持续增长，准确把握拥挤态势成为运行管理中的难题。美国联邦航空局（FAA）和欧洲空管局（EUROCONTROL）采用畅通滑行时间（unimpeded taxi time）作为量化分析机场运行效能的标杆。国内笼统地规定了少数机场的平均滑行时间作为机场运行指标，但无法反映不同机场、不同停机位、不同起飞跑道造成的运行差异。因此可借鉴机场畅通滑行时间这个指标来考核机场效能，但是欧美机场的该指标数值并不完全适合国内机场，因此在欧美计算方法的基础上提出了改进的畅通滑行时间计算方法，并构建多元线性回归模型，运用北京首都机场实际运行数据进行检验，证明了该方法的可行性。

交通拥挤；滑行效率；畅通滑行时间；回归分析

准确识别机场交通拥挤是有效实施运行管理的前提和基础。目前中国采用机场航班时刻容量[1]作为衡量机场拥挤的标杆，欧洲采用机场公布容量（declared capacity）[2]，但2个指标没有考虑运行中各类实际情况，是个静态指标。如北京首都机场航班时刻容量是88架次/h[1]，而实际运行中超过100架次/h时段并不少见，如果采用原有指标数值，则无法反映实际运行中的变化情况。Paul T R提出离场排队延误时间作为衡量机场当前拥挤情况的重要参数[3]，但是离场排队延误主要考虑航路流量控制，因此该指标也有一定局限性。为更准确地计算离场排队延误时间，Cooper引入机场滑行时间标杆——畅通滑行时间（unimpeded taxi time），并将实际滑行时间与畅通滑行时间之差（additional taxi time）作为衡量机场拥挤的关键指标[4]。

FAA对滑行时间的定义为：飞机从推出停机位到起飞离地过程的时间[5]；对畅通滑行时间的定义为：在不受机场地面拥挤、天气等可能影响飞机滑行时间因素的干扰下，一架飞机的滑行时间。以此为基础，FAA和EUROCONTROL都采用实际滑行时间和畅通滑行时间之差来评价机场拥挤和滑行效率[6-8]。

国内目前还没有畅通滑行时间这个指标，只是规定了各个大型机场的平均滑行时间，如首都机场、上海虹桥机场等的滑行时间为30 min[9]。显而易见，这种笼统的规定无法充分考虑不同跑道、不同停机位带来的差异。因此想要对机场地面运行效率进行更深入分析，建立畅通滑行时间标杆是必须的前提和基础，FAA与EUROCONTROL的实践也证明这一指标的适用性。由于篇幅的限制，本文研究的畅通滑行时间仅限于起飞航班的滑出时间（taxi-out time）。

1　研究现状

对畅通滑行时间的计算有3种方法[10-11]：

1）根据每一架飞机的滑行路线、机场跑道布局、停机位分配等详细历史运行数据，采用TAAM、SIMMOD等仿真软件对机场地面的运行情况进行仿真，得出畅通滑行时间。

2）通过设立拥挤指数[2，7，11]，将拥挤指数小于某个拥挤阈值下的飞机作为不受拥挤影响的飞机，计算这些不受拥挤影响飞机的平均滑行时间即为畅通滑行时间。EUROCONTROL性能分析部用此方法对畅通滑行时间进行计算。设立拥挤指数与拥挤阈值的具体方法为首先按照飞机类型（重、中、轻）、跑道和停机位将离场飞机进行分类。统计飞机推出到起飞过程中所有起飞和落地的飞机架次，这个架次数被定义为拥挤指数。将离场飞机滑行时间按照大小排列，取第20百分位数为UT，按照以下公式计算得到拥挤阈值

拥挤阈值=50%（机场最大吞吐量×UT/60）

3）采用计量经济学的方法来估计畅通滑行时间[6-7]，考虑起飞排队飞机数和落地滑入飞机数2个变量，建立线性回归模型。当某架飞机推出时没有地面起飞排队飞机和落地滑入飞机，则表示此飞机的滑行时间不受影响。此时所建立回归模型的常数项即为畅通滑行时间。FAA则用此方法对畅通滑行时间进行计算。

通过对以上3种方法分析可知，仿真方法不仅需要大量实际数据，而且仅能按照指定规则仿真少数几种情况。方法2）和3）完全基于实际运行数据分析，更具参考意义。本文基于方法3）对北京首都机场从机位531到536推出并在跑道36R起飞航班畅通滑行时间进行研究，分别分析起飞排队飞机数和落地滑入飞机数同滑行时间的关系，据此建立关于起飞排队飞机数和落地滑入飞机数的滑行时间多元回归模型，实现对畅通滑行时间的计算。

2　机场运行环境选取

北京首都机场拥有3座航站楼和3条跑道，如图1所示，由西向东分别为跑道36L/18R、36R/18L和01/ 19。跑道36L/16R和36R/18L之间为T1和T2航站楼，跑道36L/16R和01/19之间为T3航站楼。

图1　北京首都机场平面布局Fig.1　Layout of Beijing Capital International Airport

表1为北京首都机场2014年2月至5月的起降架次统计表，01、36L和36R为首都机场主用运行跑道。此外，由于T3航站楼停靠的飞机主要使用36R和01跑道，因此选择36R跑道起降，停靠在531机位到536机位之间的航班作为研究对象（见图1框中区域）。

表1　2月至5月首都机场各跑道的起降次数Tab.1　Volume of departures and arrivals from Feb to May in Beijing Capital International Airport

3　建立畅通滑行时间回归模型

FAA的ASPM（aviation system performance matrix）数据库[7]在统计畅通滑行时间时采用线性回归模型建立地面起飞排队飞机数、落地滑入飞机数同滑行时间的关系，当飞机推出时起飞排队飞机数为0，落地滑入飞机数为0，则得到畅通滑行时间（unimpeded taxi time）。要准确计算畅通滑行时间，首先是建立能够准确估计滑行时间的回归模型，即找到和滑行时间关联性强的解释变量。

3.1起飞排队飞机数对滑行时间影响

Idris在对波士顿机场的研究中指出地面起飞排队飞机数是影响飞机滑行时间的最主要原因[12]。这一结论在首都机场是否适用，将在下文进行验证。另外在计算起飞排队飞机数的方法上Idris与FAA并不一致。因此本文首先按照FAA ASPM和Idris对起飞飞机数（D）的定义，统计并分析首都机场起飞飞机数与滑行时间的关系，构建回归模型，检验以上结论在首都机场适用性。对起飞排队飞机数（D）的定义分别为

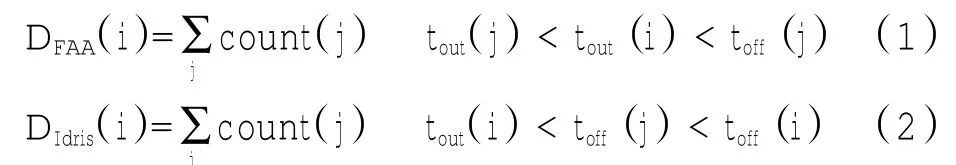
式（1）对起飞排队飞机数的定义为针对某架飞机i，推出时间比i推出时间早并且起飞时间比i推出时间晚的飞机数量。即当i推出时，所有在地面排队等待起飞的飞机数量。式（2）对起飞飞机数定义为针对某架飞机i，在i推出到起飞过程中起飞的飞机数量。

根据式（1）和式（2）两种计算起飞排队飞机数的方法，统计首都机场2月到5月间从停机位531～536推出至跑道36R起飞的飞机起飞排队数，结果分别如图2和图3所示。可以看到滑行时间随着起飞排队飞机数的增加而增长，由图中观察值的分布可以看出，Idris方法的起飞排队飞机数与滑行时间似乎有更强的关联度。下面将通过建立回归模型进一步分析。根据式（1）和式（2）两种方法建立回归模型分别为

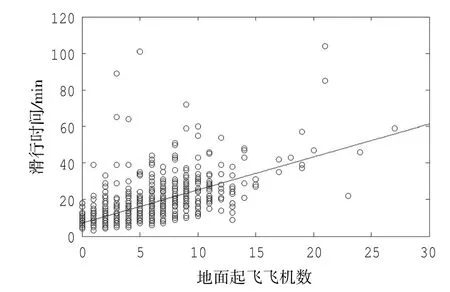
图2　FAA方法地面起飞飞机数和滑行时间关系Fig.2　Correlation between volume of departures and taxi-out time based on US FAA approach

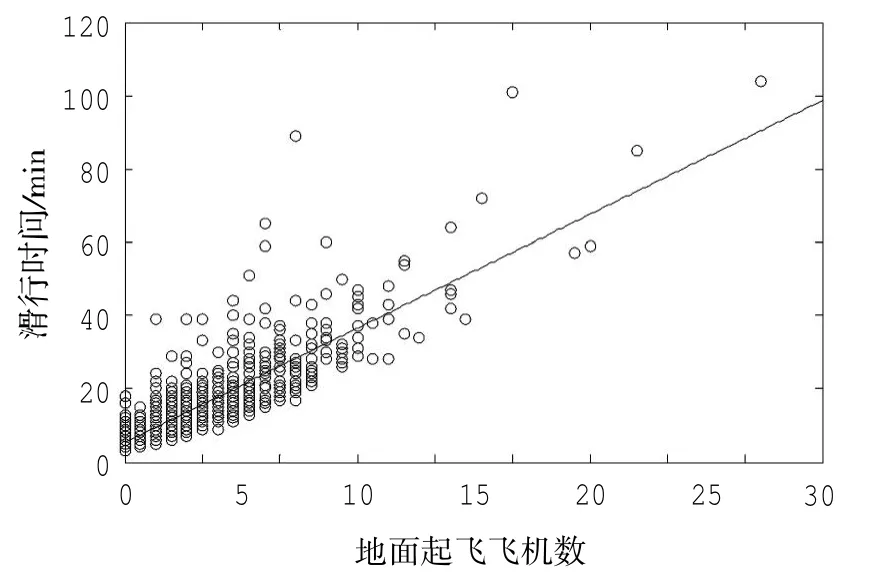
图3　Idris方法地面起飞飞机数和滑行时间关系Fig.3　Correlation between volume of departures and taxi-out time based on Idris approach

根据式（3），得到回归模型R2为0.673 7，由于此处研究某一时间段内起飞飞机数同滑行时间的关系为截面数据，不会有时序数据那么大的R2[13]，因此R2为0.673 7表明采用Idris方法计算的起飞飞机数和滑行时间有更强关联性。表2总结北京首都机场、美国肯尼迪机场和波士顿机场[10]，分别根据式（3）和式（4）建立回归模型的R2。可以看出3个机场在式（3）下回归模型的R2差异较大，但都小于式（4）下回归模型的R2。

表2　基于起飞飞机数的不同回归模型的R2值Tab.2　R2values for regression models based on departing aircraft volume

3.2落地滑入飞机数对滑行时间影响

Idris指出落地滑入飞机数在定量分析中并没有表现出和滑行时间较强的关联性[12]。Idris定义落地飞机数为当某架飞机开始推出的一个时间窗里，已经落地和进入停机位的飞机数，FAA的定义也与其相似[6]。Idris研究发现落地滑入飞机数并不能很好地解释滑行时间（R2仅为0.02），这个结论和所预计的情况相悖。因为滑行时间受制于起飞容量，而根据机场容量曲线可知机场起飞容量受制于降落容量。因此可推断降落容量的改变会导致滑行时间相应变化。Clewlow等人的研究也证实落地滑入飞机数和滑行时间有很强的关联性[10，14]，目前对落地滑入飞机数的研究采用不同的定义，如式（5）～式（8）。

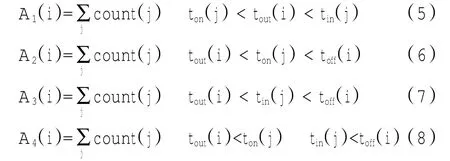
同起飞飞机数的定义类似，式（5）中A1（i）定义为针对飞机i，落地时间比i推出时间早并且到达停机位时间比i推出时间晚的飞机数量，即当飞机i推出时所有落地并滑行的飞机数量。式（6）中A2（i）定义为在飞机i推出至起飞过程中所有落地飞机数量，而式（7）中A3（i）的则为飞机i推出至起飞过程中所有到达停机位的飞机数量。式（8）中的A4（i）为以上两者的交集。

通过线性回归分析可得，A4（i）定义的落地滑入飞机数和滑行时间有最强关联性，其次为A2（i）和A3（i），他们同滑行时间的关联性大小几乎不分上下，而A1（i）定义下的落地滑入飞机数同滑行时间关联性非常低。这表明：A2（i）、A3（i）和A4（i）定义下的落地滑入飞机数实际上与滑行时间有较强关联度，并不同于Idris所说的极低关联性。从图4中落地滑入飞机数同滑行时间的关系也能看出他们之间的关联性。实际上Idris对落地飞机数的定义同A1（i）的定义类似，A1（i）定义下的R2为0.014，同Idris定义下的R2（0.02）十分接近。

图4　A4（i）定义的落地飞机数同滑行时间关系Fig.4　Correlation between volume of arrivals and taxi-out time based on definition A4（i）

上述对北京首都机场的检验结果同Clewlow[10]对美国肯尼迪机场和波士顿机场的研究结果相似。在Clewlow的研究中发现，A2（i）、A3（i）和A4（i）定义下的落地滑入飞机数影响滑行时间，其中定义A4（i）同滑行时间关联度最高，与北京首都机场结果一致。不同回归模型的R2如表3所示。

表3　基于落地飞机数的不同回归模型的R2值Tab.3　R2values for regression model based on arriving aircraft volume

3.3改进回归模型

通过线性回归模型对首都机场起飞排队飞机数、落地滑入飞机数同滑行时间的关联性分析可知：起飞排队飞机数和落地滑入飞机数都是影响滑行时间的重要因素，因此本文将同时考虑2个因素的影响构建多元回归模型。

FAA在建立多元回归模型时对起飞排队飞机数采用式（1）的定义，对落地滑行飞机数采用式（5）定义。通过上文对北京首都机场的分析，FAA采用的解释变量定义并没有体现出其变量和滑行时间很强的关联性。同时发现其他不同定义下的解释变量有更好的关联性表现。

对起飞排队飞机数和落地滑入飞机数采用与FAA不同的定义，起飞排队飞机数（D）采用DIdris定义，落地滑入飞机数（A）分别采用A2（i）、A3（i）和A4（i）定义，运用首都机场截面数据，建立改进回归模型即

多元线性回归模型的系数可看出，每多增加一个降落飞机比多增加一个起飞飞机对滑行时间的影响更大。如式（11）中每增加一个降落飞机，滑行时间相应增加2.57 min；而每增加一个起飞飞机，滑行时间相应增加1.58 min。另外多元线性回归模型的R2得到明显提升（3个模型的R2都达到了0.8，高于之前任何基于起飞排队飞机数和落地滑入飞机数模型的R2）。此结果表明多元线性回归模型能很好地对数据进行拟合，估计滑行时间。不同回归模型的R2如表4所示。

表4　改进回归模型的R2值Tab.4　R2values for improved regression model

为能更好地看到模型改进后R2的变化，具体的计算结果如表5所示。表中第1列分别为3种改进模型（T1、T2、T3）和FAA模型（TFAA）；第2列为基于起飞排队飞机数的各模型R2值；第3列为基于落地滑入飞机数的各模型R2值；第4列为基于以上两个变量的模型R2值。FAA模型的R2仅为0.371 8，而改进模型的R2有了很大提升，能够更好地估计畅通滑行时间。

表5　改进回归模型和FAA模型R2值对比Tab.5　Comparison of R2values between improved regression model and FAA model

4　估计畅通滑行时间

通过以上回归分析可知，基于式（11）的回归模型R2最高，因此本文采用基于式（11）的线性回归模型估计畅通滑行时间。针对某架飞机i，当起飞排队飞机数和落地滑入飞机数都为0时，即没有起飞排队的飞机和落地滑行的飞机对飞机i的滑行造成影响，式（11）在Y轴上的截距则为畅通滑行时间。因此可以得到首都机场从停机位531到536之间推出，并在跑道36R起飞的飞机畅通滑行时间为4.82 min。滑行时间的分布情况如图5所示，几乎所有飞机的滑行时间都大于畅通滑行时间，仅有4架飞机的滑行时间小于畅通滑行时间（虚线下方区域）。

图5　滑行时间分布Fig.5　Distribution of taxi-out time

5　结语

对不同定义下的起飞排队飞机数和落地滑入飞机数同滑行时间的关联性进行验证，发现不同定义下起飞排队飞机数与落地滑入飞机数对滑行时间影响作用不同。其中起飞排队飞机数定义为针对某架飞机i推出到起飞过程中其他起飞飞机数，落地滑入飞机数定义为针对某架飞机i推出到起飞过程中其他落地并进入机位飞机数，与滑行时间关联性最大。并据此建立包含这2个解释变量的多元线性回归模型，此模型较其他回归模型，特别是比FAA采用的模型拟合度更好。因此利用此模型对北京首都机场从机位531到536推出并在跑道36R起飞飞机的畅通滑行时间进行估计，结果为4.82 min。分析2月至5月滑行时间分布，仅4架飞机的滑行时间小于畅通滑行时间。

本文仅研究了从首都机场某一停机位区域到某一跑道的畅通滑行时间，未来将进一步研究对不同停机位—跑道组合、不同跑道运行模式或在其他影响滑行时间因素干扰下的畅通滑行时间。另外对滑行效率的评价不仅仅是一个指标，还需进一步研究评价指标体系。

[1]中国民用航空局.关于公布协调机场航班时刻容量的通知（局航明发[2012]1990号）[G].北京：中国民用航空局，2012.

[2]EUROCONTROL.ATM Airport Performance（ATMAP）Framework-Measuring Airport Airside and Nearby Airspace Performance[R].Brussels,2009.

[3]PAUL J A,BATTA R,LIN L,et al.Airport Security System Design：Passenger Flow Analysisand SimulationModeling[M]//PAUL S,FRANCIS X S.Protecting Airline Passengers in the Age of Terrorism,Goleta: ABC-CLTIO,2009:184-206.

[4]COOPER W W，CHERNIAVSKY E A，DEARMON J S，et al.Determinationof MinimumPush-backTimePredictabilityNeededforNear-term Departure Scheduling Using DEPARTS[C]//Proceedings of the Fourth USA/Europe Air Traffic Management Seminar ATM-2001,Santa Fe NM.2001.

[5]FAA.ASPM Taxi Times:Definitions of Variables[EB/OL].（2015-07-05）.[2015-09-15].http://aspmhelp.faa.gov/index.php/ASPM_Taxi_Times: _Definitions_of_Variables.

[6]ZHANG Y,WANG Q.Applying Regression Models to Benchmark Airport Taxiing Performance Indicators[C]//11th International Conference of Chinese Transportation Professionals（ICCTP）,2011.

[7]EUROCONTROL,FAA.US/Europe Comparison of ATM-Related Oprational Performance 2010[R].Brussels/Washington D C,2010.

[8]EUROCONTROL,FAA.US/EuropeComparison of ATM-Related Oprational Performance 2013[R].Brussels/Washington D C,2013.

[9]中国民用航空局.关于印发民航航班正常统计办法的通知（民航发（2012）88号）[Z].北京：中国民用航空局，2012.

[10]CLEWLOW R,SIMAIAKIS I,BALAKRISHNAN H.Impact of Arrivals on Departure Taxi Operations at Airports[C]//Proceedings of the AIAA Guidance,Navigation,and Control Conference,2010.

[11]GARCIA-CHICO J.Reviewing Airport Performance：Evaluating a Methodology to Measure Time Efficiency in the Taxi-Out Phase[C]//11th AIAA AviationTechnology,Integration,and Operations（ATIO）Conference,2011.

[12]IDRIS H R,DELCAIRE B,ANAGNOSTAKIS I,et al.Identification of Flow Constraint and Control Points in Departure Operations at Airport Systems[C]//AIAA Guidance，Navigation and Control Conference.1998.

[13]赵松山.对拟合优度R2的影响因素分析与评价[J].东北财经大学学报，2003（3）：56-58.

[14]CHENG S,ALCABIN M,FRACCONE G C,et al.Developing a Baseline for Taxi Operations at US Domestic Airports[C]//12th AIAA Aviation Technology,Integration,and Operations（ATIO）Conference and 14th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, 2012.

（责任编辑：刘智勇）

Aircraft unimpeded taxi time in Beijing Capital International Airport

ZHAO Yifei,TANG Hualong
（Air Traffic Management Research Base,CAUC,Tianjin 300300,China）

Given consistent expanding airport size and increasing air traffic flow,accurately apprehending the traffic congestion situation in operation management becomes a vital problem.In China only a few airports′average taxi out time is specified as the indicator of airport operation.However,it cannot recognize the difference between various combinations of gates and departure runways in one specific airport.The unimpeded taxi time is introduced as an optimum reference in FAA and EUROCONTROL in order to evaluate the level of inefficiencies in the taxi-out phase.Nevertheless,the value of unimpeded taxi time in US or Europe is not suitable for airports in China.Based on FAA and EUROCONTROL approaches,an improved one on which multiple linear regression models is built, is proposed to evaluate the unimpeded taxi time.Validaton of this approach with operational data in Beijing Capital International Airport proves its feasibility.

traffic congestion;taxi-out efficiency;unimpeded taxi time;regression analysis

V355.2

A

1674-5590（2016）04-0001-05

2015-07-05；

2015-10-08基金项目：国家自然科学基金项目（U1433111）

赵嶷飞（1971—），男，湖南常德人，教授，博士，研究方向为空中交通规划与管理.