浅析定积分的计算和应用

2016-10-22牛艳秋

赤峰学院学报·自然科学版 2016年18期

关键词：正电荷莱布尼茨原函数

牛艳秋

（吉林建筑大学城建学院，吉林　长春　130111）

浅析定积分的计算和应用

牛艳秋

（吉林建筑大学城建学院，吉林长春130111）

定积分是高等数学的一个重要的基本概念，本文主要讨论定积分的计算和应用，对一些应用的方法和技巧进行分析和总结，进一步讨论了定积分在几何、物理、经济学等各领域的广泛应用.

微分；积分；计算；应用

微积分的两大部分是微分和积分，两个基本定理和牛顿—莱布尼茨公式说明了微分和积分的联系：

第一基本定理：设函数f（x）在［a,b］上连续，x∈［a,b］，则变上限积分,对x求导，并且有

第二基本定理：设函数f（x）在［a,b］上连续，x∈［a,b］，则是f（x）的一个原函数.

它告诉我们，一个连续函数f（x）的原函数不止一个，有无穷多，其中任意两个原函数只相差一个常数，因为ø（x）=是f（x）的一个原函数；所以如果F（x）是f（x）的另一个原函数，那么必有在此基础上，推得了牛顿—莱布尼茨公式

众所周知，想用定积分定义来求定积分的值是十分困难的，甚至不可能，而应用牛顿—莱布尼茨公式来计算定积分就会非常简便，它把定积分的计算方法转化为求被积函数f（x）的任意一个原函数，或者说求f（x）的不定积分，因为不定积分是f（x）的任意一个原函数的代表，所以不定积分在微积分学中也占有重要地位和作用.

1　定积分的计算方法

定积分的计算通常会采用以下三种计算方法来计算：

注意：在换元过程中，必须更换积分上、下限.（换元必换限）

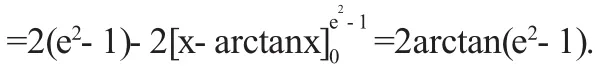
2　定积分的应用

定积分的概念实质上是从实际问题中抽象而来的，因此它在几何、物理、及经济学上有广泛的应用.

定积分的所有应用问题都具有一个固定的模式：求与某个区间［a,b］上的变量f（x）有关的总量Q.这个量Q可以是面积，体积，弧长，功等.我们用如下的步骤去确定这个量.

1°分割.用分点

a=x0＜x1＜…＜xn=b将［a,b］分为n个子区间.

2°近似.找一个连续函数f（x），使得在第i个子区间［xi-1, xi］上，Q可以用量f（ξi）（xi-xi-1），ξi∈［xi-1,xi］，（i=1,2,…n）来近似，这一步是问题的核心.

3°求和.将所有这些近似量加起来，得总量Q的近似值

4°取极限.当分割无限细密时，得出

对上面的求积过程可作如下的较为简捷的处理.f（ξi）用f（x）代替，Δxi用dx代替，和号Σ用积分号∫代替，即用

我们已经指出，第二步的“近似”是关键.我们在具有代表性的任一小区间［x,x+dx］上，以“匀代不匀”找出微分

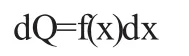
然后从a到b积分，就可求出量Q.这种在微小的局部上进行数量分析的方法叫做微元法.

2.1定积分在几何上的应用

在此类题中我们采用的就是微元法，前面我们对微元法进行了分析，下面我们以解题的方式，来进一步诠释微元法的妙用：

例题求y=sinx；y=cosx；x=0以及x=2π所围平面图形的面积（见图）.

2.2定积分在物理学中的应用

例题把一个带电荷量+q的点电荷放在r轴上坐标原点O处，它产生一个电场，这个电场对周围的电荷有作用力.由物理学知道，如果有一个单位正电荷放在这个电场中距离原点O为r的地方，那么电场对它的作用力的大小为（k为常数）见图，当这个单位正电荷在电场中从r=-a处沿r轴移动到r=b（a＜b）处时，计算电场力F对它所作的功.

解在上述移动过程中，电场对这单位正电荷的作用力是变的，取r为积分变量，它的变化区间为［a,b］，设［r,r+dr］为［a,b］上的任一小区间，当单位正电荷从r移动到r+dr时，电场力对它所作的功近似于，即功元素为于是所求的功为

2.3定积分在经济学中的应用

例题已知生产某产品x单位时的边际收入为R'（x）=100-2x（元/单位）,求生产40单位时的总收入及平均收入,并求再增加生产10个单位时所增加的总收入.