基于贪心遗传混合算法的仓库货物集成分配研究

张昊，王飞

（河海大学商学院，江苏南京211100）

基于贪心遗传混合算法的仓库货物集成分配研究

张昊，王飞

（河海大学商学院，江苏南京211100）

针对运输车辆和仓库装卸吊车作业的合理分派与调度问题，考虑抵达仓库的运输车辆的停靠总时间和平均装卸吊车迁移次数为目标，在偏好车位的约束条件下，建立连续车位和装卸吊车分配的规划模型。利用贪心算法和遗传算法相结合的方式，设计了一种混合进化算法提高仓库货物平台的作业效率。最后的仿真求解结果表明：相对于贪心算法，平均收敛代数优化率达到86.7%；相对于遗传算法，平均收敛时间优化率达到17.9%；该算法能够在可接受的计算时间内获得稳定的满意解，新的车位和装卸吊车分配策略较好的解决了偏好车位约束条件下的货物集成分配问题。

贪心算法；遗传算法；货物集成；货物分配

仓库被看成一个无附加价值的成本中心，而现在仓库不仅被看成是形成附加价值过程中的一部分，而且被看成是企业成功经营中的一个关键因素［1］。仓库管理各个环节管理确保企业及时准确地掌握货物的调度信息，合理管理货物库存［2］。而仓库货物的集成与分配合理化调度是企业的重要组成部分［3］，仓库货物平台作为企业日常货物运输的关键节点，必将会发挥更大的作用［4］。仓库的车位分配问题是提高货物平台运营效率的一个重要因素［5］，与之衔接的装卸吊车分配问题则是货物装卸作业的关键［6］。车位和装卸吊车是企业的仓库货物平台资源，如何处理好有限的车位、装卸吊车资源和运输车辆的需要三者时间的矛盾，是仓库作业计划中的一个重要问题。在实际作业中装卸吊车数量和装卸吊车的成本限制，仓库需要在最大限度的装卸吊车数量和有限车位下，进行集成货物优化配置来提高运行效率。

本研究从运输车辆的等待时间，成本最低的停靠位置，离开时间，装卸吊车的移动时间和装卸作业效率等几方面来研究仓库货物分配问题，利用抵达仓库的运输车辆的停靠总时间和平均装卸吊车迁移次数构建目标函数，在偏好车位的约束条件下，建立连续车位和装卸吊车分配的规划模型。利用贪心算法和遗传算法相结合的方式，设计了一种混合进化算法提高仓库货物平台的作业效率。

1　仓库货物集成与分配建模

1.1问题描述

运输车辆抵达仓库，仓库月台调度员将根据相关信息和调度策略将车位和货物平台分配给车辆。考虑到车位与货物平台分配问题为动态性和连续性［7-8］，只要运输车辆条件满足停靠的月台长度，车辆便可沿连续货物平台停靠，多辆运输车辆可以同时停靠月台。本研究提出的目标函数综合3个方面的因素：对运输公司而言，希望到达的车辆被分配到理想的偏好车位且处理时间延误最小；对月台管理人员而言，希望到达仓库的运输车辆数量和货物吞吐量能最大。当车辆停靠时，占用车位单元数取决于其车长，占用时间取决于货物平台装卸处理时间。本研究将月台视为连续的车位，考虑的抵达车辆等待装卸时间的约束条件，以最小化车辆总在车位时间和最小化平均月台移动次数为目标，建立的连续车位和装卸吊车集成分配模型将基于如下合理假设：

1）每辆运输车辆必须被服务且被服务一次（不考虑车位的移动），且处理时间取决于所在车位、货物平台的装卸吊车数量，与车辆的距离、货物运输以及其他因素等无关；

2）车位资源视为连续线性的，被划分为尽可能多且相等的微小停靠单元，多辆运输车辆可以同时停靠；

3）每辆车设有同时作业的最大装卸吊车数和最小装卸吊车数，当可用装卸吊车数量不小于最小装卸吊车数时才能开始作业，并且不能大于最大装卸吊车数，且分散的闲置装卸吊车不能横跨工作，装卸吊车只能在货物平台固定的位置为停靠的车辆进行装卸；

4）每辆运输车都有一个最优停靠偏好位置，偏离偏好车位会增加停靠时长，车位计划在零时刻开始，车辆只有抵达车位才能进行装卸作业。此外，车辆停靠作业过程中的停靠时间和离开时间对于不同运载量的车辆差异不大，且相对整个停靠时间很小，在此忽略不计。

1.2模型建立

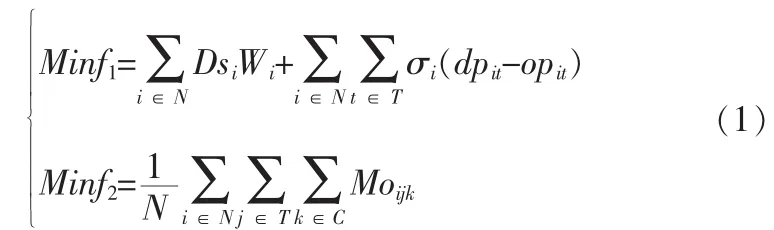
其中，L为连续货物平台的总长度，Hci为车辆i要处理的货物量，nit在t时刻服务车辆i的装卸吊车数量，di为车辆i的离开时间期望，Bi为车辆i的实际开始处理时间。车辆抵达仓库后才能开始被服务，且车辆的装卸时间与装卸吊车的数量和作业速度有关。最后对货物平台连续车位偏好位置的定义。则约束条件为：

如果车辆i完全位于车辆j的左侧，则εij=1，否则为0。如果车辆i完全位于车辆j的后方，则ζij=1，否则为0。则车辆i和j在时空图中的位置不重叠，即车辆i和j在货物平台连续月台上不能停靠在同一位置上。约束条件如下：

若能够同时分配给车辆的最小装卸吊车数和最大装卸吊车数分别为和，则每辆运输车分配的装卸吊车数的范围为：

在时间段j内，如果装卸吊车k为车辆i服务，则取λijk=1，否则为0。其中C=｛1，2，…，c｝为可利用装卸吊车数的集合。则确保每个时间段一台装卸吊车最多只为一辆车服务，且每个时间分配给车辆的装卸吊车数不能超过总的装卸吊车数，则约束条件为：

车辆i等待停靠的时间和等待装卸吊车的时间分别为Wi和Wci，车辆i等待排队进仓库的参数为Mli，则限制每辆运输车辆的等待时间小于其最大可接受的等待时间约束条件为：

2　贪心遗传混合算法

容忍度约束下连续运输车辆和装卸吊车作业集成分配问题主要由两个子问题组成，即车位分配问题与装卸吊车分配问题。本研究设计了一种基于贪心算法和遗传算法的混合进化算法［9］，贪心算法生成相应的车位调度计划，遗传算法生成相应的装卸吊车调度计划。

2.1贪心算法

贪心策略就是指它在每一步都做出当时看起来最佳的选择［10］，它总是做出局部最优的选择，寄希望这样的选择能导致全局最优解［11-12］。对于陆续抵达仓库的车辆建立两个集合，分别命名为Set A，Set B。Set A代表陆续抵达的车辆集合，Set B代表抵达仓库后已分配车位的车辆集合。每辆抵达仓库的运输车辆都有一个实际抵达时间ai和一个离开时间期望di。把陆续抵达仓库的车辆加入到Set A集合中，然后根据贪心策略选择Set A中的车辆把它加入到Set B中去，贪心算法步骤：

Step1：初始化各集合：Set A，存放抵达仓库待处理的车辆集合，其初始化大小就是抵达车辆的总条数；Set B，初始化为空；

Step2：判断Set A集合是否为空，若为空，程序结束；

Step3：获取当前车位的占用现状，以及Set A中车辆的偏好车位等参数；

Step4：利用贪心策略从Set A中选择一辆运输车辆，使得该车辆停靠后的目标函数值最小；

Step 5：将停靠的车辆从Set A中删除，加入到Set B中，转向Step2。

2.2遗传算法

通过遗传算法产生决策变量［13］，然后运用装卸吊车启发式算法在每一代中产生从属变量。染色体编码中每个基因的位置表示车辆的ID，相应的值表示在满足公式（4）的约束条件下随机产生的决策变量n。装卸吊车分配问题仍是一个最小化问题，因此它的目标函数值转换为适应度函数：

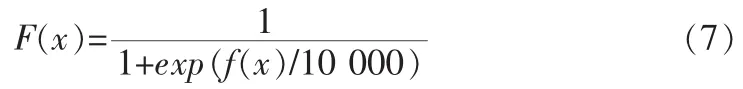
由于车辆停靠货物平台的随机性较大，有时会使基因出现“退化”现象，即采用轮盘赌的选择策略［14］，使得适应度较高的基因失去选择的机会，使得收敛到最优解。交叉操作采用两点交叉法［15］，其交叉后得到的子代满足公式（5）的约束条件。在获得车辆i的车位位置（xi，xi+li）和当前车位调度计划中的时间窗（yi，ci）后，根据遗传算法获取分配给运输车辆i的装卸吊车数n。假设位置基因选出的要参加交叉的粒子为xi，则有目的的选取的交叉粒子为：

其中，α＞0为步长因子，‖xi-xi′‖表示两个基因粒子之间的二范数。采用取代变异的方法［16］，即随机的选择一个取代位置，并用当前个体中满足公式（5）约束条件的基因信息取代当前位置上的基因信息。当达到设定值的最大迭代次数，算法终止并输出结果然后，检查相应车位空间（xi，xi+li）上空闲的装卸吊车数量C，如果C≥n，选择合适的装卸吊车从前往后依次分配给船舶i；如果C＜n，则在满足没有交叉的前提下，从邻近位置移动装卸吊车到所须位置，直到满足所需的装卸吊车数量。

3　算例验证

3.1参数设置

仓库货物平台选取了月台长为120米的连续车位，装卸吊车总数为5，有12辆运输车辆陆续抵达仓库，并以第一辆抵达仓库车辆的抵达时间为基准0，具体算例如表1所示。

表1　参数假设

3.2模拟对比

在分析时若考虑车辆偏好车位、等待时间和装卸吊车移动策略对停靠计划的影响，车辆的等待时间、目标函数值都是最小的；反之，车辆的等待时间、目标函数值最大。由此反映了车辆的偏好车位、等待时间以及装卸吊车迁移策略对停靠过程中车辆的等待时间与在仓库货物平台总时间成本有较大的影响，验证模型与算法的有效性。本研究将从以下3个方面验证算法的有效性，对比分析如表2所示。

表2　对比分析

根据表2模拟的3种情景分别对比分析：

情景1：综合考虑车辆偏好车位、等待时间以及装卸吊车迁移策略对停靠计划的影响。根据算例数据，经求解可得偏所有车辆总的等待时间t=22，所有车辆总在停靠的时间成本f=93.29。

情景2：不考虑车辆偏好车位、等待时间对停靠计划的影响，只考虑装卸吊车迁移策略对车辆停靠计划影响。根据算例数据，经求解可得所有车辆总的等待时间t=67.13，所有车辆总在港的时间成本f=105.22。

情景3：不考虑船舶偏好车位、等待时间对停靠计划的影响，也不考虑装卸吊车迁移策略对车辆停靠计划影响。根据算例数据，经求解可得所有车辆总的等待时间t=67.13，所有车辆总在港的时间成本f=127.50。

3.3性能对比

为了分析本研究贪心遗传混合算法中选择策略的选取合理性，实验过程中分别贪心算法和遗传算法分别与本研究的算法进行比较。并且将基于以上选择策略的。参数的取值均为表1所示，在相同参数取值下每组实验重复10次，取相应的平均收敛代数和平均收敛时间。如表3所示。

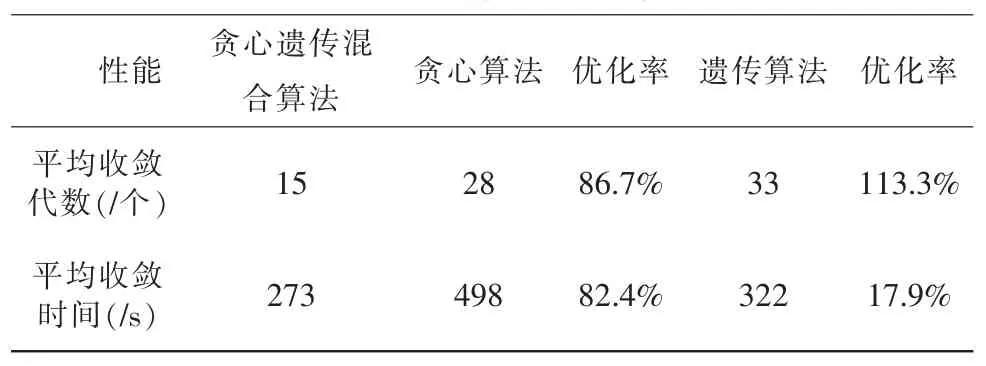
表33　种算法性能比较

从表3可知，基于贪心遗传混合算法具有最小的平均收敛代数为15，且平均收敛时间为273s，平均收敛代数表现上，贪心算法仅次于贪心遗传混合算法，优化率为86.7%；而平均收敛时间表现上，遗传算法需要仅次于贪心遗传混合算法，优化率为17.9%。分析其原因，主要是因为在贪心算法中较小的位置基因规模中未能发挥出优势；而遗传算法在演化代数内并不能考虑到所有的货物集成分配因素。正基于以上原因，在仓库的货物集成分配中选择贪心遗传混合算法。

4　结论

本研究在仓库货物集成分配研究的基础上，引入运输车辆抵达仓库等待装卸时间的策略，考虑抵达仓库的运输车辆的停靠总时间和平均装卸吊车迁移次数构造目标函数。分别利用贪心算法生成相应的车位调度计划，遗传算法生成相应的装卸吊车调度计划，该贪心遗传混合算法综合模拟仓库货物集成与分配。最后在平均收敛代数和平均收敛时间方面，比较了贪心算法、遗传算法与贪心遗传混合算法的性能。结果显示，贪心遗传混合算法在平均收敛代数和平均收敛时间上均优于其他两种算法，说明该混合算法可作为企业的仓库货物集成与分配的参考性分析。

［1］张彦嘉.X制造企业仓库规划与管理研究［D］.大连：大连海事大学，2014.

［2］唐佳莹，张瑞林，季君君，等.RFID在纺织企业仓库管理系统中的应用［J］.物联网技术，2012（9）:28-30.

［3］杨文强，邓丽，费敏锐，等.基于改进禁忌搜索的多目标自动化仓库调度［J］.计算机集成制造系统，2013（8）:2097-2104.

［4］杨铭，秦华容，陈荫三.区域公路货物周转量结构分析与推算方法［J］.交通运输工程学报，2011（5）:93-100.

［5］邢丽娟，李建国.立体车库车位分配仿真与分析［J］.铁路计算机应用，2011，20（10）:32-34.

［6］郑忠，周超，陈开.基于免疫遗传算法的车间天车调度仿真模型［J］.系统工程理论与实践，2013，33（1）:223-229.

［7］李晓君，谢新连.重大件运输的货物分配与航速联合优化［J］.西南交通大学学报，2015，50（4）:747-754.

［8］周华.基于电子标签的物流货物自动分配策略设计［J］.自动化与仪器仪表，2016（1）:104-105.

［9］王友钊，彭宇翔，潘芬兰.基于贪心算法和遗传算法的仓储车辆调度算法［J］.传感器与微系统，2012，31（10）:125-128

［10］聂长海，蒋静.覆盖表生成的可配置贪心算法优化［J］.软件学报，2013（7）:1469-1483.

［11］宫国顺.贪心算法在P类问题求解中的应用［J］.电脑知识与技术，2011，7（2）:444-446.

［12］李宝磊，施心陵，苟常兴，等.多元优化算法及其收敛性分析［J］.自动化学报，2015，41（5）:949-959.

［13］马永杰，云文霞.遗传算法研究进展［J］.计算机应用研究，2012，29（4）:1201-1206.

［14］魏波，喻飞，徐星，等.基于改进轮盘赌策略的交互式演化算法［J］.计算机与数字工程，2014（10）:1763-1767.

［15］刘大莲，徐尚文.求解约束优化问题的内外交叉遗传算法［J］.系统工程理论与实践，2012，32（1）:189-195.

［16］闭应洲，陆建波，丁立新，等.基于有导向变异算子的GM-EA算法［J］.计算机应用研究，2010，27（4）:1249-1251.

Study on the integrated distribution warehouse based on blend of genetic and greedy algorithm

ZHANG Hao，WANG Fei
（Business School，Hohai University，Nanjing 211100，China）

For the truck and warehouse loading and unloading crane of reasonable assignment and scheduling problem considering arrived in warehouse transport vehicles docked total time and the average loading crane migration times as the goal，under the constraints of the preference of parking spaces，the establishment of continuous parking and loading and unloading crane allocation programming model.Using the greedy algorithm and genetic algorithm combination，designed a hybrid evolutionary algorithm to improve the efficiency of warehouse cargo platform.Finally the simulation to the results show that:compared with the greedy algorithm，optimizing the average Algebraic Convergence rate reached 86.7%；compared with the genetic algorithm，average convergence time optimization rate reached 17.9%；the algorithm can obtain satisfactory solutions in acceptable computation time，new parking and loading and unloading crane allocation strategy better solves the parking preference constraint goods integrated allocation problem.

greedy algorithm；genetic algorithm；integrated of goods；distribution of goods

TN01

A

1674－6236（2016）17-0007-04

2016-02-28稿件编号：201602179

国家自然科学基金项目（71372166）；江苏高校哲学社会科学研究重点项目（2010ZDIXM004）

张昊（1992—），男，吉林大安人，硕士研究生。研究方向：财务管理。