基于模糊双曲正切模型的短期光伏发电量预测

齐红云，伦淑娴

（1.渤海大学工学院，辽宁锦州121013；2.渤海大学新能源学院，辽宁锦州121013）

基于模糊双曲正切模型的短期光伏发电量预测

齐红云1，伦淑娴2

（1.渤海大学工学院，辽宁锦州121013；2.渤海大学新能源学院，辽宁锦州121013）

通过对影响光伏发电量产生的因素进行分析比较，在模糊双曲正切模型的基础上，建立一种光伏发电量的短期预测模型。该模型既属于模糊模型，也属于神经网络模型的范畴。可以利用其强大的学习能力，以光伏发电系统的历史数据作为训练样本，对模型进行学习，并利用得到的稳定模型对光伏发电量进行短期预测。仿真结果表明，该预测模型与其他预测方法相比有更高的预测精度。

光伏发电量；短期预测；模糊双曲正切模型；预测精度

由于全球能源危机越来越严重，人们加快了对新能源探索和开发的脚步。太阳能作为新能源和可再生能源的重要组成部分，受到越来越多国家的重视［1-3］。太阳能是一种清洁能源，已被公认为是未来最具竞争力的能源之一。光伏发电量预测是太阳能利用的一项重要指标，但是由于光伏阵列的输出会受到温度、光照强度、风速等外界因素的影响，会造成光伏发电量的不确定性，从而使并网运行后对电网的安全、稳定和电网的供电质量造成一定的冲击，因此研究光伏发电量预测具有重要的意义。

从20世纪80年代开始，随着光伏发电量在各国电网中所占比例逐渐增大，越来越多的专家学者致力于研究并改进光伏发电的预测方法，希望可以提高光伏发电站的发电能力。就目前来说，关于光伏发电输出功率预测的方法有很多种，按照研究过程可以分为直接预测和短期预测［4］；而根据时间的长短又可划分为中长期、短期和超短期预测。另外还有数学统计预测法［5-9］，人工智能预测法法［10-16］等。

为了使光伏发电量的预测达到更高精度，在模糊双曲正切模型的基础上，我们提出一种光伏发电量的短期预测方法。

1　模糊双曲正切模型

模糊双曲正切模型（FHM）被Zhang和Quan于2000年提出，其结构简单，可用于依据日趋成熟的线性系统理论来设计强鲁棒性的稳定控制器。在其后几年，Zhang和Quan又陆续提出广义双曲正切模型等FHM的一系列拓展和应用。其中，依据该模型设计的控制器在理论上可以使系统达到最优性能，因为FHM是一种全局模型。同时，FHM也属于神经网络模型的范畴，因此可以根据神经网络强大的学习能力来优化模型的参数。

对复杂系统来说，难以获得较为准确的数学模型，因此根据经验知识来获取被控对象的数学模型就显得尤为重要。用FHM来描述系统时，其状态方程为

其中，x=（x1，x2…xn）T表示状态变量，u=（u1，u2…up）T表示输入变量，A∈Rn×n，B∈Rn×p为定常矩阵，且kxi为正常数。式子（1）被称作模糊双曲正切模型。

FHM在本质上也属于模糊模型，如果给出合适的隶属函数、模糊化和解模糊的方法，和相应的模糊规则基等，就可以推得该模型。因此，首先定义此模型的模糊规则基。

定义1：假设系统的输入变量用u=（u1（t）u2（t）…up（t））T来表示，状态变量用x=（x1（t）x2（t）…xn（t））T来表示，我们称满足以下条件的的模糊规则基为双曲正切型模糊规则基［19-20］。

1）模糊规则基为如下形式：

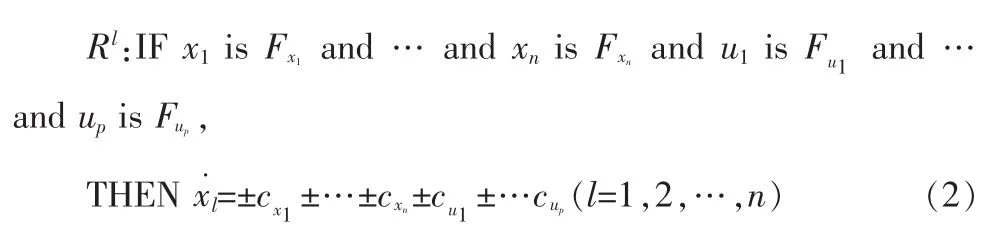
其中，Fxi（i=1，2，…，n），Fuj（j=1，2，…，p）是模糊子集，分别与xi和uj对应，包括正（P）和负（N）两种语言值；cxi和cuj是正常数，分别与Fxi和Fuj对应：当Fxi或Fuj为P时，cxi或cuj前面的符号就是正号；当Fxi或Fuj为N时，cxi或cuj前面的符号就为负号。

2）IF中的状态x，输入u和THEN中的输出项都是可以选择的，但是输出项中的cxi或cuj与x或者u是一一对应的关系，即若在IF部分包含Fxi或Fuj项，那么在THEN部分必然包含cxi或cuj；相反地，若IF部分不包括Fxi或Fuj项，那么在THEN部分也必然不含cxi或cuj项。

定理：给出双曲正切型模糊规则基，若Pz和Nz（z表示状态x或输入u）对应的隶属函数分别定义为如下形式：

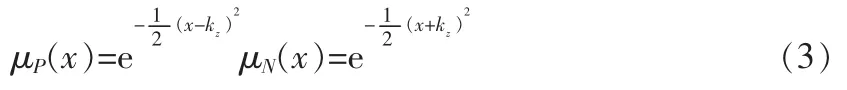
其中kZ是常数，并且kZ＞0。若模糊化采用单点模糊集合，清晰化采用加权平均法，直积运算采用求积法，那么根据模糊规则集定义1可得出如下数学模型：

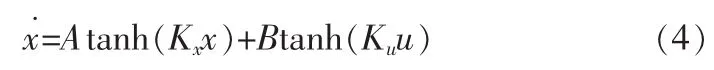
2　基于FHM的光伏发电量短期预测模型

光伏发电系统的输出功率容易受到环境因素的影响，从而使发电量具有不确定性，容易对电网造成冲击。图1至图2分别代表4个不同城市一年内每个月的平均温度和总的辐射强度的变化。表1表示4个不同国家一年中每个月的平均风速。对比图1和图2我们可以知道，当温度高时，相应的辐射强度也高，而由于美国、西班牙和印度均位于北半球，而澳大利亚属于南半球，故而，澳大利亚每个月的平均温度和总辐射量与其他3个国家呈相反趋势。由于每个地方影响光伏发电量的风速、温度、辐射强度等外界因素都不同，而它们都对发电量的产生造成了不同程度的影响，因而，我们在对不同的地方进行光伏发电量预测时，要根据实际情况具体分析。

表1　不同地域的四个国家一年中每个月的平均风速

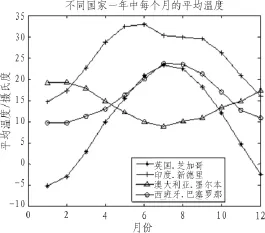
图1　不同地域的4个国家一年中每个月的平均温度

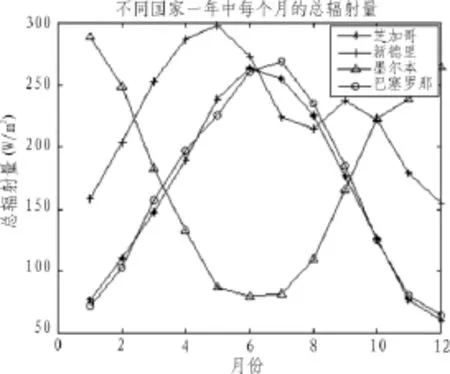
图2　不同地域的4个国家一年中每个月的总辐射强度

由上可知，影响光伏发电量的产生的因素有很多。为了使光伏发电量的预测达到更高精度，我们以辐射强度，温度和风速作为输入，光伏发电量作为输出，建立一种基于模糊双曲正切模型的光伏发电量短期预测模型。

为保证预测精度，我们对历史数据进行筛选，剔除里面的奇异值，从而提高模型的泛化能力。同时，为了使输入输出数据能保持在0～1范围内，我们对数据进行归一化处理，

在对所建立的预测模型进行学习的过程中，我们用平均绝对百分比误差（MAPE）来判断预测模型的好坏，这是目前常用的评估性指标，其表达式如下：

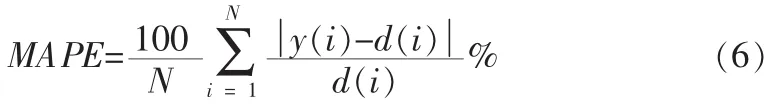
其中，d（i）代表期望值，y（i）代表预测值，N代表训练样本的大小，i代表第i次训练。

3　仿真结果分析

我们选择2005年美国阿拉斯加州的科策布（北纬66.883°，西经162.6°）为观测点得到的数据作为研究对象。在进行试验之前，我们需要初始化程序。我们选择一年中每天8: 00-17:00的地球表面辐射强度、温度和风速作为样本输入，光伏发电量作为样本输出，初始样本长度设为300，采样样本长度设为200。下面我们分别构建BP神经网络预测模型，标准ESN预测模型，FHM预测模型，通过仿真实验，我们可以的几种预测模型的预测效果如下：

通过观察表2，我们可以知道当利用BP神经网络预测模型对光伏发电量的输出功率进行预测时，预测结果MAPE= 0.31%，而标准ESN预测模型和FHM预测模型的预测精度相比BP神经网络模型来说明显提高，尤其是本文所提出FHM预测模型，其预测精度是BP神经网络模型的27.7倍，预测性能大大提高。

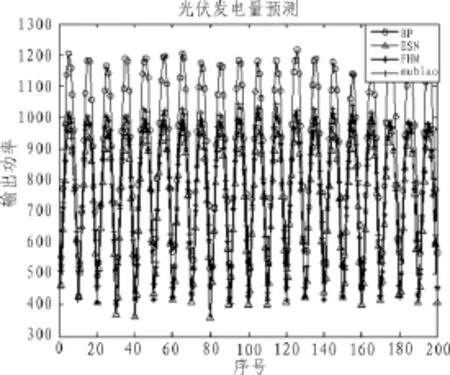
图3　不同模型的预测效果

表2　不同模型的预测性能（MAPE）

4　结论

文中通过分析影响光伏发电量的外界因素，建立不同的预测模型来对光伏发电量进行预测。通过具体的仿真实验来比较不同预测模型的预测性能，证明了本文所提出的FHM模型对于光伏发电量预测有更高的预测精度，验证了所提模型的有效性。

［1］Lun S X，Du C J，Guo T T，et al.A new explicit I-V model of a solar cell based on Taylor's series expansion［J］.Solar Energy，2013（94）：221-232.

［2］Lun S X，Du C J，Yang G H，et al.An explicit approximate I-V characteristic model of a solar cell based on padé approximants［J］.Solar Energy，2013（92）：147-159.

［3］Romero B，Pozo G del，Arredondo B，Exact analytical solution of a two diode circuit model for organic solar cells showing S-shape using Lambert W-functions［J］.Solar Energy，2012（86）：3026-3029.

［4］袁晓玲，施俊华，徐杰彦.计及天气类型指数的光伏发电短期出力预测［J］.中国电机工程学报，2013，33（34）：57-64.

［5］秦俊举，张恕远.一种新的光伏发电预测模型的设计［J］.科技和产业，2014，14（2）：146-150.

［6］Yona A，Senjyu T，Saber A Y，et al，Application of neural networktoone-day-ahead24hoursgeneratingpower forecasting for photovoltaic system［J］.The 14th International Conference on Intelligent System Applications to Power Systems，2007，442-447.

［7］孙锐，汤义勤，马红伟，等，一种实用的超短期光伏发电预测方法［J］.电气技术，2013（1）：77-80.

［8］李鹏梅，臧传治，王侃侃，基于相似日和神经网络的光伏发电预测［J］.可再生能源，2013，31（10）：1-4.

［9］Su Y，Chan L C，Shu L J，Tsui K L，Real-time prediction models for output power and efficiency of grid-connected solar photovoltaic systems［J］.Applied Energy，2012（93）：319-326.

［10］Niu D X，Wei Y，Chen Y C，photovoltaic power prediction based on scene simulation knowledge mining and adaptive neural network［J］.Mathematical Problems in Engineering，2013（8）：206-232.

［11］陈昌松，段善旭，殷进军.基于神经网络的光伏阵列发电预测模型的设计［J］.电工技术学报，2009，24（9）：153-158.

［12］张艳霞，赵杰.基于反馈型神经网络的光伏系统发电功率预测［J］.电力系统保护与控制，2011，39（15）：96-101.

［13］康洪波，刘瑞梅，侯秀梅.基于神经网络光伏发电预测模型的研究［J］.电源技术，2013，37（3）：447-449.

［14］王增新，苏适，田沛.光伏发电预测技术的应用研究［J］.云南电力技术，2011，39（4）：27-30.

［15］吴雪莲，都洪基，基于BP神经网络-马尔科夫链的光伏发电预测［J］.电工电气，2014（3）：22-27.

［16］孙宏宇.基于DMC算法与遮蔽因子积分修正光伏发电预测研究［J］.硅谷，2012（13）：112-113.

The short-term photovoltaic power generation forecasting based on the fuzzy hyperbolic model

QI Hong-yun1，LUN Shu-xian2
（1.College of Engineering，Bohai University，Jinzhou 121013，China；2.College of New Energy，Bohai University，Jinzhou 121013，China）

Through the analysis and comparison of the factors that affect the generation of photovoltaic power generation，the short-term prediction model of photovoltaic power generation is established based on fuzzy hyperbolic model.This model is not only a kind of fuzzy model，but also a neural network model.Using its powerful learning ability，the historical data is used as the training sample.And get the stability of the model is used for short-term forecasting of photovoltaic power generation.Simulation results show that the prediction model has higher prediction accuracy compared with other prediction methods.

photovoltaic power generation；short-term forecasting；fuzzy hyperbolic model；prediction accuracy

TN302

A

1674－6236（2016）17-0001-03

2016-01-31稿件编号：201601300

国家自然科学基金项目（051501131）；教育部-新世纪优秀人才支持计划（NCET-11-1005）；2011年辽宁省第一批次科学计划项目（201402001）；辽宁省自然科学基金项目（2014020143）；辽宁省百千万人才工程项目（2012921061）

齐红云（1991—），女，山东泰安人，硕士研究生。研究方向：智能控制与滤波、光伏发电预测。