输入无模型动态扰动非线性系统的反演控制

张磊，李世雄，王哲，程春华

（1.海军航空工程学院a.科研部，山东烟台264001；b.青岛校区，山东青岛266041；2.海装装备采购中心，北京100071）

输入无模型动态扰动非线性系统的反演控制

张磊1a，李世雄2，王哲1b，程春华1b

（1.海军航空工程学院a.科研部，山东烟台264001；b.青岛校区，山东青岛266041；2.海装装备采购中心，北京100071）

研究了输入无模型动态扰动的不确定非线性系统的全局镇定。基于控制李雅普诺夫函数，设计了反演控制律，利用自抗扰的思想，构建扩展状态观测器来处理输入无模型动态，仿真结果验证了本方法的有效性。文章提出的控制方法适用于很多非线性系统。

输入无模型动态；不确定非线性；反演；扩展状态观测器

目前，鲁棒自适应理论和反演技术被广泛地应用于无模型动态的非线性系统的控制，并且取得了很多成果［1-4］。文献［5-7］针对线性输入无模型动态的系统展开了研究，提出了再设计方案，其结果被成功扩展到具有非线性输入无模型动态的系统的控制［8-10］。上述文献有些需限制为满足小增益，有些需假设无模型动态是严格无源的、零动态、最小相位等［11］。文献［12］针对输入非线性无模型动态的不确定非线性系统提出了基于再设计的动态缩放控制方案，但该方案稳定性分析复杂。文献［13］研究了具有输入未知动态的一阶电机系统，提出了鲁棒非线性PI控制，但很难扩展到高阶系统。文献［14-18］结合自抗扰思想和反演技术研究了非仿射非线性系统，实现了未知项和外来扰动的补偿。本文为解决非线性输入无模型动态系统的控制，引入自抗扰的思想，实现了该类问题的控制。

1　问题描述

考虑下面系统：

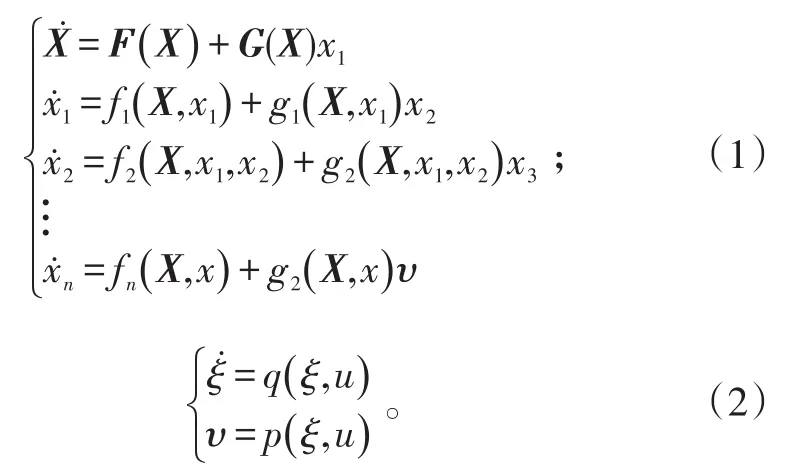
假设1：对于X子系统，可以将x1视为虚拟控制输入，则可选取控制李雅普诺夫函数V0（X）和虚拟控制，使得对所有的X≠0，满足：

式中，U0（X）是正定函数。

2　LGV-反演控制设计

反演设计开始前，假设已经为了X子系统设计好了V0（X）和虚拟控制。

将-η0LGV0（X）加入到，可得到虚拟控制律为：

式中，当η0＞0时，增加了LF+Gx1dV0（X）的负性。

定义误差变量e1=x1-x1d，则x2可视为（X，x1）子系统的虚拟控制输入，（X，x1）子系统如下：

Step 1：为了给（）X，x1子系统设计虚拟控制器，可以引入控制李雅普诺夫函数如下：

沿着式（5）、（6）微分得：

目标是设计x2d使得负定。又

则式（8）可写成

从而可以设计虚拟控制x2d为

式中，k1＞0是待设计的参数。

如果x2=x2d（X，x1），则有

之所以将该设计方法称之为LGV-反演，是因为通过设计了-η0LGV0（X）项在虚拟控制中，从而主导了式（8）中的符号不确定项。在抵消反演设计中，式（4）中的η0=0，即虚拟控制律，则在这步设计中，项必须要被抵消。结合LGV-反演和抵消反演，虚拟控制律可以设计为：

式（13）中：当λ1=1时为抵消反演设计；当λ1=0时为LGV-反演设计。

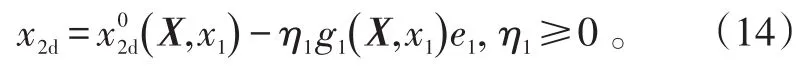
当i＜n时，可以设计虚拟控制律xi，d为：

定义变量ei+1=xi+1-xi+1，d。

Stepn：在最后控制律设计之前，引入自抗扰设计的思想，不妨将xn子系统分离为

则系统可扩展为：

式中，G（t）是未知项f（X，x，u）的导数，则可构建ESO：

式（20）中：E1是估计误差；Z1、Z2是观测器的状态；β01和β02是观测器增益（即待设计的参数）。函数fal（·）定义形式为［8-9］：

式（21）中：α1∈（0，1）；δ＞0。

构建控制李雅普诺夫函数如下：

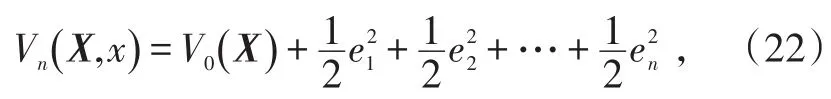
则控制律可选择为

式（23）中：kn＞1为待设计参数；Z2是扩展观测器的状态。

对Vn（X，x）求导可得：

根据文献［8-9］可以知道f（X，x，u）-Z2是个很小的值。综合上述设计过程，可以得出下面的定理。

定理1：由式（1）、（2）、（4）、（11）、（17）和控制律式（23）构成的闭环系统是稳定的，并且所有的闭环信号都是全局一致有界的。

证明：由上述设计过程可以看出，整个闭环系统是稳定的。由式（24），有：

求解式（25），可以得出：

当t→∞时，b（t）会趋近于一个非常小的值（由扩展状态观测器的设计决定了），同时eat→0，从而可以得出所有的闭环信号都是全局一致有界的。

3　仿真分析

考虑参考文献［6］中的对象，形式如下：

式中，η为未知输入动态。

在仿真过程中，初始值设置为：x（0）=［1，1，1］T，η（0）=0.5，Z1（0）=Z2（0）=0；观测器参数设置为：β01=100，β02=1 500，α1=0.25和δ=0.1；控制器参数设置为k1=k2=k3=5。仿真结果如图1～3所示。

图1　状态-时间曲线Fig.1 Time response of states

图2　控制律-时间曲线Fig.2 Time response of control law

图3　扩展状态观测器估计效果Fig.3 Effect of estimation by ESO

图1可以看出所有状态都收敛到0点附近。图2可以看出控制律是有界的。图3可以看出扩展状态观测器状态可以很好的估计未知项。

4　结论

本文针对一类具有输入无模型动态的非线性系统，提出了鲁棒反演控制。控制律设计中，直接在子系统n中引入了关于输入的未知非线性项，以替代无模型动态的影响。为了补偿这种替代，引入了自抗扰的思想，为其设计了扩展状态观测器。该设计方案简单易实现，通过稳定性分析以及仿真研究验证了该方案的有效性。

［1］POLYCARPOU M M，IOANNOU PA.A robust adaptive nonlinear control design［J］.Automatica，1996，32（3）：423-427.

［2］JIANG ZHONGPING，PRALY LAURENT.Design of ro-bust adaptive controllers for nonlinear systems with dynamic uncertainties［J］.Automatica，1998，34（7）：825-840.

［3］LIU YANJUN，TANG LI，TONG SHAOCHENG，et al. Adaptive NN controller design for a class of nonlinear MIMO discrete-time systems［J］.IEEE Transactions on Neural Networks and Learning Systems，2015，26（5）：1007-1018.

［4］KIM DOANG NGUYEN，HARRY DANKOWICZ. Adaptive control of underactuated robots with unmodeled dynamics［J］.Robotics and Autonomous Systems，2015，64（1）：84-99.

［5］KRSTIC M，JING SUN，KOKOTOVIC P.Robust control of nonlinear systems with input unmodeled dynamics［J］. Transactions on Automatic Control，1996，41（6）：913-920.

［6］JIANG Z P，MAREELS I，POMET J B.Controlling nonlinear systems with input unmodeled dynamics［C］//Proceedings of the 35thIEEE Conference on Decision and Control.Kobe，Japan：IEEE，1996：805-806.

［7］MURATARCAK，PETAR KOKOTOVIĆ.Robust nonlinear control of systems with input unmodeled dynamics［J］.Systems&Control Letters，2000，41（2）：115-122.

［8］MURAT ARCAK，MARIA SERON，JULIO BRASLAVSKY，et al.Robustification of backstepping against input unmodeled dynamics［J］.IEEE Transactions On Automatic Control，2000，45（7）：1358-1363.

［9］MURAT ARCAK，ANDREW TEEL，PETAR KOKOTOVIC.Robust nested saturation redesign for systems with input unmodeled dynamics［J］.IEEE Transactions on Automatic Control，1996，41（6）：913-920.

［10］CAIYUN WU，GEORGI M DIMIROVSKI，et al.Invariance control of a class of cascade nonlinear systems with input unmodeled dynamics［C］//ADynamic Systems and Control Conference.California，USA：ASME，2013：24-31.

［11］HU YUNAN，LI JING.Robust adaptive controller design for missile with three-tunnel input unmodeled dynamics and uncertainties［C］//Proceedings of 2010 Chinese Control and Decision Conference.Xuzhou：IEEE，2010：4016-4021.

［12］PRASHANTH KRISHNAMURTHY，FARSHAD KHORRAMI.A dynamic scaling based control redesign procedure for uncertain nonlinear systems with input unmodeled dynamics［C］//19thWorld Congress the International federation of automatic control.Cape Town，South Africa：IFAC，2014：3708-3713.

［13］HARIS E PSILLAKIS.Robustness of the nonlinear PI control method to ignored actuator dynamics［EB/OL］. https：//www.researchgate.net/publication/264790825.

［14］程春华，胡云安，吴进华.非仿射纯反馈非线性系统的自抗扰控制［J］.自动化学报，2014，40（7）：1528-1536. CHENG CHUNHUA，HU YUNAN，WU JINHUA.Auto disturbance controller of non-affine nonlinear pure feedback systems［J］.Acta Automatica Sinica，2014，40（7）：1528-1536.（in Chinese）

［15］程春华，胡云安，吴进华，等.非仿射系统的自适应观测器自抗扰控制［J］.控制理论与应用，2014，31（2）：148-158. CHENG CHUHUA，HU YUNAN，WU JINHUA，et al. Auto disturbance rejection controller for non-affine nonlinear systems with adaptive observers［J］.Control Theory &Applications，2014，31（2）：148-158.（in Chinese）

［16］程春华，胡云安，吴进华，等.输入非仿射不确定系统的跟踪控制［J］.系统工程与电子技术，2014，36（2）：354-360. CHENG CHUNHUA，HU YUNAN，WU JINHUA，et al. Track control of system with uncertainty and non-affine inputs［J］.Systems Engineering and Electronics，2014，36（2）：354-360.（in Chinese）

［17］胡云安，程春华，邹强，等.非仿射纯反馈系统的间接自适应神经网络控制［J］.控制理论与应用，2014，31（4）：467-478. HU YUNAN，CHENG CHUNHUA，ZOU QIANG，et al. Indirect adaptive neural networks controller for non-affine pure-feedback systems［J］.Control Theory&Applications，2014，31（4）：467-478.（in Chinese）

［18］程春华，吴进华，胡云安，等.受限的非仿射非线性系统的自适应控制［J］.控制理论与应用，2014，31（8）：1000-1008. CHENG CHUNHUA，WU JINHUA，HU YUNAN，et al. Adaptive control of non-affine nonlinear system with saturation constraint［J］.Control Theory&Applications，2014，31（8）：1000-1008.（in Chinese）

Backstepping control for Uncertain Nonlinear Systems with Input Unmodeled Dynamics

ZHANG Lei1a，LI Shixiong2，WANG Zhe1b，CHENG Chunhua1b
（1.Naval Aeronautical and Astronautical University a.Department of Scientific Research，Yantai Shandong 264001；b.Qingdao Branch，Qingdao Shandong 266041，China；2.Outfit Purchasing Centre of NED，Beijing 100071，China）

The global asymptotic stabilization problem for a general class of uncertain nonlinear systems with dynamic input uncertainties（input unmodeled dynamics）was considered.A backstepping control law was constructed from a control Lyapunov function（CLF）.In the control scheme，extend state observer based on active disturbance rejection ideal was designed to deal with the input unmodeled dynamics.The proposed control method was applicable to a wide class of nonlinear systems，meanwhile，the simulation result was presented to illustrate the effectiveness of the proposed control scheme.

input unmodeled dynamics；uncertain nonlinear；backstepping；extend state observer

TP273

A

1673-1522（2016）03-0337-04DOI:10.7682/j.issn.1673-1522.2016.03.007

2016-03-15；

2016-04-20

张磊（1979-），男，工程师，博士。