数学教学中关于学生主动参与的几点看法
2016-10-21洪锦飞
洪锦飞

数学新课程标准不仅强调基础知识与基本技能的获得,更强调让学生经历数学知识的形成过程,了解数学的价值,增强运用数学的意识,充分发展学生的情感态度和一般能力。因此,要实现数学新课程标准,教学中学生的主动参与则显得非常重要,这里指的学生的主动参与有别于过去的传统教学中单纯的知识授受和教师主导,而更强调学生带着兴趣和欲望去寻求知识、方法、技巧去解决问题,自主地参与获得知识的过程。本文将谈谈数学教学中如何促使学生主动参与的几点看法:
一、创设生活中的数学情境,激发学生主动参与的兴趣
过去,数学的教学内容都是极抽象的数学概念、公式、定理等,更没有把数学和生活实际联系起来,学生不能在数学学习中感受到乐趣,对数学的看法就是“难”“枯燥”“无用”,试问这样的数学又怎能引起学生主动参与的兴趣呢?建构主义流派一致认为,知识的获得不是外部灌输的,而是主体自己建构的,学习的过程同时也是学习者依据自身的经验从而建构新经验的过程,教学活动要让学习者参与到其中来,教学过程要注重创设情境和纳入真实性任务。所以,数学教学中应创设恰当的情境,给学生展示生活中有趣的、有意义的、实际的数学,激发学生主动参与的兴趣。
例1.距离问题的情境设置(水电站建在哪里好?)
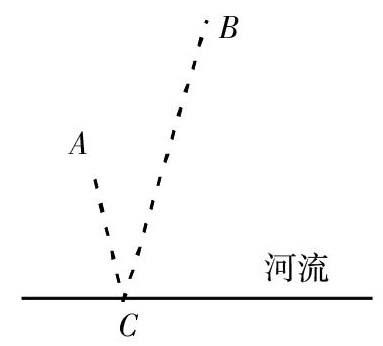
某河流的同侧有两个村庄,A村、B村(如左图),两村计划于河上共建一水电站发电供两村使用,已知A村、B村到河边的垂直距离分别是300 m、700 m,两村相距500 m,河流的弯度可忽略。为了使送电到两村的电线用料最省,水电站建于何处最佳?为什么?
这是一道较简单的联系实际的工程问题的数学题,给学生展示的是有用的数学,学生想学的正是这种在生活中可以用得上的数学。教师不把最简便的方法告诉学生,而是鼓励学生想出各种不同的方法,这样更有利于提高学生参与的主动性。
例2. 概率问题的情境设置(一定能摸到红球吗?)
针对社会上特别是农村的家长赌“六合彩”这一现象,我是这样设计问题情境的:
师:同学们,“六合彩”這一名词我相信对大家来说并不陌生,甚至有很多家长都“积极参与”,你们认为“六合彩”真的能盈利?(全班学生情绪高涨,议论纷纷。)
生:应该能盈利,赔率是1∶40啊!例如中了100元就有4000元。(大部分学生都表示赞同)
师:从你们身边事例去分析,究竟是中奖的人多还是没有中奖的人多?那些参与“六合彩”的人现在的生活状况又是怎样?(现实中很多人因为“六合彩”,出现了不务正业,逃债、躲债,甚至妻离子散,家破人亡的现象。)
生:没有中奖的人多。
师:“六合彩”绝对是稳输没赢!(同学们都用求知若渴的眼神望着我,都急切地等待老师的解答。)同学们,“六合彩”中奖可以用数学中的“概率”知识去解答。如果我们学习了这一节“一定能摸到红球吗?”的内容,不用老师为你们解释,你自己就能知道为什么了。
通过这样的问题情境教学,学生都能积极地投入到学习中,让更多的学生参与本节教学,并对学生进行了思想道德教育,使其明辨是非对错,最终达到了教学效果。
二、学生参与数学概念的建立过程,挖掘数学性质
数学概念的形成过程一般来自于解决实际问题或教学自身发展的需要,而教材上的定义常常隐去概念形成的思维过程,所以,教师在进行概念教学时,要引导学生参与数学概念的建立过程,使学生弄清概念的来龙去脉,加深对概念的理解,从而准确把握概念的实质。通过揭示概念中的每一词、句的真实含义,抓住概念的本质特征,阐明概念间的内在联系,注意概念的比较,归纳、区分概念的异同等方法,使学生共同参与数学概念的建立过程,挖掘数学的性质。
例如,讲授函数概念时,为了使学生更好地理解掌握函数概念,我们必须揭示其本质特征,进行剖析:(1)“存在某个变化过程”——说明变量的存在性;(2)“在某个变化过程中有两个变量x和y”——说明函数是研究两个变量之间的依存关系;(3)“对于x在某一个范围内的每一个确定的值”——说明变量x的取值是有范围限制的,即允许值范围;(4)“y有唯一确定的值和它对应”——说明有唯一确定的对应规律。由以上剖析可知,函数概念的本质是对应关系。
三、实施师生共同探索、研究,学生自主参与为主的教学,引导学生自主解决探索过程中的问题
探究性学习与研究性学习的主要意思是:询问,打听;调查,探究。对探究学习,美国学者一般使用施瓦布的定义:学生自主地参与获得知识的过程,掌握研究自然所必需的探究能力;同时,形成认识自然的基础——科学概念;进而培养探索未知世界的积极态度。这里强调的是“自主地参与获得知识的过程”,同时形成科学概念和探究能力。数学课程教学中突出探究教学,可使学生在数学基础知识、基本技能的学习过程中,积极主动参与,有效地培养学生勇于质疑和善于反思的习惯,培养学生发现、提出、解决问题的能力,亲身体验数学发现和创造的历程。
例,教学“字母能表示什么”时,课前先让学生准备足够多的火柴棒,分小组在课堂上动手实践探究:
问:搭1个正方形需要4根火柴棒,搭2个正方形需要 根,搭3个正方形需要 根,搭n个正方形需要 根。
分析:鼓励学生充分从正方形的构造特点去分析所用的火柴棒数,可用以下多种思路等:
①把第一个正方形看成有4根,然后每多搭1个正方形多3根,多搭了(n-1)个正方形,因此,列式为:4+3(n-1) = 3n+1
②搭n个正方形可以看成由第一根火柴棒再加n个3n根火柴棒组成,因此,列式为:1+3n=3n+1
③搭n个正方形可以看成上下横放的火柴棒有2n根,竖放的火柴棒有(n+1)根,因此,列式为:2n+(n+1)= 3n+1
④ 搭n个正方形可以看成每搭一个长方形需要4根,从第二个正方形开始,(n-1)个正方形都多算了1根,因此,列式为:4n-(n-1)。
四、通过开放题、小组讨论,有效促使学生自主探索、合作交流
数学学习是学生自己的活动过程,学生通过自己的活动建立对人类已有的数学知识的理解,数学教学是数学活动的教学,数学学习不是单纯的知识接受,而是以学生为主体的数学活动。数学开放题是相对于条件完备、结论确定的传统封闭题而言,是指那些条件不完备,解题策略多样,结论不确定的数学问题。在开放题教学中,教师让学生感受新知,主动探究新知,自主解决新知,师生共同讨论、质疑、评价,开放题能更好地让教师对学生开放,多组织学生质疑,让新知对学生开放,多让学生自主探究解答。
例如,张大伯家院子里有一个长4米,宽2米,(如下图)用栅栏围成的长方形羊圈,他买来20只羊,可是羊圈嫌小,因为每只羊占地面积大约1平方米,怎么办?你能帮张大伯出个主意吗?
学生经过思考、动笔验算起来,各自说出自己的主意。教师组织学生先在小组内交流后大组汇报。在提交结论时,教师层层引入,可以怎样围?围成什么形状?
①不靠墙时,长方形、正方形、圆的面积。
②一边靠墙时,长方形、正方形、半圆的面积。
③大胆猜想:既然一边靠墙,那么就可以两边靠墙,计算更大的羊圈面积。
此题教学中,自始至终学生都是学习的主人,而教师只是学生学习的组织者、帮助者、合作者。教师在设计、安排和组织教学过程中都充分地让学生有自主探索、合作交流、積极思考的空间和机会,在自主探索、合作交流的氛围中,解除困惑,更清楚地明确自己的思想。
五、把数学建模引入教学中,发挥学生的参与意识,体现学生主体性
学数学不如做数学。数学建模,是指从研究一个真实世界的具体现象或问题开始,试图把它数学化的过程。据现代建构主义学习观,知识不能简单地由教师或其他人传授给学生,而只能由学生依据自身已有的知识和经验主动地加以建构。强化数学建模的教学,可极大地改变传统的教学法,它一改过去满堂灌模式为讨论班方式,教师扮演的是教学的设计者和指导者,学生是学习过程中的主体,师生处于平等地位。由于要求学生对学习的内容进行报告、答辩或争辩,因此,极大地调动了学生自觉学习、主动参与的积极性。
参考文献:
曹一鸣.数学教学模式的重构与超越[D].南京师范大学,2003.
