高校火车临时售票窗口排队问题分析

蔡秋娥　甘东

摘 要：售票窗口的排队问题在生活中到处可见，为提高系统效率，文章以我校火车票临时售票窗口排队问题为例，基于泊松分布和排队论分析和确定所需的售票窗口数，理论计算结果和实际情况相比较，得出学校火车临时售票窗口数目的最优结果。

关键词：泊松过程；排队论；售票窗口数；最优化

现代交通业越来越发达，但是同时也衍生了很多的问题，而排队买票就是其中一个比较突出的问题。文章以我校火车票临时售票窗口排队问题为例，基于泊松分布和排队论分析和确定所需的售票窗口数，理论计算结果和实际情况相比较，得出学校火车临时售票窗口数目的最优结果，為减少购票者的等待时间、 提高服务台服务与管理水平提供理论依据。

1 排队论系统理论及模型建立

1.1 排队论系统理论名词及符号解释

用排队论来研究排队服务系统，首先要对各种排队系统进行分类描述。任何排队服务系统都可以描述为以下四个方面。

学校临时售票窗口排队问题属于并列多服务台单队排队系统，一般用模型M/M/s表示。此模型学生到达临时售票窗口过程近似服从泊松分布，窗口服务时间近似服从指数分布共有s个服务窗口。

1.2 M/M/s模型概述

如果我们把细胞的分裂看成是顾客的到达，细胞死亡看成是服务完毕顾客的离去，X（t）表示t时间顾客的数目，则{x（t），t？叟0}就可以看作是一个生灭的过程。在多服务台的等待制排队系统中，我们有以下定理：

引理1.2.1：若X（t）表示时刻t系统中的顾客数，则{x（t），t？叟0}是状态空间E={0，1，2}且生率为：？姿k=？姿，k=0，1，2，...，灭率为：？滋kk？滋，k=0，1，2，...nn？滋，k=n+1的生灭过程。

评价一个排队系统的好坏要以顾客与服务机构两方面的利益为标准。顾客与服务机构为了照顾自己的利益对排队系统中的三个指标：队长、等待时间、服务台的忙期（简称忙期）都很关心。因此这三个指标也就成了排队论的主要研究内容。

2 基于泊松分布和排队论的火车临时售票窗口排队问题分析

2.1 数据处理

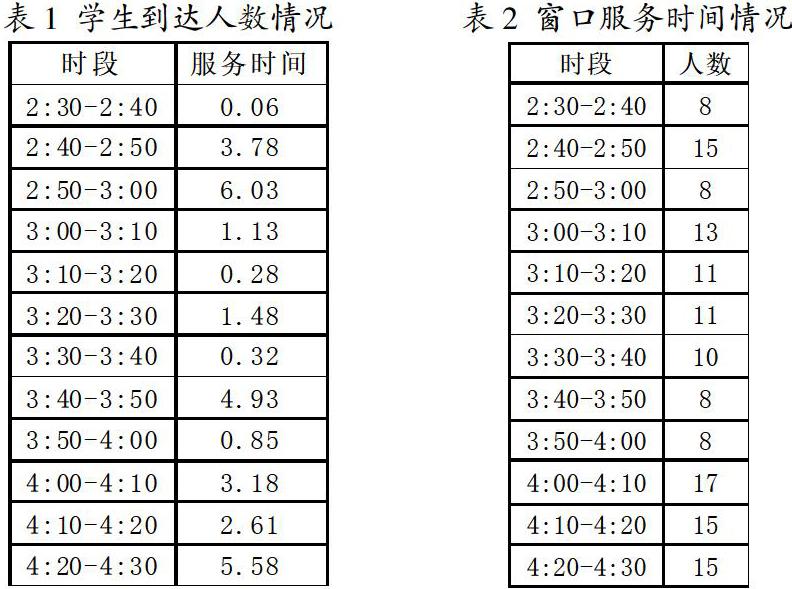
以南华大学火车票临时售票窗口为研究对象，我们进行了多次的实地调查并统计了结果，在此我们选取了其中一天下午2点30分到4点30分内所到达的学生到达情况与窗口服务情况，得到样本数据如表1、表2所示。

2.2 学生流量分析和窗口服务人数分析

根据表1的统计结果，通过SPSS20.0统计软件进行单样本Kolmogorov-Smirnov检验，检验结果如表3所示。

如表3所示渐近显著性（双侧）P=0.952>0.05，可以认为学生到达临时售票窗口过程近似服从泊松分布。学生到达平均速率？姿=11.5833≈12（人/10分钟）=1.2（人/分钟）。

同理可根据表2的统计结果，通过SPSS20.0统计软件进行单样本Kolmogorov-Smirnov检验，检验结果如表4所示。

如表4所示渐近显著性（双侧）P=0.962>0.05，可以认为窗口服务时间近似服从指数分布。窗口平均服务速度？滋=0.397（人/分钟）。

2.3 指标计算

通过上述增加临时窗口数量的方法可知，增加1个临时售票窗口，可使学生的平均逗留时间减少1.02分钟，可一定程度上减缓排队等待问题，再增加1个临时售票窗口，可使学生的平均逗留时间减少0.22分钟，表明继续增加售票窗口，则无法使得问题得到进一步的改善。需要从售票员工的职业素质等方面进行提升，以获得更好的结果。

3 结果及最优化

综上，在当前所分析的时间段中，当临时售票窗口数目为5时，学生与售票点的费用到达最优化水平。该结论与学校周围售票窗口现状基本符合。

参考文献

[1]胡细宝，王丽霞.概率论与数理统计[M].北京邮电大学出版社，2004.

[2]王东升，刘玉堂.泊松过程在排队论中的应用[J].河南机电高等专科学校学报，2007（2）：121-125.

[3]杨劲峰.校图书馆经费的合理利用[J].现代经济信息，2009（3）：89-137.

[4]沈留印，闫秀霞.排队论在商场收货区优化中的应用[J].山东理工大学学报，2011：78-81.

[5]白竹.基于排队论的公交站台线路容量优化研究[J].黑龙江工程学院学报，2012：67-70.

[6]高显彩.排队论在银行排队系统中的应用[J].宿州教育学院学报，2013（3）：108-111.

作者简介：蔡秋娥（1980-），女，湖南攸县人，在读博士，现工作于南华大学数理学院，讲师，研究方向为概率论与数理统计的应用。