基于量子差分进化优化LSSVM的短期负荷预测

刘仕豪

【摘 要】为了提高短期负荷预测的精度，提出基于量子差分进化算法（quantum differential evolution，QDE）优化的最小二乘支持向量机（least squares-support vector machine，LSSVM）模型。通过采用量子比特编码方案有效选取最小二乘支持向量机的参数，克服了最小二乘支持向量机算法中依据经验选定参数的盲目性。实例验证结果表明，与BP神经网路和单纯的最小二乘支持向量机算法相比，QDE-LSSVM有更高的预测精度，更适用于当前中国短期负荷的需要。

【关键词】短期负荷预测；参数优化；量子差分进化；最小二乘支持向量机

引言

“十三五”规划期间，随着电力市场化改革的进一步深化与智能电网的大规模试点，精度较高的负荷预测对保障智能电网的安全稳定运行与电能资源的优化配置至关重要。故不断改进负荷预测方法，提高预测的精度，对于制定经济优化的发电计划、降低旋转储备容量、进行电力市场需求分析等方面均有十分重要的意义。

目前，用于负荷预测的方法大体可以分为经典的数学统计方法和基于人工智能的方法，其中，大多数负荷预测理论都基于时间序列分析，包括自回归模型（VAR）[1]，自回归滑动平均模型（ARMA）模型[2]等，时间序列平滑预测法的模型识别与参数估计都是根据有限序列去推断原序列式的性质来完成，这种推断误差较大，不能满足短期负荷预测精度需要。随着世界各国电力市场的发展，负荷预测受到了更加广泛的重视，神经网络预测技术[3]，混沌預测技术[4]以及粒子群优化[5]，LSSVM[6]等自学能力较强的预测方法都在负荷预测中应用广泛。负荷预测是ANN在电力系统应用中最合适的领域，但由于神经网络模型输入的原始数据必须以精准为前提，而实际预测时，因统计存在差异，使得数据同实际值有一定差别，导致预测精度不理想。并且针对不同地区的特点，应根据其负荷变化的规律及气象变化规律选取不同的特征参数，不同的ANN模型与结构，这就增加了推广的难度。

与神经网络算法采用经验风险最小化原则不同，支持向量机（SVM）采用的是结构风险最小化原则，将求解过程转化为凸二次规划问题。这就很好地克服了神经网络的一些不足，且在负荷预测的实际应用中取得了很好地性能表现。但是正则化参数与核参数的选择极大影响着LSSVM的性能。量子差分进化算法有效的克服了群智能算法中比较普遍的早熟现象，提高了全局的搜索能力。本文通过量子差分进化算法优化最小二乘支持向量机模型的正则化参数与核函数参数，实现参数的自动调整。

一、基于量子差分进化的LSSVM建模过程

在基于量子差分进化的LSSVM建模中，LSSVM输出值为带有和的因变量，而正则参数与核函数由量子差分进化算法进行优化选取，优化的目标函数为输出值与实际值的误差平方和。

优化目标函数定义为：

其中，yi为第个已知样本的输入值，yi'为第个样本对应的模型预测输出值，为样本总体个数。

则基于QDE的LSSVM模型参数的组合寻优步骤如下：

1）参数初始化

QDE算法的主要参数为种群规模N，染色体长度D，变异因子F，交叉因子C和最大世代数g，其中，g初始化为0。

2）种群初始化

产生一个N*D规模均匀分布的随机数矩阵，按照以下方式：

其中，i=1，2，……，N，j=1，2，……，D，与分别表示第j列的上界和下界。

3） 量子编码

对初始种群进行量子编码

4） 变异操作

变异操作使用两个随机向量，按照公产生变异向量

5）交叉操作

交叉操作可以增加种群多样性

6）选择操作

选择操作保证更优的后代生存到下一个世代，选择操作的原则是按照最优适应度进行。

综上，基于QDE改进的LSSVM算法流程图如图1所示。

二、算例分析

本文选取山西阳泉2013-5-01至2013-5-31全天24个小时的历史预测数据，影响因素包括：日分类，0表示样本日为工作日（周一—周五），0.8表示一般休息日（周六、周天），1表示节假日（法定节假日与民间节日）；日温度（日最高温度，日最低温度）；日降水量。选取2013-5-01至2013-5-30的720个数据作为训练样本，2013-5-31作为测试样本。同时，为了反映不同的负荷情况，31号得到了24个小时的测试结果。

为了准确评估预测模型，采用平均绝对百分比误差与最大相对误差来衡量模型预测结果的可行性。

其中，与分别为测试样本的输出值与实际数值。

设定种群规模，变异概率Pm=0.05，交叉因子Cr=0.5，收缩因子且随机生成种群数。根据图1所示流程，对2013-5-31进行24点负荷预测。

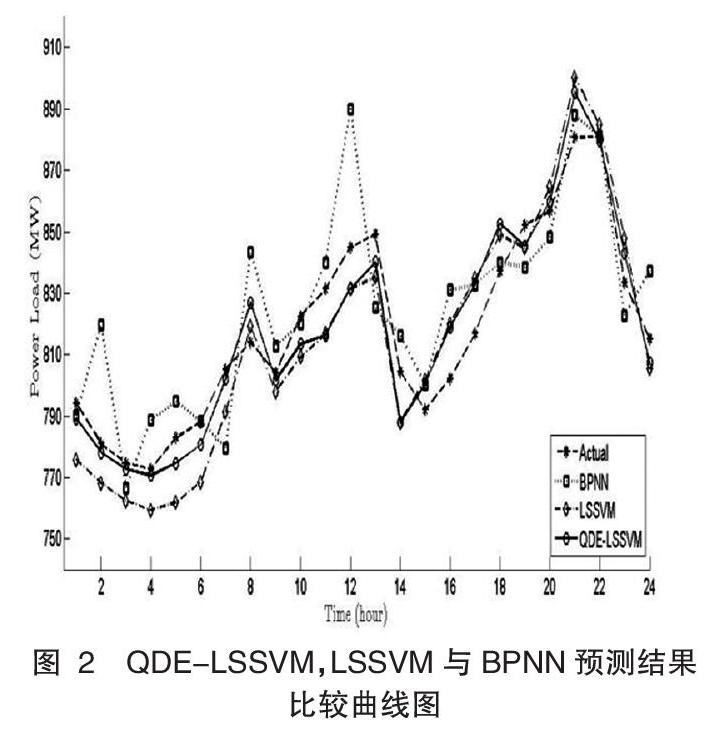
从图2中可以看到，短期负荷量与时间成非线性相关。因此，将LSSVM预测及BPNN的预测结果作为对比。LSSVM的预测步骤与QDE_LSSVM的预测步骤相似，未经过QDE优化的LSSVM的参数为（？酌，？滓2）=（0.4641.725），BPNN网络的网络结构为2-5-1， BPNN网络的迭代次数设定为1000，学习率为0.5，目标为0.00004。

图2给出了QDE_LSSVM，LSSVM与BPNN的短期负荷预测结果。其中BPNN的预测值波动性较大，不能满足短期负荷预测要求的稳定性原则。而经过改进的LSSVM模型更加接近原始曲线，能够满足实际电力系统负荷预测的要求。

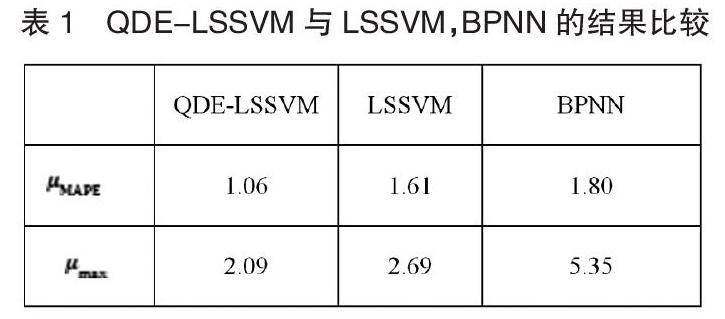
表1给出了三种预测方法的平均相对误差与最大相对误差，其中QDE_LSSVM的平均相对误差最低，为1.06%，比BPNN低0.74%。这表明，与BPNN相比，QDE_LSSVM的小样本集合回归问题上具有显著优势。原因是LSSVM满足结构风险最小化原则，具有较强的推广能力，可以避免ANN法对训练样本数量和质量要求的较高不足。QDE-LSSVM的平均相对误差比LSSVM低0.55%，这表明QDE-LSSVM的预测效率要优于LSSVM。

结论

考虑电力负荷的历史数据，日期类型以及气象因素，本文利用QDE_LSSVM法进行短期负荷预测。从实验效果来看，可以得到以下结论：

1）根据确定LSSVM参数存在的问题，引入QDE对参数进行优化。实验结果表明提出的方法能够自动提取识别率高且收敛速度较快的参数。

2）提出了应用QDE-LSSVM法进行短期负荷预测。实验结果表明，与BPNN和LSSVM法相比，QDE-LSSVM算法能够实现较高的预测精度，验证了所构建模型的正确性和有效性。作为一种启发式混合算法，本文所提出的方法能够为智能电网制定科学合理的发电计划提供一定的依据。

参考文献：

[1]万昆，柳瑞禹.区间时间序列向量自回归模型在短期电力负荷预测中的应用[J].电网技术，2012，11：77-81.

[2]黄元生，邓佳佳，苑珍珍.基于ARMA误差修正和自适应粒子群优化的SVM短期负荷预测[J].电力系统保护与控制，2011，14：26-32.

[3]代林.基于神经网络的电力负荷预测方法研究及实现[D].电子科技大学，2012.

[4]杨红英，叶昊，王桂增.混沌理论在电力系统负荷预测中的应用[J].继电器，2005，16：26-30.