软化静力推覆曲线的分段线性拟合

向　畅，彭　军，苏　亮

浙江大学建筑工程学院，浙江杭州 310058



【土木建筑工程 / Architecture and Civil Engineering】

软化静力推覆曲线的分段线性拟合

向畅，彭军，苏亮

浙江大学建筑工程学院，浙江杭州 310058

由于传统的双线性方法无法准确拟合软化的静力推覆曲线，基于等能量原则，提出一种软化静力推覆曲线的三线性分段拟合方法，并给出等效过程的具体步骤. 以2个钢筋混凝土框架结构为算例，对软化的静力推覆曲线分别进行双线性和三线性等效，并与原结构非线性动力时程分析的结果进行比较. 结果表明，对于软化的静力推覆曲线，三线性等效方法比双线性等效方法更接近非线性动力时程分析的结果.

结构工程；推覆分析；推覆曲线；双线性拟合；三线性拟合；非线性时程分析

静力推覆分析方法具有精度较高和时耗较小等优点，是建筑结构基于性能的抗震设计和性能评估的常用方法．此方法主要步骤包括：

1)在某种侧向力模式下对多自由度结构实施推覆分析，得到基底剪力-顶点位移曲线；

2)将基底剪力-顶点位移曲线理想化为等效单自由体系的能力曲线， 得到周期、 骨架曲线等参数；

3)根据等效单自由度体系的能力曲线、周期和阻尼等参数，通过非线性时程分析或者弹塑性反应谱[1-2]计算得到单自由度体系的峰值反应；

4)将等效单自由度体系的峰值反应转换为多自由度结构的峰值反应(通常为顶点位移峰值)；

5)比较结构能力和定义的需求，对结构性能做出评估．

静力推覆分析方法没有严格的理论基础，在实施的每一步都引入了一些假设．自该方法提出至今，已有大批学者对其进行了改进以提高其分析精度．如Chopra等[3-5]根据结构动力学理论，提出考虑高阶振型影响的模态推覆分析方法；Gupta等[6]考虑侧向力模式的变化提出适应力分析方法；Antoniou等[7-8]比较了适应力和非适应力模式的优缺点并提出基于位移的适应谱分析方法；Kalkan等[9]采用适应分析算法，提出考虑高阶振型的适应模态组合方法；毛建猛等[10]考虑结构屈服后地震作用发生变化特性，提出两阶段模态推覆分析方法；Poursha等[11-13]使用多阶段和一阶段的推覆分析，提出连贯模态推覆分析方法；杨红等[14-15]使用结构处于较大非线性时的模态参数替代原始模态推覆分析的弹性模态参数，提升了精度．现有的关于静力推覆分析及改进的研究，主要是对其侧向力模式的改进和考虑高阶振型的影响两个方面，而对于如何准确将多自由度结构推覆曲线拟合为单自由度体系能力曲线的研究则相对较少．

传统方法主要采用双线性将多自由度结构的推覆曲线拟合为单自由度体系的能力曲线，该拟合方法对屈服后硬化的静力推覆曲线具有很好的近似性和适用性，但对于屈服后软化的静力推覆曲线，该拟合方法不能准确地拟合原结构推覆曲线．为此，本研究提出三线性分段等能量方法来拟合原推覆曲线，并采用2个算例验证了该方法的准确性和适用性．

1　三线性拟合方法

本研究以模态推覆分析为例来介绍提出的方法.图1(a)中的曲线为n阶模态推覆分析的基底剪力-顶点位移曲线，传统的方法使用两折线来拟合这一曲线，两段折线与坐标轴所围面积与原曲线与坐标轴所围面积相等，再利用式(1)将两折线转化为单自由度体系的力-位移曲线，如图1(b)．单自由度体系的屈服力和屈服位移存在式(2)所示的关系.

(1)

(2)

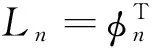
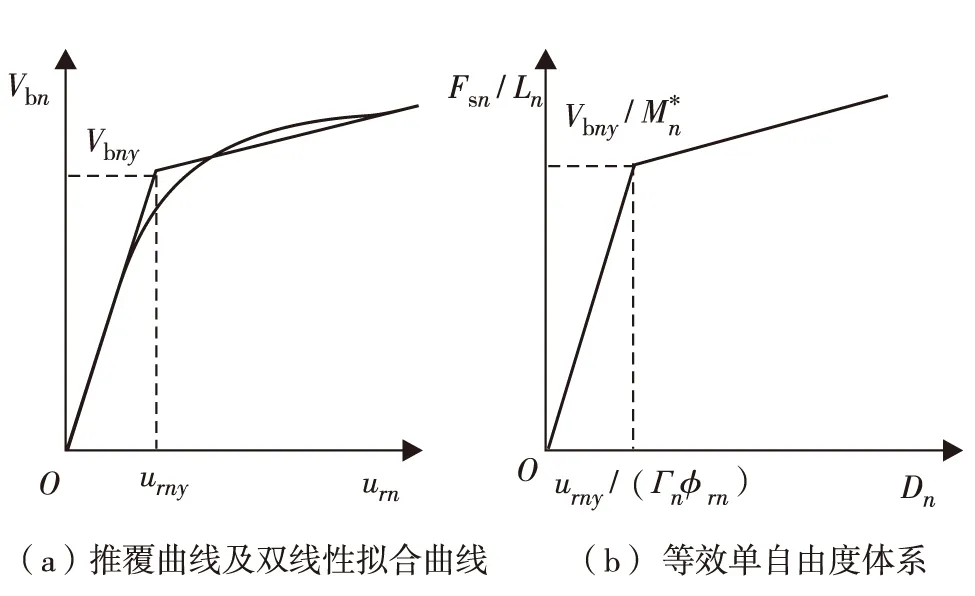
图1　第n阶模态推覆曲线及其等效单自由体系参数Fig.1 Pushover curve and equivalent SDOF parameters of the n-th mode

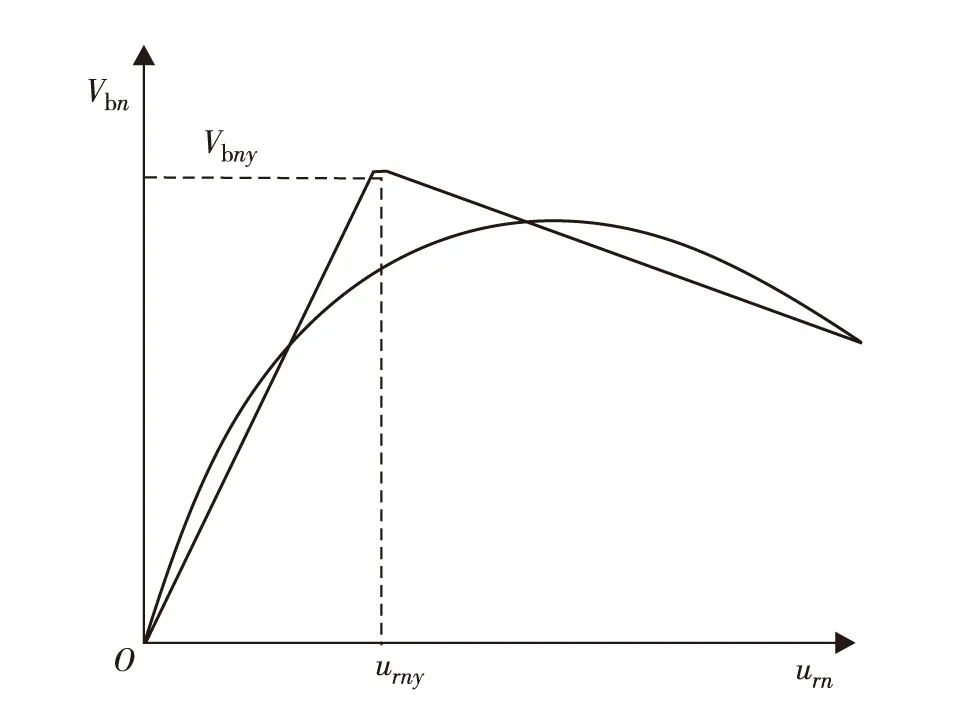
图2　软化的推覆曲线及其双线性拟合曲线Fig.2　Softening pushover curve and its bilinear fitting curve

然而对于屈服后软化的静力推覆曲线，如图2所示，若采用双线性拟合方法，则会高估单自由度体系的峰值反应，拟合的曲线与原曲线差异较大. 采用三线性拟合方法，如图3，在拟合上更接近于原推覆曲线．基于对结构的倒塌模拟分析，文献[16-17]分别提出了2种三线性拟合方法，需要指出的是，这2种方法主要应用于结构的倒塌模拟分析，对一般的静力弹塑性分析，不具有普适性. 参考这2种方法，本研究提出了在静力弹塑性分析中结构软化推覆曲线的三线性拟合方法．等能量原则在能力曲线的拟合中被认为是一种基本原则，因此本研究也采用分段等能量原则对原推覆曲线进行拟合，其详细拟合步骤为：

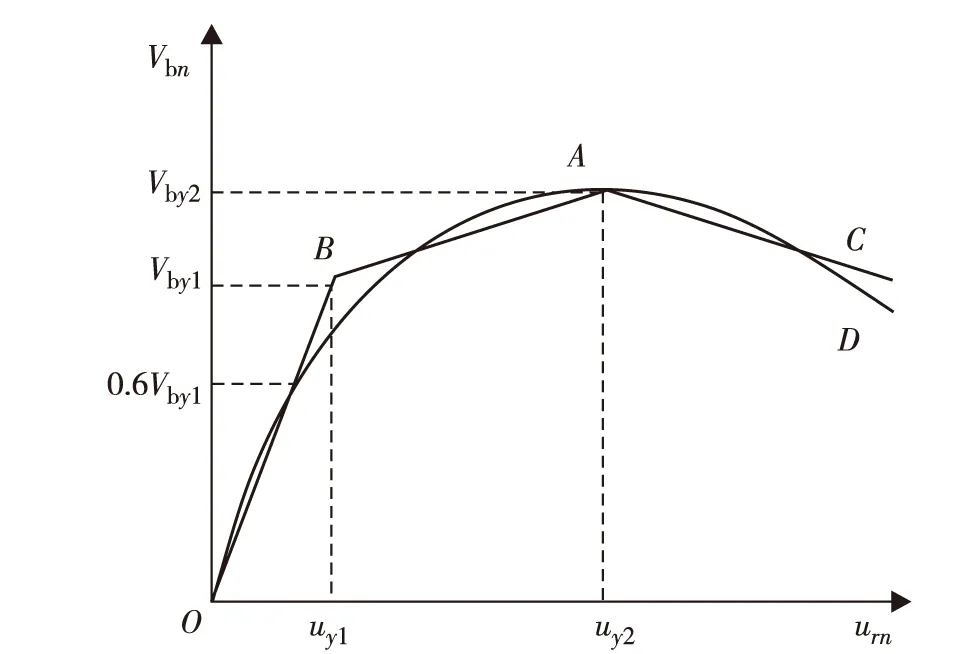
图3　软化的推覆曲线及三线性拟合曲线Fig.3　Softening pushover curve and its trilinear fitting curve

1)找出推覆曲线上基底剪力最大点A， 如图3所示，计算出该点与原点之间的曲线与坐标轴所包围的面积S1；

2)估计屈服基底剪力Vby1， 取60% Vby1处的割线刚度作为有效初始刚度K， 并计算Vby1对应点的屈服位移uy1=Vby1/K；

3)连接原点、屈服剪力Vby1对应的B点和A点， 计算此折线与坐标轴所包围的面积S2；

4)计算误差(S2-S1)/S1；

6)找出原推覆曲线上最末端点D， 计算点D与点A之间曲线与坐标轴所围面积记为S3；

7)三线性拟合曲线的最末端点记为C， C点横坐标与D点横坐标相同， 估计C点纵坐标Vcy， 并计算直线AC与横坐标轴所围面积S4；

8)计算误差(S4-S3)/S3；

10)利用式(1)把三线性曲线转化为单自由度体系的力-位移曲线，如图4所示．

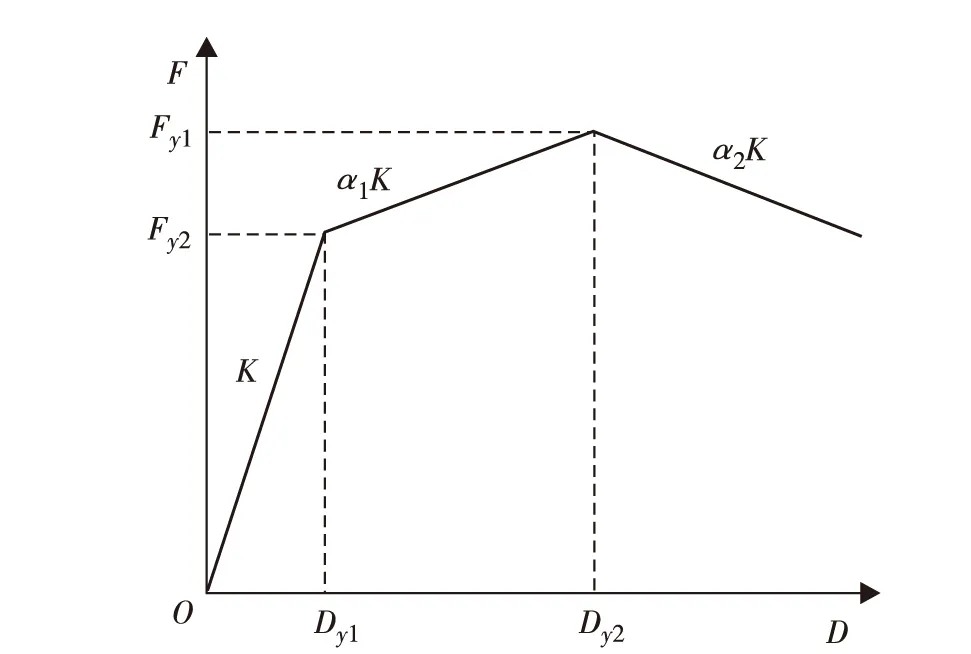
图4　三线性拟合方法等效单自由度体系Fig.4　Equivalent single degree of freedom with trilinear fitting method

2　算　例

2.1分析步骤

采用两个算例来验证所提出的三线性拟合方法的精确性．为简便分析，静力弹塑性分析方法采用模态推覆分析．关于推覆分析的侧向力模式选取有许多研究文献，本研究只是为了说明三线性拟合方法相对于传统方法的准确性，不去深入探讨各种侧向力模式分析结果的差异. 计算分析时，单自由度体系不考虑其在往复力作用下强度与刚度的退化，滞回模型采用完全弹塑性模型，计算步骤如下：

1)对结构进行模态分析，得到结构弹性自振周期和振型；

2)对结构分别进行各阶模态推覆分析(本研究只取前3阶)，得到各阶模态相应的基底剪力-顶点位移曲线；

3)分别把各阶基底剪力-顶点位移曲线简化为双线性和三线性曲线， 并转化为单自由度体系的力-位移关系曲线，若高阶模态的推覆曲线不具有软化段，则进行双线性拟合；

4)对等效单自由度体系给定的力-位移关系折线、周期和阻尼比(5%)，计算各阶单自由度体系峰值变形，这一步可以通过弹塑性设计谱或者非线性动力时程分析，为了便于与原多自由度结构非线性动力时程分析结果进行比较，单自由度体系峰值变形的计算采用非线性动力时程分析；

5)分别将各阶模态等效单自由度体系的非线性动力时程分析结果求取平均值，并将各阶模态的平均值进行平方和开平方组合，求出原结构在实际地震动下的顶点位移；

6)分别找出各阶模态推覆分析数据库中相应于第5)步单自由度体系非线性动力时程峰值变形处的楼层位移和层间位移角，并进行平方和开平方组合；

7)对原多自由度结构在相同的地震动记录下进行非线性动力时程分析；

8)分别比较双线性拟合和三线性拟合方法计算结果与原结构非线性时程计算结果差异．

本研究的天然地震动记录均来自于太平洋地震工程研究中心强震数据库[19].需要说明的是，由于相同的地震波分别输入到等效单自由度体系和原多自由度结构中进行计算，地震动记录之间的离散性对等效单自由度体系和原多自由度结构的计算结果都会产生影响，因此不会对结果之间的比较产生实质性的影响．但为了使得计算结果离散性不至于太大，采取常用的双频段选波方法[20]对地震波进行筛选，算例Ⅰ和算例Ⅱ均选择了20条地震波，分别如表1和表2所示，为了使结构充分进入到非线性阶段，将各条波的峰值加速度均调整到0.4g， g为重力加速度．

2.2算例Ⅰ

算例Ⅰ模型见图5，为一个6层单榀框架结构，设防烈度为8度0.2g， 柱尺寸500 mm×500 mm，梁尺寸300 mm×500 mm；混凝土强度等级柱、梁均为C30．梁柱主筋均为HRB335级，箍筋HPB235级．在OpenSees平台上建立模型，模态推覆分析和非线性时程分析均在该平台上完成．建模时混凝土模型采用Concrete02模型，钢筋模型采用Steel02模型，为了考虑箍筋对其包围混凝土的轴心抗压强度和极限应变的影响，把混凝土材料分为约束混凝土区和非约束混凝土区，分别按照混凝土结构设计规范[21]的要求取平均值．梁、柱截面采用纤维截面模型，该模型可以分别定义混凝土纤维和钢筋纤维，把混凝土划分为多个网格，每根纵向钢筋视为一根纤维，截面依据平截面假定确定应变．梁、柱单元选用基于位移的非线性纤维梁柱单元，每根梁、柱构件划分为6个单元．

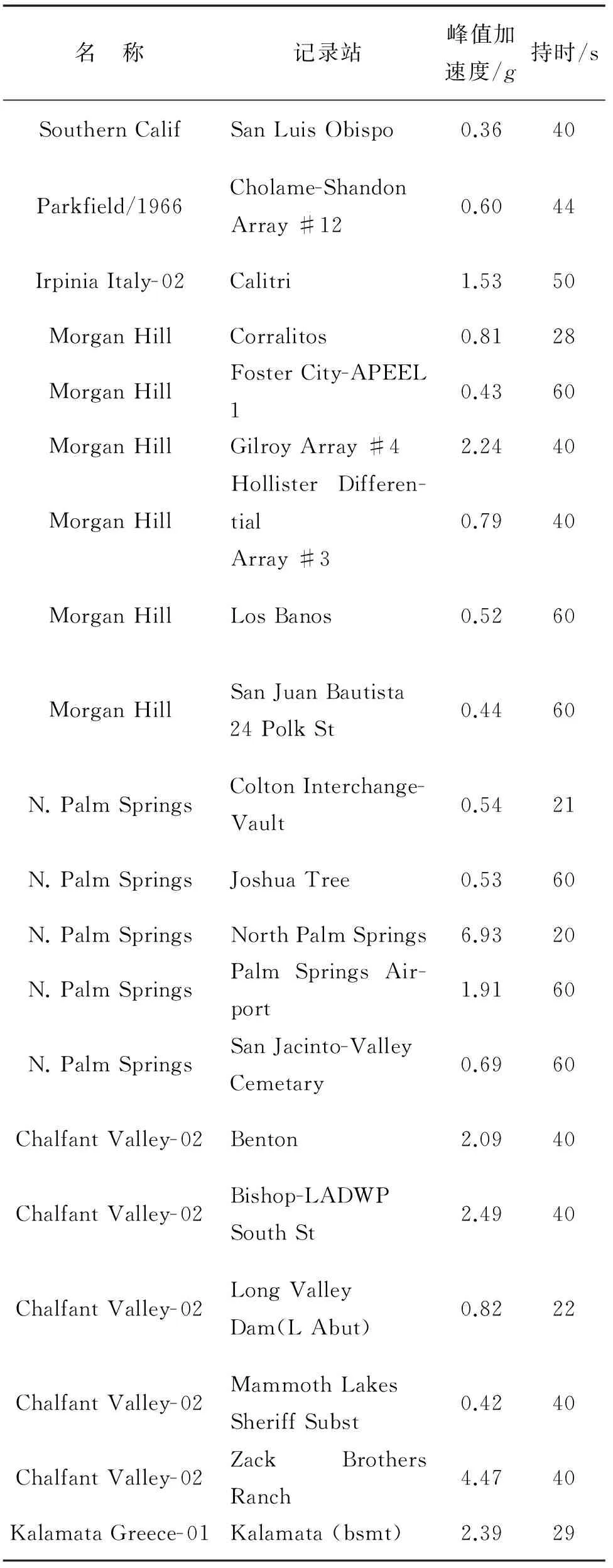
表1　算例Ⅰ所选地震动记录[19]

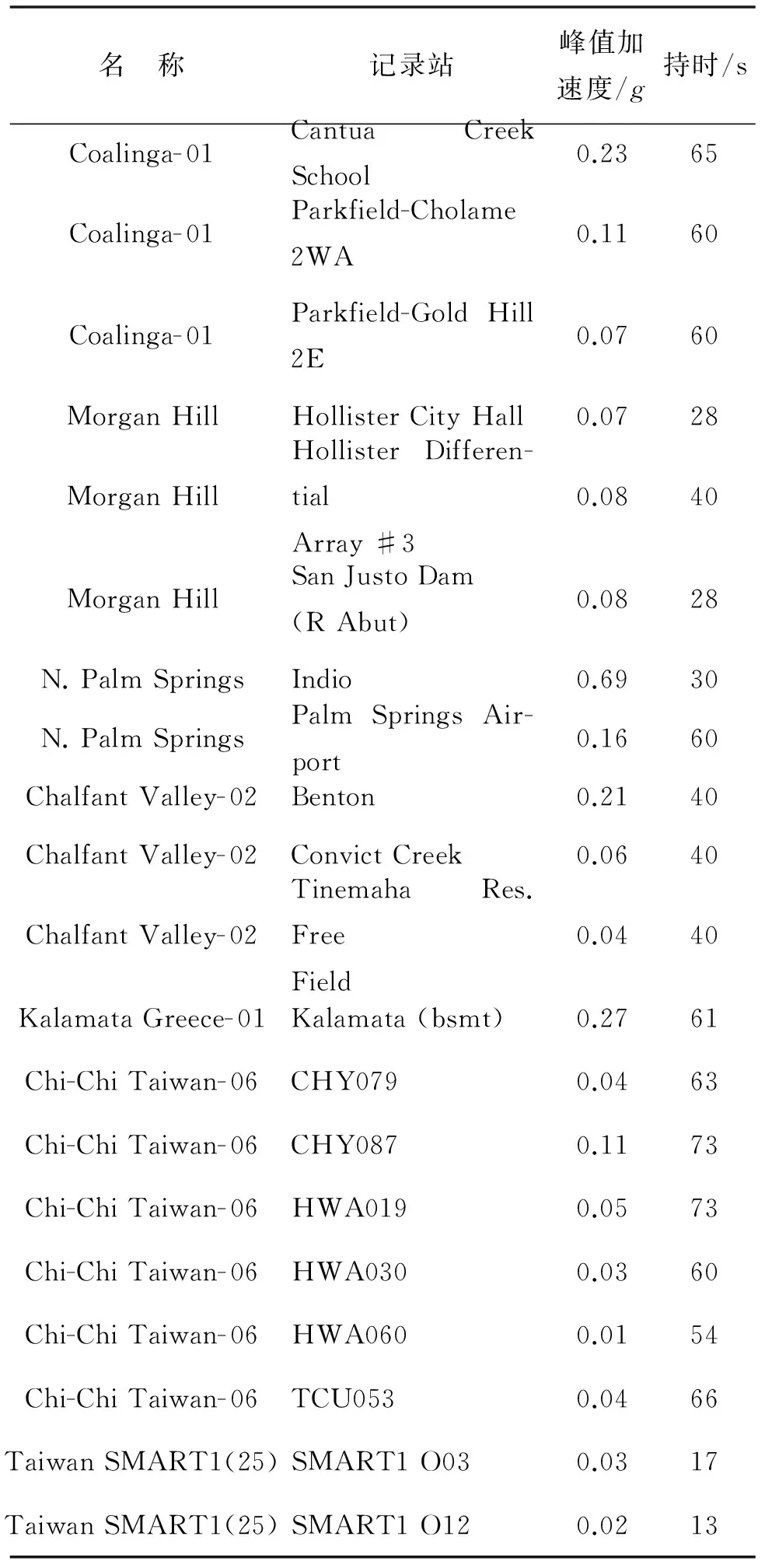
表2　算例Ⅱ所选地震动记录[19]

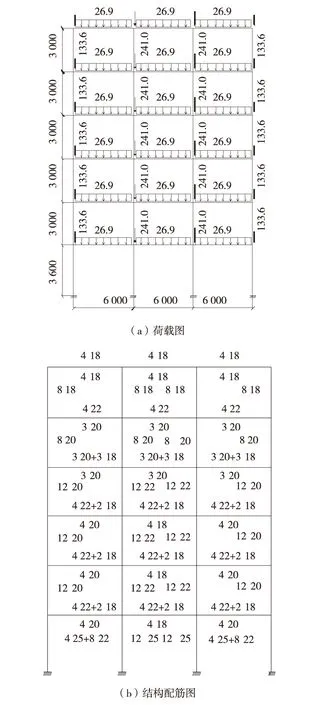
图5　六层结构模型(单位：mm)Fig.5　Six-story structure configuration(unit：mm)

分别对结构进行前3阶模态推覆分析，其中发现第2、第3阶模态不具有软化段，因此只对第1阶模态推覆曲线进行三线性等效. 图6为算例1的1阶模态推覆曲线和分别进行双线性和三线性拟合后的曲线，由图6可见，使用三线性拟合后的屈服力和屈服位移均小于使用双线性拟合后的屈服力和屈服位移，且三线性拟合曲线的最大力也小于双线性拟合曲线的屈服力，因此可以预测三线性拟合方法计算的地震力比相应的双线性拟合方法计算的值要小．图7和图8为模态推覆分析分别采用双线性和三线性拟合方法的计算结果与原多自由度结构非线性动力时程分析计算结果的对比图，比较结果印证了上述预测．由图7可知，三线性拟合方法计算的楼层位移比相应的双线性拟合方法计算的楼层位移更接近于非线性动力时程分析计算结果，三线性拟合方法计算结果最大误差不超过5%，而双线性拟合方法计算结果最大误差接近20%，如图9(a)．三线性拟合方法计算的层间位移角误差除了在第4和第5层稍大于双线性拟合方法的相应值外，其他层均小于双线性拟合方法的相应值，且其最大误差不超过15%，而双线性拟合方法计算值误差接近20%，如图9(b)．

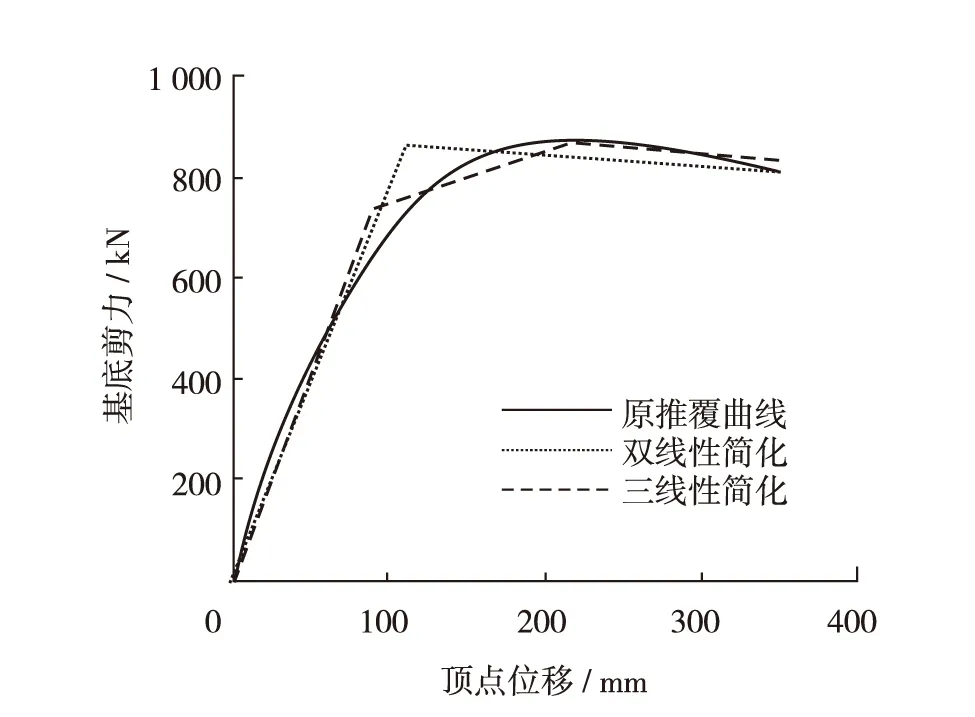
图 6　算例Ⅰ结构一阶模态推覆曲线及双线、三线性拟合曲线Fig.6　Pushover curve, bilinear and trilinear fitting curves of the 1st mode for the first case

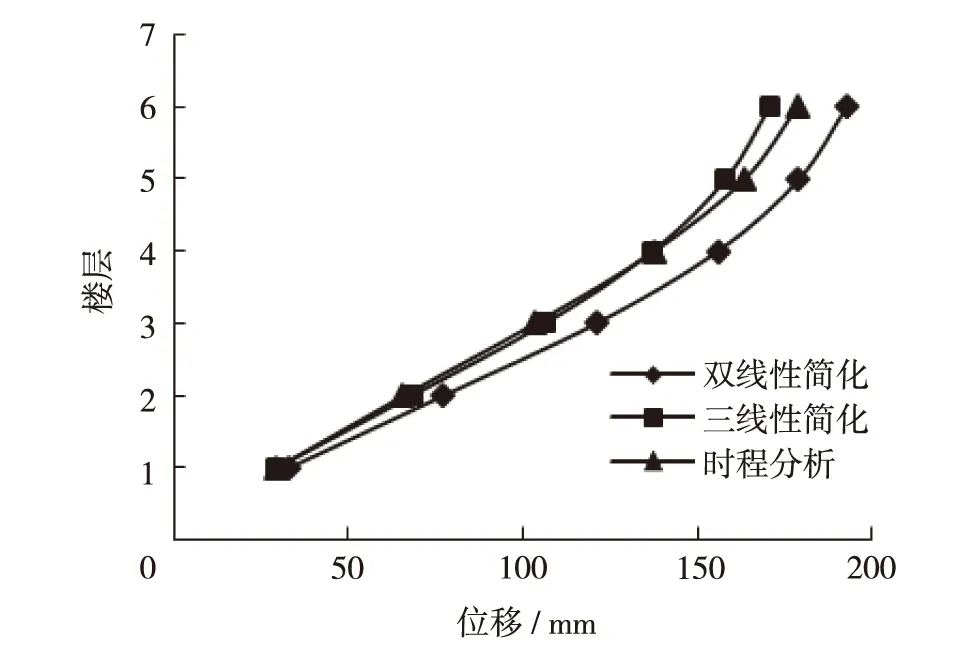
图7　算例Ⅰ楼层位移对比Fig.7　Comparison of floor displacements of the first case

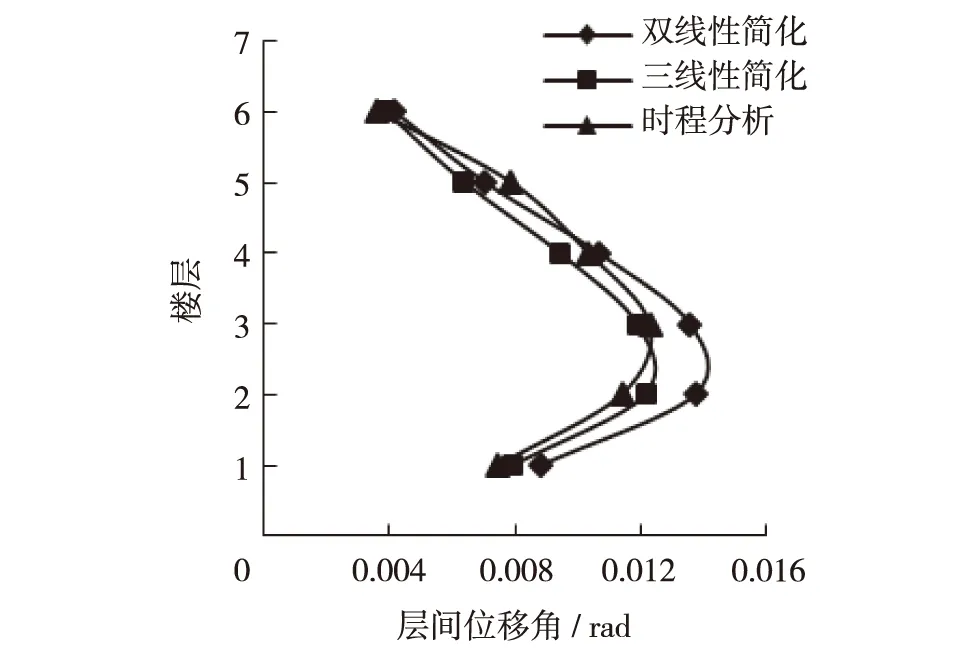
图8　算例Ⅰ层间位移角对比Fig.8　Comparison of story drift ratios of the first case

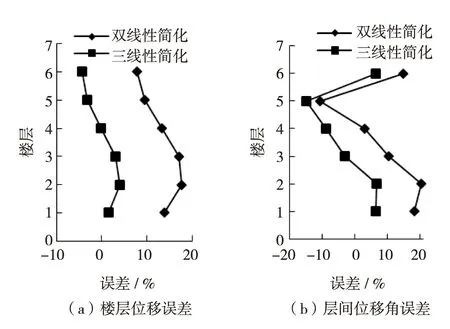
图9　算例Ⅰ误差对比Fig.9　Error comparison for the first case

2.3算例Ⅱ

算例Ⅱ为一个9层结构，设防烈度也为8度0.2g， 柱尺寸600 mm×600 mm，梁尺寸300 mm×550 mm，由于和算例Ⅰ模型类似，此处未给出详细的模型图，仅给出非线性时程分析、双线性和三线性拟合方法的计算结果对比图，建模方法和参数取值类似于算例Ⅰ．此例也仅第1节模态需要进行三线性等效．

图10和图11分别为算例Ⅱ的楼层位移和层间位移角对比.由图10可见，三线性拟合方法计算的楼层位移值比双线性拟合方法计算的楼层位移值更接近于非线性动力时程分析计算结果，双线性拟合方法计算的楼层位移误差可达50%．而三线性拟合方法计算的楼层位移误差最大值不到15%，如图12(a)．由图11可以看出，对于层间位移角的计算值，在第8层和第9层双线性拟合方法稍微比三线性拟合方法的计算值接近于非线性动力时程分析值，而在其他层，三线性拟合方法更接近于非线性动力时程分析结果(注意到层间位移角最大值出现在第4层)，双线性拟合方法的误差最大值可达55%，而三线性拟合方法误差最大值仅为15%左右，如图12(b)．

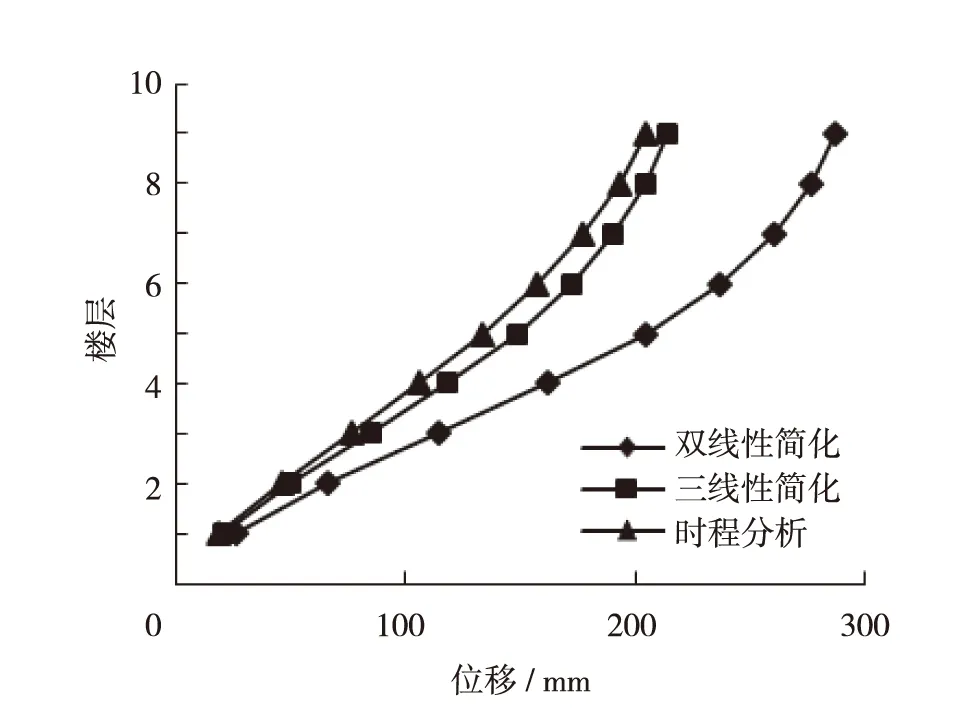
图10　算例Ⅱ楼层位移对比Fig.10　Comparison of floor displacements of the second case

图11　算例Ⅱ层间位移角对比Fig.11　Comparison of story drift ratios of the second case

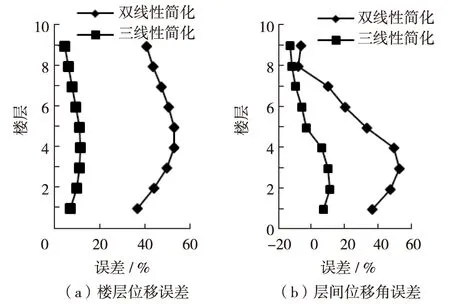
图12　算例Ⅱ误差对比Fig.12　Error comparison for the second case

综合算例Ⅰ和算例Ⅱ的分析可知，相对于传统的双线性拟合方法，带有弹性、硬化和软化片段的三线性拟合方法的曲线更接近于结构实际软化的推覆曲线，能更好的预测结构能力曲线的屈服点和最大值点，更接近于实际情况，因此计算结果也更接近于原结构非线性动力时程分析的结果．

3　结　论

对于软化的静力推覆曲线，本研究提出了三线性分段等能量拟合方法对其推覆曲线进行简化拟合，阐述了三线性拟合方法的具体步骤，并采用两个算例验证该方法的准确性，可知：

1)对于软化的静力推覆曲线，使用三线性拟合方法得到的曲线更接近于结构实际推覆曲线，能更好地预测结构能力曲线的屈服点和最大值点，其地震位移需求结果较双线性拟合方法更接近于非线性动力时程分析结果，精度更高；

2)本研究在简化成等效单自由度体系时，其滞回模型采用的是完全弹塑性模型，不同滞回模型对计算结果影响如何，哪种滞回模型更接近于实际情况，尚需进一步研究．

/

[1] Chopra A K, Chintanapakdee C. Inelastic deformation ratios for design and evaluation of structures: single-degree-of-freedom bilinear systems[J]. Journal of Structural Engineering, 2004, 130(9): 1309-1319.

[2] Michel C, Lestuzzi P, Lacave C. Simplified non-linear seismic displacement demand prediction for low period structures[J]. Bulletin of Earthquake Engineering, 2014, 12(4): 1-19.

[3] Chopra A K, Goel R K. A modal pushover analysis procedure for estimating seismic demands for buildings[J]. Earthquake Engineering & Structural Dynamics, 2002, 31(3): 561-582.

[4] Chopra A K, Goel R K, Chintanapakdee C. Evaluation of a modified MPA procedure assuming higher modes as elastic to estimate seismic demands[J]. Earthquake Spectra, 2004, 20(3): 757-778.

[5] Chopra A K, Goel R K. A modal pushover analysis procedure to estimate seismic demands for unsymmetric-plan buildings[J]. Earthquake Engineering & Structural Dynamics, 2004, 33(8): 903-927.

[6] Gupta B, Kunnath S K. Adaptive spectra-based pushover procedure for seismic evaluation of structures[J]. Earthquake Spectra, 2000, 16(2): 367-392.

[7] Antoniou S, Pinho R. Advantages and limitations of adaptive and non-adaptive force-based pushover procedures[J]. Journal of Earthquake Engineering, 2004, 8(4): 497-522.

[8] Antoniou S, Pinho R. Development and verification of a displacement-based adaptive pushover procedure[J]. Journal of Earthquake Engineering, 2004, 8(5): 643-661.

[9] Kalkan E, Kunnath S. Adaptive modal combination procedure for nonlinear static analysis of building structures[J]. Journal of Structural Engineering, 2006, 132(11): 1721-1731.

[10] 毛建猛, 谢礼立, 翟长海. 模态pushover分析方法的研究和改进[J]. 地震工程与工程振动, 2006, 26(6): 50-55.

Mao Jianmeng, Xie Lili, Zhai Changhai. Studies on and improvements in modal pushover analysis[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(6): 50-55.(in Chinese)

[11] Poursha M, Khoshnoudian F, Moghadam A S. A consecutive modal pushover procedure for estimating the seismic demands of tall buildings[J]. Engineering Structures, 2009, 31(2): 591-599.

[12] Poursha M, Khoshnoudian F, Moghadam A S. A consecutive modal pushover procedure for nonlinear static analysis of one-way asymmetric plan tall building structures[J]. Engineering Structures, 2011, 33(9): 2417-2434.

[13] Poursha M, Khoshnoudian F, Moghadam A S. The extended consecutive modal pushover procedure for estimating the seismic demands of two-way unsymmetric-plan tall buildings under influence of two horizontal components of ground motions[J]. Soil Dynamics & Earthquake Engineering, 2014, 63(1): 162-173.

[14] 杨红, 臧登科, 闻奇光, 等. Modal Pushover的改进方法及误差评估[J]. 重庆大学学报自然科学版, 2009, 32(1): 37-43.

Yang Hong, Zang Dengke, Wen Qiguang, et al. An improved method for and error evaluation of modal pushover analysis[J]. Journal of Chongqing University Natural Science Edition, 2009, 32(1): 37-43.(in Chinese)

[15] 闻奇光. 模态Pushover的影响因素评估及改进方法研究[D]. 重庆:重庆大学, 2007.

Wen Qiguang. An evaluation on the effect factor and investigation on the improving method of the model pushover analysis[D]. Chongqing:Chongqing University, 2007.(in Chinese)

[16] Han S W, Moon K H, Chopra A K. Application of MPA to estimate probability of collapse of structures[J]. Earthquake Engineering & Structural Dynamics, 2010, 39(11): 1259-1278.

[17] 施炜, 陆新征, 叶列平, 等. 建筑结构倒塌分析的单自由度模型[J]. 工程力学, 2012, 29(10): 5-12.

Shi Wei, Lu Xinzheng, Ye Lieping, et al. Single-degree of freedom hysteretic model for collapse analysis of building structures[J]. Engineering Mechanics, 2012, 29(10): 5-12.(in Chinese)

[18] 毛建猛. Pushover分析方法的改进研究[D]. 哈尔滨：中国地震局工程力学研究所, 2008: 19-20.

Mao Jianmeng. Improvements on pushover analysis procedure[D]. Harbin: Institute of Engineering Mechanics, China Earthquake Administration, 2008: 19-20.(in Chinese)

[19] Pacific Earthquake Engineering Research Center. PEER Ground Motion Database[DB/OL]. Berkeley: PEER[2016-01-21]http://ngawest2.berkeley.edu/site.

[20] 杨溥，李英民，赖明. 结构时程分析法输入地震波的选择控制指标[J]. 土木工程学报, 2000, 33(6): 33-37.

Yang Pu, Li Yingmin, Lai Ming. A new method for selecting inputting waves for time-history analysis[J].China Civil Engineering Journal, 2000, 33(6): 33-37.(in Chinese)

[21] GB50010—2010混凝土结构设计规范[S].

GB50010—2010 Code for design of concrete structures[S].(in Chinese)

【中文责编：坪梓；英文责编：之聿】

2016-03-28；Accepted：2016-06-01

Piecewise linear fitting of softening static pushover curves

Xiang Chang，Peng Jun，and Su Liang†

College of Civil Engineering and Architecture, Zhejiang University, Hangzhou 310058, Zhejiang Province, P.R.China

Because the traditional bilinear fitting method is difficult to fit softening static pushover curves, we propose the trilinear piecewise linear fitting method to fit such curves based on equal energy rules. The processes are provided step by step. Taking two reinforced concrete frame structures as examples, we fit softening static pushover curves of the cases with both bilinear and trilinear fitting methods, and compare the results of the two methods with the results computed by nonlinear dynamic time history method respectively. Research indicates that the proposed trilinear fitting method is more accurate than the traditional bilinear method for structures whose pushover curves have descending branch.

structural engineering; pushover analysis; pushover curves; bilinear fitting method; trilinear fitting method; nonlinear dynamic time history analysis

Xiang Chang，Peng Jun，Su Liang．Piecewise linear fitting of softening static pushover curves[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(5): 476-483.(in Chinese)

TU 973.31

Adoi：10.3724/SP.J.1249.2016.05476

国家重点技术支撑计划资助项目(2012BAJ07B03)

向畅(1992—)，男，浙江大学硕士研究生.研究方向：结构抗震．E-mail:xiangc@zju.edu.cn

Foundation：National Key Technology Support Program (2012BAJ07B03)

† Corresponding author：Associate professor Su Liang．E-mail: suliang@zju.edu.cn

引文：向畅，彭军，苏亮．软化静力推覆曲线的分段线性拟合[J]. 深圳大学学报理工版，2016，33(5)：476-483.