基于增量非负矩阵分解的自适应背景模型
2016-10-21董怀琴潘彬彬陈文胜
董怀琴,潘彬彬,陈文胜,徐 晨
1) 深圳大学数学与统计学院,广东深圳 518060;2) 深圳大学智能计算科学研究所,广东深圳 518060
【电子与信息科学 / Electronics and Information Science】

基于增量非负矩阵分解的自适应背景模型
董怀琴1,潘彬彬1,陈文胜1,徐晨2
1) 深圳大学数学与统计学院,广东深圳 518060;2) 深圳大学智能计算科学研究所,广东深圳 518060
提出一种基于增量非负矩阵分解的自适应背景模型,以处理动态背景变化.当有新的数据流到达时,利用增量非负矩阵分解有效地更新背景模型.实验结果表明,与非负矩阵分解相比,增量非负矩阵分解不仅运算时间更少,而且能够提取出更好的前景.
应用数学;非负矩阵分解;背景建模;增量学习;特征提取;满秩分解;前景提取
背景模型是一种检测运动物体的常用方法.通过将当前帧与背景相减,可以得到前景,以此进行物体分割、检测和追踪[1-5].背景是包含静止物体的场景,如房子、树、墙壁及家具等.前景则是非静止的物体,包括运动的汽车、行走或跑动的人.由于背景随着物体的运动而动态变化,如原本静止的汽车离开了,或者是运动的人静止了,因此,需要自适应地更新背景模型.
当从一系列的帧之中提取背景时,由于这些帧的背景是一致的,可以认为背景是这些帧的主要成分,而前景为稀疏成分.因此,可以采用子空间的方法,如主成分分析(principal component analysis, PCA)[6]和非负矩阵分解(non-negative matrix factorization, NMF)[7],对一系列帧提取其主要成分.这些主要成分就是所需要的背景,通过将一帧在这些成分张成的子空间上进行投影,再重构回来,就可以得到这帧的背景表达.于是,前景可以通过此帧与背景的相减得到.
然而当背景变化时,由于PCA和NMF只能处理静态的数据,因此它们需要将所有帧重新进行分解,这样会非常耗时.监控视频数量的不断增长迫切需要高效率的自适应背景建模算法[8-10].Bucak等[11]提出增量子空间学习的方法,采用重构误差作为目标函数,在求解过程中利用之前得到的子空间信息,自适应地更新子空间,从而加快分解速度,有效对自适应背景建模.然而,Bucak的方法每次只能增量地学习1帧.若需要增量学习多帧,则算法需要执行多次,这样就降低了算法的效率.Cao 等[12]提出利用在线非负矩阵分解(online non-negative matrix factorization, ONMF)来检测和追踪潜在因子.因子是随着数据流而动态变化的,ONMF能较好追踪到变化的因子,成功运用到了主题检测.
本研究利用ONMF算法进行动态的背景建模,称此方法为增量非负矩阵分解(incremental non-negative matrix factorization, INMF).与文献[11]的方法相比,INMF方法能同时处理多帧,因此具有更好的计算效率.实验结果表明,INMF不仅在计算时间上,而且在前景检测上,都要优于NMF.
1 非负矩阵分解
NMF的思想是将一个非负矩阵V近似分解为2个非负矩阵的乘积,即
Vm×n≈Wm×rHr×n
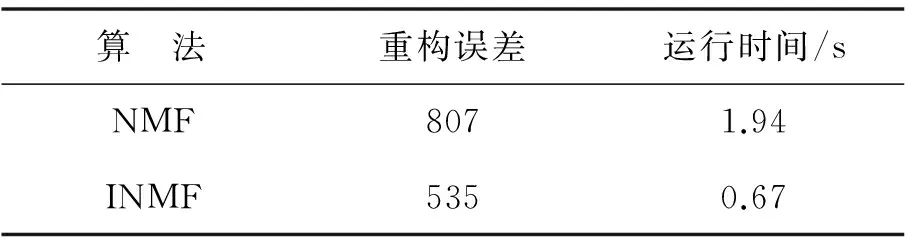
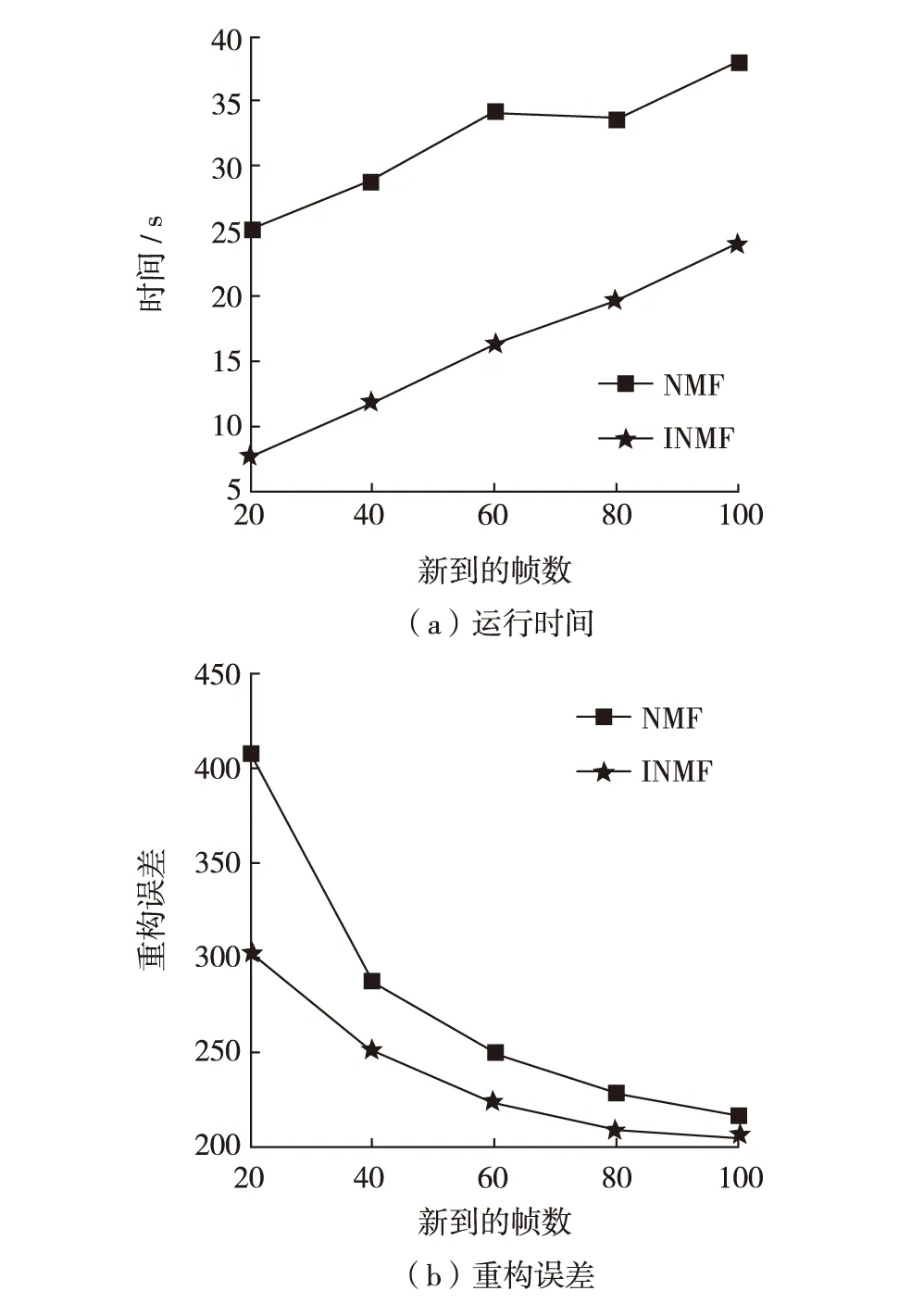
其中, Wm×r和Hr×n都是非负矩阵; r为基向量的个数,一般选择r满足(m+n)r V和WH之间的误差定义为[6] (1) NMF要解决如下最优化问题 以上最优化问题可用如下迭代公式求解[13] 文献[13]证明了目标函数(1)在上述迭代算法下是非递增的. 利用传统NMF对数据流进行处理是不现实的.假设在t时刻得到数据V, 并采用NMF算法得到如下分解: V=WH 在t+1时刻,有新的数据U到达.因此,数据矩阵变为 引理1[12]若V=WH和V=W′H′是V的两个满秩分解,那么存在可逆矩阵P, 满足W=W′P和H=P-1H′. 考虑分解 (2) (3) 其中, P为可逆矩阵.于是,分解问题(2)转变为 (4) 为了求解问题(4),考虑如下分解 可得 更新规则为 3.1实验数据库及实验方法 在背景模型实验中,我们使用PET2001的 “dataset1_camera1” 的视频数据库[14].这段视频时长2 min 2 s,共3 064帧,每帧大小为576×768.为提高计算效率,每帧采样都降到144×192,然后排成144×192=27 648维的列向量. 其中, W+为广义逆.重构误差使用Frobenius范数,即 3.2动态背景建模结果 在第1部分实验中,第1次选取181~200帧及281~290帧,共30帧用NMF做训练,然后选取第250帧做测试.随后新的视频流2 781~2 790帧到达,这时背景已发生变化,此时分别用NMF和INMF做训练,然后用第2 800帧做测试,比较运算时间与重构误差.第1次训练的第181帧和第2次训练的第2 781帧见图1.值得注意的是,第2次训练时,背景已发生变化,图1(a)中标注车辆在图1(b)中已消失. 第1次训练的两个背景基见图2(a)和图2(b).也许是因为训练帧里都包含前景的人,所以背景基不能很好地将人剔除出去.将测试帧投影到子空间的图像和提取的前景见图2(c)和图2(d).可见,NMF能够提取出需要的前景图像. 第2次训练时,有新的帧到达,NMF和INMF分别使用第2 781~2 790帧训练,提取的背景基分别见图3(a)、图3(b)和图4(a)、图4(b).由于背景变化了,而INMF进行加权方案,新到的帧对背景基的贡献更大,所以INMF提取的背景基效果会更好一些. 图2 第1次训练的结果Fig.2 The results of the first training 图3 NMF的结果Fig.3 The results of NMF 图4 INMF的结果Fig.4 The results of INMF 将测试帧投影到NMF训练出的子空间的图像和提取的前景见图3(c)和图3(d);同样,投影到INMF训练出的子空间图像和提取的前景见图4(c)和图4(d).可见,INMF能很好地将前景提取出来,而NMF则留有残影.NMF和INMF的重构误差与运行时间见表1.可见,INMF具备更小的重构误差及更快的运算速度. 表1 重构误差与运行时间比较 3.3运算时间与重构误差比较 在第2部分实验中,首先选取181~280帧总共100帧作为第1次训练,随后新的视频流到达,分别采用NMF和INMF对新到达的数据做第2次训练.新的视频流分别选取2 781~2 800、2 781~2 820、2 781~2 840、2 781~2 860及2 781~2 880帧5种情况,然后用第2 900帧做测试,比较运算时间与重构误差.此时p的取值分别为20、40、60、80和100. NMF和INMF算法的运行时间和重构误差如图5.可见,INMF用时比NMF少,且两个算法的运算时间随着帧数的增加呈线性增长趋势.同时,INMF具备更小的重构误差.当帧数很少时,INMF的重构误差显著低于NMF,表明INMF只需少量的新数据流即可取得不错的结果.在帧数增加时,NMF的重构误差渐趋于INMF.这说明新数据流足够多时,两个算法的结果比较接近. 图5 运行时间与重构误差Fig.5 Running time and reconstruction error 本研究使用INMF进行自适应背景建模.与静态NMF相比,INMF能很好地根据视频流进行背景模型更新.通过实验比较,INMF能够提取出更好的前景,并具有更短的运算时间.下一步工作可考虑使用二维或张量非负矩阵方法进行背景建模,这样可以更有效地提高运算效率,满足视频监控的实时要求. / [1] Jeeva S,Sivabalakrishnan M.Survey on background modeling and foreground detection for real time video surveillance[J].Procedia Computer Science,2015,50:566-571. [2] Bouwmans T.Traditional and recent approaches in background modeling for foreground detection:an overview[J].Computer Science Review,2014,11(12):31-66. [3] Cristani M,Farenzena M,Bloisi D,et al.Background subtraction for automated multisensory surveillance:a comprehensive review[J].Eurasip Journal on Advances in Signal Processing,2010,43(24):25-31. [4] Bouwmans T, El-Baf F,Vachon B.Statistical background modeling for foreground detection: a survey[J].Handbook of Pattern Recognition and Computer Vision,2010,4(2):181-199. [5] Radke R,Andra S,Al-Kofahi O,et al.Image change detection algorithms: a systematic survey[J].IEEE Transactions on Image Processing,2005,14(3):294-307. [6] Jolliffe I T.Principal component analysis[M].New York, USA: Springer-Verlag,1986. [7] Lee D,Seung H.Learning the parts of objects by non-negative matrix factorization[J].Nature,1999,401(6755):788-791. [8] Zhang Xiaoguo, Huang Tiejun,Tian Yonghong,et al.Background-modeling-based adaptive prediction for surveillance video coding[J].IEEE Transactions on Image Processing, 2014,23(2):769-784. [9] Popa S,Crookes D, Miller P.Hardware acceleration of background modeling in the compressed domain[J].IEEE Transactions on Information Forensics and Security,2013,8(10):1562-1574. [10] Rodriguez P, Wohlberg B.A Matlab implementation of a fast incremental principal component pursuit algorithm for video background modeling[C]// IEEE International Conference on Image Processing. Paris: IEEE, 2014:3414-3416. [11] Bucak S,Gunsel B.Incremental subspace learning via non-negative matrix factorization[J].Pattern Recognition,2009,42(5):788-797. [12] Cao Bin,Shen Dou,Sun Jiantao,et al. Detect and track latent factors with online non-negative matrix factorization[C]// Proceedings of the 20th international joint conference on Artifical intelligence. San Francisco, USA: ACM, 2007:2689-2694. [13] Lee D,Seung H.Algorithms for non-negative matrix factorization[J].Nips,2010, 32(6): 556-562. [14] PETS Video Database (http://ftp.pets.rdg.ac.uk/). 【中文责编:方圆;英文责编:木南】 2015-12-31;Revised:2016-07-01;Accepted:2016-07-07 Adaptive background modeling via incremental non-negative matrix factorization Dong Huaiqin1, Pan Binbin1†,Chen Wensheng1,and Xu Chen2 1) College of Mathematics and Statistics, Shenzhen University, Shenzhen 518060, Guangdong Province, P. R. China 2) Institute of Intelligent Computing Science, Shenzhen University, Shenzhen 518060, Guangdong Province, P. R. China A method for adaptive background modeling based on the incremental non-negative matrix factorization (INMF) is proposed. INMF is used to update new background models effectively when new data streams arrive. The experimental results show that, compared with non-negative matrix factorization (NMF), INMF not only takes less running time but also can be used to extract better foregrounds. applied mathematics; non-negative matrix factorization; background modeling; incremental learning; feature extraction; full rank factorization; foreground extraction Dong Huaiqin, Pan Binbin,Chen Wensheng, et al. Adaptive background modeling via incremental non-negative matrix factorization[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(5): 511-516.(in Chinese) TP 391 Adoi:10.3724/SP.J.1249.2016.05511 国家自然科学基金资助项目(11526145, 61272252, 11501377) 董怀琴 (1992—),女,深圳大学硕士研究生.研究方向:模式识别与机器学习. E-mail:1018498868@qq.com Foundation:National Natural Science Foundation of China (11526145, 61272252, 11501377) † Corresponding author:Lecturer Pan Binbin. E-mail: pbb@szu.edu.cn 引文:董怀琴,潘彬彬,陈文胜,等. 基于增量非负矩阵分解的自适应背景模型[J]. 深圳大学学报理工版,2016,33(5):511-516.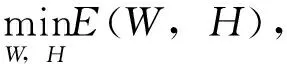
2 增量非负矩阵分解
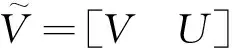
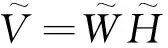
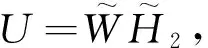
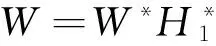
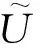
3 背景模型实验
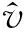
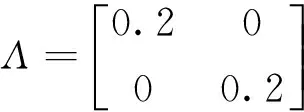



结 语
