平衡大气边界层自保持及TTU风压数值模拟

杨　磊，李　磊，杨向龙

深圳大学土木工程学院，广东深圳 518060



平衡大气边界层自保持及TTU风压数值模拟

杨磊，李磊，杨向龙

深圳大学土木工程学院，广东深圳 518060

构造合理且满足水平均匀性的大气边界层是计算风工程的一个重要难题．基于雷诺平均方法，采用标准k-ε湍流模型，结合Richards & Hoxey入口条件，对数值风洞的顶面边界条件施加剪切应力修正，进行二维空流场的平衡大气边界层模拟，给出了一类能够较好满足大气边界层自保持要求的流场边界条件．并将此类边界条件同时运用到标准k-ε湍流模型和SST (shear stress transport)k-ω湍流模型中，针对美国德克萨斯技术大学模型场地试验进行三维流场全尺寸数值模拟，验证了所提边界条件对上述两类双方程湍流模型在低矮建筑钝体绕流的适用性．

计算风工程；平衡大气边界层；水平均匀性；标准k-ε湍流模型；顶部边界条件；德克萨斯技术大学模型

计算风工程(computational wind engineering, CWE)是利用计算流体动力学(computational fluid dynamics, CFD)方法研究不同类型建筑结构风荷载和风环境的学科．其中，准确模拟大气边界层内的湍流流动是利用数值方法研究结构风特性的重要前提．计算风工程应首先满足大气边界层(atmosphere boundary layer, ABL)的水平均匀性(horizontal homogeneity)要求．水平均匀性是指在没有障碍物的简单边界层流动下，数值风洞内风剖面的物理参数与测量地点无关，即计算域入口处定义的流动物理量(速度、湍动能和湍流耗散率等)，从入口到出口保持一致．满足水平均匀性要求的边界层称为平衡大气边界层．大气边界层的水平均匀性对CFD模拟结果的准确性有显著影响．

在数值风洞内平衡大气边界层，影响自保持水平均匀性的主要因素包括边界条件、湍流模型、壁面处理和网格划分等方面．Richards等[1-3]提出入流边界、湍流模型和地面粗糙度的综合作用会产生一个内边界层(internal boundary layer, IBL)，使得风剖面在到达建筑物之前发生较大的改变；同时研究了来流边界条件的合理给定问题，给出了一组基于标准k-ε湍流模型的入口边界条件(Richards & Hoxey (RH)入口条件)．Juretic＇等[4]通过研究雷诺应力结合壁面函数的修正，给出了适用于标准k-ω湍流模型的来流边界条件．曾锴[5]基于shear stress transport (SST) k-ω湍流模型，考察了不同入口边界条件的设置对钝体绕流计算结构的影响，提出了入口湍流风剖面自保持的表达方法．杨伟等[6-8]从模型方程本身出发，基于风洞实验数据，推导出一类近似满足k-ε模型自保持边界要求的入口湍动能表达式，并定义了模型常数．顾明等[9]研究了壁面Y+值对平衡大气边界层数值模拟结果的影响，结果表明相比于近壁面函数，通过近壁面网格来预测湍流的产生能提高模拟的准确性．孙玉航等[10]针对平衡大气边界层，基于标准k-ε湍流模型，通过推导耗散率表达式，并在输运方程中添加源项的方法，得到了一类较为适用的边界条件．

对于计算域顶部，常用的边界条件有对称边界条件[11]、速度边界条件[12]、压力出口边界条件[13]和剪切应力边界条件[1,11]．顶部边界条件对计算结果会产生较大影响．从理论上来说，剪切应力边界条件更符合物理实际，并且在计算域顶部施加剪切应力边界条件确实可以得到很好的结果．然而，正如Hargreaves等[11]指出的，这种边界条件在通用的CFD模拟软件(如Fluent和CFX等)中难以实现，因此，被很多研究者忽略．Richards等[1]提出了通过在靠近顶部边界的一层网格中增加动量和湍流耗散率源项的方法来施加剪切应力的思想，但他们并没有给出相应的源项公式．目前已有的数值模拟研究中，尚未构造出全部主要特征量均能够很好满足水平均匀性的数值风洞．

本研究基于标准k-ε湍流模型，采用RH入口条件，提出并验证了一种便于实现并能较好满足大气边界层自保持要求的顶部边界条件．采用此类边界条件对美国德克萨斯技术大学(Texas Tech University, TTU)建筑周围风场进行了数值模拟，将模拟结果与实测数据进行分析对比，验证了该方法的可行性．

1　边界条件和模型参数

基于ANSYS—Fluent 15.0平台，利用标准k-ε湍流模型，研究顶部边界条件对平衡大气边界层自保持特性的影响．针对无建筑物扰动的空流场特征，采用二维数值模拟以突出重点和提高效率．计算区域尺寸为1 000 m×300 m，计算域内未放置任何障碍物．采用结构网格对计算域进行离散化处理，近地面沿高度方向最小网格大小为0.01 m，竖向增长因子为1.05，网格单元总数约为40 000个，如图1．

图1　计算网格Fig.1　Calculation mesh

计算域入口统一采用velocity-inlet边界条件，速度和湍动能以及湍流耗散率的数值利用RH入口条件确定．

来流风速剖面u(z)采用对数率表达为

(1)

湍动能k为

(2)

湍流耗散率ε为

(3)

其中，u*为摩擦速度，根据参考高度处的参考风速确定；κ为Von Karman常数，取κ= 0.41； z为离地面的高度； z0为粗糙度长度，取z0=0.01m；Cμ为k-ε湍流模型常数，取0.09．

计算域地面采用固壁边界条件，引入粗糙壁面修正．粗糙度常数Cs、 粗糙度高度Ks以及粗糙度长度z0满足式(4)，

CsKs≈9.793z0

(4)

其中， Cs=0.5， Ks=20， z0=0.2．

出流面采用完全发展出流边界条件为

(5)

其中， x表示顺流方向； u、 v和w分别为3个方向的速度分量．

对于计算域顶部边界条件，本研究提出了一种容易在通用CFD模拟软件中实现的施加剪切应力的方法．对紧靠顶部边界的两层网格，直接施加满足式(1)至式(3)的速度、湍动能和湍流耗散率的条件．通过给定顶部边界附近的物理梯度的方法，达到施加剪切应力的目的．

为比较分析顶部边界条件对大气边界层自保持特性的影响，采用4种不同顶部边界条件计算流域顶部，分别为对称边界条件、指定速度和湍动能的速度入口边界条件、静压边界条件以及在计算域顶部施加剪切应力边界条件．

流动视为定常不可压缩流，采用速度-压力耦合方式(semi-implict method for pressure-linked equations consistent，SIMPLEC)，对流项采用二阶迎风格式进行离散化．当所有相关变量的迭代残差达到平稳且监测的某些典型物理量不再显著变化时，判定计算收敛．

2　数值结果

为比较各工况下平衡大气边界层效果，选取入流面、入流面下游300和600 m及出流面4个不同观测位置相应的速度、湍动能和湍流耗散率等关键物理量进行比较．

图2为4种不同计算工况下，4个不同观测位置平均速度随高度变化曲线．

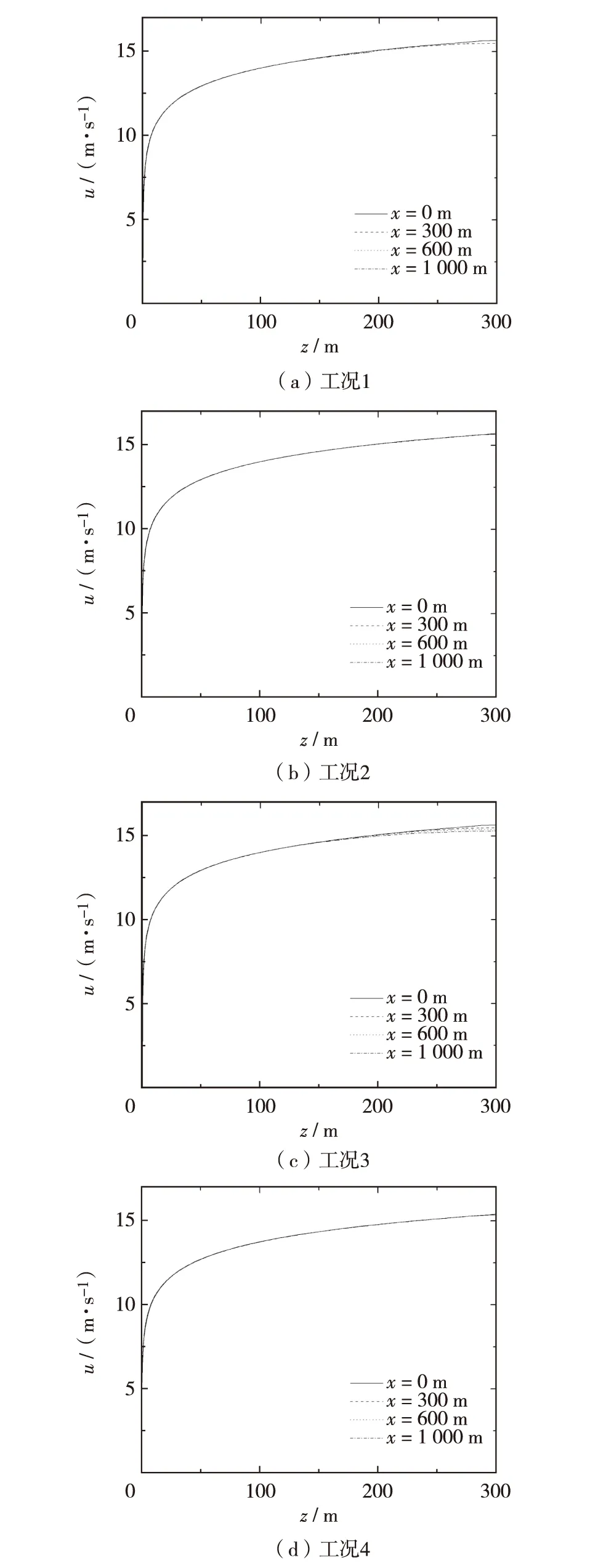
图2　不同工况和不同截面的速度曲线Fig.2　Plots of stream-wise velocity under different conditions with different sections

从图2可见，工况1和工况3的速度曲线在顶部出现了一定的分离，相比工况1的轻微分离，工况3的分离现象更加明显，表明在RH入口条件下，顶部采用压力出口边界条件对速度剖面的水平均匀性有着不利的影响．而工况2和工况4的条件下，各观测位置的速度曲线都能很好的吻合，表现出很好的水平自保持效果．

图3为4种不同计算工况下，4个不同观测位置湍动能随高度变化曲线．

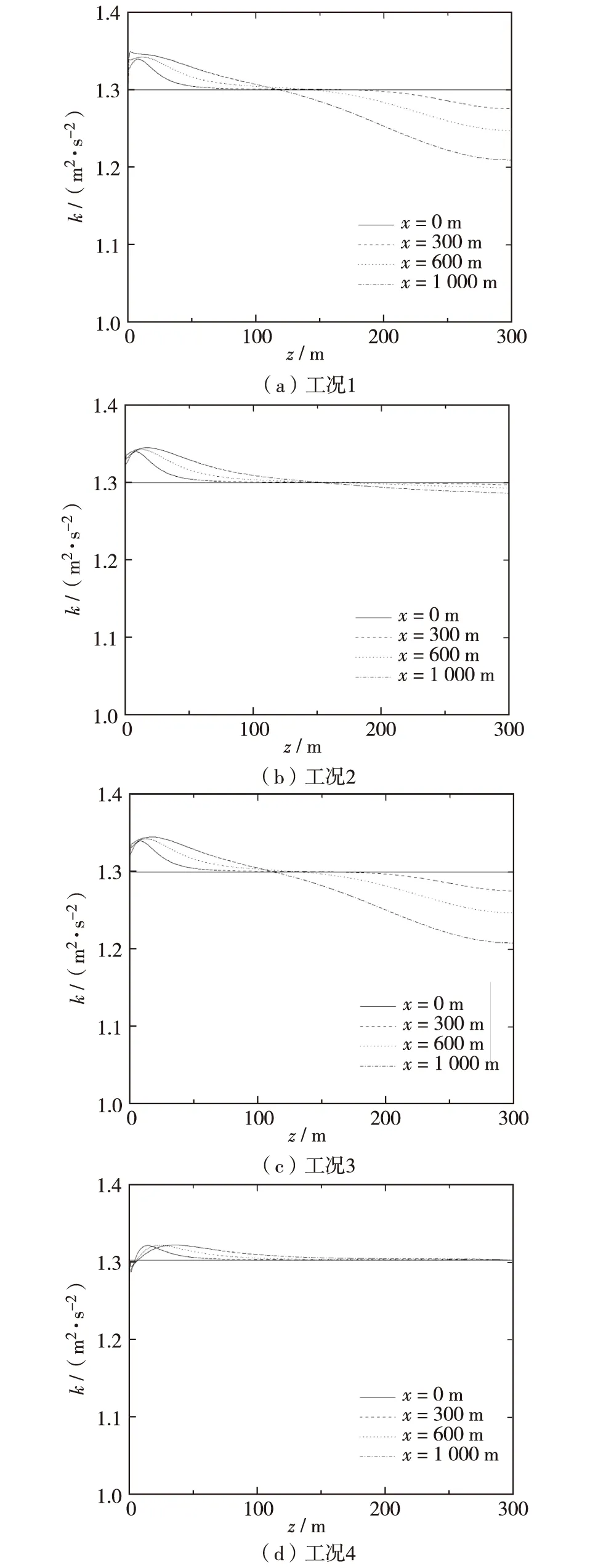
图3　不同工况和不同截面的湍动能曲线Fig.3　Plots of turbulent kinetic energy under different conditions with different sections

由图3可见，工况1至工况3的下游截面湍动能在壁面附近均大于入口处，这种现象在很大程度上是由于数值离散格式所引起的．随着高度的增加，湍动能逐渐减小，顶部位置的湍动能均小于入口处．特别是工况1和工况3，顶部位置的湍动能出现了明显的衰减，这表明顶部设置为对称边界条件和压力出口边界条件，对湍动能剖面的水平均匀性有不利影响，

图3(d)所示工况4中，边界层湍动能剖面在大部分区域保持良好，特别是在顶部，基本与入口处完全吻合，而在近地面小范围区域存在一定的误差． 这种误差可能与壁面粗糙度的设置有关． 入口边界条件所设定的来流中包含的湍流在一定程度上反映出地面粗糙性质，而该性质与计算域地面的固壁边界条件所包含的粗糙性质存在一定的差异，因此，流场在向下游运动的过程中会反映出该差异性．

相比工况1至工况3，工况4在顶部施加剪切应力边界条件后，不但能有效减小计算域顶部的湍动能差异，且能有效降低近地面小范围区域内的湍动能误差．

综上分析表明，入口采用RH入口条件，顶部施加剪切应力边界条件，能够获得较好的平衡大气边界层，实现速度、湍动能和湍流耗散率的自保持性．

3　TTU模型数值模拟

TTU实际尺寸场地试验由美国德克萨斯理工大学的风工程研究现场实验室于1991年完成[14-15]．该实验室建造了一个永久的全尺寸金属建筑用以进行风压的测量．该试验建筑原始尺寸为13.7 m×9.2 m×3.9 m，建筑周围地势开阔平坦，建筑物表面光滑．作为具有代表性的现场实测数据，该试验已成为国际公认的权威的评估数值模拟方法的基准试验，如图4．其中，1#～11#为测试点．

图4　TTU建筑模型尺寸及测点示意图[14]Fig.4　Dimension of TTU building and positions of measure points[14]

文献[16-17]研究结果表明，SST k-ω湍流模型由于能够有效计算湍流切应力在逆压梯度边界层的输运，更适用于钝体分离流模拟．因此，本研究分别采用标准k-ε湍流模型和SST k-ω湍流模型，边界条件采用第2节工况4的设定，针对TTU试验的90°风攻角进行了三维全尺寸数值模拟，并将数值模拟结果与试验结果进行对比．

计算域大小为200 m×100 m×50 m．建筑物放置在入口下游80 m处．设建筑物的长、宽、高分别为L、 B和H， 模型距上游为9L， 距下游为13L， 计算域宽度为7.5B， 在竖直方向上为12.5H， 模型阻塞率为1.1%．计算域采用六面体网格进行划分，网格总数约150万个．

图5为两种湍流模型的数值模拟结果与TTU模型场地实测数据的对比．可见，在90°风攻角的典型计算工况下，采用标准k-ε和SST k-ω两种湍流模型得到的计算结果相差不大，与试验数据总体吻合，均落在TTU建筑现场实测数据的包络线范围内．在模型的迎风面，标准k-ε湍流模型略低于试验结果的平均值，而SST k-ω湍流模型略高，最大偏差为7.4%．

图5　各测点平均风压系数Fig.5　Mean Pressure coefficients of measured points

对于4#测点之后的钝体绕流分离区，两种湍流模型得到的数值模拟结果均略低于TTU试验结果的平均值．最大偏差出现在4#测点，即建筑物迎风面与顶面相交的尖角分离处，此测点处标准k-ε和SST k-ω两种湍流模型的计算结果基本位于试验结果的下限，与试验平均值的误差分别为9.3%和7.9%．在数值模拟通常较为困难的背风面，计算结果整体与试验数据吻合良好．

结　语

基于ANSYS—Fluent 15.0中的标准k-ε湍流模型，利用RH入口条件，通过本研究方法对顶面施加剪切应力边界条件，能够获得较好的平衡大气边界层，实现整个流域内速度、湍动能和湍流耗散率的自保持特性．

在平衡大气边界层的条件下，采用标准k-ε湍流模型和SST k-ω湍流模型均能够较好地对TTU模型场地试验进行数值模拟，分辨钝体流动特征．

/

[1] Richards P J, Norris S E. Appropriate boundary conditions for computational wind engineering models using the k-ε turbulence model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1993, s46/s47(93): 145-153.

[2] Richards P J, Younis B A. Comments on ‘Prediction of wind-generated pressure distribution around buildings’ by Mathews E H[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1990, 34(1): 107-110.

[3] Richards P J, Quinn A D, Parker S. A 6 m cube in an atmospheric boundary layer flow. Part 2, computational studies[J]. Journal of Wind and Structures, 2002, 5(2/3/4): 177-192.

[4] Juretic＇ F, Kozmar H. Computational modeling of the neutrally stratified atmospheric boundary layer flow using the standard k-ε turbulence model[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2013, 115:112-120.

[5] 曾锴. 计算风工程入口湍流条件改进与分离涡模拟[D]. 上海: 同济大学, 2007.

Zeng Kai. The improvement of inlet turbulence boundary condition in CWE and detached eddy simulation[D]. Shanghai: Tongji University, 2007.(in Chinese)

[6] 杨伟, 顾明, 陈素琴. 计算风工程中的k-ε模型的一类边界条件[J]. 空气动力学学报, 2005, 23(1): 97-102.

Yang Wei, Gu Ming, Chen Suqin. A set of turbulenceboundary condition of k-ε model for CWE[J]. Acta Aerodynamica Sinica, 2005, 23(1): 97-102.(in Chinese)

[7] Yang Wei, Quan Yong, Jin Xinyang, et al. Influences of equilibrium atmosphere boundary and turbulence parameter on wind loads of low-rise buildings[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008, 96(10/11): 2080-2092.

[8] 杨伟, 金新阳, 顾明, 等. 风工程数值模拟中平衡大气边界层的研究与应用[J]. 土木工程学报, 2007, 40(2): 1-5.

Yang Wei, Jin Xinyang, Gu Ming, et al. A study on the self-sustaining equilibrium atmosphere boundary layer in computational wind engineering and its application[J]. China Civil Engineering Journal, 2007,40(2): 1-5.(in Chinese)

[9] 顾明, 李孙伟, 周印. 平衡大气边界层的数值模拟和风洞实验[J]. 同济大学学报自然科学版, 2009, 37(3): 298-302.

Gu Ming, Li Sunwei, Zhou Yin. Numerical and experimental studies on self-sustaining equilibrium atmosphere boundary layer[J]. Journal of Tongji University Natural Science, 2009, 37(3): 298-302.(in Chinese)

[10] 孙玉航, 王国砚, 王梦虹. 一类平衡大气边界层边界条件研究[J]. 力学季刊, 2015, 36(2): 328-335.

Sun Yuhang, Wang Guoyan, Wang Menghong. A boundary condition of equilibrium atmospheric boundary layers[J]. Chinese Quarterly of Mechanics, 2015, 36(2): 328-335.(in Chinese)

[11] Hargreaves D M, Wright N G. On the use of the k-ε model in commercial CFD software to model the neutral atmospheric boundary layer[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2007,95(5) : 355-369.

[12] Blocken B, Stathopoulos T, Carmeliet J. CFD simulation of the atmospheric boundary layer-wall function problems[J]. Atmospheric Environment, 2007,41(2): 238-252.

[13] Kose D A, Fauconnier D, Dick E. ILES of flow over low-rise buildings: Influence of inflow conditions on the quality of the mean pressure distribution prediction[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2011,99(10): 1056-1068.

[14] Levitan M L, Mehta K C, Vann W P. Field measurements of pressures on the texas tech building[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1991, 38(10/11): 227-234.

[15] Levitan M L, Mehta K C. Texas tech field experiments for wind loads part 1: building and pressure measuring system[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1992, 43(1/2/3): 1565-1576.

[16] Wilcox D C. Turbulence modeling for CFD[M]3rd ed. Los Angeles, USA: DCW Industries, Inc., 1994.

[17] Taghinia J, Rahman M, Siikonen T. Simulation of indoor airflow with RAST and SST-SAS models: a comparative study[J]. Building Simulation, 2015, 8(3): 297-306.

【中文责编：晨兮；英文责编：之聿】

2016-04-12；Accepted：2016-05-13

Numerical simulation of self-sustaining equilibrium atmosphere boundary layer and TTU building model

Yang Lei†, Li Lei, and Yang Xianglong

College of Civil Engineering, Shenzhen University, Shenzhen 518060, Guangdong Province, P.R.China

Constructing the equilibrium atmosphere boundary layer (ABL) is an important problem in computational wind engineering (CWE). Based on the standard k-ε turbulence model and the Richards & Hoxey inflow boundary condition, the top boundary condition is revised by adding shear stress and applied on the numerical simulation of a two-dimensional empty fetch. A fairly good boundary condition for the simulation of self-sustaining equilibrium atmosphere boundary layer is presented based on the results. The suggested boundary conditionsare also applied to the simulation of the full-scale Texas Tech University (TTU) building model with the standard k-ε model and the shear stress transport (SST) k-ε model, and a comparison is made among the numerical results and the field measurements. The simulation results prove the validity of the suggested boundary conditions.

computational wind engineering; equilibrium atmosphere boundary layer; horizontal homogeneity; standard k-ε model; top boundary condition; Texas Tech University (TTU) building model

Yang Lei, Li Lei, Yang Xianglong. Numerical simulation of self-sustaining equilibrium atmosphere boundary layer and TTU building model[J]. Journal of Shenzhen University Science and Engineering, 2016, 33(5): 470-475.(in Chinese)

TU 973.32

Adoi：10.3724/SP.J.1249.2016.05470

国家自然科学基金资助项目(11102116)；深圳市科技计划资助项目(GJHS20120621155355526)

杨磊(1978—)，男，深圳大学副教授、博士．研究方向：实验及计算流体力学．E-mail:yanglei@szu.edu.cn

Foundation：National Natural Science Foundation of China (11102116); Shenzhen Science and Technology Research Foundation(GJHS20120621155355526)

† Corresponding author：Associate professor Yang Lei. E-mail: yanglei@szu.edu.cn

引文：杨磊，李磊，杨向龙. 平衡大气边界层自保持及TTU风压数值模拟[J]. 深圳大学学报理工版，2016，33(5)：470-475.