对称分布的三轴谐振陀螺仪的设计、分析与仿真*

2016-10-21陈竟成许高斌马渊明陈兴

传感技术学报 2016年9期

关键词：陀螺仪陀螺模态

陈竟成，许高斌，马渊明，陈兴

（合肥工业大学电子科学与应用物理学院，安徽省MEMS工程技术研究中心，合肥230009）

对称分布的三轴谐振陀螺仪的设计、分析与仿真*

陈竟成，许高斌*，马渊明，陈兴

（合肥工业大学电子科学与应用物理学院，安徽省MEMS工程技术研究中心，合肥230009）

为了实现单片集成三轴陀螺仪，提出了一种完全对称的四方陀螺结构。介绍了该陀螺的结构设计及工作原理，给出了动力学简化模型，并给出了其动力学方程的详细推导。运用Ansys软件对陀螺结构进行了静态分析和模态分析，仿真结果表明，陀螺在施加100 GHz载荷下所受最大应力为1.942 MPa，陀螺各模态的固有频率分别为57.345 kHz、57.382 kHz以及57.395 kHz，各模态间匹配性能较好。对陀螺结构的仿真研究的结果表明其抗过载及模态匹配满足陀螺的设计要求。

三轴陀螺；对称；动力学分析；抗过载；模态匹配

EEACC：7230doi：10.3969/j.issn.1004-1699.2016.09.006

微陀螺广泛地应用于民用电子设备、惯性导航系统、飞行器制导与控制、汽车导航及安全、军事武器等应用中。在微陀螺的应用中，很多时候需要同时测量三个方向的角速度，传统的解决方法是将三个单轴组合成一个集成的三轴陀螺仪［1］，这种结构其体积大，功耗高，可靠性能差，因而逐渐被淘汰，转而研发可以单片集成的有单一结构组成的三轴陀螺仪。

美国ST公司开发了一种The Beating Heart结构的三轴陀螺仪［2］，该陀螺已被应用于iphone4之中，其最大量程为2 000°/s，有效工作温度在-40℃至80℃，工作电压为3.6 V，平均噪声密度小于0.03 dps/√Hz，整个芯片大小为4.4 mm×7.5 mm× 1.0 mm。意大利比萨大学的GiomiE等人开发了一种由八块板块对称分布的陀螺仪结构［3］，其噪声密度为0.1°/s√Hz，该陀螺仪采用了模拟CDMA技术，减少了模拟前段，使得硅片面积减少了24%。

目前，国内的陀螺研发集成化程度不高，主要的研究集中在单一检测轴（特别是z轴检测）微陀螺仪的设计上［4-11］，这些研究提出了一些不错的结构解耦方案，然而没有实现多轴检测的单一结构集成。东南大学的夏敦柱等提出了一种由4块大质量块及4块小质量块组合而成的三轴陀螺仪结构［12］，采用了频率调谐的方法来消除各模态间的频率差值，该频差的最终值在30 Hz以内，同时驱动和敏感模态的品质因数分别为23 816及19 507。

本文提出了一种完全对称的四方陀螺结构，其各板块完全相同且对称分布，使得各板块同步驱动。文中给出了该陀螺的结构设计、工作原理和动力学模型，利用有限元仿真软件分析了其在输入100 G载荷下的抗过载能力，对驱动模态及各检测模态进行模态仿真，实现了工作模态的匹配，从而提高陀螺的性能。

1　结构设计

图1所示为三轴陀螺仪的结构原理图。该结构由四块板块构成，四块板块绕中心锚点四方对称分布，并通过弹性梁与锚点相连，每一块板块结构均相同。

图1　三轴陀螺仪结构示意图

如图1（b）所示，四块板块可以分为两对对称的组合，每一块板块包含驱动质量块、x/y轴检测质量块、z轴检测质量块及各弹性梁，其中x轴检测质量块位于水平方向板块，而y轴检测质量块则位于竖直方向板块。每一部分的驱动质量块构成各板块的外框架，各检测质量块嵌在该外框中，并由固定在外框上的弹性梁悬挂支撑。四个板块通过折叠梁相互连接。

在驱动模态中，外框架被驱动电机驱动，并通过折叠梁互相连接，使得彼此同步运动，其中竖直方向上两块沿x轴反向驱动，另外两块沿y轴反向驱动。如图2所示，四块板块同步驱动，运动形态类似同时绕中心锚点旋转。

图2　驱动模态示意图

敏感模态包含面内及面外两种运动，4块板块均包含z轴输入敏感模态，其中竖直方向板块包含y轴输入敏感运动，而水平方向板块包含x轴输入敏感运动。当结构敏感到x/y轴方向的角速度时，x/y方向的检测质量块受到哥氏效应影响做面外差分运动，通过其下方放置的检测电极测量位移变化。相对地，当敏感到z轴方向的角速度时，检测质量块受到哥氏效应影响做面内差分运动，并通过其下方固定的叉指形检测电极测量位移变化。

图3为z轴检测结构与叉指形固定电极结构示意图，检测结构与叉指电极交叉放置，每一根叉指电极与两根检测结构交叠，检测结构与叉指电极构成差分检测电容。如图3示，当z轴检测质量块在驱动方向运动时，电极与两根检测结构交叠面积之和保持不变；当质量块在检测方向运动时，电极与检测结构交叠面积之和将随检测方向的运动而发生变化，通过该差分电容测量其检测运动位移变化。

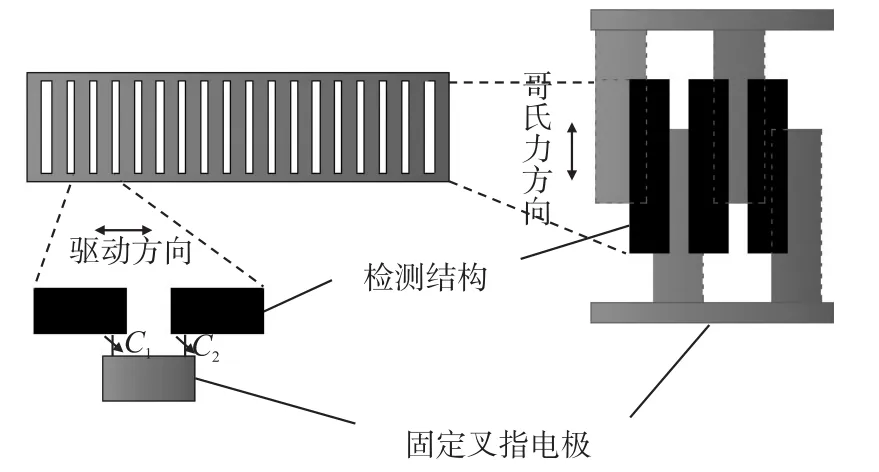
图3　z轴检测结构示意图

2　动力学分析

对陀螺的驱动和检测部分进行动力学简化。如图4所示，每一块极板均包含驱动及检测部分，单一的极板可以可以简化为一个多自由度的质量-弹簧-阻尼系统。

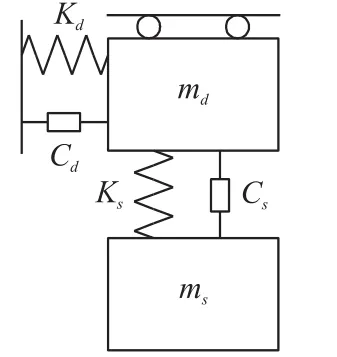
图4　整体动力学模型

图4中，md为驱动框架质量，ms为检测质量块，kd驱动方向等效弹性系数、ks为检测方向等效弹性系数，cd为驱动方向等效阻尼器的阻尼、cs为检测方向等效阻尼。

在驱动模态，由于结构对称分布，各板块所受驱动力大小相等，忽略误差干扰项，可以认为每一块板块在各自驱动方向上同步运动、位移相等。因此，单独分析其中一块板块的受力-运动关系，如图5所示。

图5　结构驱动运动的动力学模型

其驱动运动微分方程为：

式中，m1为驱动方向等效质量，c1与k1为其对应的等效阻尼与等效弹性系数，x1为驱动运动位移，fd表示驱动力，ωd为驱动力的频率，f′表示与该板块相连的两块板块对其施加的力之和，其与板块在驱动方向上位移相关，令f′=k′x，则上式变为：

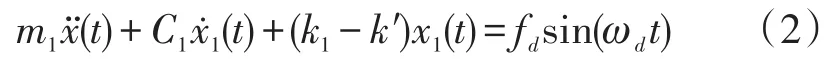
根据上式可得：

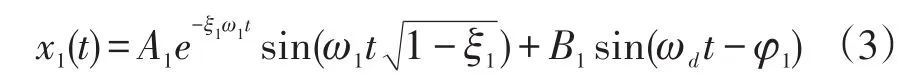
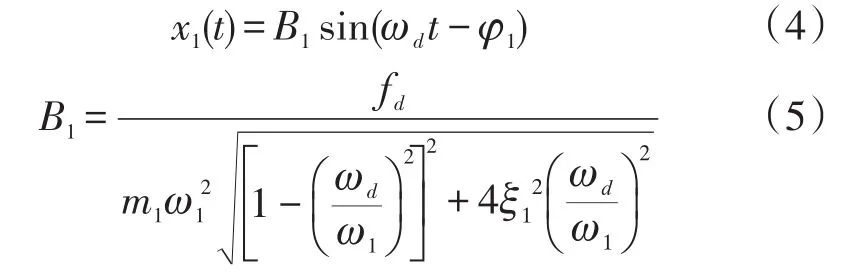
本结构中包括3个检测模态，分别为X轴、Y轴、Z轴输入对应的检测模态，3种模态均可简化为同一个质量弹簧系统，

检测运动微分方程为：

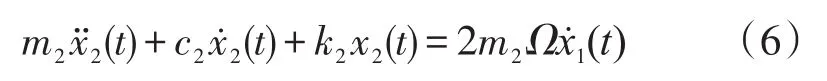
其中，m2为检测方向等效质量，c2与k2为其对应的等效阻尼与等效弹性系数，x2为检测运动位移，Ω为输入的角速度。将式（4）、式（5）带入式（6）中，求得

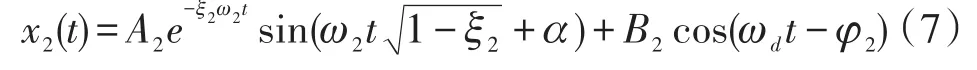
则检测运动稳态解为：

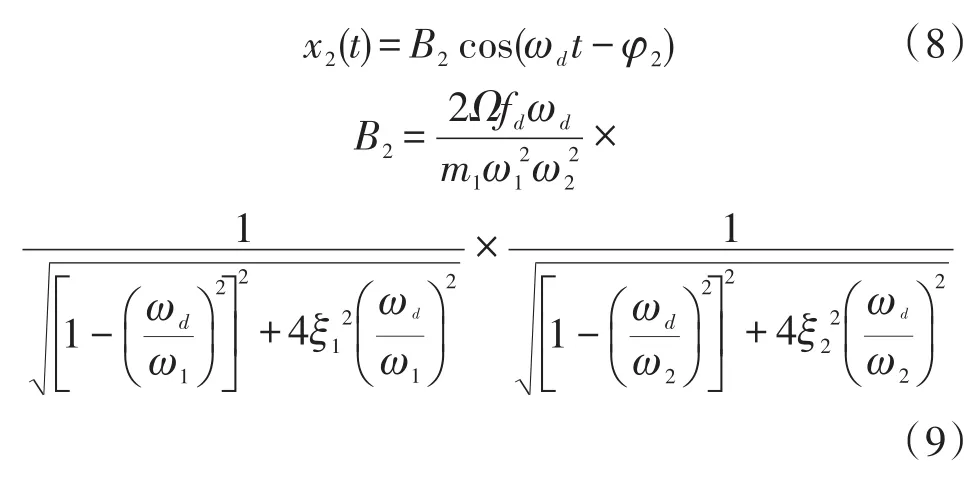
当驱动模态频率、检测模态频率及驱动频率三者相匹配时检测运动振幅最大，此时，该振动为：

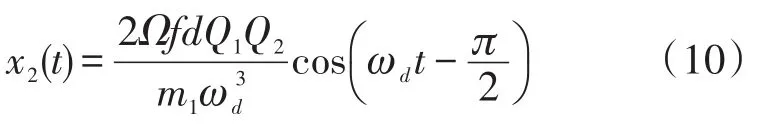
3　仿真与分析

3.1幅频分析

根据动力学相关理论，驱动力频率与驱动模态固有频率相等时，即驱动模态谐振时，该陀螺驱动模态的振幅最大。同样的，当驱动力频率与检测模态固有频率相等时，陀螺的检测模态振幅最大。而驱动模态固有频率与检测模态固有频率之间差值同样影响陀螺的检测振动振幅。

根据图6的Matlab仿真分析结果可知，陀螺在驱动模态固有频率处达到最大驱动振动频率。

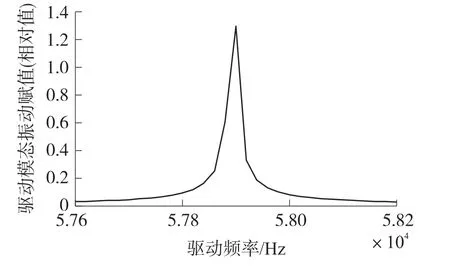
图6　驱动频率与驱动模态振幅关系

如图7所示，检测振动随驱动频率变化有两个峰谷，分别在驱动模态固有频率及检测模态固有频率处。驱动模态与检测模态固有频率差值越小，检测振动的最大振幅越大，但是当这一差值减小时，陀螺的带宽也随之减少。

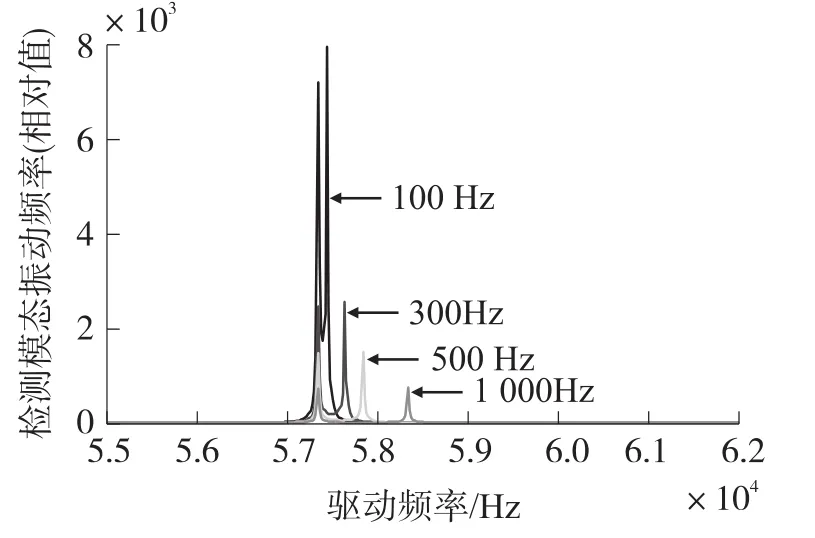
图7　驱动频率与检测模态振幅关系

3.2有限元仿真分析

3.2.1静力学分析

利用Ansys进行有限元仿真分析，采用单晶硅材料属性，设solid45单元结构。在陀螺X、Y、Z 3个方向分别施加100 G载荷，分析其结构中应力分布。

在陀螺3个方向施加100 G载荷时，其应力分布云图如图8所示，其中图8（a）、8（b）、8（c）分别为陀螺在X轴、Y轴及Z轴方向受载荷作用下的应力分布。

可以看出，结构中应力主要集中在各弹性梁和质量块及锚点等连接部分，以及弹性梁的折叠变形部分，其中3种情况下最大应力分别为900.7 kPa、986.1 kPa和1.942 MPa。

通过以上分析可以证明，本文设计的陀螺可以承受一定的冲击。单晶硅的断裂强度大于1 GPa，在100 gn载荷作用下，其结构最大应力1.942 MPa远小于结构的断裂强度，不会导致陀螺受迫损坏。

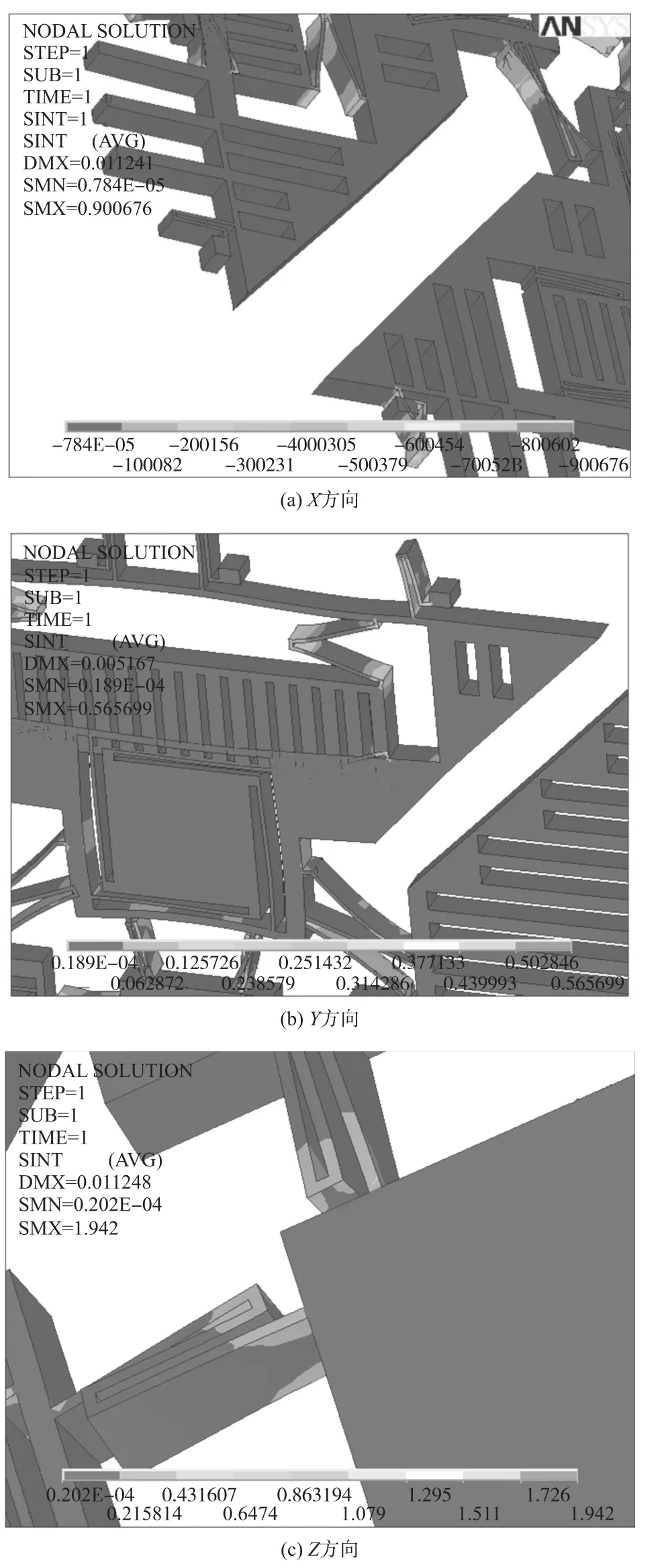
图8　各方向100G载荷下应力云图

3.2.2模态分析

陀螺各模态的谐振频率是影响陀螺性能的关键参数。图9为Ansys软件仿真下的陀螺的模态分析。

图9（a）为陀螺的面内驱动模态，驱动模态的谐振频率为57.345 kHz，在该模态中，结构的驱动模态被激励，四个板块同步进行面内运动，形态类似于绕中心锚点旋转。

该器件有4个敏感模态，分别为驱动模态，面内x轴敏感模态、面内y轴敏感模态及面外z轴敏感模态，其中，x、y轴敏感模态由于结构的对称分布，两者模态相近，在此仅列出其中之一。图9（b）、9（c）所示为各敏感模态，其中x/y轴输入引起的敏感模态谐振频率为57.382 kHz，z轴输入引起的敏感模态谐振频率为57.395 kHz。各工作模态间频率最大差值为50Hz，相比于谐振频率很小，比值约为0.087%，基本满足了陀螺对各工作模态的频率匹配要求。

图9　模态仿真

3.3陀螺性能分析

陀螺各工作模态的频率匹配除了影响灵敏度外，还决定其工作带宽的大小，陀螺的带宽约为0.54Δf，Δf指驱动模态与检测模态的频率差［13-14］。本文设计的陀螺带宽约为27 Hz，而在实际应用中，往往要求更大的工作带宽，按应用环境的不同，这一要求可以达到70 Hz，甚至100 Hz［15］。为了增大陀螺的工作带宽，同时保证较高的机械灵敏度，可以在设计陀螺的信号处理电路时对其进行处理。如在曹慧亮等人的工作中引入了偶极子补偿控制器，将陀螺的带宽从13 Hz扩展到了76 Hz［16］。

驱动结构与衬底的连接弹性梁在驱动方向上呈弹性，在其它方向上呈刚性（特别是对应的检测方向上），使得检测运动很难被传递到驱动运动上，从而削弱检测模态对驱动模态的耦合效应。检测模态对驱动模态的耦合可以表示为：

Δ为交叉耦合的相对百分量，根据上式可算得，z检测模态对驱动模态耦合为0.024%，x/y检测模态对驱动模态耦合为3.06%。

连接检测质量与驱动质量块的弹性梁在其驱动方向上呈刚性，检测方向上呈弹性，可以削弱驱动模态对检测模态的交叉耦合，同时每一组检测质量块都是对称设计，对称的两个质量块驱动方向相反，形成的检测电容变化为差分变化量，可以使驱动模态耦合到检测模态的部分相互抵消。

结合理论计算与仿真分析，可以得出该陀螺的主要性能参数理论值，如表1所示。其中品质因数取无阻尼孔，大气条件下所得值；而实际情况由于真空封装并添加阻尼孔将使得品质因数被大大提高。但是由于微结构加工工艺产生的误差及阻尼的作用，实际的陀螺性能将与计算所得具有差异，特别是品质因数（特别是x/y轴检测模态的品质因数）将比计算所得品质因数小得多。

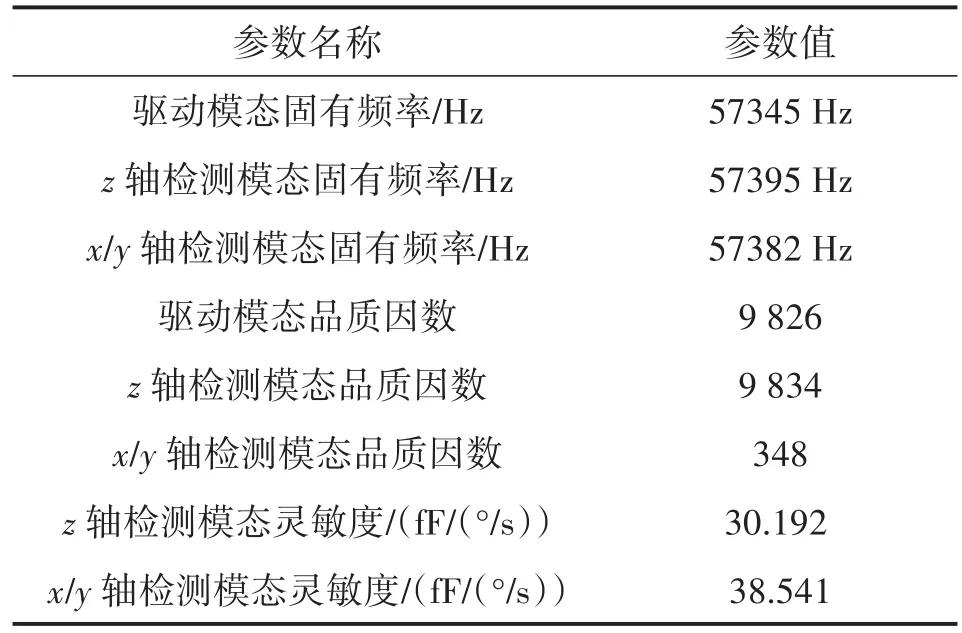
表1　陀螺部分参数理论值

4　结束语

本文设计了一种完全对称的四方陀螺结构的单片集成三轴陀螺仪，其驱动形态类似于绕中心旋转，各检测质量块对称嵌入四个方向上的驱动结构中。在分析陀螺的工作原理基础上，给出了各模态的动力学模型，并通过动力学理论计算及Matlab仿真分析明确了陀螺结构参数对性能的影响。文中利用Ansys有限元仿真软件对陀螺行了静态及模态分析，在施加100G载荷条件下，陀螺结构中最大应力为1.942 MPa，远小于结构材料的断裂强度。通过模态分析，调整陀螺结构的尺寸参数，使各模态频率匹配，其驱动谐振频率为57.345 kHz，敏感模态频率与驱动谐振频率的最大差值为50 Hz，可以有效提高陀螺灵敏度。通过理论计算，得到该陀螺z轴检测模态及x/y轴检测模态对驱动模态的交叉耦合分别为0.024%、3.06%，驱动模态、z轴检测模态及x/y轴检测模态品质因数分别为9826、9834、348，而z轴灵敏度为30.192 fF/（°/s）、x/y轴灵敏度为38.541 fF/（°/s）。研究所得结论与设计相符，表明设计是可行的。

［1］许宜申，王寿荣，王元山.单片三轴归为机械振动陀螺仪研究［J］.高技术通讯，2006，10（16）：1034-1038.

［2］Benedetto Vigna.Tri-Axial MEMS Gyroscope and Six Degree-Of-Freedom Motion Sensors［C］//InternationalElectron Devices Meet⁃ing（IEDM），2011 IEEE International，2011：29.1.1-29.1.3.

［3］GiomiE，FanucciL，RocchiA.Analog-CMDA Based Interfaces for MEMS Gyroscopes［J］.Microelectronics Journal，2014，45：78-88.

［4］谭秋林，石云波，张文栋.具有栅结构与静电梳齿驱动的电容式微机械陀螺的仿真、设计与测试［J］.纳米技术与精密工程，2011，9（3）：207-211.

［5］殷勇，王寿荣，王存超.一种双质量硅微陀螺仪［J］.中国惯性技术学报，2008，16（6）：703-711.

［6］杨晓波，李德胜，刘本东.一种微机械陀螺仪仿真分析［J］.仪器仪表学报，2006，27（6）：957-959.

［7］李博，杨拥军，徐永青.一种集成硅式硅MEMS振动陀螺仪［J］.MEMS与传感器，2013，50（8）：501-505.

［8］赵幸娟，王瑞荣，石云波.电容式硅微机械陀螺仪结构设计及仿真［J］.功能材料与器件学报，2011，17（2）：333-337.

［9］郭慧芳，李锦明，刘俊.三框架电容式硅微机械陀螺动力学分析［J］.传感器与微系统，2008，27（5）：24-26.

［10］刘梅，周百令，夏敦柱.对称解耦硅微陀螺仪结构设计研究［J］.传感技术学报，2008，21（3）：435-438.

［11］许昕，何杰，王文.微机械陀螺仪的新进展及发展趋势［J］.压电与声光，2014，36（4）：588-595.

［12］夏敦柱，孔伦，虞成.四模态匹配三轴硅微陀螺仪［J］.光学精密工程，2013，21（9）：2326-2332.

［13］陆学斌，刘晓为，陈伟平.振动式微机械陀螺的带宽特性分析［J］.传感技术学报，2008，21（2）：337-340.

［14］Cenk Acar，Andrei Shkel.MEMS Vibratory Gyroscopes Structural Approaches to Improve Robustness［M］.Springer，2009：32-35.

［15］Antonello R，Oboe R.Exploring the Potential of MEMS Gyro⁃scope：Successfully Using Sensors in Typical Industrial Motion Control Applications［J］.IEEE Industrial Electronics Magazine，2012，6（1）：14-24.

［16］曹慧亮，李宏生，申冲.基于偶极子补偿法的硅微机械陀螺仪带宽拓展［J］.仪器仪表学报，2015，36（11）：2427-2434.

陈竟成（1991-），男，安徽宿松人，硕士研究生，研究方向是MEMS传感器的设计与研究，victor0324@126.com；

许高斌（1970-），男，博士，教授，硕士生导师。现任合肥工业大学电子科学与应用物理学院教授，安徽省MEMS工程技术研究中心主任，主要从事CMOS MEMS、MEMS传感器与系统的设计、制造与封装等方面研究，gbxu@ hfut.edu.cn。

Design，Analysis and Simulation of the Symmetrical Distribution of Three Axis Resonant Gyroscope*

CHEN Jingcheng，XU Gaobin*，MA Yuanming，CHEN Xing
（Micro Electromechanical System Reaserch Center of Engineering and Technology of Anhui Province，School of Electronic Science& Applied Physics，Hefei University of Technology，Hefei 230009，China）

A square symmetrical tri-axis gyroscope structure was proposed to realize the monolithic integrated threeaxis gyroscope.Firstly，the idea of design and working principle of the gyroscope was introduced，while the dynamic model with its dynamic equation was given.Then，the structure static analysis and modal analysis was simulated by using the Ansys software.The simulation results shows that the maximum stress under the applied load of 100 GHZ under load is 1.942 MPa，while the Natural frequencies of each mode are 57.345 kHz，57.382 kHz and 57.395 kHz，which means that the matching performance between modal is good.The simulation for this gyroscope structure demonstrate that the mode matching performance and resistance to overload and meet the design require⁃ments for the tri-axis gyroscope.

tri-axis gyroscope；symmetrical；dynamic analysis；overload resistance；mode matching