悬索桥的静风扭转发散有限元精细化分析

吴长青，张志田

(湖南大学 风工程试验中心，湖南 长沙　410082)



悬索桥的静风扭转发散有限元精细化分析

吴长青，张志田†

(湖南大学 风工程试验中心，湖南 长沙410082)

基于大跨度悬索桥刚度退化及静风扭转发散的机理，选取了两个评价标准分别用以判断均匀流场和紊流场中悬索桥的刚度退化情况.在均匀流场中，由于主缆的变形形态与演变规律都很简单，因此可以选取主缆中点的竖向位移作为评价刚度退化及扭转发散的标准.当主缆中点向上的竖向位移恰好使其应力松弛时，结构将会出现扭转发散现象，这一竖向位移称为临界竖向位移.然而，在紊流场中，紊流中的脉动成分往往会引起结构显著的多模态耦合叠加的复杂响应.此时，前述的标准不再适用.为此，本文提出了一种基于识别时域范围内主缆长度的方法，即在时域范围内，当任意一条主缆的长度的最小值达到或十分接近无应力长度时，主缆将软化进而引起间歇式扭转发散.静、动力有限元分析表明，上述方法可以较好地解释大跨度悬索桥在不同流场中的扭转发散现象.

悬索桥；扭转发散；刚度退化；评价标准；有限元分析

对于大跨度悬索桥而言，静风扭转失稳可能先于动力失稳出现.因此，大跨度悬索桥必须具备良好的静风稳定性能.扭转发散概念来源于航空工程学中机翼的静风扭转发散现象，即机翼的扭转变形随着风速的逐渐增加而缓慢增加，当风速达到某一值时，扭转变形急剧跃增至一个很大的程度而导致结构发生破坏[1-2].Simiu与Scanlan在大跨度桥梁抗静风研究中首次引用了这一概念，并提出了一种简单估算主梁扭转发散临界风速的线性方法[3]，但是它是基于线性假定而提出的，忽略了所有的非线性效应，这显然不能准确地评估桥梁的静风稳定性能.

为了考虑非线性因素的影响，Boonyapinyo等提出了一种静力有限位移法来分析大跨度斜拉桥的耦合屈曲问题[4-5].不久，Chen等采用此方法对大跨度悬索桥的静风失稳问题进行了研究[6-7].在这些研究中，均采用了静力有限元方法，并考虑了结构的几何非线性、材料非线性及风荷载非线性的影响.需要提出的是，静力有限元方法可以较好地揭示桥面扭转发散的机理与发展的全过程，但是无法考虑紊流引起的随机响应对扭转发散的影响.众所周知，大气边界层附近的流场都是紊流.因此，有必要采用动力有限元方法来探究紊流对大跨度悬索桥静风扭转发散的影响.

已有研究表明，随着作用在结构上向上荷载的逐渐增减，主缆系统将会出现软化现象，这表明向上的运动对结构的刚度会产生不利的影响[8].为了讨论紊流的影响，张志田等采用了动力有限元方法研究了一座大跨度悬索桥的静风稳定性[9].结果表明，紊流引起的随机动力响应明显地降低了桥梁的静风稳定性能.但是大跨度悬索桥的静风扭转发散机理那时依然不清楚.后来.张志田等基于风洞试验成果并建立了广义梁-索分析模型，较好地揭示了大跨度悬索桥扭转发散的本质原因是主缆系统扭转刚度的退化[10-11].对于大跨度悬索桥而言，结构体系的扭转刚度主要来源于由两根主缆组成的主缆系统而不是桥面[12].因此，当主缆系统的扭转刚度退化后，桥面极易在风荷载的作用下发生扭转破坏.

本文基于大跨度悬索桥刚度退化及静风扭转发散的机理，采用静、动力有限元分析方法分别研究了均匀流场及紊流场中矮寨大桥的静风稳定性能，并提出了这两种流场各自适用的刚度退化的评价标准.在均匀流场中，由于主缆的变形形态与发展规律明确且易于描述，因此可以选取主缆中点的临界竖向位移作为评价标准.当任意一条主缆向上的竖向位移达到临界值时，主缆将发生软化并致使主缆系统丧失了绝大部分的扭转刚度，这一过程即为刚度退化过程.刚度退化后，桥梁结构只残余主梁提供的扭转刚度.然而这一部分刚度很容易被风速引起的气动扭转负刚度抵消，最终导致桥面发生扭转破坏.本文采用静力有限元的方法求解了临界竖向位移值，并评估其他一些响应对该临界值的影响.然而，在紊流场中，脉动风将会引起结构显著的随机动力响应，主缆的响应也变得十分复杂.此时，前述的标准将不再适用.为此，本文提出了一种基于识别时域范围内主缆长度的方法，即在时域范围内，当任意一条主缆的长度的最小值达到或十分接近无应力长度时，主缆将发生软化而使得桥面出现间歇式扭转发散现象.本文将采用动力有限元分析方法并结合这一标准来解释紊流场中大跨度悬索桥扭转发散特性.

1　扭转发散机理

基于梁-索广义模型，Zhang等阐述了大跨度悬索桥的扭转发散机理[11].根据已有的成果可知，主缆系统的广义扭转刚度(KTc)为：

(1)

式中：Kc1,Kc2分别为迎风面主缆与背风面主缆的广义竖向刚度；B为两根主缆之间的水平距离.此外，主梁贡献的扭转刚度为：

(2)

当不考虑材料非线性时，这部分刚度将为恒值.

梁-索体系的广义扭转刚度KT则为KTc与KTb之和：

(3)

由公式(3)可知，只有当Kc1,Kc2都大于零时，即两根主缆都受拉时，主缆系统才提供扭转刚度.也就是说，当任意一条主缆发生软化，系统刚度将大部分丧失甚至完全丧失(刚度退化过程).此时，梁-索体系的扭转刚度几乎只剩下主梁提供的扭转刚度(KTb).对于大跨度悬索桥而言，主缆系统的KTc一般远大于主缆的KTb[11-12].根据这一受力特性，公式(3)可以更具体化为：

此外，风速引起的广义气动扭转刚度KTα也可由文献[10]得到：

(5)

式中：ρ为空气密度，U为风速，Cm为主梁断面的升力矩系数，α为风速攻角，α0为初始风速攻角.

在刚度退化前，结构体系的扭转刚度由公式(4a)计算，它足以抵抗气动扭转刚度而使桥面不易出现扭转发散.然而在刚度退化后，则由公式(4b)计算，显然残余的扭转刚度往往难以抵抗气动扭转负刚度而致使桥面发生扭转发散，因此刚度退化是大跨度悬索桥静风扭转发散的关键原因[11].此外，扭转发散临界风速定义为致使主缆系统扭转刚度退化所对应的风速，描述为：

(6)

式中：ε为主缆的应变，u，v，w分别为紊流场中3个方向的脉动风速，对于均匀流场而言，脉动风速取零.

2　刚度退化的评价标准

由文献[11]的理论分析可知，主缆的应变是主缆垂度的函数.当主缆垂度减小至一个临界值时，主缆应变将为零，此时主缆系统的扭转刚度将会退化.主缆垂度的减小是升力作用所致的向上竖向位移的结果.因此，可以将以垂度表达的刚度退化条件转换为以主缆中点的竖向位移来表达.在不考虑主缆侧向响应与桥塔塔顶响应的情形下，可以定义刚度退化对应的临界竖向位移值为：

Vcr=f*-f0

(7)

式中：f*为成桥状态下主缆的静态垂度值，f0为无应力垂度.需要说明的是，式(7)表达的临界竖向位移值是在只考虑主缆竖向响应且振型函数近似假定为二次抛物线型的前提下才适用的.基于广义模型由公式(7)计算得到的Vcr值称为临界竖向位移的理论值.

在均匀流场中，由于主缆响应的发展过程比较简单，且变形前后主缆线型均可以近似假定为二次抛物线型，因此可以将公式(7)中Vcr作为均匀流场中大跨度悬索桥刚度退化的评价标准.值得提出的是，在实际情况下，这一临界竖向位移值还会受到主缆的侧向响应与桥塔塔顶的顺桥向响应的影响.本文3.2节将采用静力有限元求解矮寨大桥在均匀流场中的临界竖向位移值，并评估上述两种响应对临界值的影响.

然而在紊流场中，脉动风会引起结构显著的多模态耦合的动力响应.此时，主缆的线型无法近似用一个具体的解析式来描述，因此得不到系统扭转刚度的显式表达式.公式(7)所述的临界竖向位移不再适合作为紊流场中刚度退化评价标准.由文献[11]可知，主缆的应变与主缆的长度增量有关，这里提及的主缆长度增量为响应后主缆的长度与主缆无应力长度的差值.当主缆长度等于无应力长度(即长度增量为零)时，主缆应变为零，即相当于主缆系统的扭转刚度也为零.由此启发，本文将在动力有限元分析中识别出时域范围内主缆的长度，并以时域范围内主缆长度的最小值等于或接近无应力长度L0作为紊流场中刚度退化的评价标准.该标准具体描述如下：

在动力有限元时域分析中，t时刻主缆的长度按下式计算：

(8)

式中：N为主缆被划分的单元数目，Δxi(t)，Δyi(t)，Δzi(t)分别为i单元沿x，y，z坐标轴方向的长度.

因此，紊流场中刚度退化的评价标准可写成：

min [L(t)]=L0

(9)

式中：min [L(t)]为时域范围内主缆长度的最小值，L0为主缆的无应力长度.需要说明的是，这个标准的成立在一定程度上依赖于时域分析的时间长度，时间长度取得越长，主缆刚度退化的可能性越大，这似乎使得此标准变得模糊.但庆幸的是，大跨度悬索桥的静风失稳问题本质上也是一个基于风场随机特性的概率性问题，因此在时域分析中合理地取了一个时间长度即可.本文3.3节将采用动力有限元方法分析紊流场中大跨度桥梁的扭转发散特性，并验证这一标准的合理性.

3　有限元分析

3.1工程概况

以矮寨大桥为有限元算例.矮寨大桥为一座山区峡谷大跨度悬索桥，采用钢桁架梁方案.桥梁主跨1 176 m，加劲梁全长1 000.5 m；主缆矢跨比1∶9.6，两条主缆形心距27 m；梁高7.5 m，桁架节间距7.25 m.全桥布局如图1所示.表1列出了矮寨大桥的主要计算参数.图2为全桥ANSYS有限元模型，采用的是单主梁模型，共有471个节点和687个单元.图3给出了加劲梁断面的静力三分力系数.计算时主梁上同时施加阻力、升力与升力矩，静力三分力系数按图3取值；主缆上只施加阻力，阻力系数取0.8.

图1　全桥布置图

图2　全桥有限元模型

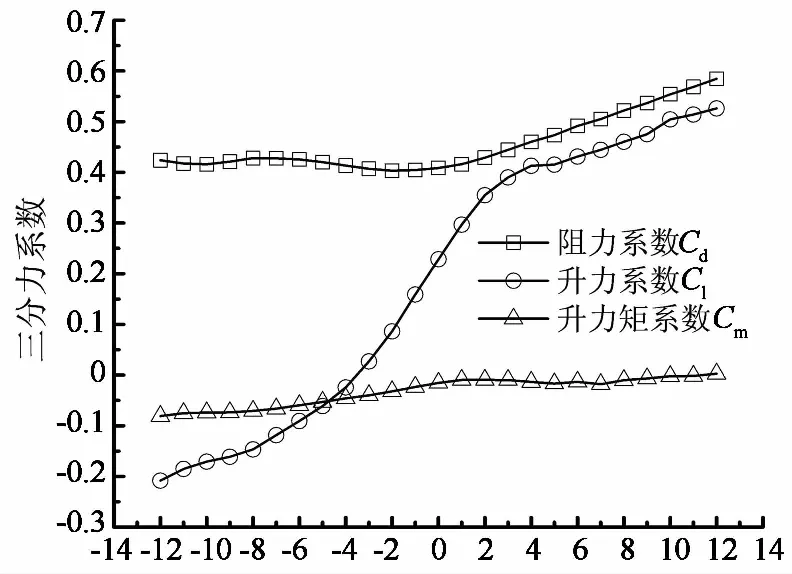
风攻角/(°)

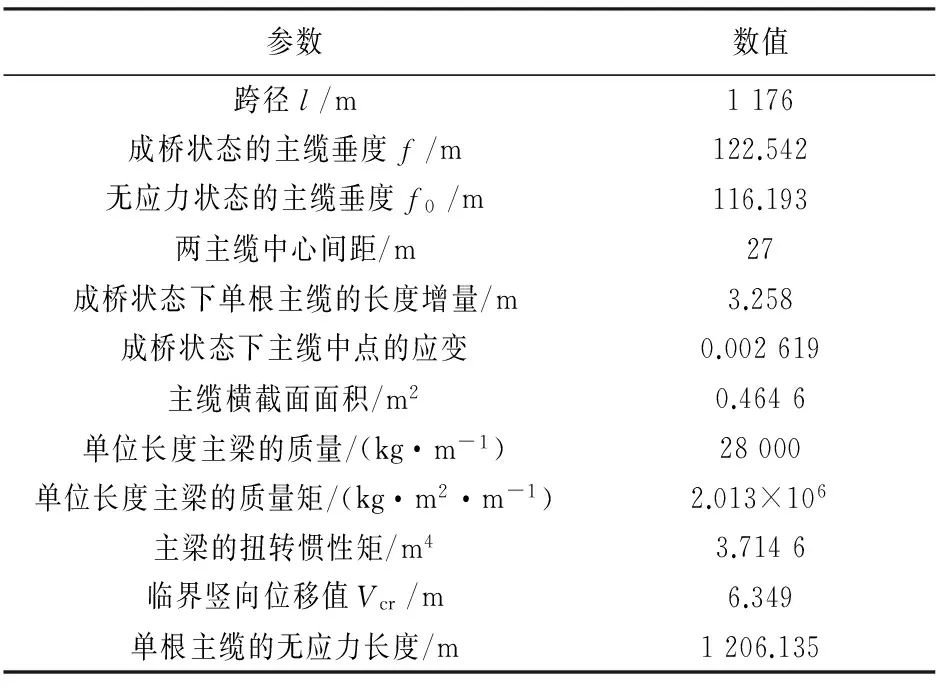
参数数值跨径l/m1176成桥状态的主缆垂度f/m122.542无应力状态的主缆垂度f0/m116.193两主缆中心间距/m27成桥状态下单根主缆的长度增量/m3.258成桥状态下主缆中点的应变0.002619主缆横截面面积/m20.4646单位长度主梁的质量/(kg·m-1)28000单位长度主梁的质量矩/(kg·m2·m-1)2.013×106主梁的扭转惯性矩/m43.7146临界竖向位移值Vcr/m6.349单根主缆的无应力长度/m1206.135

3.2静力有限元分析

基于ANSYS软件采用静力有限元方法研究均匀流场中大跨度悬索桥的扭转发散特性.计算中考虑了结构的几何非线性及风荷载非线性效应，忽略了材料非线性效应，且初始风速攻角均取0°.为了评估其他响应对临界竖向位移值的影响，本文构造了几种具有不同约束条件的有限元模型，模型的描述及其对应的数值结果见表2.

表2　几种模型的描述及对应的数值结果

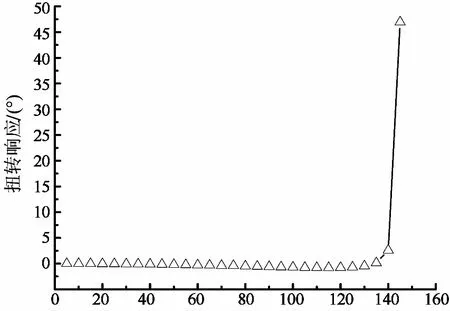
表3给出了实际模型(情形F)在不同平均风速作用下主缆中点的竖向响应均值及主梁中点的扭转响应值.图4分别为情形F对应的迎风面主缆中点的竖向响应曲线和主梁中点的扭转响应曲线.由图4可知，风速从140 m/s增至145 m/s的过程中，竖向响应与扭转响应均出现了明显的跃增现象，这表明结构正经历失稳破坏过程，这种情况下的临界失稳风速可定为140 m/s.由表3可知，临界竖向位移值为12.634 m，大于临界竖向位移的理论值(6.349 m)，这表明有限元计算得到的临界竖向位移值还受到结构其他响应的影响.

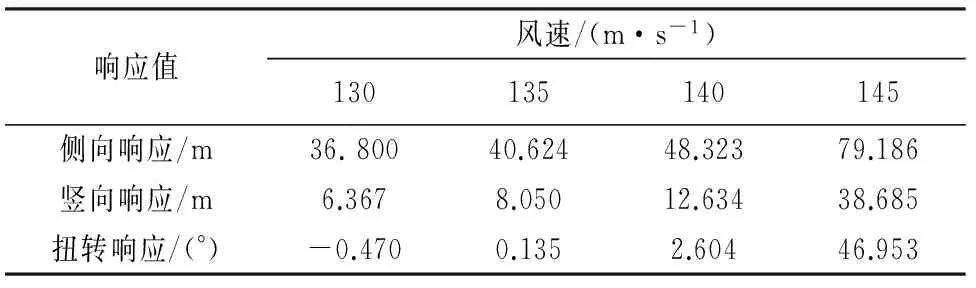
表3　实际模型(情形F)在不同风速作用下中点的响应值

注：表中竖向、侧向响应为迎风面主缆中点的，扭转响应为主梁中点的

需要说明的是，临界竖向位移的理论值是基于广义梁-索模型得到的，为了简化该模型没有考虑主缆的侧向响应及桥塔塔顶的响应.然而在有限元计算中，这两种响应均存在.因此，不妨猜想是这两种响应导致了上述临界竖向位移计算值与理论值之间出现了偏差.

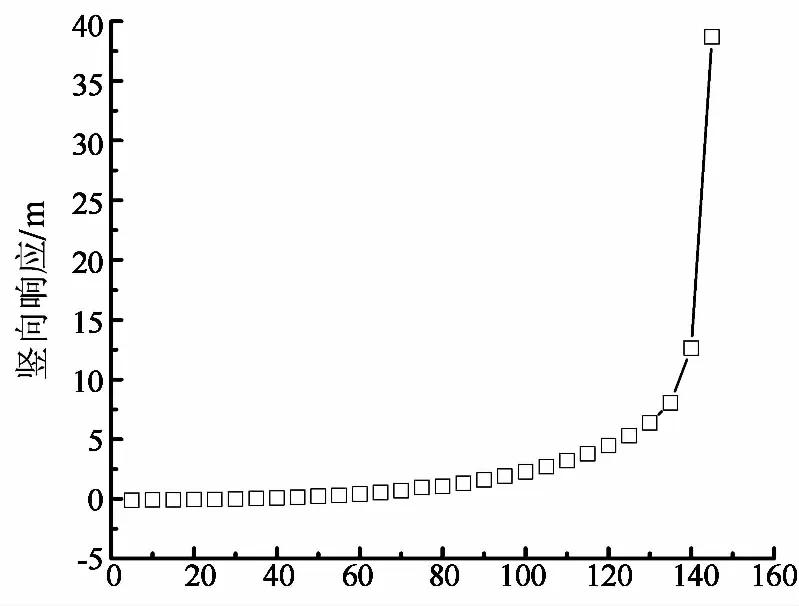
风速/(m·s-1)

风速/(m·s-1)

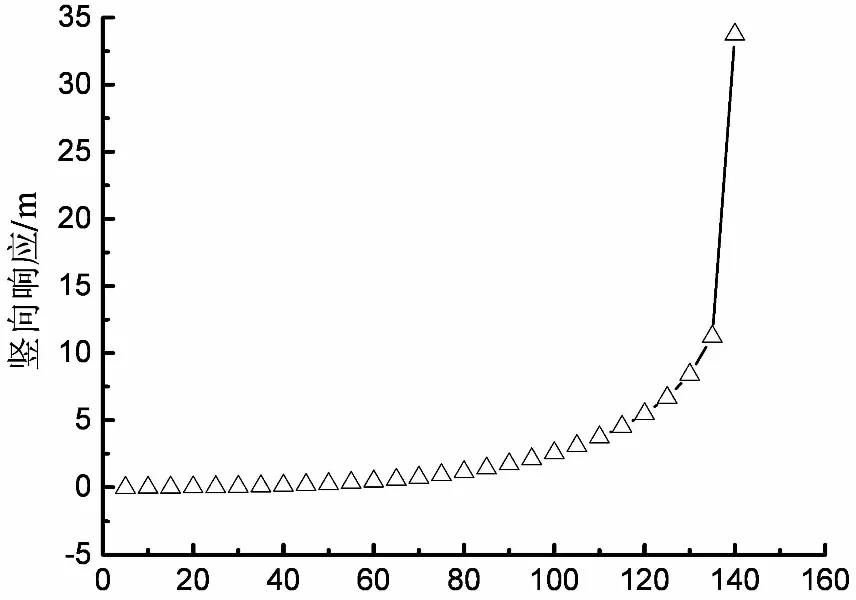
对于情形A中的新模型1，它是在实际结构的有限元模型上，约束主缆的侧向自由度和桥塔塔顶的顺桥向自由度而得到的.对该模型进行数值计算得到的结果如下：图5(a)为迎风面主缆中点的竖向响应曲线，图5(b)为主梁中点的扭转响应曲线.由图5(a)可识别出这种情形下的临界竖向位移为6.386 m，与广义模型预测的理论值相当接近，这表明之前的猜想是正确的.

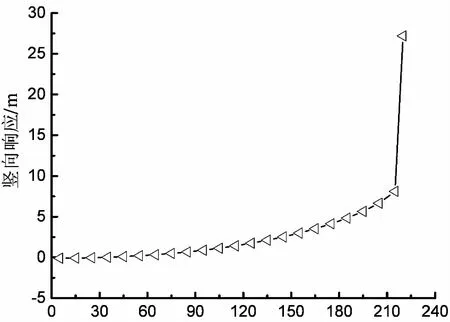
对于情形B中的新模型2，它是在实际结构的有限元模型上，约束桥塔塔顶的顺桥向自由度而得到的；对于情形C中的新模型3，它是在实际结构的有限元模型上，约束主缆的侧向自由度而得到的.这两种情形对应的数值结果分别在图6及图7中显示.由表3可知，情形B对应的临界竖向位移值为11.233 m，相比理论值大4.884 m.情形C对应的临界竖向位移值为8.119 m，相比理论值大1.770 m.这表明主缆的侧向响应和桥塔塔顶的顺桥向响应均可以在不同程度上延缓刚度退化，提高临界竖向位移值.

由扭转发散机理可知，向上的竖向位移引起的主缆系统刚度退化是悬索桥静风扭转发散的主要原因.鉴此，通过约束主梁竖向自由度来限制主缆的竖向响应的措施应当可以提高结构的静风稳定性能.采取措施后的有限元分析结果如图8所示，当风速高达200 m/s以上时，主梁的扭转响应仍然比较小，未出现扭转发散的迹象.比较图8与图4(b)可知，降低主缆竖向响应的措施可以有效地提高结构的静风稳定性能.

风速/(m·s-1)　　　　　　　　　　　　　　　　　　　　风速/(m·s-1)

风速/(m·s-1))　　　　　　　　　　　　　　　　　　　　风速/(m·s-1)

风速/(m·s-1))　　　　　　　　　　　　　　　　　　　　风速/(m·s-1)

风速/(m·s-1)

3.3动力有限元分析

采用动力有限元法研究紊流场中大跨度悬索桥的扭转发散特性.采用谐波合成法[13-15]模拟得到了桥梁一系列离散位置处的随机脉动风速时程.模拟时取B类场地，衰减指数取0.16，粗糙高度取0.05 m，目标风速功率谱按《公路桥梁抗风设计规范》的建议取Kaimal谱.模拟得到的脉动风速时程，其顺风向紊流强度为0.19左右，竖风向紊流强度为0.10左右.计算中考虑了结构的几何非线性及风荷载非线性效应，忽略了材料非线性效应.

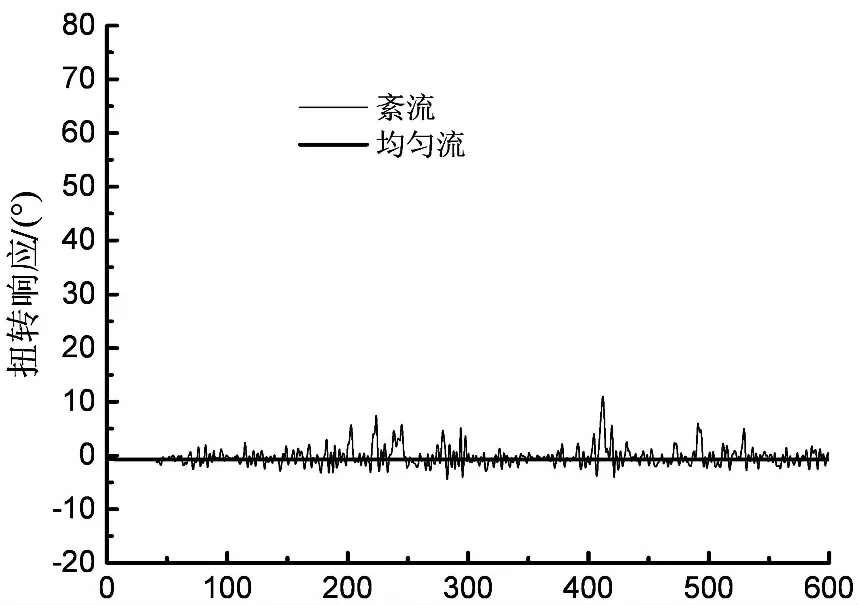
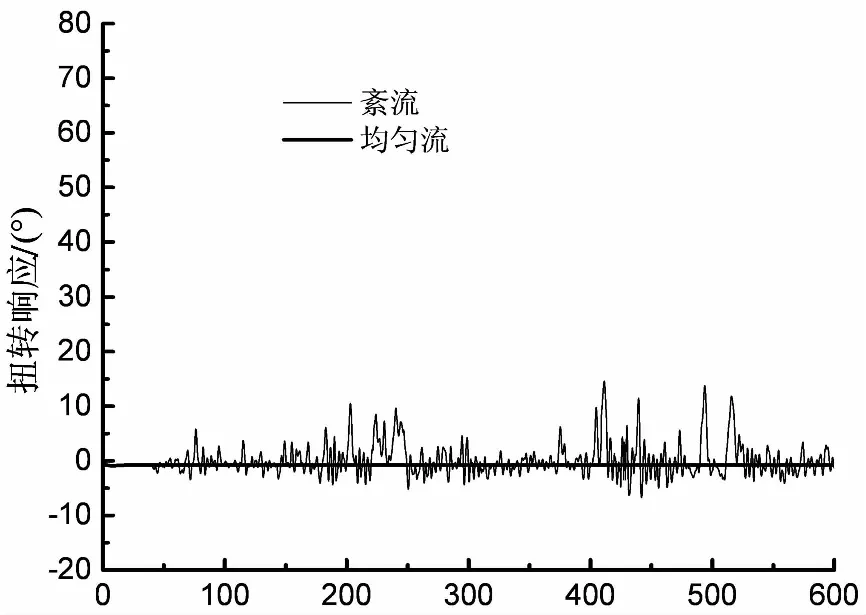
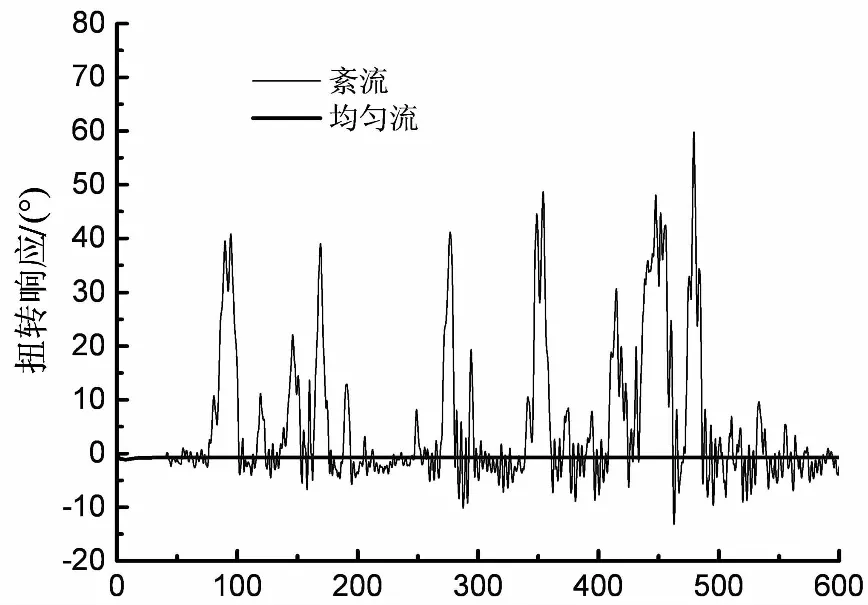
图9为0°攻角下三种风速时程下主梁中点的扭转响应时程曲线.由图可知，扭转峰值响应在风速由105 m/s增至110 m/s的过程中出现了十分显著的跃增现象.110 m/s风速情形下的最大扭转响应峰值达到60°，且绝大部分峰值都大幅度偏离在均匀流曲线上方，这表明当风速等于或超过110 m/s时，主梁将进入间歇式扭转失稳状态.据此，可以确定矮寨大桥在紊流场中的临界失稳风速为105 m/s.

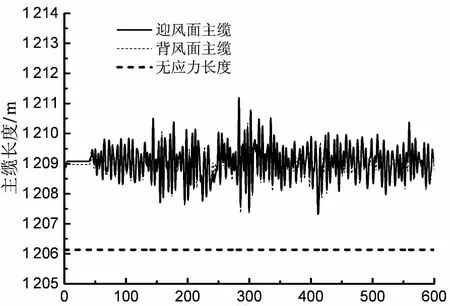
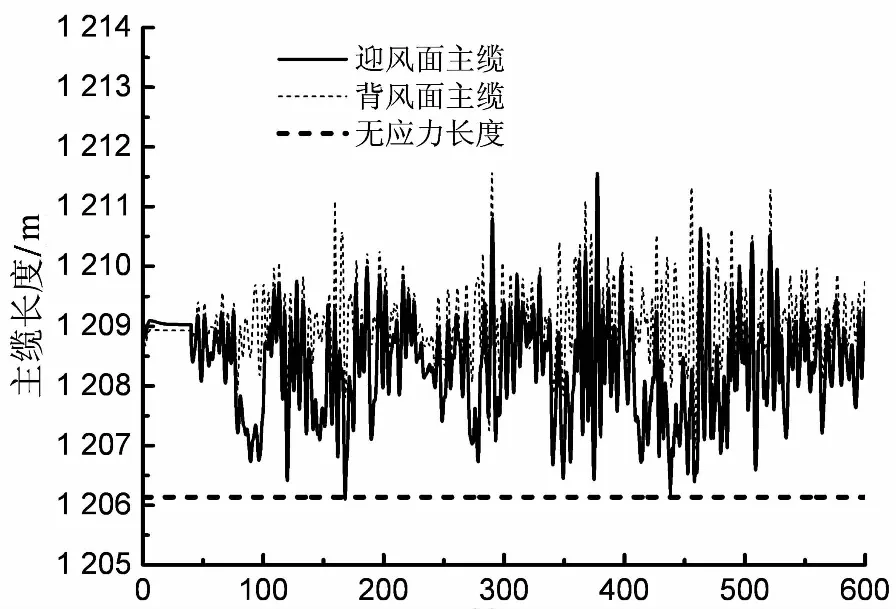
图10分别给出了三种不同风速时程下的主缆长度时程曲线.通过观察曲线变化规律，可以归纳以下两点：1)对于风速为100 m/s与105 m/s的情形，无论是迎风面主缆还是背风面主缆，主缆长度的变化幅度均不是很大，而且其低峰值均位于无应力长度曲线的上方较高位置处，由此可知两根主缆的长度增量均大于零且较大.这表明两根主缆的应力均较大，主缆系统的扭转刚度也较大，因此主梁的扭转响应较小，结构处于稳定的振动状态.2)对于风速为110 m/s的情形，背风面主缆的长度总体上要比迎风面主缆的长度要长，这表明结构体系的平均扭转角为抬头力矩方向.此外由图可知，迎风面主缆长度的低峰值已经十分接近无应力长度，即时域范围内主缆长度的增量已经趋近于零，这意味着迎风面主缆出现了间歇式软化现象，主缆系统的扭转刚度大幅度降低，桥面主梁出现显著的间歇式扭转发散现象，如图9(c)所示.从时域范围内主缆长度时程曲线角度分析，也可以确定矮寨大桥在紊流场中的扭转发散临界风速为105 m/s.这表明公式(9)所描述的临界风速与刚度退化评价标准是适用并可靠的.

时间/s

时间/s

风速/(m·s-1)

时间/s

时间/s

时间/s

在时域范围内选取了5个时刻，从主缆全长的角度展现并分析这些时刻的竖向响应及侧向响应情况.

由上述分析可知，风速为105 m/s时，结构未出现刚度退化及扭转发散现象，主缆的竖向响应中主要包含少数低阶振型，因此主缆的竖向振型表现为比较规则的正对称形态或反对称形态，如图11所示.此外，由此图也可知主缆的竖向响应也较小，这表明主缆的拉应力较大，主缆系统仍然具有较大的扭转刚度.然而，当风速为110 m/s时，桥面已经出现了显著的间歇式失稳现象.无论是迎风面主缆还是背风面主缆，其竖向响应较大而且线型变得比较复杂没有规则，如图12所示.这可以归因于主缆的刚度退化，由于主缆出现了显著的软化，其高阶振型很容易被风速时程激起，从而使得更多的高阶振型也参与到竖向响应中来.

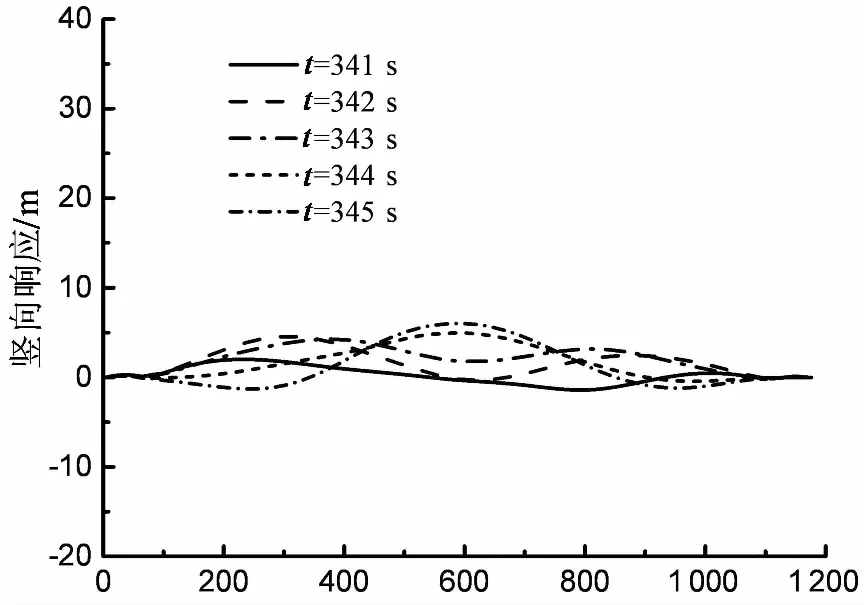
顺桥向坐标/m

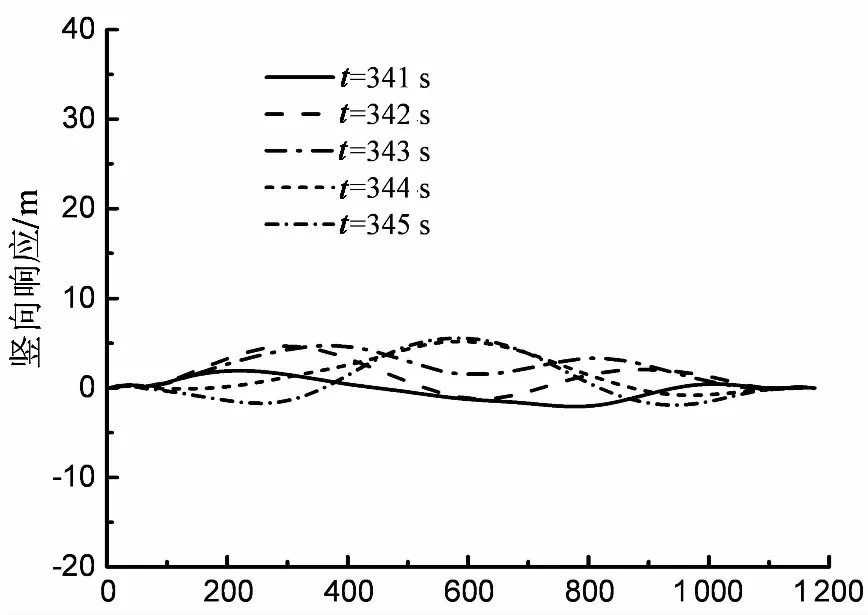
顺桥向坐标/m

对于主缆的侧向变形而言，也有类似的规律.当风速为105 m/s时，主缆的侧向响应较小，而且侧弯振型表现为规则的正对称抛物线型，如图13所示.然而，当风速达到110 m/s时，由于主缆系统扭转刚度的大幅度降低，侧向响应明显增大，同时一些较高阶侧弯振型也参与进来，使得侧向振型变得不规则，不同时刻的侧向响应曲线出现了相互交织的现象，如图14所示.

表4简要总结了大跨度悬索桥扭转发散及刚度退化研究的成果.由表可知，紊流场中悬索桥的扭转发散临界风速远低于均匀流场中的临界风速.这表明紊流引起的抖振响应大大降低了桥梁的静风扭转稳定性能.

图12　U =110 m/s激励下主缆的竖向响应

图13　U =105 m/s激励下主缆的侧向响应

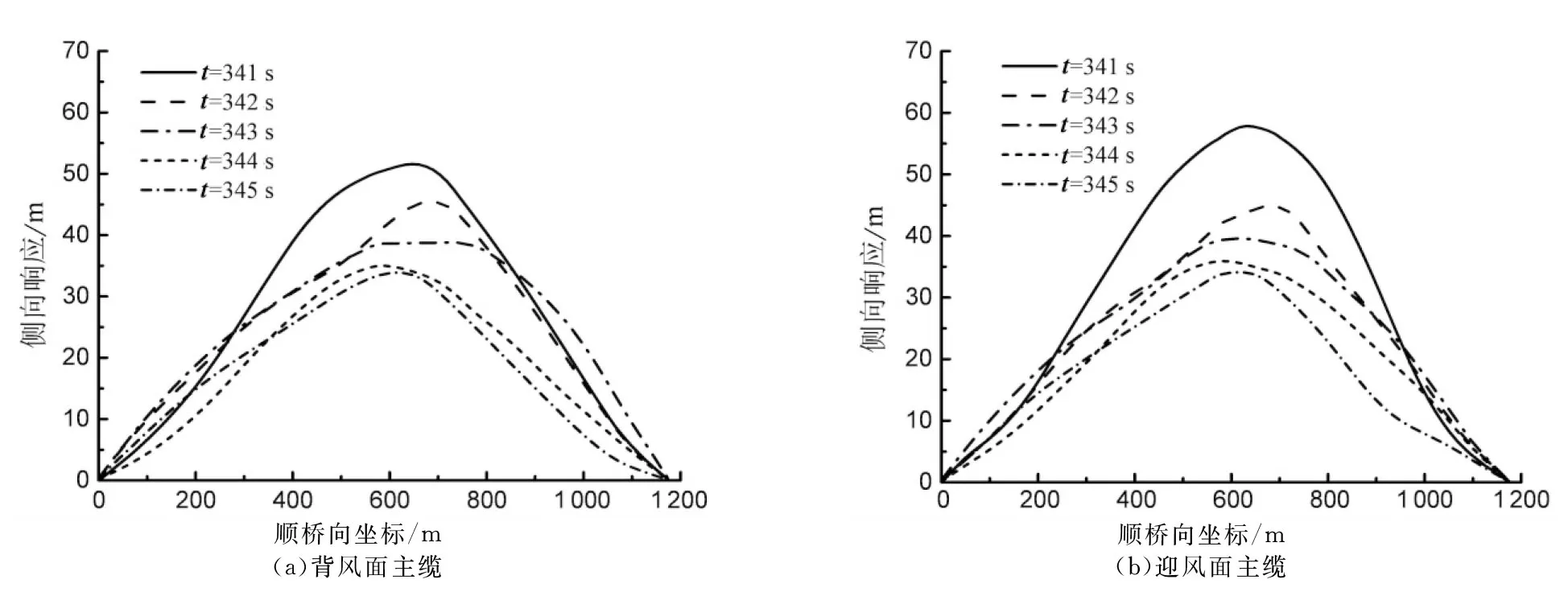
图14　U =110 m/s激励下主缆的侧向响应

表4　两种流场中的静风扭转发散对比

4　结　论

本文分别采用静、动力有限元方法研究了大跨度悬索桥在均匀流场及紊流场中的扭转发散特性与刚度退化的评价标准，研究结果总结如下：

1)对于均匀流场，选取主缆中点的临界竖向位移作为刚度退化的评价标准.求解了主缆刚度退化对应的临界竖向位移并研究了主缆侧向响应及桥塔顶部响应对临界竖向位移的影响.静力有限元结果表明，主缆侧向响应及桥塔顶部顺桥向响应可以在一定程度上延缓主缆的应力松弛，提高临界竖向位移值.

2)对于紊流场，通过识别时域范围内主缆的长度，并以时域范围内主缆长度的最小值达到无应力长度作为刚度退化的评价标准.动力有限元结果表明，当主梁发生扭转发散时，迎风面主缆的长度低峰值已经十分接近无应力长度，验证了此评价标准的适用性与可靠性.

3)静、动力有限元分析的结果表明，在均匀流场中，大跨度悬索桥的扭转发散形式具有突发性的，而在紊流场中表现为间歇式的.相同平均风速下，紊流场的结构响应比均匀流场大得多；脉动风引起的随机动力响应大幅度降低了大跨度悬索桥的静风稳定性能.

[1]陈政清.工程结构的风致振动、稳定与控制[M].北京: 科学出版社,2013：124-128.

CHEN Zheng-qing.Wind induced vibration,stability and control of engineering structure [M].Beijing: Science Press,2013：124-128.(In Chinese)

[2]DOWEL E H,CLARK R.A modern course in aeroelasticity [M].Dordrecht: Kluwer Academic Publishers,2004：327-328.

[3]SIMIU E,SCANLAN R H.Wind effects on structures-an introduction to wind engineering [M].Hokoben: John Wiley&Sons,1992：308-312.

[4]BOONYPINYO V,YAMADA H,MIYATA T.Wind induced nonlinear lateral torsional buckling of cable-stayed bridge[J].Journal of Structural Engineering,ASCE,1994,120(2):486-506.

[5]BOONYAPINYO V,LAUHATANON Y,LUKKUN-APRASIT P.Nonlinear aerostatic stability analysis of suspension bridges [J].Engineering Structure,2006,28(3):793-803.

[6]CHEN Jin,JIANG Jian-Jing,XIAO Ru-Cheng,et al.Advanced aerostatic stability analysis of cable-stayed bridges using finite element method [J].Computers and Structures,2002,80:1145-1158.

[7]CHEN Jin,JIANG Jian-jing,XIAO Ru-cheng,et al.Series method for analyzing 3D nonlinear torsional divergence of suspension bridges[J].Computers and Structures,2003,81(5):299-308.

[8]ARENA A,LACABONARA W.Nonlinear parametric modeling of suspension bridge under aeroelastic forces [J].Nonlinear Dynamics,2012,70:2487-2510.

[9]ZHANG Zhi-tian,CHEN Zheng-qing,HUA Xun-gang,et al.Investigation of turbulence effects on torsional divergence of long-span bridge by using dynamic finite element method[J].Journal of Bridge Engineering,ASCE,2010,16(6):639-652.

[10]张志田,张伟峰.悬索桥在紊流风场中的静风扭转发散机制[J].土木工程学报,2013,46(7):74-81.

ZHANG Zhi-tian,ZHANG Wei-feng.Mechanism of aerostatic torsional divergence of suspension bridges in turbulent flows[J].China Civil Engineering Journal,2013,46(7):74-81.(In Chinese)

[11]ZHANG Zhi-tian,GE Yao-jun,YANG Yong-xin.Torsional stiffness degradation and aerostatic divergence of suspension bridge decks[J].Journal of Fluids and Structures,2013,40:269-283.

[12]项海帆,葛耀君.悬索桥跨径的空气动力极限[J].土木工程学报,2005,38(1):60-70.

XIANG Hai-fang,GE Yao-jun.On aerodynamic limit to suspension bridges [J].China Civil Engineering Journal,2005,38(1):60-70.(In Chinese)

[13]DEODATIS G.Simulation of ergodic multivariate stochastic process [J].Journal of Engineering Mechanics,ASCE,1996,122(8):778-787.

[14]吴长青，张志田，陈政清.悬索桥静风扭转发散的影响因素研究[J].湖南大学学报：自然科学版，2016,43(3)：15-22.

WU Chang-qing,ZHANG Zhi-tian,CHEN Zheng-qing.Research of influencing factors on aerostatic torsional divergence of suspension bridges[J].Journal of Hunan University: Natural Sciences,2016,43(3):15-22.(In Chinese)

[15]罗俊杰,韩大建.大跨度结构随机脉动风场的快速模拟方法[J].工程力学,2008,25(3):96-101.

LUO Jun-jie,HAN Da-jian.A fast simulation method of stochastic wind field for long-span structures[J].Engineering Mechanics,2008,25(3):96-101.(In Chinese)

Refined Analysis of Finite Element for Torsional Divergence of Suspension Bridges

WU Chang-qing,ZHANG Zhi-tian†

(Wind Engineering Research Center,Hunan Univ,Changsha，Hunan410082,China)

On the basis of the mechanism of stiffness degradation and torsional divergence in long-span suspension bridges subjected to static wind,two criterions have been reasonably chosen for the evaluation of torsional divergence in smooth flows and turbulent flows,respectively.In a concerned bridge immersed in smooth flows,taking into account the easy estimation of the deformation conformation and the simple evolution rule of main cables,the vertical displacement at the mid-location of main cables was adopted as a criterion to estimate the stiffness degradation and torsional divergence.When the vertical displacement reaches a critical value,the phenomenon of aerostatic torsional divergence will occur.In the case of turbulent flows,however,the bridge structure will experience complicated and stochastic dynamic responses in a form of multiple modal coupling.Consequently,the criterion used in smooth flows is not applicable to this case.To this end,a new criterion based on the identification of the length of the main cables in time domain was put forward.The criterion can be described as that,when the minimum value of the main cable length indentified in the whole time domain reaches the value being equal to or very close to the zero-strain length,the bridge will be affected by the intermittent torsional divergence because of the softening of the main cable subsystem.It is shown that,using some static and dynamic finite element analyses,the phenomena of the aerostatic torsional divergence behavior of long-span suspension bridges in different types of field flows can be well explained with this new criterion.

suspension bridges；torsional divergence；stiffness degradation；evaluation criterion；finite element analysis

1674-2974(2016)09-0088-10

2015-10-09

国家自然科学基金资助项目(51178182),National Natural Science Foundation of China(51178182)

吴长青(1987-)，男，江西吉安人，湖南大学博士

†通讯联系人，E-mail:zhangzhitian999@126.com

U448.25

A