曲拐弯扭耦合振动影响规律研究

陈宏威　向建华　刘　帅　吴斌辉（北京理工大学机械与车辆学院北京100081）

·振动·噪声·

曲拐弯扭耦合振动影响规律研究

陈宏威向建华刘帅吴斌辉
（北京理工大学机械与车辆学院北京100081）

基于圆盘非对称转子简化模型和达朗贝尔原理，建立了曲轴单拐弯-扭耦合非线性振动数学模型，并利用解析推导法和四阶龙格库塔的迭代数值求解方法研究了弯曲振动和扭转振动间的相互影响规律。研究结果表明，弯曲振动（或扭转振动）会耦合产生多种频率成分的扭转振动（或弯曲振动），耦合振动幅值随着激励频率和偏心距的增加而加大，且弯曲振动对扭转振动的耦合影响相对较大。

曲拐弯扭耦合振动非线性振动影响规律

引言

内燃机曲轴应用范围广泛，结构复杂，功能繁多，是内燃机系统关键部件［1］。曲轴承受周期性变化的切向力和法向力作用，常常产生弯曲振动、扭转振动及二者的耦合振动形式，很容易引发多种振动问题，导致轴段的疲劳损坏、轴承磨损以及工作噪声等［2］。以往人们关于内燃机曲轴的研究主要集中于轴的扭转振动，但近年来随着认识的深入，一些学者开始着重关注扭转—弯曲耦合振动，形成了比较完备的理论分析、数值模拟与实验研究相结合的体系［3-5］。由于曲轴高速回转时的质量不平衡或系统不对称等非线性因素，使得数值仿真中曲轴弯曲振动的数学建模和求解比较复杂［6-8］，其相应的曲轴弯扭耦合振动分析的相关文献目前尚不多见。李慧珍［9］在有限元计算曲轴振动中将曲轴视为圆截面梁和变截面矩形梁的组合；梁兴雨［10］等建立了由多个自由度组成的发动机刚柔耦合多体动力学系统模型；何成兵［11］推导了三类微元轴段的弯扭耦合振动微分方程组，提出数值计算解法。Nataraj C［12］利用摄动的方法得到了非线性弯扭耦合振动微分方程组的初步解；梁明轩［13］分别通过谐波平衡法与数值积分法得到系统幅频特性，分析了质量偏心和转速对轴系非线性动力学响应的影响；刘占生［14］得到了共振区弯曲振动和扭转振动的频率特征，分析了不平衡量对弯扭耦合共振区的影响。目前，对于内燃机曲轴的振动耦合分析，大多是基于计算精度较差的离散质量或分布参数模型，且弯扭耦合振动影响等理论研究不够深入。

本文针对某内燃机曲轴单拐，并基于圆盘非对称转子简化模型和达朗贝尔原理，建立了曲拐弯-扭耦合非线性振动数学模型，并利用解析推导和龙格库塔的迭代数值求解方法深入研究了弯曲振动和扭转振动间的相互影响规律，从而为内燃机曲轴弯扭耦合研究提供理论指导。

1　非线性弯扭耦合模型建立和求解

对于截取的曲拐，在考虑扭转振动的前提下，采用离散化模型分析弯曲振动运动状况。将曲轴单拐简化为一个刚性圆盘并安装在具有弯曲和扭转弹性而无质量的轴上。假定轴是各向同性，两端轴承为刚性支撑，忽略了圆盘的陀螺效应，进而将整个曲拐简化为一个单质量圆盘转子模型，如图1所示。

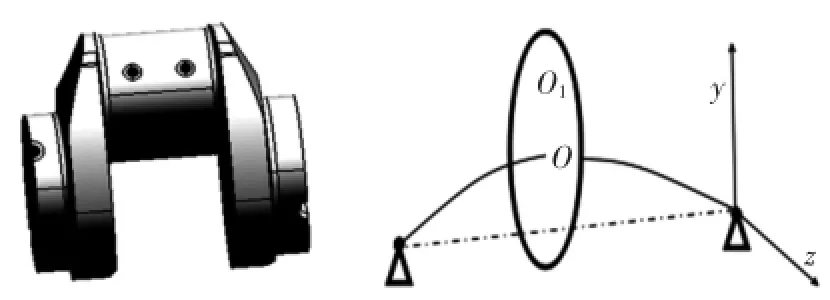
图1　曲拐和简化后的单质量圆盘转子模型

建立考虑扭转振动耦合影响和偏心距的单质量圆盘转子示意图如图2所示。圆盘旋转中心为O，质心为O1，偏心距为e，φ为质心旋转的角度，ω为转动角频率，即φ=ωt+θ，θ为扭转角。

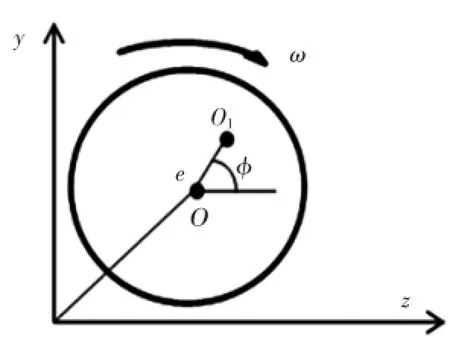
图2　圆盘转子示意图

由于偏心距e的存在，圆盘具有回转速度φ˙和回转加速度，使得质心上有切向加速度eφ¨和法向加速度eφ˙2φ¨，如图3所示。由此产生的惯性力为：

图3　惯性力分析示意图

同理，质心具有弯曲加速度y¨和z¨，产生的惯性力为-my¨和-mz¨，由此施加在回转中心的额外扭矩为：

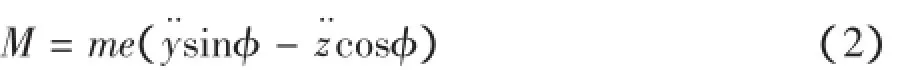
在假设圆盘为刚体且左右支撑轴弯扭各向同性的前提下，根据达朗伯原理得到弯扭耦合振动平衡方程组：式中：T为作用在曲柄销处的切向力产生的扭矩；Fy、Fz为作用在曲柄销处的径向力在y、z方向的投影；c和k为弯曲阻尼和刚度，此处不再考虑y和z方向的各向异性；ct和kt为扭转阻尼和刚度。

从式（3）定性分析可以看出，耦合振动的产生是由于偏心距e的存在，e越大耦合作用就越大。而当e=0时，圆盘的弯扭耦合振动平衡方程组变成：

即当偏心距不存在时，弯曲扭转振动间不存在明显的耦合关系。

式（3）所示的弯扭耦合振动平衡方程组中变量z、y、θ均为时间的函数，呈现高度非线性。本文利用Matlab/Simulink搭建式（3）所对应的弯扭耦合振动平衡方程组仿真模型（如图4所示），并基于四阶-龙格库塔法（Runge-Kutta）迭代求解，获得相应的数值解。

图4中，左右两边是模型输入和输出模块，浅灰色的是两个弯曲振动和1个扭转振动计算模块，深灰色的是弯扭和扭弯耦合计算模块。仿真求解时，将初始值（作用力或力矩）赋给对应的振动计算模块，得到的值经由各耦合模块计算获得新的耦合力或是力矩，再一并输入作为总激励来计算下一轮的值。以此反复迭代求解，直至满足收敛条件，从而实现弯扭耦合振动平衡方程组的数值求解。

由于弯扭耦合影响是相互的，本文在分析弯扭耦合振动作用时，采用单独控制一种振动而激发另一种振动的办法，即通过单独施加力或是力矩，观察一种振动产生时另一种振动频域下的幅值变化，从而获得弯扭振动之间的耦合作用规律。

图4　弯扭耦合振动求解模型

2　弯曲振动对扭转振动的影响研究

由式（3）可以看出，由于偏心距e的存在，弯曲振动在圆盘上产生了额外扭矩M，即M=me（y¨sinφz¨cosφ），而重力作用产生的额外扭矩大小为megsin（tω+θ）。对M进行傅立叶变换，将y、z方向的弯曲振动分解为若干简谐振动的叠加，得到：

式中：ωi为第i个弯曲振动分量的振动角频率；Yi、Zi分别为y、z两个方向上振动的振幅；αi、βi为各自的相位。

将第i分量代入M=me（y¨sinφ-z¨cosφ），得到频率为ωi的额外扭矩：

从式（6）可以看出，角频率为ωi的弯曲振动可以引起角频率为ωi±ω的扭转振动；弯曲振动产生的额外扭矩的幅值与不平衡量me成正比，与弯曲振幅（Yi，Zi）成正比，与该谐分量下角频率的平方成正比，弯曲振动相位角（αi，βi）对扭矩的幅值影响也较大。此外，由于重力作用也会产生额外扭矩，其大小为meg sin（ωt+θ），故重力会引起角频率为ω的扭转振动。

取单位曲拐模型仿真计算的基本参数为：转速为3 000 r/min，即转动频率为50 Hz，k=1.736×1010N/m，J=0.045 kg·m2，kt=1.285×106（N·m）/rad，e= 0.02 m，m=9.07 kg，弯曲激励频率为35 Hz，幅值大小为Fy=1.0×107N，Fz=5×105N，c=80（N·s）/m，Ct=100（N·m）/rad，通过图4的数值迭代计算，结果如图5所示。

从图5可以看出，在激励力35 Hz作用下，弯曲振动在35 Hz产生了明显的波峰。同时，在扭转振动的15 Hz、50 Hz、85 Hz附近产生较为明显的峰值；耦合作用产生的扭转振动幅值和弯曲振动幅值比（无量纲）为1∶40。扭转振动在15 Hz和85 Hz下产生的峰值符合│ω±ωi│的规律，即为激励力频率与转动频率之差或之和的绝对值。50 Hz处的峰值产生是因为重力所导致的不平衡引起的，重力可以产生meg sin（ωt+θ）的额外扭矩进而引起频率为ω的扭转振动。值得注意的是，虽然由弯曲振动产生的扭矩M通过傅里叶变换可以得出N个不同角频率的简谐振动，进而引起相应的一系列的扭转振动；但只有峰值较为明显（通常是低阶）的弯曲振动，耦合产生的扭转振动才较为明显。其余情况下产生的扭转振动可以忽略。

此外，在转速一定的情况下，随着弯曲振动激励力频率从55 Hz到90 Hz的变化，扭转振动幅值也呈一定的变化。其中图6显示了│ω-ωi│扭转振动随着激励力ω变化关系。

从图6中可以看出，随着弯曲振动激励力频率从55 Hz到90 Hz的变化，频率│ω-ωi│扭转振动幅值逐渐增加。因为根据公式（6）可知，弯曲振动耦合产生的额外扭矩大小的决定因素中有激励力频率，且与其平方成正比，同时受重力产生的旋转扭矩的影响，但总体上扭转振动会随着激励力频率的增加而相应的增加。特别指出，当扭转固有频率和弯曲固有频率都不大时，会出现由于弯曲振动耦合作用所导致的扭转共振的情况发生。

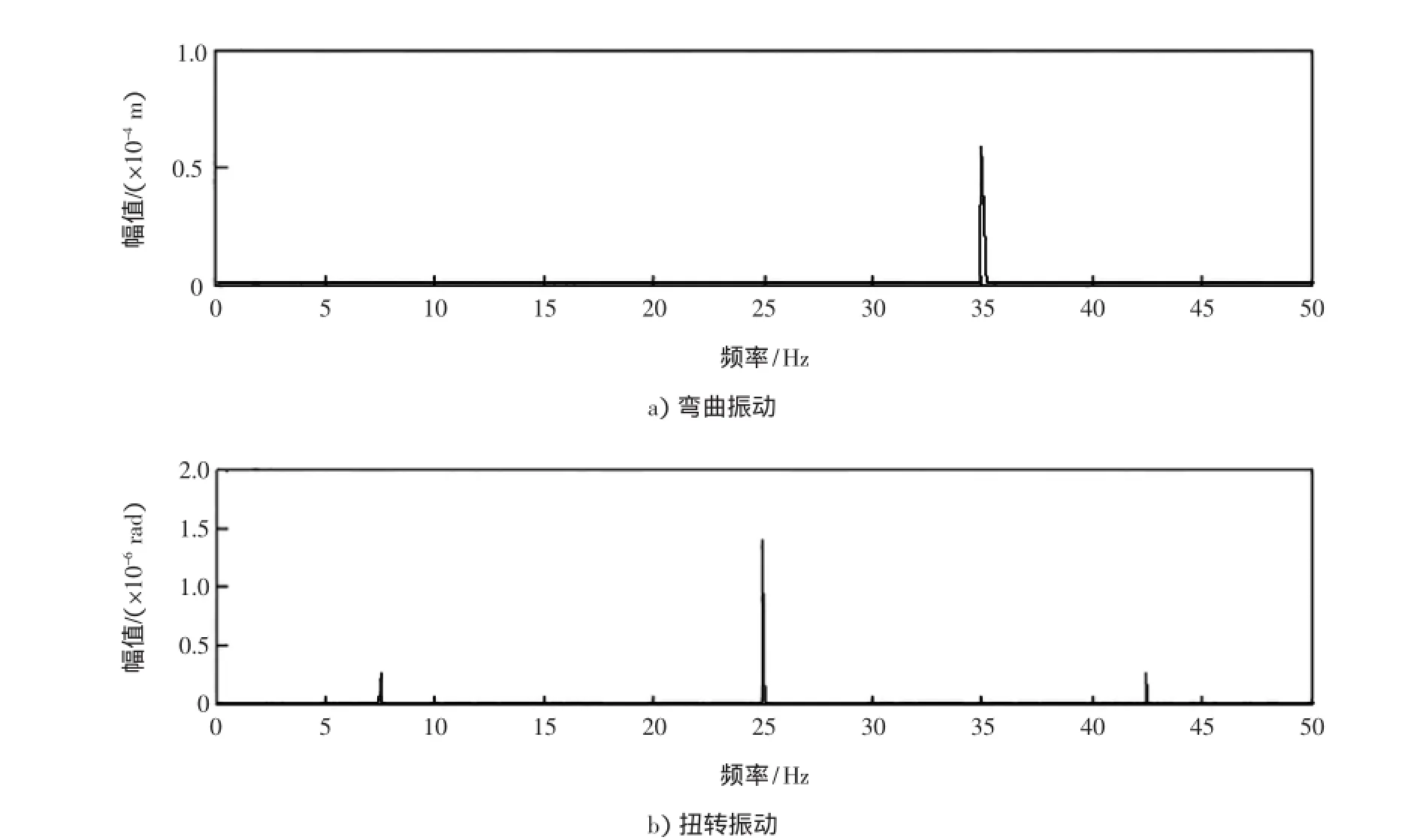
图5　弯曲振动和耦合产生的扭转振动频域图

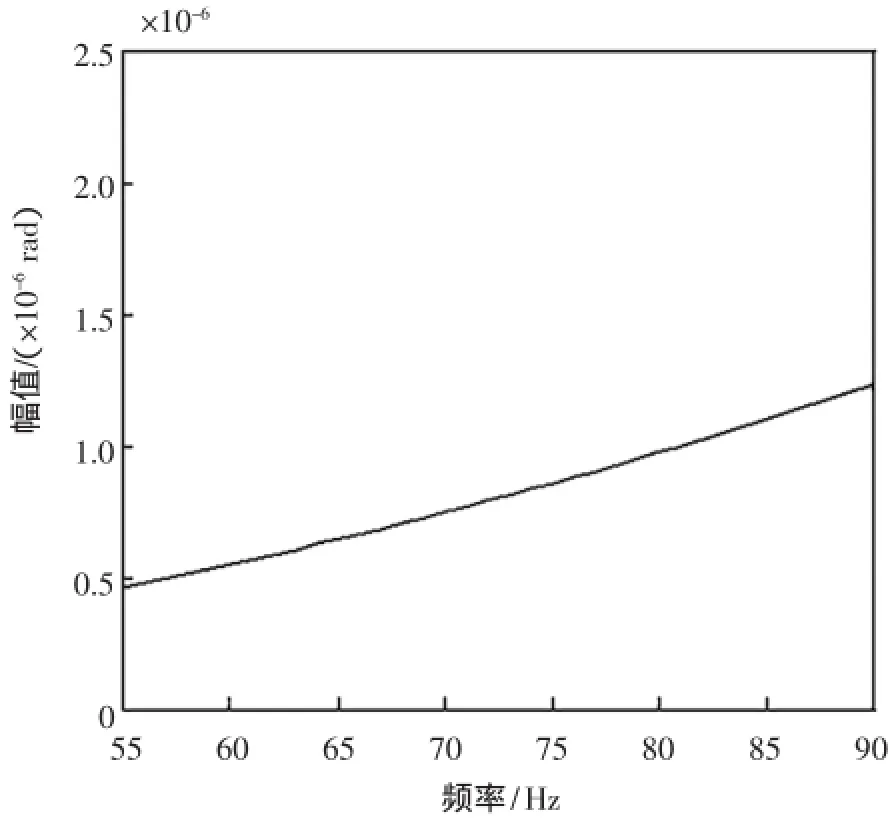
图6　│ω-ωi│扭转振动随着激励力ω变化关系

3　扭转振动对弯曲振动的影响研究

由式（3）可以看出，由于存在偏心距和扭转角的原因，在圆盘部产生了切向力和法向力，这些激励力作用在弯曲振动方向，使其产生相应的弯曲振动。这里，以Z方向弯曲振动为研究对象；为进一步分析微分方程，可以把扭转角θ分解为若干谐振动的和，即

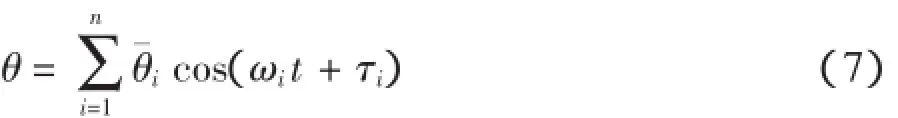
扭对弯耦合项Z方向力me（φ˙2sinφ-φ¨cosφ）进行分析，即：

式中：第1项是由于旋转不平衡引起的，为传统的不平衡弯曲振动响应激励力，它将引起同频率的弯曲振动。后边各项均是由于扭转振动引起的离心激励力，频率为：

1）ω±ωi，幅值与、不平衡me、转速ω成正比，与ωi或是成正比。

3）ω±ωi±ωj，幅值与乘积、不平衡me、ωiωj乘积成正比。

4）2ωi±ω，幅值与、不平衡me成正比。

通过对比可知，这些激励力由于幅值引入了扭振角，扭转振动引起的惯性力相比不平衡直接引起的同频率弯曲振动幅值要小很多；而其中ω±ωi频率下对应的振幅相对大一些。

同样，取单位曲拐模型仿真计算的基本参数为：转速为3 000 r/min，即转动频率为50 Hz，k=1.736× 1010N/m，J=0.045 kg·m2，kt=1.285×106（N·m）/rad，e=0.02 m，m=9.07 kg，扭矩频率为35 Hz，幅值大小为T=2e4N·m，c=80（N·s）·m-1，ct=100（N·m·s）·rad-1。通过图4的数值迭代计算，结果如图7～图9所示。

图7　扭转振动频域图

图8　耦合引起的同频率弯曲振动幅值

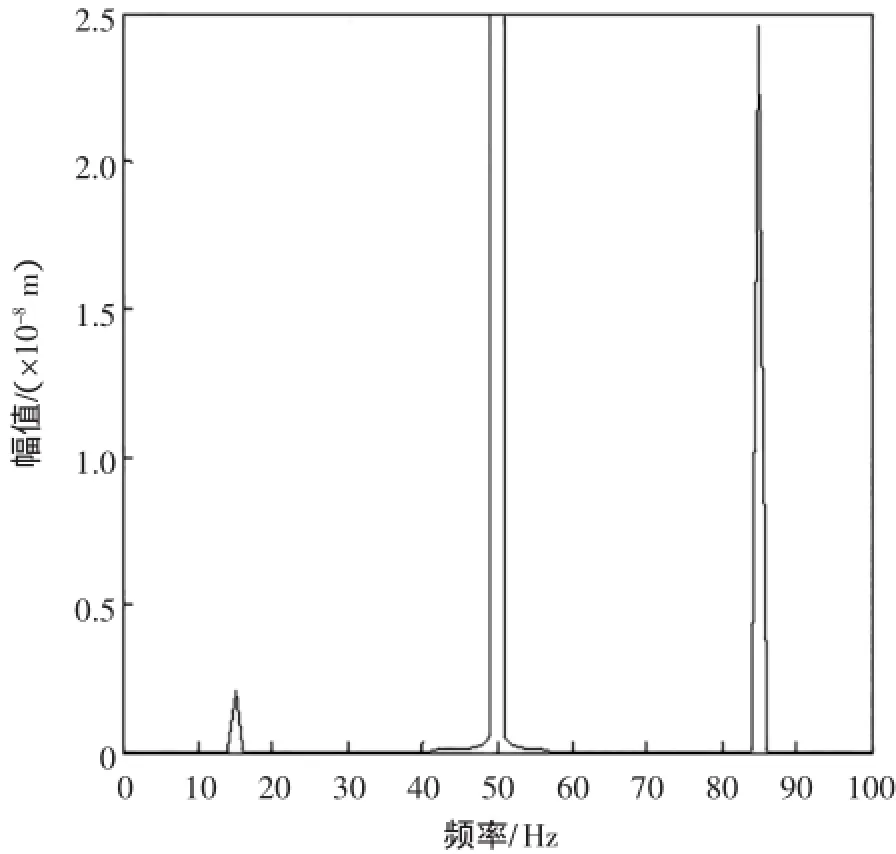
图9　耦合引起的ω±ωi频率弯曲振动幅值

从图7可以看出，在35 Hz扭矩的作用下，产生了比较明显的波峰；图9中弯曲振动在15 Hz、50 Hz和85Hz附近产生了明显的波峰；耦合作用产生的弯曲振动幅值和扭转振动幅值比（无量纲）为1∶12 000。图8中在弯曲振动50 Hz处产生明显峰值的原因是传统的同频弯曲振动作用的结果，其幅值与不平衡成正比，与转速ω平方成正比。图9中弯曲振动在15 Hz和85 Hz处产生峰值的原因与│ω±ωi│相符合，即是转动角频率与扭转振动频率之差或之和，其幅值与不平衡me成正比，与转速ω成正比，与ωi或是ω2i成正比，与θi成正比。由于这里的扭转刚度很大，故θi一般比较小，使得幅值要远小于同频率引起的弯曲振动；而其它频率成分对应的幅值更小，耦合作用不明显，可以忽略。

图10和图11描述了在轴系转速频率为50 Hz，外扭矩频率从55 Hz逐渐增加到90 Hz时，扭转振动引起的│ω±ωi│频率的弯曲振动随着外扭矩频率的变化趋势。随着扭转激励力频率的增加，弯曲振动逐渐增加，这与弯曲振动对扭转振动的结论相似。

图10　Y向弯曲振动随扭振频率的变化

图11　Z向弯曲振动随扭振频率的变化

4　结论

本文建立了曲轴单拐弯-扭耦合振动的数学模型，并针对弯-扭耦合振动和扭-弯耦合振动的影响规律进行了解析推导和数值迭代求解，计算结果具有很好的一致性。具体结论如下：

1）弯曲振动（或扭转振动）会耦合产生多种频率成分的扭转振动（或弯曲振动），都包括频率为ω±ωi的振动成分。

2）耦合产生的振动幅值随着激励频率和偏心距的增加而加大。

3）无量纲下的弯扭耦合幅值比远大于扭弯耦合幅值比，故本曲轴单拐的弯曲振动对扭转振动的耦合影响相对较大。

1Fuchun Ren，Kun Yang，Zhong Guang Fu，et al.Study on the coupling of the bending and vibrations of the unbalanced rotor［C］：Xi'an：Proceedings of the 2nd International Conference on Hydrodynamic Bearing-rotor System Dynamics，March 20-22，1997

2李震，桂长林，孙军.内燃机曲轴轴系振动分析研究的现状、讨论与展望［J］.内燃机学报，2002，20（05）：469-474

3Nevsan S.Performance increase in turbo molecular pumps with curved type blades［J］.Vacuum，2012，86（11）：1764-1769

4韩建鑫，王炜，张琪昌.内燃机曲轴系统变惯量公式的修正［J］.内燃机学报，2014，32（03）：271-275

5Munawar I，Abdul W，Dimitri B，et al.Design modification in rotor blade of turbo molecular pump［J］.Nuclear Instruments and Methods in Physics Research A，2012，678：88-90

6张勇，蒋滋康.轴系弯扭耦合振动的数学模型［J］.清华大学学报（自然科学版），1998（08）：115-118

7周桐，徐健学，傅卫平.弯扭耦合振动对次同步谐振响应的影响［J］.应用力学学报，2000，17（1）：12-17

8王雪娇.内燃机曲轴弯扭耦合非线性振动分析［D］.天津：天津大学，2009

9李慧珍，张德平.用有限元进行曲轴扭转振动计算［J］.内燃机学报，1991，9（2）：157-162

10梁兴雨，舒歌群，李东海，等.基于柔体曲轴多体动力学的轴系扭振响应分析［J］.内燃机工程，2007（04）：46-49

11何成兵，杨昆，顾煜炯.质量偏心对碰磨转子弯曲振动和扭转振动特性的影响［J］.中国电机工程学报，2002，22（7）：105-110

12 Nataraj C.On the Interaction of Torsion and Bending in Rotating Shafts［J］.Journal of Applied Mechanics，1993，60（3）：239-241

13梁明轩，袁惠群，赵天宇，等.内燃机曲轴轴系弯扭耦合非线性振动响应［J］.东北大学学报（自然科学版），2014（03）：402-405，414

14刘占生，崔颖，黄文虎，等.转子弯扭耦合非线性动力学特性研究［J］.中国机械工程，2003，14（7）：603-605

The Nonlinear Study on Coupled Bending and Torsion Vibration of Crank Throw

Chen Hongwei，Xiang Jianhua，Liu Shuai，Wu Binhui
School of Mechanical Engineering，Beijing Institute of Technology（Beijing，100081，China）

Based on the simplified model of asymmetric disc rotor and D'alembert's principle，the nonlinear mathematical model of coupled bending and torsion vibration is established，and then the mutual influence between the bending vibration and torsion vibration is studied through the theoretical derivation and the solving methods of iterative numerical of fourth-order Runge-Kutta.The results show that the bending vibration（or torsion vibration）will produce various frequency of torsion vibration（or bending vibration）if coupled.The coupling vibration amplitude will raise with the increasing of the excitation frequency and eccentricity，the bending vibration has a relatively large coupling influence on torsion vibration.

Crank throw，Coupled bending and torsion vibration，Nonlinear vibration，Influence rule

TK422

A

2095-8234（2016）04-0065-06

2016-02-03）

陈宏威（1991-），男，硕士研究生，主要研究方向为内燃机结构振动。

向建华（1976-），男，博士，副教授。