航空发动机吞水试验台喷雾系统数值模拟

米晓童，邢玉明

（北京航空航天大学航空科学与工程学院，北京100191）

航空发动机吞水试验台喷雾系统数值模拟

米晓童，邢玉明

（北京航空航天大学航空科学与工程学院，北京100191）

航空发动机吞水试验中的雨雾环境依靠喷雾系统来实现，喷雾系统能否精确模拟真实大气雨水环境直接关系着试验的可靠性。采用欧拉-拉格朗日粒子追踪方法，对吞水试验台喷雾系统雾化效果的影响因素进行研究。空气相的变化通过求解时均N-S方程得到，离散液滴的变化通过Fluent中的离散相模型进行模拟，液滴的破碎模拟采用Wave模型，碰撞模拟采用O'Rourke模型，传热传质模型采用等温液滴蒸发模型。结果表明：发动机运行状态、喷嘴孔径和喷水量对雾化效果均有影响，但发动机慢车和最大状态时，三者对雾化效果的影响各有不同。

航空发动机；吞水试验；喷雾系统；雾化效果；数值模拟；欧拉-拉格朗日方法

1　引言

飞机在雨雾环境中飞行时，如果发动机吞入大量雨水，会造成机匣局部受冷收缩，致使机匣与叶片之间的间隙减小，从而产生摩擦损坏发动机。此外，也可能使发动机性能恶化，甚至引起压气机喘振、燃烧室熄火。特别是当发动机在慢车状态下工作时，空气流量较小，雨水占空气质量流量的百分比较大，更易引起发动机熄火，引发飞行事故［1］。因此，吞水试验是航空发动机研制必须进行的工作。

航空发动机吞水试验研究的关键，在于通过喷雾系统精确模拟真实大气雨水环境。关于喷雾系统雾化效果研究的数值模拟方法，主要有欧拉-拉格朗日粒子追踪方法和界面追踪方法［2-3］。目前，对航空发动机吞水的研究主要采用试验方法［4-6］，对吞水试验台喷雾系统雾化效果的数值模拟［7-8］主要集中于分析喷嘴布置型式与喷嘴压力对雾化效果的影响，对雾化效果影响因素的研究尚不全面，因此有必要对喷雾系统雾化效果的影响因素进行更为全面研究。

本文采用欧拉-拉格朗日粒子追踪方法，对航空发动机吞水试验台喷雾系统的雾化过程进行模拟，即利用Fluent软件中的DPM模型对吞水试验台喷雾系统进行数值模拟，并在此基础上分析发动机运行状态、喷嘴孔径、喷水量等因素对试验台喷雾系统雾化特性的影响。

2　物理模型与计算方法

2.1物理模型

所研究的航空发动机吞水试验台为直连式结构，其结构如图1所示。

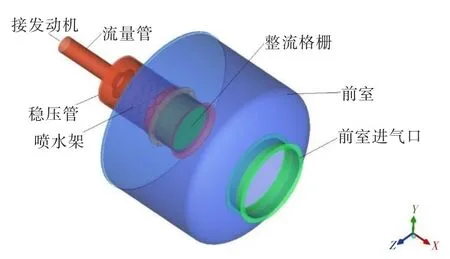
图1　吞水试验台结构示意图Fig.1 The structure of aero-engine water ingestion test bench

由于研究只涉及喷水架至发动机入口截面位置之间部分，故数值模拟区域如图2所示。实际吞水试验过程中，为保证喷嘴喷出的水雾尽可能全部喷射进入流量管，喷嘴位置应靠近流量管——文中喷嘴布置在距离流量管入口收缩段截面50 mm处。采用非结构网格对模型进行划分。由于收缩段对连续相流场的影响较大，而流量管为考察粒径变化的主要区域，因此对这两部分进行网格加密以及边界层设置，如图3所示。网格总数量1 303 569，网格质量0.4以上，满足计算要求。

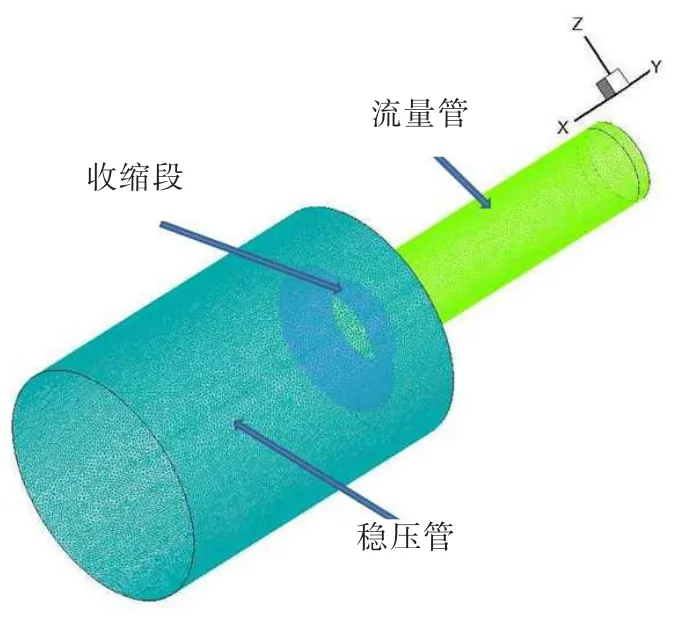
图2　数值模拟计算区域Fig.2 Computational domain of numerical simulation

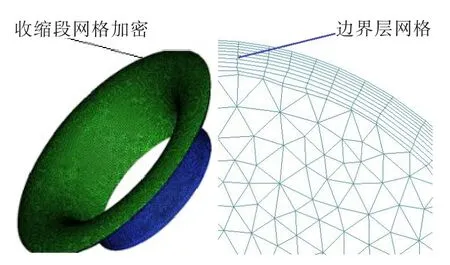
图3　局部网格示意图Fig.3 Local grid schematic diagram

2.2计算方法

空气相运动的控制方程为N-S方程，直接求解对运算设备性能要求过高，因此采用时均化方法对N-S方程进行时间平均处理，补充RNGk-ε湍流模型。在控制方程的离散过程中，选用求解压力耦合方程组的半隐式SIMPLE算法。计算流程如图4所示。

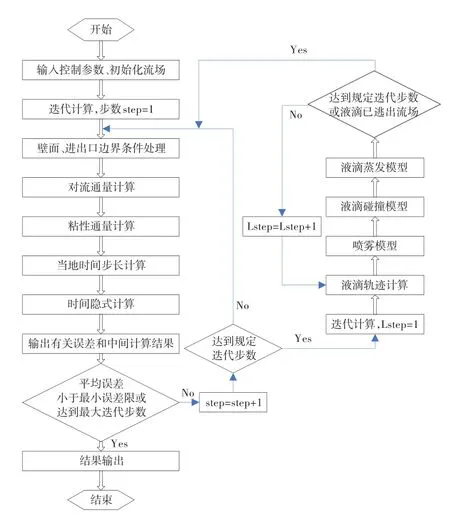
图4　计算流程图Fig.4 Calculation flow diagram

离散液滴破碎模拟采用Wave模型。Wave模型认为，当两种流体存在剪切时，就会产生K-H波，K-H波的不稳定增长将导致液体破碎，新生成的液滴和最快增长的波频率与波长有关；相比于TAB模型，Wave模型对高速环境下的液滴破碎模拟具有更高的精度［9］。碰撞模拟采用O'Rourke模型，传热传质模型采用等温液滴蒸发模型［10］。因吞水试验台喷雾系统中采用直射式喷嘴，喷雾模型选用平口雾化模型。

3　喷雾系统雾化特性影响因素

气流中的液滴破碎受气动力、液体粘性力和表面张力共同影响，气动力促使液滴破碎，表面张力维持液滴稳定，液体粘性力限制湍流发展、阻碍雾化。韦伯数（We）是最重要的控制液滴雾化的参数，在气液物性不发生改变时，We与气液相对速度的平方及特征长度有关。因此，发动机运行状态、喷嘴孔径、喷水量，会对吞水试验台喷雾系统的雾化效果产生影响。

3.1发动机运行状态的影响

发动机运行状态包括最大状态和慢车状态。最大状态空气质量流量为15 kg/s，慢车状态空气质量流量为5 kg/s。空气质量流量变化会对流场中的空气流速造成很大影响，尤其是对流量管中的空气速度。吞水试验台喷雾系统中液滴二次雾化主要发生在流量管中，因此需要对流量管中不同空气速度时喷雾系统的雾化特性进行探讨。本节计算条件为：喷嘴孔径1.50 mm；喷水量0.300 kg/s；空气质量流量1～15 kg/s。

图5为最大状态和慢车状态下计算域的速度云图。可见，收缩段气体速度梯度很大，气体速度在流量管中达到最大值。最大状态下，速度峰值达170 m/s；慢车状态下，速度峰值达60 m/s。

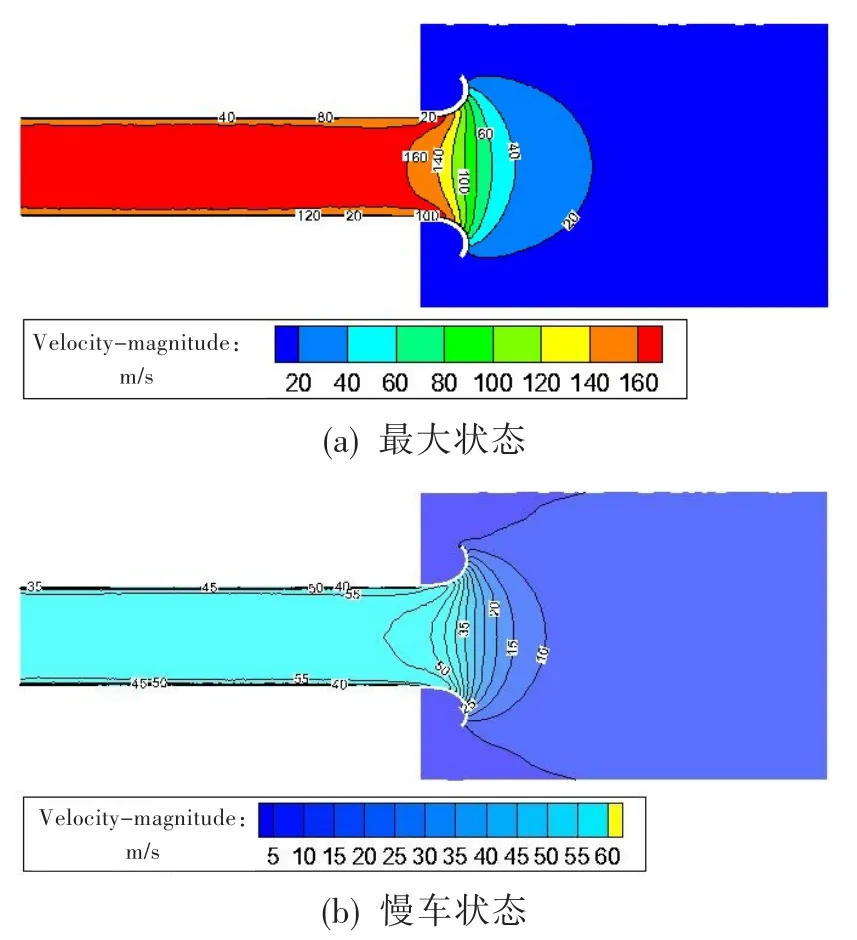
图5最大状态和慢车状态下的速度云图Fig.5 Velocity contours under maximum state and idling state

图6为最大状态下加入液滴颗粒前后连续相流场的速度云图。可见，喷入液滴前，吞水系统的稳压段由于没有水滴影响，流场风速未发生变化；喷入液滴后，在流量管和收缩段中，由于水滴的加入且喷射速度较低（约为60 m/s），与气体产生很大的速度差。气液两相产生强烈的能量交换，使得液滴被加速，喷雾中心区域附近气体被减速，从图中可明显看出中心区域气体速度发生了很大变化。

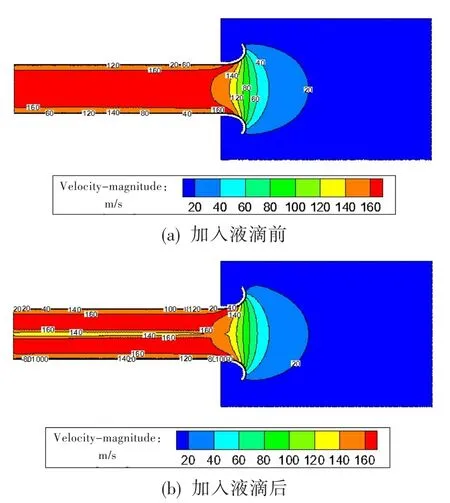
图6　最大状态下加入液滴前后速度云图对比Fig.6 The velocity contour comparison between droplet loaded and unloaded under maximum state

按照前文计算流程，分别对稳压管入口空气质量流量1～15 kg/s进行计算，探讨不同空气质量流量下流量管中液滴粒径的沿程变化。

图7为加入液滴前流量管内空气速度与空气质量流量的关系。可见，流量管内的空气速度与空气质量流量大致成正比关系。对应于1～15 kg/s的质量流量，流量管内空气速度的范围约为11～170 m/s。

图8为加入液滴后流量管入口中心处气液速度差和We与空气质量流量的关系。液滴的初始速度约为60 m/s，气液速度差和We变化范围较大。气液速度差在空气质量流量6 kg/s时达到最小值，约为0.7 m/s；在空气质量流量15 kg/s时达到最大值，约为102 m/s。

图9为不同空气质量流量下流量管内液滴粒径的沿程变化。文中的液滴平均直径为体积平均直径（MVD），液体流动之中定义为。

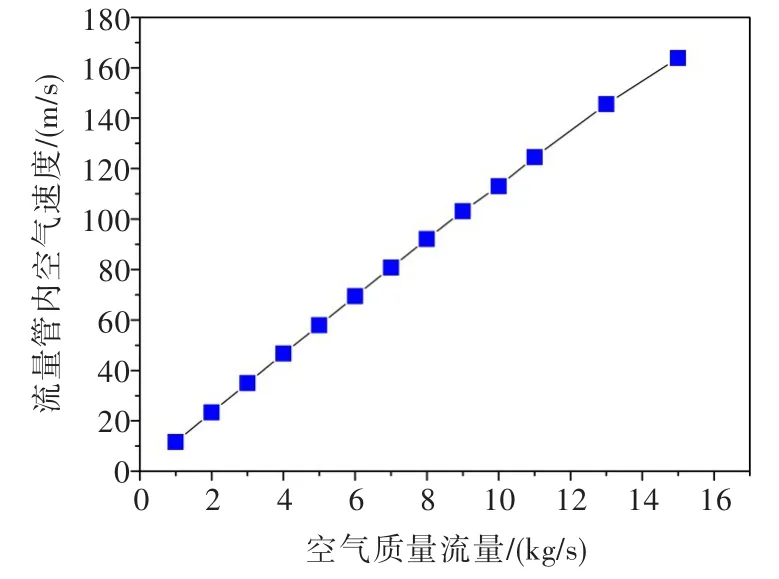
图7　流量管内空气速度与空气质量流量的关系Fig.7 The relationship between air speed and air flow mass rate in flow tube

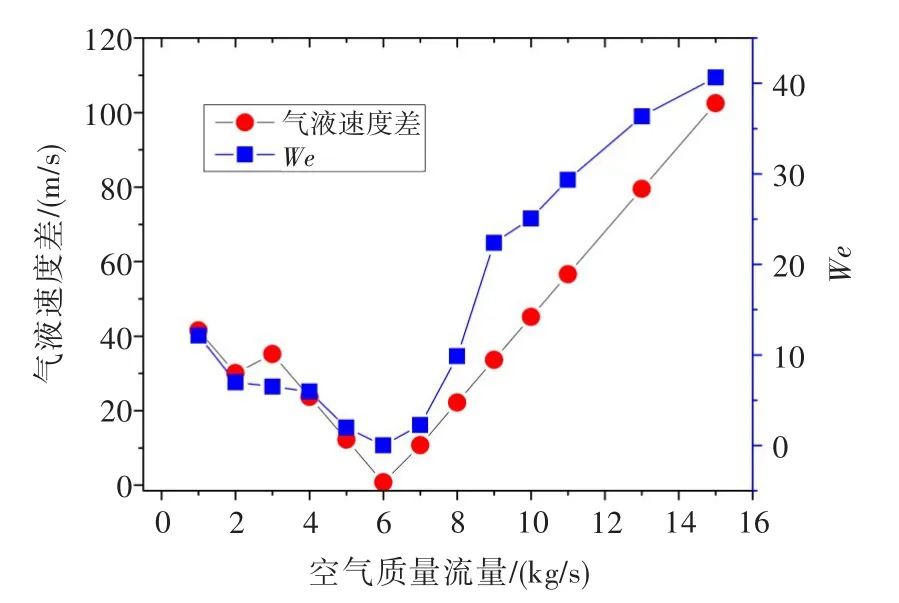
图8　流量管入口处气液速度差和韦伯数与空气质量流量的关系Fig.8 The relationship between air-liquid speed difference/ Weber number and air flow mass rate at the entrance of flow tube

从图9（a）中可看出，空气质量流量1～5 kg/s时，流量管内粒径沿程几乎不发生变化。而由图8可知，质量流量1～5 kg/s时，流量管入口中心处We为2.0～12.0。根据Berthoumieu等［12］的研究，发生气动破碎的必要条件是We＞12.0。由图8还可看出，空气质量流量1～5 kg/s时，流量管内气液速度差随流量的增大而减小。从液滴受力角度分析，位于稳定气流中的液滴受气动力、表面张力和液体粘性力控制。对于低粘度液体，液滴破碎的临界条件即为气动力与表面张力平衡，此时的We为临界韦伯数。We高于临界韦伯数时，液滴发生破碎。因此，气液速度差较大的情况下，液滴的破碎更为充分，最终稳定的液滴直径偏小。这就解释了图9（a）中空气质量流量1～5 kg/s时稳定状态液滴粒径大小的关系。

从图9（b）中可看出，空气质量流量6～8 kg/s时，液滴粒径在流量管中稳定一段距离后呈现出增大的趋势。由图7可知，空气质量流量6～8 kg/s时，流量管入口中心处We＜10.0，故液滴不会发生破碎。另外，由于空气流速增大，在气流作用下液滴发生碰撞而聚合的概率增加，因此液滴粒径会增大。

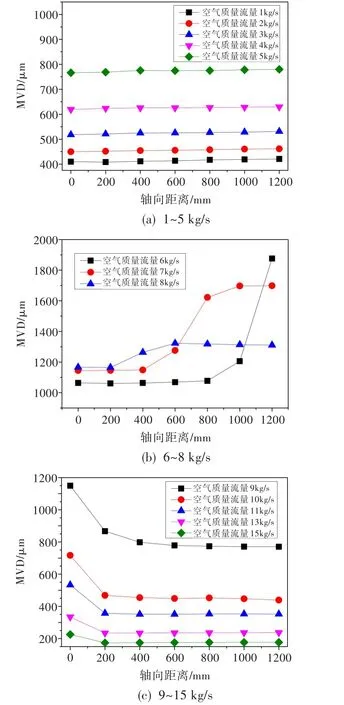
图9　不同空气质量流量下的液滴粒径变化Fig.9 Droplet diameter variation under different air flow mass rate

从图9（c）中可看出，空气质量流量分别为9、10、11、13、15 kg/s时，流量管内粒径沿程减小至稳定。由图8可知，在空气质量流量9、10、11、13、15 kg/s时，流量管入口中心处We＞12.0，满足液滴气动破碎的必要条件，液滴破碎而粒径减小。稳定状态时液滴粒径取决于空气动力和表面张力的关系，空气质量流量较大时，即气液速度差较大时，液滴雾化破碎更加充分，稳定状态液滴粒径更小。

3.2喷嘴孔径的影响

控制喷水量和空气质量流量不变，对比不同孔径时流量管中液滴粒径的沿程变化。计算条件分别为：慢车状态中雨雨量（空气质量流量5 kg/s，喷水量0.25 kg/s），喷嘴孔径d=1.00、1.32、1.33、1.34、1.35 mm；最大状态中雨雨量（空气质量流量15 kg/s，喷水量0.75 kg/s），d=1.50、2.00、2.50、3.00 mm。

图10为慢车状态下喷嘴孔径对液滴粒径的影响。慢车状态下空气流速约为60 m/s，d=1.00 mm时，流量管入口中心处We≈13.0，流量管中液滴粒径基本保持不变；而d=1.35 mm时，流量管入口中心处We≈1.0，液滴能够在更大直径保持稳定，故液滴在碰撞后聚合，粒径增大。从图中可看出，喷嘴孔径的微小变化对雾化效果的影响十分明显。

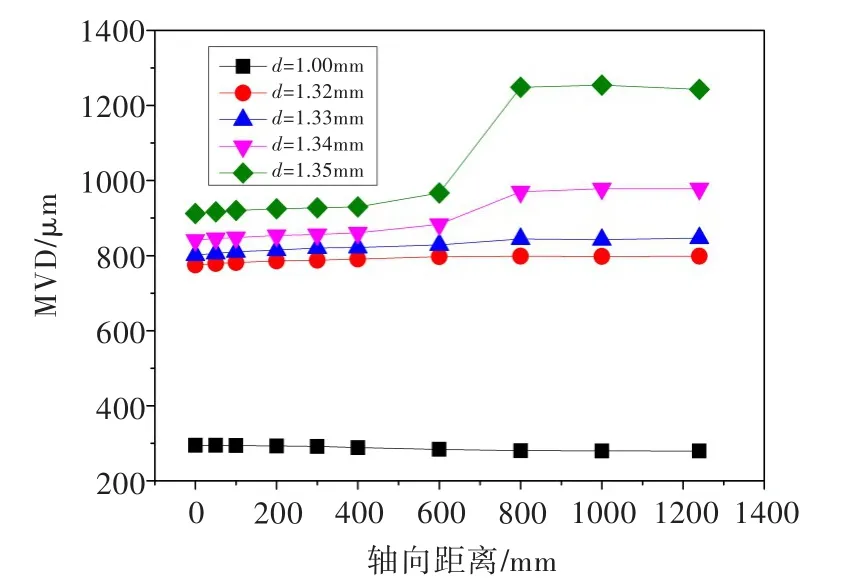
图10慢车状态下喷嘴孔径对液滴粒径的影响Fig.10 The influence of nozzle diameter on droplet diameter under idling state

图11为最大状态下喷嘴孔径对液滴粒径的影响。最大状态下空气流速约为170 m/s，d=1.50 mm时，对应的流量管入口中心处We=5.4，因此液滴不发生破碎，粒径保持稳定；d=2.00、2.50、3.00 mm时，对应的流量管入口中心处We=106.0、188.0、273.0，故液滴破碎，粒径呈现减小的趋势。相同喷水量下，喷嘴孔径较大时液滴速度较低，与空气相对速度较大，根据Hsiang等［13］关于二次雾化的探究可知，液滴颗粒的We越大，破碎相对更加明显。从图中可看出，初始直径相差不大的液滴，最终稳定粒径出现较大差别，说明高速气流中的雾化与静态气流中的差别很大，高速气流对于雾化的影响远比喷嘴本身大。液雾参数取决于二次雾化，为气动力、液体粘性力、表面张力共同作用的结果。

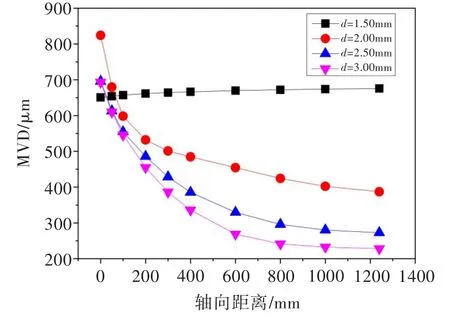
图11　最大状态下喷嘴孔径对液滴粒径的影响Fig.11 The influence of nozzle diameter on droplet diameter under maximum state

3.3喷水量的影响

喷水量直接影响液滴的初始粒径和初始速度。控制喷嘴孔径和空气质量流量不变，对比不同喷水量下流量管中液滴粒径的沿程变化。计算条件为：慢车状态下d=1.50 mm，喷水量m=0.100、0.175、0.250 kg/s；最大状态下d=1.50 mm，m= 0.300、0.525、0.750 kg/s。

图12所示为慢车状态下喷水量对液滴粒径的影响。计算可知，慢车状态下，空气流量5 kg/s、喷水量0.100 kg/s时，流量管入口中心处We=38.0，轴向距离200 mm后液滴粒径基本不再发生变化，说明雾化已基本结束；喷水量为0.175 kg/s和0.250 kg/s时We较小，液滴发生不同程度的聚合，粒径在保持稳定后上升，最终再度稳定。

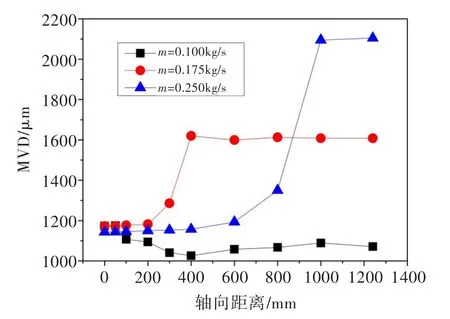
图12慢车状态下喷水量对液滴粒径的影响Fig.12 The influence of water flow rate on droplet diameter under idling state

图13所示为最大状态下喷水量对液滴粒径的影响。最大状态下，空气流速高于水滴喷射初速，喷水量越大气液速度差越小，雾化越不充分。m= 0.300、0.525、0.750 kg/s时，流量管入口中心处We= 342.0、177.0、66.0。m=0.300 kg/s时水滴的MVD最小，且在后半程的喷雾过程中保持不变，说明雾化已基本结束。

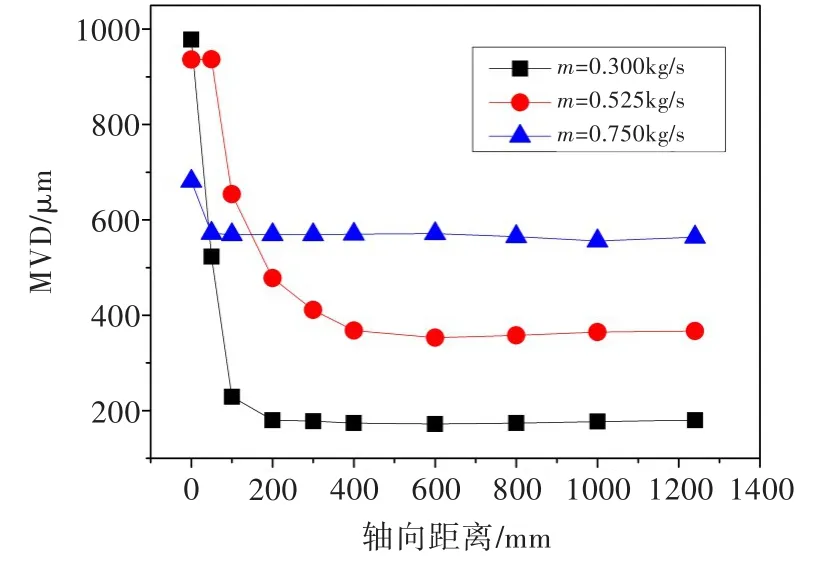
图13　最大状态下喷水量对液滴粒径的影响Fig.13 The influence of water flow rate on droplet diameter under maximum state

4　结论

（1）不同的发动机运行状态下，随着空气质量流量的增加，液滴粒径由沿喷射方向增大逐渐转变为沿喷射方向减小，即液滴由碰撞聚合逐渐转变为破碎，此结果与韦伯数对于液滴破碎影响的理论研究结果一致。

（2）喷嘴孔径对雾化效果影响显著。随着喷嘴孔径的增加，慢车状态下液滴聚合趋势更明显，而最大状态下液滴雾化破碎更显著。高速气流中雾化与静态气流中的差别很大，高速气流对雾化的影响远比喷嘴本身大，液雾参数取决于二次雾化，为气动力、液体粘性力、表面张力共同作用的结果。

（3）喷水量对雾化效果有明显的影响。慢车状态下的结果能通过韦伯数对于液滴破碎的影响给出合理解释；最大状态下，随着喷水量的增加，液滴稳定粒径逐渐增大，雾化破碎越发不充分。

（4）通过对吞水试验台喷雾系统的数值模拟，得出了各因素对雾化效果的影响方式，这对于合理设计喷雾系统、精确模拟真实大气雨水环境具有指导意义。

［1］马庆祥.航空发动机地面模拟吞水试验［J］.燃气涡轮试验与研究，2002，15（4）：39—44.

［2］Tsuji Y，Kawaguchi T，Tanaka T.Discrete particle simulation of two-dimensional fluidized bed［J］.Powder Technology，1993，77（93）：79—87.

［3］Kim D，Desjardins O，Herrmann M.Toward two-phase simulation of the primary breakup of a round liquid jet by a coaxial flow of gas［R］.Center for Turbulence Research，2006.

［4］王月贵，钟华贵，屈成泽，等.小高空台高空模拟试验调试［J］.燃气涡轮试验与研究，2005，18（3）：48—51.

［5］旷桂兰，王道波，单晓明，等.某型航空涡轴发动机整机吞水性能试验［J］.航空动力学报，2009，24（11）：2415—2420.

［6］龚小琦，田小江，吴锋，等.基于试验的高空台混合器至流量管传热模型研究［J］.燃气涡轮试验与研究，2011，24（1）：47—50.

［7］李卫强.高空台吞水试验喷水系统数值仿真研究［D］.北京：北京航空航天大学，2013.

［8］白鹏博，邢玉明，吴峰，等.发动机吞水试验云雾特性数值模拟［J］.航空计算技术，2015，（2）：53—56.

［9］刘昌波，周立新，雷凡培.雾化过程的数值模拟研究综述［J］.火箭推进，2014，（1）：10—17.

［10］胡站伟.结冰风洞云雾参数变化规律初探［D］.四川绵阳：中国空气动力研究与发展中心，2009.

［11］曹建明.喷雾学［M］.北京：机械工业出版社，2005.

［12］Berthoumieu P，Carentz H，Villedieu P，et al.Contribution to droplet breakup analysis［J］.International Journal of Heat&Fluid Flow，1999，20（5）：492—498.

［13］Hsiang L P，Faeth G M.Drop deformation and breakup due to shock wave and steady disturbances［J］.International Journal of Multiphase Flow，1995，24（4）：545—560.

Numerical simulation of spray system in aero-engine water ingestion test stand

MI Xiao-tong，XING Yu-ming
（School of Aeronautic Science and Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

The rain environment in the test is formed by the spray system.Accurate simulation of real atmospheric rain environment is the prerequisite of reliability of the test.Eulerian-Lagrangian particle tracking method was adopted to make numerical simulation research of the spray system atomization effect.Air phase field was calculated by solving time-averaged Navier-Stokes formulation.The droplets were solved by means of discrete phase model in software Fluent.Droplet breakup was simulated by wave model.Droplet collision was simulated by O'Rourke model.Heat and mass transfer was simulated by isothermal droplet evaporation model.The results show that the operating conditions of aero-engine,the diameter of nozzle and the water jet volume have significant influence on the atomization effect.However,the impact varies when engine is in idling or maximum state.

aero-engine；water ingestion；spray system；atomization effect；numerical simulation；Eulerian-Lagrangian method

V241.06；V247.4

A

1672-2620（2016）03-0049-06

2015-08-29；

2015-12-15

航空科学基金（2012024001）

米晓童（1990-），男，河北邯郸人，硕士，研究方向为气液两相流动。