一种改进的多目标粒子群优化算法

何　骞，董轶群，徐文星*

(1.北京化工大学，北京 100029；2.北京石油化工学院，北京 102617)



一种改进的多目标粒子群优化算法

何骞1，董轶群2，徐文星*2

(1.北京化工大学，北京 100029；2.北京石油化工学院，北京 102617)

针对多目标粒子群优化算法在迭代过程中收敛速度和多样性方面的不足，提出一种改进的多目标粒子群优化算法(IMOPSO)。采用基于栅格和拥挤距离的协同外部档案维护策略，通过更准确地选择收敛性和多样性性能更好的非劣粒子作为全局最优值，加快整个种群的收敛速度；采用分段Logistic混沌映射、外部档案检测机制及修改的粒子速度更新公式，分别在初始化阶段和迭代过程中增强种群的多样性；最后，通过对标准测试函数仿真测试证明了改进后的算法能够快速收敛至Pareto最优前沿并保持较好的多样性。

多目标优化；粒子群优化算法；分段Logistic混沌映射；拥挤距离

现实生活中的优化问题因具有较高复杂程度，优化目标往往不唯一。多目标优化问题中不存在唯一最优解，而是综合不同目标函数后所得到的一个最优解集合[1]。因此，在各目标函数之间相互制约的情况下，如何快速、准确地获取多目标问题的最优解集合逐渐成为研究的热点。作为一种新颖的群体智能进化算法，粒子群优化算法(Particle Swarm Optimization，PSO)因模型简单，求解最优解无需梯度信息，对目标函数的复杂程度没有太多要求，易于求解，收敛速度快等特点[2-3]，许多学者对其进行了改进研究。

近年来，Parsopoulos等[4]运用动态权重法将多个目标函数整合为1个目标，利用求解单目标问题的方法求解多目标问题。Mostaghim S等[5]采用ε支配的方式筛选全局最优解，有效地提高了算法的多样性，但是确定ε值存在一定困难。Coello等[6]提出用外部集合保留迭代过程中搜索到的非劣解，改善了算法的效能。Tsai等[7]利用特定的全局最优值来代替个体最优值，充分发挥全局最优值的指导作用。贾树晋等[8]结合增广Lagrange乘子法的方法对种群筛选出爱的非劣解进行局部搜索来逼近Pareto最优解。黄敏等[9]提出自适应的选取全局最优解策略并结合局部搜索来增强种群的搜索能力。王亚辉等[13]提出一种环形链式拓扑结构，将种群划分为多个领域，进行不同的速度位置更新策略。胡旺等[14]提出基于Pareto熵的策略，根据在平行格坐标系统中的分布熵和差熵来衡量种群的性能。虽然尝试了不同的改进方式，但是种群的多样性和收敛速度往往不能兼顾，针对这一问题，笔者对粒子群算法进行了改进，利用标准测试函数来验证算法的性能，在同等条件下与经典MOPSO和NSGA-II以及文献[17]的实验结果对比，结果表明，提出的改进算法能够更好地保持种群多样性的同时提高算法的收敛性。

1　粒子群算法基本原理

人们在研究鸟群觅食行为时发现，鸟类可以通过记忆追踪自己曾经发现过食物的位置以及和整个群体分享个体信息，来协助整个种群快速搜寻到目标物。从而提出粒子群优化算法来解决优化问题[11]。这种借助群体的信息交流与信息共享机制来智能地求解优化问题已经成为新的研究热点。每个粒子代表解空间的一个解，通过参考自身个体的最优位置和全局最优位置不断进行速度和位置的更新，并根据适应度函数来评估每个粒子位置信息的好坏，进行有限次的迭代，使粒子逐渐地逼近优化的目标。

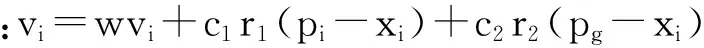
(1)

(2)

其中：r1和r2的取值范围为(0，1)，均服从均匀分布；c1和c2是相应的步长限定因子，通常取[1.2，2.0]区间内的常数，c1的取值决定粒子朝着个体最优方向逼近的步长，c2的取值决定粒子朝着全局最优值方向逼近的步长。式(1)的第1项为动量项，惯性权值w决定对粒子搜寻过程中行进速度的参考权重，采用w由大至小线性递减的策略，可以渐进地加强局部搜索的能力；第2项表示粒子参考自身的历史迭代信息而更新速度的过程；第3项为粒子间信息共享与互动的过程，粒子参考全局最优位置来更新自身速度的过程。

种群粒子能够参考行进过程中个体路过的最优位置和整个种群比较后的最优位置来快速寻找目标，这是粒子群算法的一大优点，同时这种过快的收敛速度也容易破坏整个种群的多样性，笔者在速度更新的时候加入小量扰动，避免整个种群对最优解的依赖性过强，后文详细说明。

随着种群中粒子更新过程的递进，粒子的位置向量可能超过所限制的决策向量边界范围，针对这一问题，将超过边界位置的粒子暂时停留在边界处，同时修改粒子的行进方向，摆脱边界。

2　改进后的粒子群优化算法

针对粒子群算法本身存在的一些缺陷，笔者提出了以下几点改进策略：

(1)采用分段Logistic混沌映射生成初始粒子种群[10]，增强初始粒子种群的随机性，使初始化粒子能够更均匀地分布在决策空间内。

(2)修改种群粒子的更新策略，为了避免种群对粒子的个体性能和社会性能过分依赖而影响粒子的多样性，在迭代过程中加入少量扰动。

(3)把每个粒子的全局最优值的选取和档案维护相结合，将整个种群向Pareto前沿逼近的过程分为2个阶段，分别适应于不同阶段，对非劣解进行维护和筛选优秀的非劣解指导整个种群的收敛。

(4)对外部档案实施实时监测机制，对于当前迭代次数内因为种群无法产生出更好的非劣解，而使得整个种群集中在历史最优解附近甚至收敛至极值点处的问题做出了有效的解决。

2.1初始化粒子群

多目标粒子群(Multi-objective Particle Swarm Optimization，MOPSO)有较强的初值敏感性。传统的MOPSO采用的是在决策变量空间随机生成与种群个数相对应的随机数，确定初始种群时虽然具备一定的随机性，但是初始种群的分布较为散乱。为了使初始种群尽可能均匀地分布在全部决策空间内，在不失初始种群粒子的随机性上增加初始种群的分布性能，引入分段Logistic混沌映射在种群初始值的确定中[10]。

混沌映射的数学达式为：

(3)

其中，3.569 945 6…≤μ≤4，a0∈(0，1)。

a0在(0，1)范围内取值，服从均匀分布，根据a0的数值大小结合式(1)给出的范围，选择一种计算方式进行计算，重复操作每1个粒子，直至达到种群数量的要求。

2.2全局最优值的选取

迭代过程中粒子全局最优值的选取和对外部存储非劣解的档案维护是MOPSO算法设计的2个重要部分。外部档案的维护有2个关键点：第1是如何从外部档案中筛选收敛性和多样性表现较好的非劣解作为全局最优值指导粒子朝更好的方向搜索，关键是对粒子的性能评判；第2是存储非劣解的外部档案如果超过预先设置的大小后，如何剔除收敛性和多样性相对不好的非劣解。笔者利用栅格法和拥挤距离相互协调的方式共同调整外部档案的非劣粒子的排列方式，从而选取相对性能更好的非劣粒子作为指导粒子。

在整个种群迭代过程的前期，外部档案集里面存储的非劣粒子相对较少，如何从稀疏的集合中筛选出收敛性和多样性表现更好的粒子作为全局最优解来指导种群收敛成为关键。假设待优化的目标有2个，分别记为f1和f2，则迭代过程前期外部档案粒子分布状况如图1所示。

如果令C来存储外部非劣解档案中多样性和收敛性能较好的粒子作为选取全局最优值的候选集合，其中x4，x5，x6，x74个粒子多样性表现较好，而对于前3个粒子来讲，多样性能差不多，x3距离原点最近，收敛性能更好，则候选集合C=[x3，x4，x5，x6，x7]。

采用网格法进行分类，粒子x2，x3在同1个网格里，根据轮盘赌方式从该网格中选择1个粒子，假设选择的是x3，最终外部档案NP中表现出多样性较好的粒子候选集合C表现为：C=[x1，x3，x4，x5，x6，x7]，但是网格法操作起来有2个弊端：一是算法复杂度较高，运算速度较慢；二是在算法的前期，数值收敛性能判断不出来，依靠轮盘赌选择的粒子具有一定的随机性。同时由图1可知，如果粒子数目较多，因为网格的关系，一些表现不好的非劣粒子因为独自占有1个网格，同样会被选取，而影响这个种群的收敛特性，并且粒子较多的时候就不能完全选择出如上所示的粒子了。

常用的拥挤距离精英策略同样存在一定的弊端，如图1所示，粒子x5相邻的2个粒子x4，x6，以x4，x6为2个对角顶点构成正方形，则该正方形对角线长度即为x5的拥挤距离值。那么根据拥挤距离降序排列则是[x1，x7，x6，x4，x5，x3，x2]，一般将边界解设置为Inf，精英法则选取外部档案大小的20%的粒子作为指导粒子，最终候选集合C=[x1，x7]，在迭代过程前期，外部档案中粒子较少的情况下，传统的采用基于精英拥挤距离策略来筛选全局最优粒子显然缺失多样性。

在算法迭代初期，外部档案存储的粒子数目较少时，利用栅格法将粒子所在空间的一侧均匀分成k个栅格，分割的目的和网格法相似，但是算法运算复杂度会小很多，目的是将目标函数所在区域空间均等划分，如图2所示。粒子x1，x2，x3在同一个栅格内，多样性指导方面，3个粒子的指导性相近，但是在收敛性方面，x3距离坐标原点最近，收敛性能表现最强，所以选择x3，其他粒子依次选择为C=[x3，x4，x5，x6，x7]。这种方法设计简单，在粒子寻优迭代前期，能够以最快的速度筛选出最合适作为全局最优值候选解的集合。

当档案中非劣粒子的数目达到数值K时，再使用上述筛选策略就存在一定的局限性，因为在未知目标问题的前提下，1个栅格内距离原点最近的粒子不一定足够代表该粒子具有更好的收敛性能，当1个栅格内同时存在过多粒子时，选取方面就会产生较大障碍。因此使用拥挤距离评估法。由图2可知，定义边界粒子x1，x7的拥挤距离为这2个粒子分别到与他们各自相邻那个粒子之间的欧氏距离，非边界粒子的定义方式，如x5的拥挤距离定义方式，取x5分别到x4和x6的欧氏距离d54和d56，用d5代表x5的拥挤距离，则数学表达式为d5=(d54+d56)/2。这种定义方式运算简便，并且能够直观准确地表示1个粒子对于相邻2个粒子的拥挤程度。边界粒子的拥挤距离取Inf，会导致在根据拥挤距离排序时边界粒子始终会被选择成为指导粒子，并且在好几代种群中都无法被替换掉，该定义方式能够有效避免这一恶性循环。

2.3外部档案维护

整个种群如果过分依赖全局最优值，很快会收敛至全局最优值附近，如果全局最优值不能完全代表整个种群的多样性性能，则这种过快收敛就会在一定程度上破坏种群的多样性。笔者提出一种将外部档案中未被选择成为全局最优值的粒子作为小量扰动，加入到速度更新公式中，则速度更新公式为：

vi=wvi+c1r1(pi-xi)+c2r2(pg-xi)+

(4)

其中，c3r3(pd-xi)即是扰动项，扰动项太大，则会影响粒子的收敛，因此扰动因子c3数值较小，定义范围和c1，c2一样。r3的取值在区间(0，1)范围内，并服从均匀分布。pd表示该项的扰动粒子，外部档案中的非劣解没有被选成全局最优值的粒子，利用轮盘赌的方式选择1个作为扰动粒子，以避免整个种群对历史最优解的过分依赖而导致的集群收敛。

随着迭代过程的推进，群体中产生的非劣解的数量也越来越多，外部档案中存储的非劣解的数量基数太大，收敛性能和多样性性能表现相差无几的粒子无法被淘汰掉，档案中粒子冗余严重，因此需要对外部档案进行维护。笔者基于拥挤距离参数逐个淘汰机制来剔除档案中表现不好的非劣解，以保证档案中非劣解的质量，如图3所示。

由图3(a)可知，假设当前外部档案中有7个粒子，如果外部档案最大能容纳粒子数为4，那么就需要剔除多余的粒子。如果档案中按照拥挤距离排序，将拥挤距离数值排在末尾的粒子剔除掉，则维护完档案后如图3(b)所示，如果采用基于拥挤距离逐个淘汰机制来维护档案，首先剔除拥挤距离值最小的x4，接着重新计算当前档案中各粒子的拥挤距离值，并排序后剔除排在末尾的粒子x2，重复上述操作，直至档案大小满足要求。最终结果如图3(c)所示。从图3可以清晰地看出，基于拥挤距离逐个淘汰机制的作用。

针对粒子陷入极值的状况，笔者提出一种监测选择机制，具体过程如下：

Step1设NP为外部档案，令NP的极限大小为nmax，当前NP的大小为M，P为粒子群体。初始化外部档案，比较初始粒子群中各个粒子的非劣关系，将非劣解存入外部档案NP中；

Step2每次迭代更新NP过程中，取xi∈P，(i=1，…，N)，其中N为种群大小，比较xi与xj∈NP(j=1，…，M)的非劣关系，如果xi≻xj，则xi加入NP，相应的xj从NP中剔除；如果xj≻xi，则i=i+1；如果两者无支配关系，也将xi存入NP中。比较粒子支配关系过程中，目标函数值相等的情况也将被加入外部档案中，也就是说，档案里面允许相等的值同时存在；

Step3在更新档案后，如果档案中出现重复粒子，则判断种群有陷入局部极值的可能性，设置陷入局部极值标志位为1，否则为0。同时如果判断有陷入局部极值的可能性，则在粒子更新位置和速度时导入第2套速度更新方案。即保留当前种群70%的粒子，为保证公平性，这些粒子是随机选择的，同时再产生30%的新粒子混合进入种群，增加种群的多样性，从而在目标空间产生更多的位置来辅助跳出局部极值。如果陷入局部极值标志位为0，则正常更新粒子位置和速度；

Step4如果M>nmax，则采用基于拥挤距离逐个淘汰机制修剪档案的大小，剔除表现不好的非劣解，确保档案的有限性。

2.4IMOPSO算法流程

采用基于栅格和拥挤距离的协同外部档案维护策略加速收敛，采用分段Logistic混沌映射、外部档案监测选择机制及修改的粒子速度更新公式增强多样性，得到的IMOPSO算法完整步骤如下：

Step1初始化算法的基本参数信息，使用分段Logistic混沌映射方法初始化粒子种群；

Step2计算种群的初始位置，以粒子当前的位置作为个体初始最优值，比较粒子之间的非劣关系，确定初始外部档案NP，利用栅格法在NP中筛选每个粒子的初始全局最优值gbest；

Step3判断粒子陷入局部极值标志位，如果为0，则通过式(4)更新粒子当前的速度，通过式(2)更新粒子当前的位置，判断速度、位置信息是否超出所限制的边界，做边界限制，如果局部极值标志位为1，则保留原先种群70%的原始粒子，导入30%的新粒子混合进种群协同搜索；

Step4比较新一代粒子的位置信息，确定个体最优值，如果新粒子的位置信息非劣于原个体最优位置信息，则替换原个体最优位置，否则不替换；

Step5比较新一代粒子和档案中粒子的非劣性，添加更好的非劣粒子进入档案，同时剔除档案中被支配的粒子。判断外部档案中当前粒子数M是否小于K，如果是，则采用栅格法在外部档案中筛选全局最优值，如果否，则采用拥挤距离策略筛选全局最优值，通过轮盘赌的方式选择未成为全局最优值的粒子成为扰动量pd；

Step6基于拥挤距离逐个淘汰和监测选择机制维护外部档案；

Step7判断迭代次数是否满足终止条件，如果满足终止条件则算法结束，不满足终止条件则跳转Step3，继续搜寻。

3　性能测试

为了验证改进后算法的性能，利用经典测试函数ZDT-1、ZDT-2和ZDT-3进行仿真实验[15]，并与文献[17]所提出算法的实验结果进行比较。为了方便与文献[17]中的算法做比较，令文献[17]中的算法名称为X，改进算法定义为IMOPSO，目标函数评价次数为25 000次，算法运行30次。

3.1性能指标

(1)世代距离(GD)是描述算法运算求解得到的非劣解与目标问题的真实Pareto前沿之间距离的参数，数学表达式为[16]：

(5)

式中，di表示相应的第i个粒子与真实Pareto前沿的最短距离。

(2)分布均匀度量(SP)是评价算法求解得到的Pareto最优解集中分布性能好坏的一个参数。其数学表达式为：

(6)

3.2实验结果及分析

不同算法的GD和SP数值在3个测试函数上面的性能表现如表1所示，不同算法针对不同的测试函数的运行时间如表2所示，改进后粒子群算法针对3个测试函数的测试结果如图4～图6所示。

由表2可以看出，提出的改进算法IMOPSO在运行时间上与其他3种算法相比，收敛速度明显加快，能够以更快的速度逼近最优Pareto前沿。分析表1中记录的SP统计参数可以看出，对于ZDT-1和ZDT-2，IMOPSO的表现更好，ZDT-3则和文献[17]提出的算法

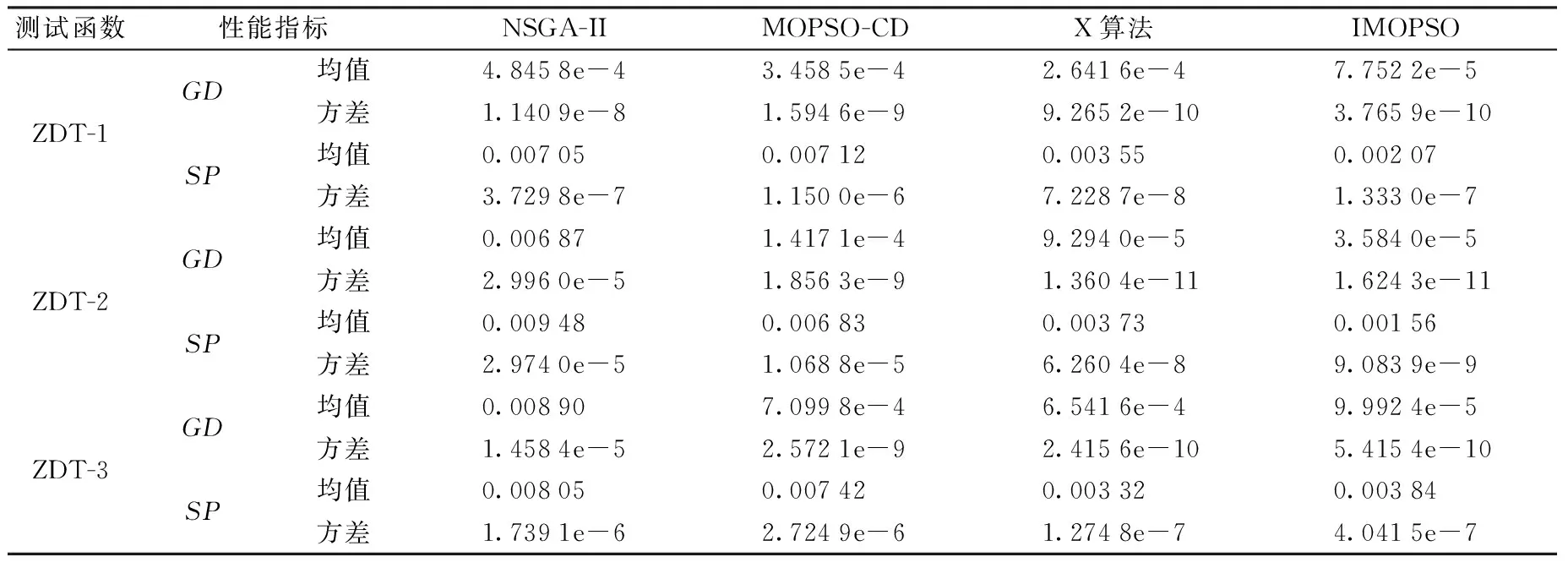
表1　4种算法对比测试结果

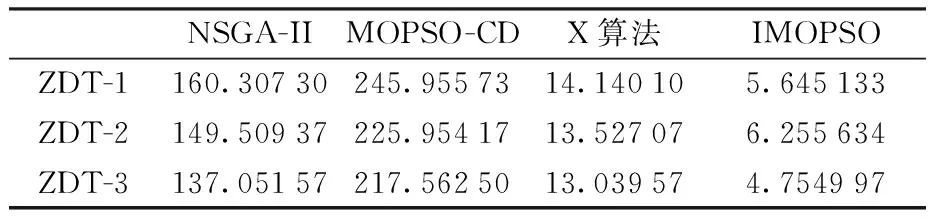
表2　平均运行时间　s

相差无几，比传统的MOPSO和NSGA-II有较大的变化，多样性性能表现更好。分析GD指标的均值和方差可以看出，在方差值相差不大，也就是稳定性能表现良好的前提下，GD的数值IMOPSO要比文献[17]提出的算法高1个数量级，比MOPSO和NSGA-II高1～2个数量级，证明IMOPSO的收敛性能表现更好。

4　结论

通过引入Logistic混沌映射初始化种群，改进了基于非劣分类和密度距离淘汰机制，对外部档案中的粒子进行预判断，有效避免了粒子陷入极值的状况。根据外部档案里的非劣粒子数量提出不同状态下选取全局最优值的方法，加快了种群的收敛速度。同时将档案中未被选择成为全局最优解的粒子筛选出来成为扰动项并加入粒子更新过程中，避免了种群对全局最优解和个体最优解的过分依赖而丧失多样性。通过benchmark的仿真测试，证实了笔者提出的IMOPSO算法，在稳定性、收敛速度和多样性方面表现优异。

[1]Steuer R E. Multiple criteria Optimization: Theory， Computation and Application[M]. New York: Wiley， 1986

[2]Kennedy J， Eberhart R. Particle swarm optimization[C]. IEEE International Conference on Neural Networks， 1995. Proceedings. 1995,4:1942-1948.

[3]Eberhart R， Kennedy J. A new optimizer using particle swarm theory[C]. International Symposium on MICRO Machine and Human Science, 1995:39-43.

[4]Parsopoulos K E， Vrahatis M N. Particle swarm optimization method in multiobjective problems[C]. ACM Symposium on Applied Computing, 2002:603-607.

[5]Mostaghim S， T eich J. The role ofε-dominance in multi-objective particle swarm optimization method[C]. Proc of the 2003 Congress on Evolutionary Computation. Canberra: IEEE， 2003:1764-1771.

[6]Coello C C A， Pulido G T， Lechunga M S. Handling multiple objectives with particle swarm optimization[J]. IEEE Trans on Evolutionary Computation， 2004，8(3):256-279.

[7]Tsai S J， Sun T Y， Liu C C， et al. An improved multi-objective particle swarm optimizer for multi-objective problems[J]. Expert Systems with Applications， 2010，37(8):5872-5886.

[8]贾树晋，杜斌，岳恒.基于局部搜索与混合多样性策略的多目标粒子群算法[J].控制与决策，2012(6):813-818，826.

[9]黄敏，江渝，毛安，等.基于全局最优位置自适应选取与局部搜索的多目标粒子群优化算法[J].计算机应用，2014(4)：1074-1079.

[10]范九伦，张雪锋.分段Logistic混沌映射及其性能分析[J].电子学报，2009(4)：720-725.

[11]Kennedy J. The Particle Swarm: Social Adaptation of Knowledge[C]. Proceedings of IEEE International Conference on Evolutionary Computation， Indianapolis， Indiana， 1997.

[12]雷德明，吴智铭.Pareto档案多目标粒子群优化[J].模式识别与人工智能，2006(4)：475-480.

[13]王亚辉，唐明奇. 多邻域链式结构的多目标粒子群优化算法[J]. 农业机械学报，2015(1)：365-372，358.

[14]胡旺，Gary G. YEN，张鑫.基于Pareto熵的多目标粒子群优化算法[J].软件学报，2014(5)：1025-1050.

[15]Zitzler E， Deb K， Thiele L. Comparison of multiobjective evolutionary algorithms: empirical results[J]. Evolutionary Computation， 2000，8(2):173-195.

[16]Veldhuizen D A V， Lamont G B. Evolutionary computation and convergence to a pareto front[C]. Stanford University California， 1999:221-228.

[17]陶新民，徐鹏，刘福荣，等.一种组合粒子群和差分进化的多目标优化算法[J].计算机仿真，2013(4)：313-316.

An Improved Multi-Objective Particle Swarm Optimization Algorithm

HE Qian1, DONG Yi-qun2, XU Wen-xing*2

(1.Beijing University of Chemical Technology， Beijing 100029， China;2.Beijing Institute of Petrochemical Technology， Beijing 102617， China)

An improved multi-objective particle swarm optimization algorithm is proposed to improve the convergence speed and diversity in the iterative process of multi objective particle swarm optimization algorithm. Based on grid and crowding distance collaborative external archive maintenance strategies, the algorithm utilizes the non-inferior particles which have more accurate selection of convergence and diversity of better performance as the global optimum value, to accelerate the speed of convergence of the whole population. By using the piecewise Logistic chaotic map, the external file detection mechanism and the modified particle velocity updating formula, the diversity of the population is enhanced during the initialization phase and the iteration process. Finally, the improved algorithm can quickly converge to the Pareto optimal front and maintain a good diversity by the simulation test of the standard test function.

multi objective optimization; particle swarm optimization algorithm; piecewise logistic chaotic map; crowding distance

2016-03-16

国家自然科学基金项目(61304217)；北京市教委科技项目(KM20150017003)。

何骞(1990—)，男，硕士研究生，研究方向为多目标粒子群优化算法，E-mail:heqian916@163.com。

TP18

A