相对密实度对砾砂初始切线模量的影响*

陈　晨

(1. 东北大学 资源与土木工程学院， 沈阳 110819； 2. 中国建筑东北设计研究院有限公司 基础设施事业部， 沈阳 110003)



相对密实度对砾砂初始切线模量的影响*

陈晨1，2

(1. 东北大学 资源与土木工程学院， 沈阳 110819； 2. 中国建筑东北设计研究院有限公司 基础设施事业部， 沈阳 110003)

针对基坑施工过程中周边土体由于受到扰动而发生结构性变化，致使土体强度和变形特性改变这一问题，选取典型砾砂进行不同围压下的三轴固结排水剪切试验，得到砾砂Duncan-Chang模型的相关参数.探讨了砾砂的初始切线模量Ei对相对密实度Dr的影响规律，并应用数学手段对与Ei有关的无量纲参数K和Dr的关系进行拟合.结果表明，相对密实度Dr对砾砂的强度和变形特性有着重要影响，lnK与Dr大致呈二次函数关系.

砾砂； 三轴试验； 相对密实度；Duncan-Chang模型； 扰动状态； 初始切线模量； 强度和变形特性； 对数拟合

沈阳位于浑河由山区流向平原出口的新老冲洪积扇上，地层主要由第四系堆积物所组成.自地表下依次为杂填土、黏性土、砾砂、圆砾及卵石[1].其中，杂填土层与黏性土层的厚度较小，约为0.5～3.0m，卵石层的埋深较深，对工程影响相对较小[2]，而砾砂是沈阳地区广泛分布的主要地基土，因此，极有必要对沈阳地区砾砂的变形及强度特性进行深入研究，使其能更好地描述沈阳地区砾砂的力学性状与行为.

基坑施工过程中，伴随着开挖和回填，基坑周边土体受到扰动，土体的结构性也发生变化.Desai提出了扰动状态概念(DSC)理论[3-5]，他认为扰动引起的土体改变可以用密度ρ、含水量ω、不均匀系数Cc或曲率系数Cu、相对密实度Dr和孔隙比e等土性参数的改变来描述.而在土体扰动过程中，相对密实度Dr的变化较其他参数变化尤为明显[6-7].因此，有必要研究和探讨相对密实度Dr对现有土体本构模型中参数的影响规律.

本文首先对砾砂的固结排水三轴试验结果进行详实的归纳与分析，计算得到砾砂Duncan-Chang模型的相关参数.随后探讨了沈阳地区砾砂的初始切线模量Ei受相对密实度Dr的影响规律，并应用数学手段对Dr与Ei的关系进行拟合，为今后沈阳地区的岩土工程问题服务.

1　砾砂三轴压缩试验方案

在沈阳地区取砾砂原状样，其颗粒级配曲线如图1所示，颗粒粒径主要集中在2～10mm之间.为了保证重塑样均匀且更接近原状样，砾砂基本物理参数如表1所示.

本文采用南京泰克奥科技有限公司生产的LH-TTS-SSeries型全自动应力路径三轴仪进行固结排水剪切试验(CD试验).试验仪器和砾砂试样如图2所示.根据土体相对密实度的不同，分为4种工况进行试验，即Dr分别为0.5、0.6、0.7和0.8，试样直径为150mm，高为300mm，制样时分7层填筑，各工况下的试样总质量和每层质量可根据相应Dr换算得出，制样干密度ρd、试样总质量m及每层填筑质量ms如表2所示.每种工况的试样分别在100、150、200、250和400kPa围压下进行试验，共有60组.剪切试验时，试样需首先通过反压进行饱和(反压力为220kPa，B不小于0.95，B为表征土体饱和度的土体孔隙压力系数，对于饱和土体，B值为1).综合效率和精度两方面考虑，采用0.015mm/min的剪切应变速率进行固结排水试验，试验破坏标准均按照峰值强度确定.

图1　沈阳砾砂颗粒级配曲线Fig.1　Grading curve for gravelly sand in Shenyang

表1　基本物理参数

图2　试验仪器及砾砂试样Fig.2　Test instruments and sample of gravelly sand表2　砾砂试验条件Tab.2　Test conditions for gravelly sand

工况ρd/(g·cm-3)m/gms/g11.648694124221.598428120431.558218117441.5079521136

2　砾砂的变形和强度特性

2.1应力-应变关系曲线

4种围压条件下，4种不同相对密实度的沈阳地区砾砂重塑样(Dr=0.5，0.6，0.7，0.8)的三轴剪切试验结果如图3所示.由图3可知，砾砂的应力-应变曲线呈现如下规律：

1) 在相同相对密实度Dr条件下，砾砂的峰值强度会随着围压σ3的增大而逐渐增大；随着砾砂相对密实度Dr的增加，其峰值强度(σ1-σ3)f也会相应增大.

2) 弹性阶段内，相同的围压条件下，砾砂的偏应力(σ1-σ3)-轴向应变ε1曲线的斜率会随相对密实度Dr的增大而逐渐增大，这说明初始状态下的砾砂越密实，其初始切线模量Ei越大.

图3　不同围压下砾砂应力-应变关系曲线Fig.3　Stress-stain relationship curves for gravellysand under different confining pressures

3) 当砾砂试样出现峰值强度时，其轴向应变ε1的变化范围在7%～11%之间.

4) 随着围压σ3的增大，砾砂试样出现峰值强度(σ1-σ3)f时所对应的轴向应变ε1也随之增大.

2.2砾砂密实度对初始模量的影响

由图3可知，偏应力(σ1-σ3)-轴向应变ε1关系曲线与Kondner[8]提出的土体双曲线型应力-应变关系相似.故本文用双曲线近似拟合出砾砂的应力-应变关系曲线，双曲线方程和初始切线模量Ei的表达式分别为

(1)

(2)

式中：b为双曲线的渐近线所对应的极限偏差应力(σ1-σ3)ult的倒数；a为初始切线模量Ei的倒数.

本文采用邓肯等人在1970年提出的方法[9]，采用经验公式求解计算参数a.由于篇幅所限，此处不再赘述.

Janbu[10]发现土体的初始切线模量Ei与第三主应力(侧限压力)呈指数函数关系，其表达式为

(3)

式中：K、n为试验参数；pa为标准大气压力.

绘制出lg(Ei/pa)与lg(σ3/pa)的关系曲线，二者大致呈线性关系.不同相对密实度下lg(Ei/pa)与lg(σ3/pa)的关系曲线如图4所示.

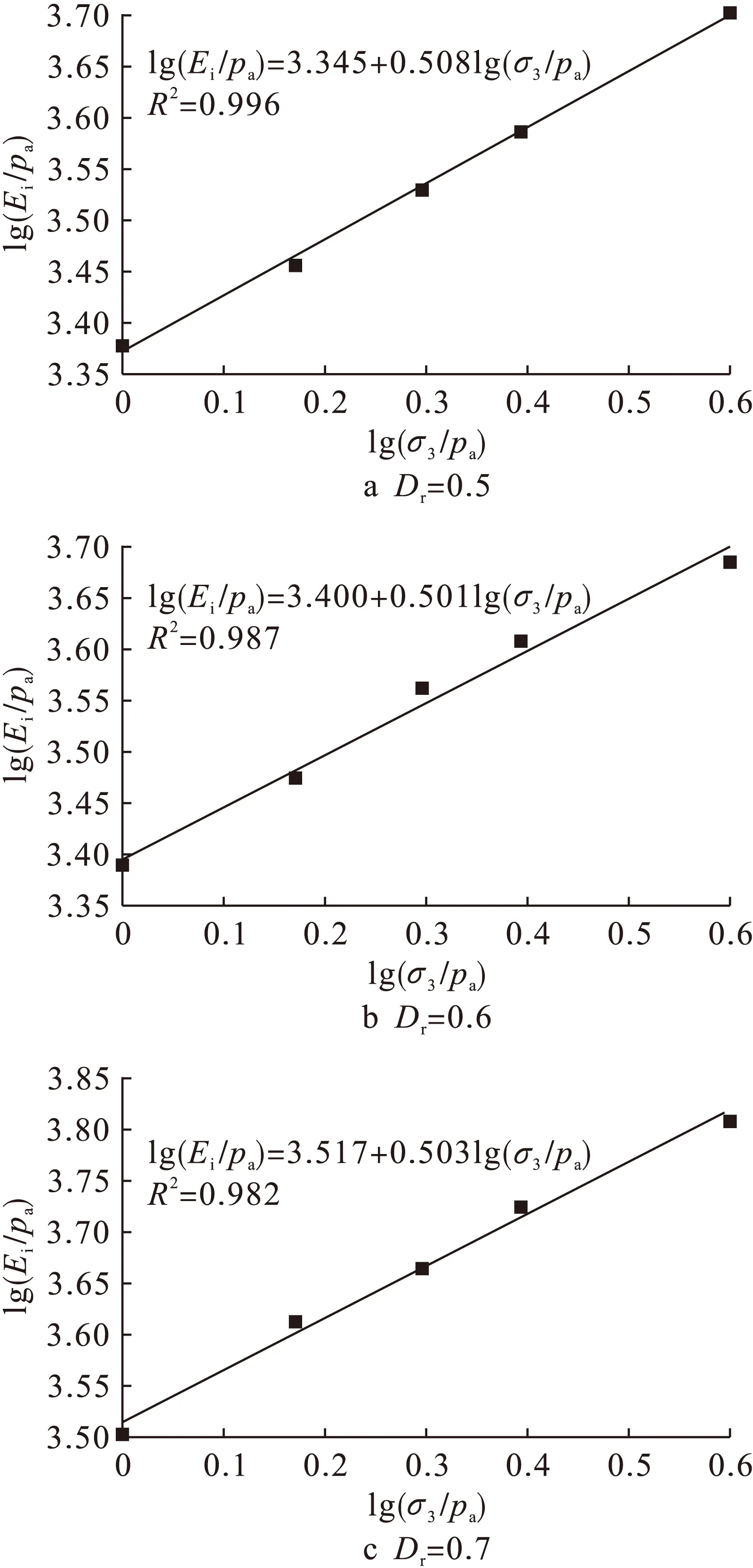
图4　不同相对密实度下lg(Ei/pa)与lg(σ3/pa)的关系曲线Fig.4　Relationship curve between lg(Ei/pa) andlg(σ3/pa) under different relative densities

计算得到的K和n如表3所示.由表3可知，参数n在不同相对密实度条件下保持稳定，不随密实度的变化而大幅度变化，说明Dr对试验参数n的影响甚微，可近似认为参数n不受扰动的影响.然而，随着相对密实度Dr的增大，试验参数K呈现显著增长的趋势，对比Dr=0.5和Dr=0.8两种工况，K值增加了约一倍，这说明试验参数K受扰动影响十分明显.

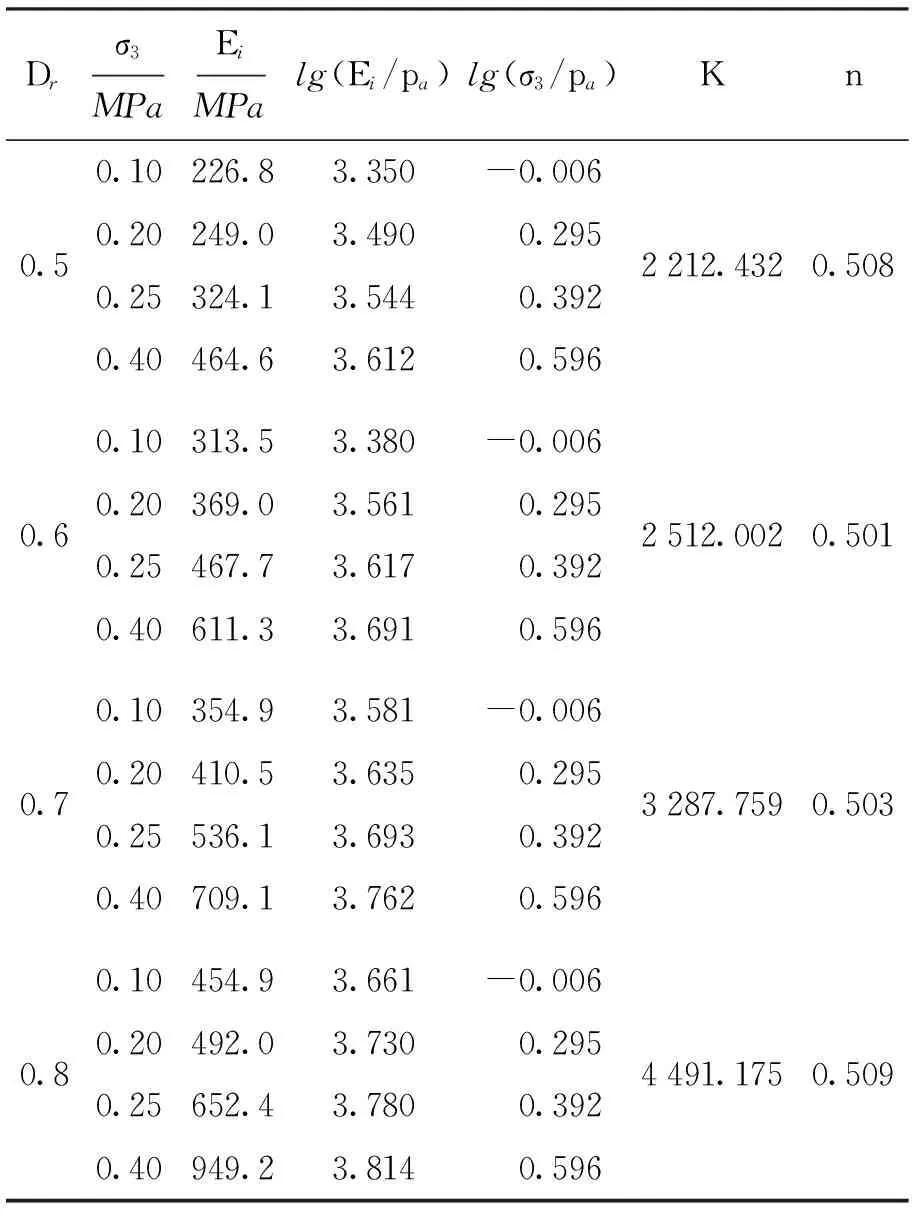
表3　砾砂在不同相对密实度下的K和n值

对K和Dr进行拟合，即

(4)

式中，e、c、d为无量纲参数.拟合数据如图5所示.由图5可知，lnK与相对密实度Dr之间大致呈二次函数关系，曲线相关系数R2=0.995，拟合程度良好.对于沈阳地区的砾砂，试验得到的无量纲参数e的取值约为7.60；无量纲参数c的取值约为-1.27，无量纲参数d的取值约为2.83.

图5　砾砂试样的ln K-Dr关系曲线Fig.5　Relationship curve between ln K andDr for sample of gravelly sand

3　结　论

相对密实度Dr对砾砂的初始切线模量有重要影响.本文经过分析，得出如下结论：

1) 随着砾砂相对密实度Dr的增加，其峰值强度(σ1-σ3)f也会相应增大.在弹性阶段内，相同的围压条件下，砾砂的偏应力(σ1-σ3)-轴向应变ε1曲线的斜率会随相对密实度Dr的增大而逐渐增大，这说明初始状态下的砾砂越密实，其初始切线模量Ei越大.

2) 参数n在不同相对密实度下保持稳定，不随密实度的变化而大幅度变化，Dr对n的影响甚微，可以近似认为n不受扰动的影响.然而，随着相对密实度Dr的增大，参数K呈现显著增长趋势，参数K受扰动影响十分明显.

3)lnK与相对密实度Dr之间大致呈二次函数关系，对于沈阳地区的砾砂，试验得到的无量纲参数e的取值约为7.60；无量纲参数c的取值约为-1.27，无量纲参数d的取值约为2.83.

[1]王鑫，张庆贺，陈宇，等.城市过街地道施工阶段数值模拟分析 [J].地下空间与工程学报，2011，7(3)：534-540.

(WANGXin，ZHANGQing-he，CHENYu，etal.Numericalanalysisonconstructionofcitypedestrianunderpass[J].ChineseJournalofUndergroundSpaceandEngineering，2011，7(3)：534-540.)

[2]万波，石彦文，赵连升，等.沈阳市城区第四纪地层的划分 [J].东北地震研究，2001，17(2)：41-47.

(WANBo，SHIYan-wen，ZHAOLian-sheng，etal.DivisionofquaternarylayersinShenyangurbanarea[J].SeismologicalResearchofNortheastChina，2001，17(2)：41-47.)

[3]DesaiCS.Aconsistentfiniteelementtechniqueforworksofteningbehavior[C]//ProceedingofInternationalConferenceonComputerMethodsinNonlinearMechanics.Austin，USA，1974：969-978.

[4]ParkIJ，DesaiCS.Cyclicbehaviorandliquefactionofsandusingdisturbedstateconcept[J].JournalofGeotechnicalandGeoenvironmentalEngineering，2000，126(9)：834-846.

[5]PadhanSK，DesaiCS.DSCmodelforsoilinterfaceincludingliquefactionandpredictionofcentrifugetest[J].JournalofGeotechnicalandGeoenvironmentalEngineering，2006，132(2)：214-222.

[6]朱剑锋，徐日庆，王兴陈，等.考虑扰动影响的砂土弹塑性模型 [J].岩石力学与工程学报，2011，30(1)：193-201.

(ZHUJian-feng，XURi-qing，WANGXing-chen，etal.Anelastoplasticmodelforsandconsideringdisturbance[J].ChineseJournalofRockMechanicsandEngineering，2011，30(1)：193-201.)

[7]徐日庆，张俊，朱剑锋，等.考虑扰动影响的修正Duncan-Chang模型 [J].浙江大学学报(工学版)，2012，46(1)：1-7.

(XURi-qing，ZHANGJun，ZHUJian-feng，etal.ModifiedDuncan-Changmodelconsideringdistur-bance[J].JournalofZhejiangUniversity(EngineeringScience)，2012，46(1)：1-7.)

[8]KondnerRL，ZelaskoJS.Ahyperbolicstress-strainformulationforsands[C]//ProceedingsoftheSe-condPan-AmericanConferenceonSoilMechanicsandFoundationEngineering.Brasilia，Brazil，1963：289-324.

[9]DuncanJM，ChangCY.Nonlinearanalysisofstressandstraininsoils[J].JournaloftheSoilMechanicsandFoundationsDivision，1970，96(5)：1629-1653.

[10]JanbuN.Soilcompressibilityasdeterminedbyoedo-meterandtriaxialtests[C]//EuropeanConferenceonSoilMechanicsandFoundationsEngineering.Wiesbaden，Germany，1963：19-25.

(责任编辑：钟媛英文审校：尹淑英)

Influence of relative density on initial tangential modulus of gravelly sand

CHENChen1, 2

(1.SchoolofResources&CivilEngineering,NortheasternUniversity,Shenyang110819,China; 2.InfrastructureDivision,NortheastArchitecturalDesign&ResearchInstituteCo.Ltd.,Shenyang110003,China)

Inordertosolvetheproblemthatthestructuralchangeofsurroundingsoilduetothedisturbanceappearsduringtheconstructionprocessoffoundationpitandthenthechangeofthestrength-deformationcharacteristicsofsoilisinduced,thetypicalgravellysandwasselectedforthetriaxialconsolidationdrainedsheartestsunderdifferentconfiningpressures.TherelatedparametersfortheDuncan-Changmodelforthegravellysandwereobtained.TheinfluenceruleofinitialtangentialmodulusEiontherelativedensityDrforthegravellysandwasinvestigated.Inaddition,therelationshipbetweenDranddimensionlessparameterKwhichwererelatedtoEiwasfitted.TheresultsshowthattherelativedensityDrhasimportantinfluenceonthestrength-deformationcharacteristicsofgravellysand,andtherelationshipbetweenlnKandDrcanbedescribledbythequadraticfunction.

gravellysand;triaxialtest;relativedensity;Duncan-Changmodel;disturbedstate;initialtangentialmodulus;strength-deformationcharacteristic;logarithmicfitting

2016-01-05.

国家自然科学基金资助项目(51204029).

陈晨(1981-)，男，辽宁沈阳人，博士生，主要从事地下工程等方面的研究.

10.7688/j.issn.1000-1646.2016.05.18

TU411.4

A

1000-1646(2016)05-0579-05

*本文已于2016-09-07 16∶10在中国知网优先数字出版. 网络出版地址：http：∥www.cnki.net/kcms/detail/21.1189.T.20160907.1610.044.html