基于nested阵列的高分辨DOA估计*

刘鲁涛， 韩　丽， 张　明， 张　航

(哈尔滨工程大学 信息与通信工程学院， 哈尔滨 150001)



基于nested阵列的高分辨DOA估计*

刘鲁涛， 韩丽， 张明， 张航

(哈尔滨工程大学 信息与通信工程学院， 哈尔滨 150001)

针对nested阵列对邻近信号的分辨力受信噪比和快拍数等因素限制的问题，提出了基于nested阵列的加权子空间平滑MUSIC算法.该算法对协方差矩阵向量化以提高整个阵列的自由度，使用空间平滑恢复新接收数据矢量阵的秩，采用校正的噪声特征值对噪声子空间进行加权，并对信号子空间进行空间谱合成，得到新算法的空间谱函数.通过搜索空间谱函数极大值实现DOA估计.结果表明，该算法在低信噪比及小快拍数条件下，对间隔较近的信号具有高分辨力.

nested阵列； 协方差矩阵； 向量化； 自由度； 空间平滑； 加权； DOA估计； 高分辨力

波达方向(direction-of-arrival，DOA)估计是阵列信号处理领域的一个重要研究方向，被广泛应用于雷达、声源定位和通信等领域[1-3].子空间类算法[4-7]已经成为DOA估计中最常用和最经典的算法，尤其以多重信号分类[8-10](multiple signal classification，MUSIC)为典型代表的算法随着信噪比的提高可以突破瑞利限，但其缺点是自由度不高，估计目标数最多为N-1(N为阵元数目).为了提高阵列的自由度，文献[11]使用最小冗余阵列通过构建增强协方差矩阵来增加阵列的自由度，但在实际应用中，这种阵列的最优阵元位置受限于计算机建模以及迭代算法的复杂程度；文献[12]基于高阶累计量的DOA估计算法实现阵列扩展，增加虚拟阵元，但是其缺点是需要很大运算量来计算信号的高阶累积量，需要较多的快拍数才能准确地估计出目标信号参数，且不能用于处理高斯信号的DOA估计；文献[13]针对非平稳信号的特性提出了一种Khatrio-Rao子空间估计算法，实现了在阵元数少于信号源数目情况下对准平稳信号的DOA估计，但其测角精度不高，且也不适用于平稳信号；在此基础上，文献[14]利用Khatrio-Rao(KR)积的性质提出了一种新的阵列构造方式，即nested阵列，使得阵列的自由度大大增加，对于M个物理阵元的阵列可以获得O(M2)个自由度，并提出了相应的基于空间平滑多重信号分类(spatial smoothing MUSIC，SS MUSIC)的DOA估计方法.虽然nested阵列可以提高阵列的自由度，解决了在信源数多于物理阵元数情况下对平稳信号的DOA估计，但是其在低信噪比及小快拍数的条件下，并没有提高对邻近入射信号的分辨率.

本文将噪声子空间与信号特征值倒数加权的信号子空间相结合，得到加权子空间平滑MUSIC(weighted subspace of spatial smoothing，WSSS MUSIC)算法的谱函数，充分利用了信号的信息，降低了噪声的影响，提高了nested阵列邻近信号的分辨力.

1　数据模型和阵列结构模型

1.1数据模型

假设L个远场窄带信号入射到M个阵元的线阵上，信源入射角度分别为θ1，θ2，…，θL，入射信号彼此相互独立.噪声是高斯白噪声与信号相互独立，则阵列接收数据矢量形式为

X(t)=AS(t)+N(t)

(1)

式中：X(t)为阵列的M×1维阵列接收数据矢量；S(t)为空间信号的L×1维矢量；N(t)为M×1维的噪声矢量；A=[a(θ1)，a(θ2)，…，a(θL)]为M×L维的阵列流型，其中

a(θk)=[exp(-j2πd1sinθk/λ)，

exp(-j2πd2sinθk/λ)，…，

exp(-j2πdMsinθk/λ)]T

(2)

式中：di为第i个阵元相对阵列参考点的位置；λ为波长，则阵列接收数据的协方差矩阵为

(3)

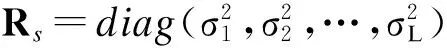
(4)

Khatri-Rao积的定义：用符号“⊙”表示Khatri-Rao(KR)积，两个矩阵A(N×K)和B(M×K)具有相同的列数，它们的KR积[13]为A⊙B=[a1⊗b1，a2⊗b2，…，aK⊗bK]=

(5)

式中：ak，bk分别为矩阵A和B的第k列；vec(·)为将矩阵的每一列元素排成一列，形成一个新的列向量.

KR积具有如下性质：

若A∈CN×K，B∈CM×K和D=diag(d)，且d∈CK×1，则

vec(ADBH)=(B*⊙A)d

(6)

式中，*为复共轭.

利用上述性质，且假设信号是相互独立的，则式(3)可化简为

z=vec(RXX)=

(7)

(8)

式中，

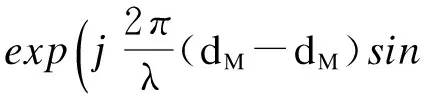
(i=1，2，…，M；j=1，2，…，M)

(9)

由式(9)可看出，此阵列流型类似于多输入多输出(multiple input multiple output，MIMO)雷达[15]，此阵列的阵元位置由集合{di-dj，1≤i，j≤M}(di，dj分别为第i个和第j个阵元的位置)中相异的值来决定，其相异值远大于物理阵元数M，因此增大了阵列的自由度.

1.2二阶nested阵列的阵列结构

在阵元数固定的前提下，为了使相异值最多(自由度最大)，文献[11]提出了一种基于KR积的阵列构造方式，称其为nested阵列.一个标准的二阶nested阵列是由两个相邻的均匀线阵(uniform linear arrays，ULA)串联构成的，内层的ULA有M1个阵元，阵元间距为d1，外层的ULA有M2个阵元，其阵元间距为d2=(M1+1)d1，则第1个ULA的阵元位置为S1={nd1，n=1，2，…，M1}，第2个ULA的阵元位置为S2={m(M1+1)d1，m=1，2，…，M2}，一个二阶nested阵列阵元总数为M=M1+M2，其结构示意图如图1所示.

图1　二阶nested阵列的结构示意图Fig.1　Schematic structure of second-order nested array

一个阵元总数为M的nested阵列，由KR积可产生(M2-2)/2+M个虚拟阵元，此虚拟阵列为阵元间距d1的ULA，其阵元位置集合为

S={ld1，l=-N，-(N-1)，…，N；

N=M2(M1+1)-1}

(10)

这样便增加了nested阵列的自由度，为实现信号源数目多于物理阵元总数的DOA估计提供了可能.

2　波达方向估计

上文对阵列接收数据协方差矩阵进行了向量化，使得到的新接收数据矢量z的秩变为1，并且由KR积产生的虚拟阵列为ULA，用类似空间平滑算法[16]恢复矩阵z的秩.首先，从构造的新阵列流型(A*⊙A)∈CM2×L中移除相同的行，然后对其排序，使第i行的元素对应于虚拟阵列的阵元位置为(-M2/4-M/2+i)d1，得到矩阵A1∈C((M2-2)/2+M)×L，这个操作类似移除矩阵z中相应的行，排序得到新的矩阵为

(11)

式中，e0∈C((M2-2)/2+M)×1，为除了第(M2/4+M/2)个元素是1，其余元素均为0的列向量.最后把矩阵z1分成(M2/4+M/2)个重叠的子阵，其中，每个子阵有(M2/4+M/2)个元素，第i个子阵的阵元位置为

(12)

第i个子阵对应的阵列接收数据矢量为

(13)

式中，矩阵A1i为(M2/4+M/2)×L维，其包含矩阵A1中从第(M2/4+M/2-i+1)行到第((M2-2)/2+M-i+1)行的元素.

由上面的分析容易得到

(14)

式中，

Φ=diag(exp(-jφ1)，exp(-jφ2)，…，exp(-jφL))

其中，φk=2πd1sinθk/λ.令

Ri

(15)

对Ri进行平均，可得到平滑后的新接收数据的协方差矩阵为

RSS

(16)

平滑后的ULA子阵阵元数MSS=M2/4+M/2，且平滑后的阵列流型为

ASS=[aSS(θ1)，aSS(θ2)，…，aSS(θL)]

(17)

式中，

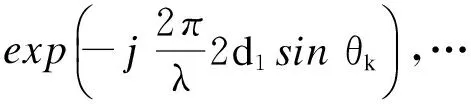
(18)

由此可看出，此阵列流型同有MSS个阵元的ULA阵列流型相同.于是可以构造如下SS MUSIC算法的空间谱函数

(19)

式中，EN为最小特征值对应的噪声子空间.

3　WSSS MUSIC算法

(20)

利用校正后的噪声特征值对噪声子空间进行加权处理，可以提高噪声特征值信息量的利用率，而且校正值μ不影响信号特征值，可以保证目标信号的波达方向估计稳定且准确.由式(20)可知，校正值μ的选取会对算法的估计性能产生很大的影响，若μ值选取的过小，会使得对噪声的抑制作用不明显；若μ值选取的过大，会使信号特征值与噪声特征值的差别太小，降低了目标信号波达方向估计的准确率，因此选择一个最优的校正值μ十分重要.从实际的大量实验数据可知，噪声特征值中的最大值与其最小值之比小于2，即

λL+1/λMSS<2

(21)

将式(20)代入式(21)可得

(22)

(23)

(24)

将式(24)代入式(19)中得到校正后的噪声子空间的谱函数为

(25)

在非理想环境下，通过校正值μ可以使噪声特征值的发散程度受到抑制，可以在一定程度上抑制噪声的影响，提高算法的分辨率.对噪声子空间进行加权也只是利用了噪声子空间的信息，却没有充分利用信号子空间的信息.由于特征分解协方差矩阵得到的信号子空间受噪声起伏的影响相对较小，对非理想环境下引起的误差不敏感，因此，为了充分利用新接收数据的信号子空间所包含的信息，可以利用主特征值的倒数对信号子空间进行加权，得到的谱函数表达式为

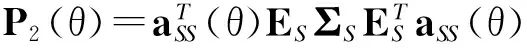
(26)

WSSS MUSIC算法不仅降低了噪声的影响，而且有效地利用了新接收数据信号子空间的信息，使得算法在低信噪比和少快拍数的非理想情况下，对邻近信号具有较高的分辨率，其空间谱函数为

(27)

算法的具体步骤如下：

1) 计算快拍数据协方差矩阵RXX，将其向量化，移除相同的行并排序，得到新的阵列接收数据矢量z；

2) 用空间平滑技术恢复矢量阵z的秩，并求得协方差矩阵RSS；

3) 对RSS进行特征值分解，将最大特征值对应的特征矢量构成的子空间定义为信号子空间ES=[v1，v2，…，vL]，最小特征值对应的特征矢量构成的子空间定义为噪声子空间EN=[vL+1，vL+2，…，vMSS]；

4) 根据式(27)求出WSSS MUSIC算法的空间谱函数进行谱峰搜索.

4　仿真实验

实验1考虑两个非相干的等强信号入射二阶nested阵列，入射方向分别是10°和12°，信噪比为2 dB，快拍数为200，本文算法和SS MUSIC算法的空间谱图比较如图2所示.

图2　两种算法的空间谱比较Fig.2　Comparison in spatial spectra of two algorithms

由图2可以看出，在低信噪比和小快拍数条件下，本文方法能够准确检测出两个非常邻近的信号(10°，12°)，而SS MUSIC算法的两个邻近信号的谱峰在空间谱上混叠成一个谱峰，算法失效.

实验2考虑两个非相干等强信号入射二阶nested阵列，入射角分别为θ1=10°，θ2=θ1+Δθ，其中，Δθ∈[1°，8°]，信噪比为0 dB，快拍数为200，本文方法和SS MUSIC算法的分辨概率随角度间隔变化的曲线如图3所示.

图3　分辨概率随角度间隔的变化曲线Fig.3　Change curves of resolution probability with angle interval

由图3可以看出，在低信噪比及小快拍数条件下，在角度间隔(小于5°)相同时，本文算法的分辨概率要比SS MUSIC算法高.而在识别成功率为1的前提下，本文算法有着更好的角度分辨率(角度间隔为4°).

实验3两个非相干等强信号源入射方向分别为10°和12°，在使用快拍数为200的条件下，设置信噪比从-4 dB按步长1 dB的间隔增加到10 dB时，进行1 000次Monte-Carlo实验.对本文算法、SS MUSIC算法以及12个阵元ULA的MUSIC算法成功分辨概率进行比较如图4所示.

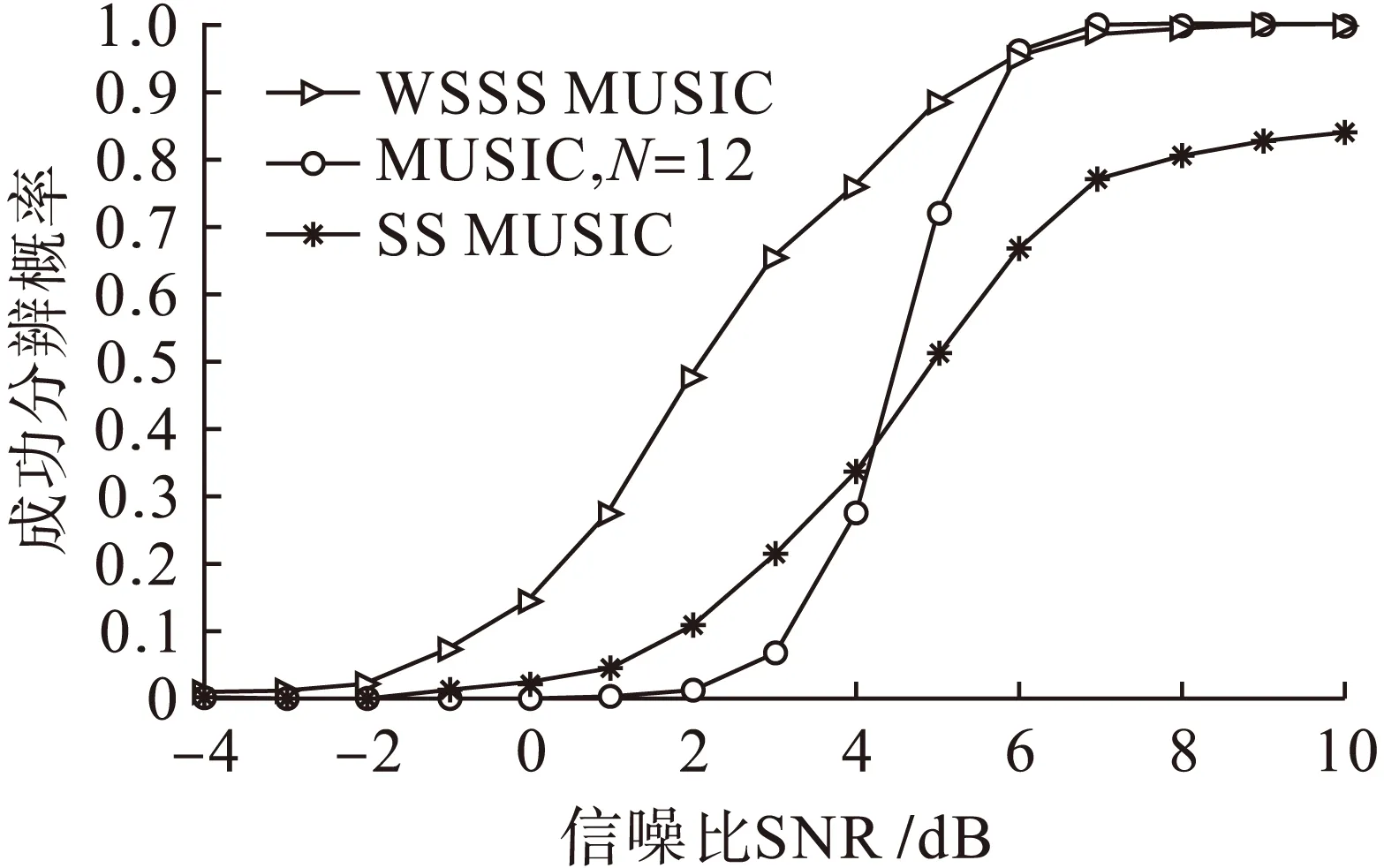
图4　三种算法成功分辨概率随信噪比的变化曲线Fig.4　Change curves of success resolution probability with SNR for three algorithms

由图4可以看出，在快拍数一定的条件下，随着信噪比的增加，三种算法邻近信号成功分辨率均随之增大.但在小信噪比的时候，本文算法相对两个邻近信号分辨的成功概率最高.而SS MUSIC算法由于受信噪比及快拍数的限制无法使两个邻近信号(10°和12°)的成功分辨概率达到1，进一步说明了本文算法的分辨性能.

实验4信源入射信号度不变，信噪比为5 dB，设置快拍数从1按步长40增加到601，进行1 000次Monte-Carlo实验.本文算法、SS MUSIC算法及12个阵元ULA的MUSIC算法邻近信号成功分辨概率随快拍数变化曲线如图5所示.

图5　三种算法成功分辨概率随快拍数的变化曲线Fig.5　Change curves of success resolution probability with number of snapshots for three algorithms

由图5可以看出，在信噪比一定的条件下，三种算法对邻近信号的成功分辨概率均随着快拍数的增加而增大.而在快拍数较少时，WSSS MUSIC算法对两个邻近信号的成功分辨概率明显优于其他两种算法，在快拍数较大时，WSSS MUSIC算法的成功分辨概率几乎和12个阵元ULA的MUSIC算法同时达到1.

5　结　论

本文提出了一种WSSS MUSIC算法，该方法通过对协方差矩阵向量化产生新接收数据，并将噪声特征值加权子空间与加权信号子空间相结合，充分利用新接收数据协方差的特征值信息.仿真结果表明，在低信噪比和小快拍数条件下，WSSS MUSIC算法对邻近信号的分辨性能优于SS MUSIC算法和具有相同物理孔径的12阵元ULA的MUSIC算法，在实际应用中节省了阵元数，降低了硬件成本.

[1]Hassanien A，Vorobyov S.Transmit energy focusing for DOA estimation in MIMO radar with collocated antennas [J].IEEE Transactions on Signal Processing，2011，59(6)：2669-2682.

[2]初萍，司伟建.基于延时相关预处理的MUSIC算法 [J].沈阳工业大学学报，2013，35(1)：93-98.

(CHU Ping，SI Wei-jian.MUSIC algorithm based on delay correlation preprocessing [J].Journal of Shen-yang University of Technology，2013，35(1)：93-98.)

[3]Mousavi P，Shafai L，Veidt B，et al.Feed-reflector design for large adaptive reflector antenna (LAR) [J].IEEE Transactions on Antennas and Propagation，2001，49(8)：1142-1154.

[4]Andersen J B.Array gain and capacity for known random channels with multiple element array at both ends [J].IEEE Journal on Selected Areas in Communications，2000，18(11)：2172-2178.

[5]王进，卢影，孙开伟，等.基于演化超网络的DNA微阵列数据分类方法 [J].重庆邮电大学学报(自然科学版)，2014，26(5)：679-685.

(WANG Jin，LU Ying，SUN Kai-wei，et al.DNA microarray data classification based on evolutionary hypernetworks [J].Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition)，2014，26(5)：679-685.)

[6]刁鸣，陈超，杨丽丽.四阶累积量阵列扩展的传播算子测向方法 [J].哈尔滨工程大学学报，2010，31(5)：652-656.

(DIAO Ming，CHEN Chao，YANG Li-li.Propagator method for direction of arrival estimation based on an array extension of the fourth-order cumulant [J].Journal of Harbin Engineering University，2010，31(5)：652-656.)

[7]Qian C，Huang L，So H C.Improved unitary root-MUSIC for DOA estimation based on pseudo-noise resampling [J].Signal Processing Letters，2014，21(2)：140-144.

[8]Grover R，Pados A，Medley M J.Subspace direction finding with an auxiliary vector basis [J].IEEE Transactions on Signal Processing，2007，55(2)：758-763.

[9]Birot G，Albera L，Chevalier P.Sequential high resolu-tion direction finding from higher order statistics [J].IEEE Transactions on Signal Processing，2010，58(8)：4144-4155.

[10]Feng G Y，Ming J，Liu S，et al.Real-valued MUSIC for efficient direction estimation with arbitrary array geometries [J].IEEE Transaction on Signal Processing，2014，62(6)：1548-1560.

[11]Gu J F，Zhu W P，Swamy M N S.Minimum redundancy linear sparse subarrays for direction of arrival estimation without ambiguity [C]//2011 IEEE International Symposium on Circuits and Systems (ISCAS).Rio de Janeiro，Brazil，2011：390-393.

[12]Cao S，Ye Z，Hu N，et al.DOA estimation based on fourth order cumulants in the presence of sensor gain-phase errors [J].Signal Processing，2013，93(9)：2581-2585.

[13]Ma W，Hsieh T，Chi C.DOA estimation of quasistationary signals with less sensors than sources and unknown spatial noise covariance：a Khatri-Rao subspace approch [J].IEEE Transaction on Signal Processing，2010，58(4)：2168-2180.

[14]Han K，Nehorai.An improved source number detection and direction estimation with nested arrays and ULAs using jackknifing [J].IEEE Transaction on Signal Processing，2013，61(23)：6118-6128.

[15]Xie R，Liu Z，Zhang Z J.DOA estimation for mono static MIMO radar using polynomial rooting [J].Signal Processing，2010，90(12)：3284-3288.

[16]Cai B，Li Y M，Wang H Y.Forward/backward spatial reconstruction method for directions of arrival estimation of uncorrelated and coherent signals [J].IET Microwaves，Antennas and Propagation，2012，13(6)：1498-1505.

(责任编辑：景勇英文审校：尹淑英)

DOA estimation with high resolution based on nested array

LIU Lu-tao, HAN Li, ZHANG Ming, ZHANG Hang

(College of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

In order to solve the problem that the resolution of nested array for adjacent signals is limited by such factors as signal to noise ratio (SNR) and number of snapshots, a weighted subspace smoothing MUSIC algorithm was proposed based on the nested array. The covariance matrix was vectorized in the algorithm to improve the degrees of freedom of whole array. The spatial smoothing was used to recovery the rank of newly received data vector matrix, and the corrected noise eigenvalues were adopted to weight the noise subspace. In addition, the spatial spectrum of signal subspace was synthesized, and the spatial spectrum function of new algorithm was obtained. Through searching the maximum value of spatial spectrum function, the DOA estimation was realized. The results show that under the condition of low SNR and small number of snapshots, the algorithm has high resolution of signals with relatively close interval.

nested array; covariance matrix; vectorization; degrees of freedom; spatial smoothing; weighting; DOA estimation; high resolution

2015-10-15.

国家自然科学基金资助项目(61202410).

刘鲁涛(1977-)，男，黑龙江哈尔滨人，副教授，博士，主要从事宽带信号处理、检测与识别等方面的研究.

10.7688/j.issn.1000-1646.2016.05.10

TN 911.6

A

1000-1646(2016)05-0531-06

*本文已于2016-05-12 13∶56在中国知网优先数字出版. 网络出版地址：http：∥www.cnki.net/kcms/detail/21.1189.T.20160512.1356.008.html