大型空间环型天线结构动力学分析*

范震 郭翔鹰 张伟

（北京工业大学机电学院，机械结构非线性振动与强度北京市重点实验室，北京 100124）

大型空间环型天线结构动力学分析*

范震 郭翔鹰 张伟

（北京工业大学机电学院，机械结构非线性振动与强度北京市重点实验室，北京 100124）

本文对大型空间环型天线结构振动的基本形式进行研究，选择边界条件为伸展臂与桁架结构连接面的固定约束.网格划分采用四面体单元与六面体单元结合的方法，杆件体结构规则采用六面体单元格，刚性连接处由于结构复杂采用四面体单元格.前四阶模态分析结果表明天线存在扭转振动、弯曲振动、横摇振动、呼吸振动等四种基本振动形式.研究了材料参数和边界条件的选取对振动模态和固有频率的影响.所得结果能为结构非线性动力学分析中模态函数选取和共振形式的分析提供重要参考.施加简谐激励研究大型空间环型天线稳态受迫振动响应，该结果对于预测结构的动力学特性以及避免共振具有重要的指导意义.

大型空间环型天线结构，扭转运动，模态分析，材料参数，谐响应

引言

随着航天技术的迅速发展，对于未来新型卫星天线的要求也在不断提高.大口径，高精度，低质量，高强度已经成为大型卫星天线设计的必然趋势，同时卫星天线又面临航天器运载空间及运载能力的限制.解决这一矛盾的关键技术在于天线结构型式的合理设计，使大型卫星天线能被现有的运载工具送入轨道，同时满足卫星多功能、大容积、长寿命等功能的需要.目前大型空间卫星普遍设计成可展结构，完成展开后锁定来保持工作状态［1-5］.为了国防技术以及国民经济的迫切需求，尤其是航空航天技术的发展需要，空间大型网架式可展天线的研制在许多国家都非常受重视，我国研究现状处于起步阶段，因此对大型环状天线振动特性进行研究对保证天线稳定工作具有重要意义［6-7］.

空间可展开桁架结构形式多样，并且具有收缩体积小、刚度高等特点，可展开桁架结构可作为桁架式索网抛物面天线反射器的周边支撑结构.无论是理论、试验研究方面还是实际应用方面，桁架式可展开天线都是国际宇航界较为关注的热点［8］. 1990年，Astro航空航天公司研制了周边环形析架可展开天线，该天线代表了目前可展开天线的技术水平.国内该天线研究现状处于起步阶段［9-18］.

本文利用FEM的方法对实际可展天线结构进行仿真，通过四面体六面体相结合的方式进行网格划分，并选取适当的边界条件，进行模态分析得到了天线结构的谐振频率和振型.研究边界条件和材料参数对结构振型和固有频率的影响.在非线性动力学建模过程中选取模态振型时，很难初步了解天线可能的振动形式，现在进行模态分析计算，对可能的振动形式进行分析，为以后非线性动力学建模过程中模态振型选择提供重要依据，对提高非线性动力学计算精度具有重要指导意义.同时研究结果为后续天线振动模态的选取以及参数共振的比例关系的研究提供重要参考［23］.

1 大型空间环型桁架结构建模

ANSYS软件是融合了结构、热、流体等于一体的通用有限元分析软件，其优点之一就是能够分析复杂多体结构.

在结构动力学中，系统的振动特性可以用模态来描述，表征模态的各阶参数是振动系统的各阶固有频率、固有振型等，建立用模态参数表示的振动系统的运动方程并确定其模态参数的过程就是模态分析［19-21］.用有限元法对网架式天线结构进行仿真共三个部分.第一部分是前处理，包括建模、选取单元类型、定义材料参数和划分网格.第二部分是求解模块，ANSYS中提供了强大的结构分析模块，可以用于结构的动态性能分析，包括模态分析.第三部分是后处理，通过后处理模块，得到模态分析［22］.

空间环形桁架是由n个结构完全相同的平行四边形单元组成，这些单元在相交处通过固定夹角的铰链相连接成为一个封闭的多边环型结构.其中平行四边形单元结构由竖杆、横杆、斜杆三种杆件组合而成.杆件为空心管状结构，杆件直径为20mm和18mm两种，杆件壁厚度均为1.5mm，空心杆件结构可以有效减轻天线整体的质量，从而提高天线机动性与安全性.由于环型桁架天线铰链连接处包含复杂结构，这种复杂结构对网格划分收敛性影响较大，本文将天线杆件间的铰链连接简化为与杆件壁厚相等的刚性连接，从而使得模型获得较好的收敛性.本文简化后的天线有限元结构模型如图1所示.

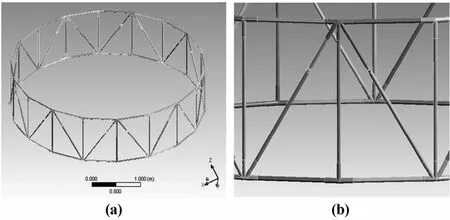
图1 大型环型桁架天线有限元模型Fig.1 The FEM model of the large deployable truss antenna

1.1 模型尺寸与材料参数

环型桁架天线的结构尺寸参数如表1所示.

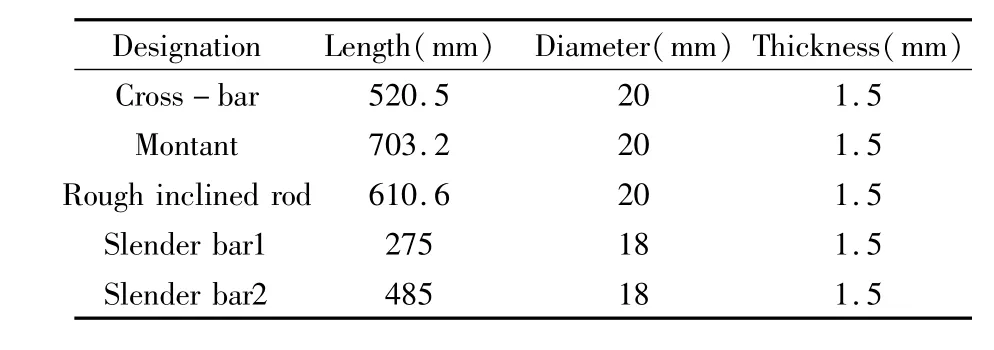
表1 天线整体尺寸参数Table 1 Dimension parameter of antenna

本文主要研究了结构尺寸与材料参数对环型桁架天线结构振动形态的影响，选取的材料为某种超强碳纤维缠绕，材料参数如表2所示.

表2 天线材料参数Table 2 Material parameter of antenna

1.2 边界条件的选取

环型桁架天线结构由各杆件通过三杆节点和五杆节点连接而成.选取桁架结构边界条件为同一竖杆两端一个三杆节点和一个五杆节点处的固定约束，如图1所示，A为三杆节点B为五杆节点，其他位置为自由约束条件.如图2所示.

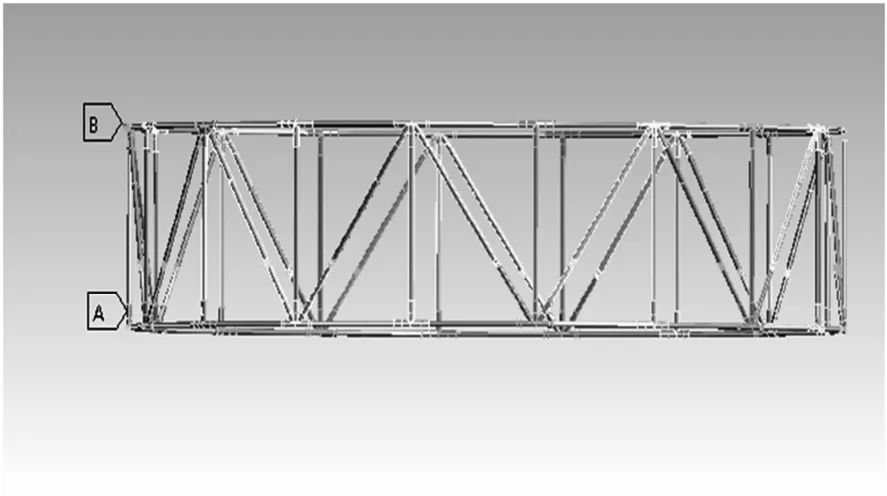
图2 大型环型桁架天线边界条件Fig.2 The boundary conditions of the large deployable truss antenna

1.3 网格的划分

网格常用的划分方式有四面体、六面体网格.其中四面体常应变单元具有简单，计算速度快，边界适应性强，易于自动划分且便于由表面向实体内部生成网格等特点.六面体单元由于变形特性好、计算精度高、相同精度要求所需网格单元数量较四面体少等诸多优点被广泛应用于三维有限元仿真等工程领域.

本文中环型桁架的杆件结构规则，为了提高精度采用六面体单元格.环型桁架结构刚性连接处由于结构复杂，需要采用边界适用性更强的四面体单元格.因此本文网格划分采用四面体单元与六面体单元结合的方法，兼顾两者优势.从划分过程中发现随着单元数目的增加，即单元尺寸的缩小，解的近似程度将不断改进，如果单元是满足收敛性要求的，其近似解最后将收敛于精确解.划分结果显示，共有212069个单元格.其划分情况如表3和图3所示.

表3 天线网格划分情况Table 3 Mesh status of antenna

图3 大型环型桁架天线网格划分Fig.3 Themeshing of the large deployable truss antenna

2 大型空间环型桁架结构仿真计算结果

模态分析模块主要分析结构的振动特性，利用模态分析得到大型空间环型天线结构振动的基本模式，计算结构前四阶振动频率和振动形式.并通过改变边界条件，研究不同边界条件对振动形式和振动频率的影响.

2.1 四种振动形式计算结果

采用1.2节边界条件.第一阶振型主要是刚体运动的弯曲变形.第二阶振型主要是整体的周向扭转振动形式.第三阶振型主要是径向呼吸振动形式.第四阶振型是横摇振动形式.

通过分析结果可以发现，振动的低阶模态主要以弯曲、扭转、呼吸运动为主.如图4所示，第一阶模态为整体的大范围弯曲运动，最大位移出现在固定约束的最远端，最大位移方向主要为轴向.如图5所示，第二阶模态为周向的大范围扭转运动，最大位移出现在固定约束的最远端，最大位移方向主要为周向.第三阶模态为径向的呼吸运动，最大位移出现在固定约束的最远端，最大位移方向主要为径向.第四阶模态为整体的横摇运动，最大位移出现在固定约束的两侧端，在整体横摇的同时，出现局部柔性变形.随着模态阶数和固有频率的升高，天线振动出现高阶柔性体变形.

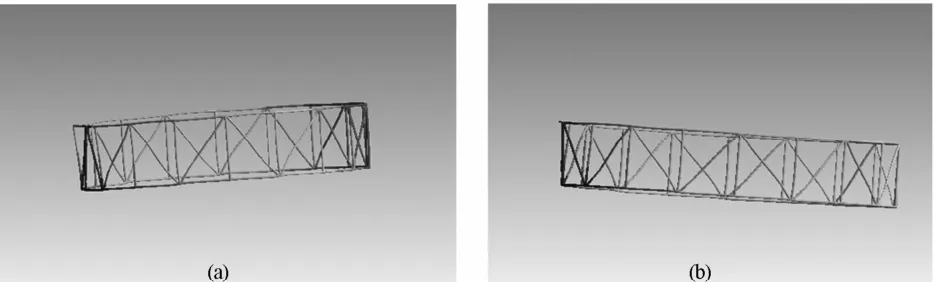
图4 大型环型桁架天线第一阶振型Fig.4 The firstmode shape of the large deployable truss antenna

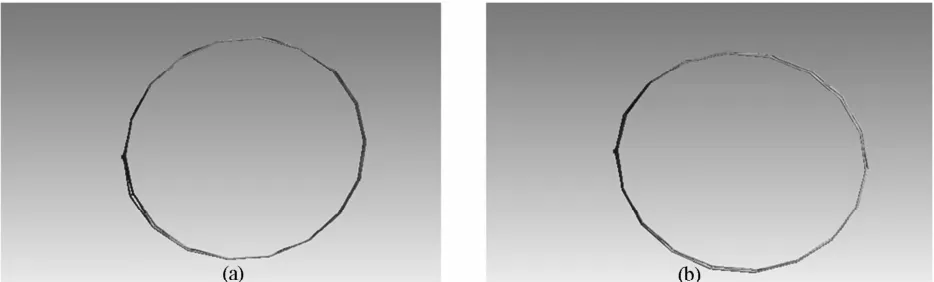
图5 大型环型桁架天线第二阶振型Fig.5 The second mode shape of the large deployable truss antenna

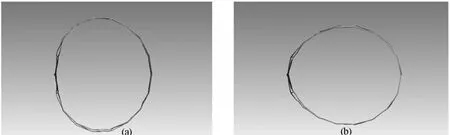
图6 大型环型桁架天线第三阶振型Fig.6 The third mode shape of the large deployable truss antenna

图7 大型环型桁架天线第四阶振型Fig.7 The fourth mode shape of the large deployable truss antenna

2.2 四种振动频率计算结果

天线的各阶模态对应的频率分析结果如表4所示.

表4 天线前4阶固有频率Table 4 First four order frequency of antenna

由频率分析可以看出，前三阶振动的频率低且频率接近，天线振动可能存在几种振动形式的运动耦合的情况，可以进一步研究几种振动形式耦合的复杂非线性运动.

2.3 呼吸振动形式计算结果

改变边界条件，在1.2节设置边界条件的基础上，增加竖杆在天线结构轴向的约束，计算天线前六阶振动形式和振动频率.结果显示，前六阶呼吸运动为具有振动峰值个数与振动阶数相同的呼吸运动，如图8～13所示.

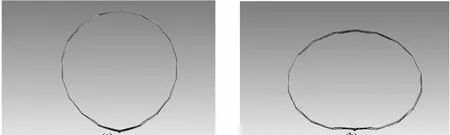
图8 大型环型桁架天线呼吸第一阶振型Fig.8 The first breathingmode shape of the large deployable truss antenna

图9 大型环型桁架天线呼吸第二阶振型Fig.9 The second breathingmode shape of the large deployable truss antenna

图10 大型环型桁架天线呼吸第三阶振型Fig.10 The third breathingmode shape of the large deployable truss antenna

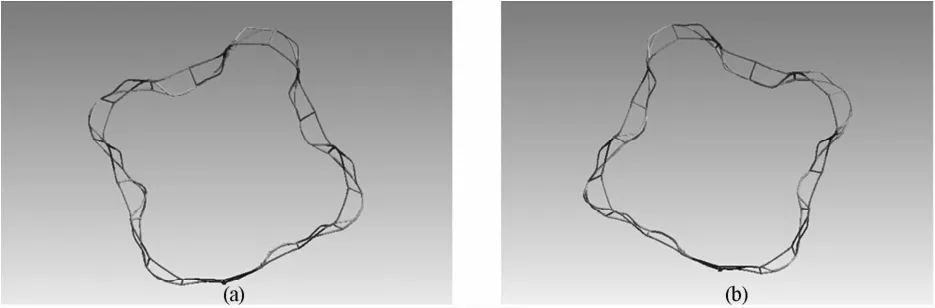
图11 大型环型桁架天线呼吸第四阶振型Fig.11 The fourth breathingmode shape of the large deployable truss antenna

可见边界条件不同，结构发生振动形式不同.在此种边界条件下，振动均为径向的呼吸运动.振动最大峰值点出现规律变化.一阶呼吸运动共有一个振动峰值点，位置在距离固定边界条件处周向180度处.随着阶数增加振动峰值点个数也增加，n阶呼吸运动共有n个振动峰值点，且振动峰值点周向均匀分布.

图12 大型环型桁架天线呼吸第五阶振型Fig.12 The fifth breathingmode shape of the large deployable truss antenna

图13 大型环型桁架天线呼吸第六阶振型Fig.13 The sixth breathingmode shape of the large deployable truss antenna

2.4 呼吸振动形式频率计算结果

天线的呼吸振动形式的前6阶模态对应的频率分析结果如表5所示.

表5 天线前6阶固有频率Table 5 The first six order frequency of antenna

由频率分析可以看出，前二阶振动的频率低且频率接近.此种边界条件的前四阶振动频率分别为：1.8668Hz，1.9712Hz，3.5555Hz，4.9482Hz.1.2节所设置边界条件下前四阶振动频率为：1.7301Hz，1.8520Hz，1.9855Hz，3.2223Hz.可见，改变天线边界条件增加竖杆在天线结构轴向的约束，使得相同阶数振动形式的固有频率升高.因此为提高计算精度，应当重视对边界条件的合理选择.

3 材料参数对振动频率的影响分析

天线发射过程中，需要考虑发射卫星天线的质量，因此会采用较小密度，减轻重量.本文采用的材料是强度大的碳纤维材料，为了分析采用高强度材料对固有频率的影响，下面针对普通工程钢材料的天线进行动力学分析，所采用工程钢参数如表6所示，频率计算结果如表7所示.同时为了研究不同弹性模量对前4阶固有频率的影响，计算了不同强度碳纤维材料天线的固有频率.

表6 天线采用工程钢的材料参数Table 6 Material parameters of antenna steel

表7 线不同材料参数的前4阶固有频率Table 7 The first four order frequency of the antenna with differentmaterial

表7中，不同弹性模量的碳纤维材料最低阶固有频率分别为1.7301Hz，1.8207Hz，1.9016Hz明显高于传统工程钢材料的固有频率1.3204Hz.不同弹性模量的碳纤维材料，随着材料弹性模量的增加天线各阶固有频率缓慢增加.应当选择合适的弹性模量的碳纤维材料.高强度材料使得天线低阶振动频率明显增高，需考虑结构阻尼对降低固有频率的影响，使振动频率保持在合理范围，保证天线工作精度.

4 大型空间环型天线结构谐响应分析

采用基于模态叠加法的谐响应分析，分析大型空间环型桁架结构的稳态受迫振动.施加随时间变化的简谐外激励作用点在周向距离固定边界条件180度处的竖杆下端点.余弦形式外激励力为：F =F0cos（Ωt），其中F0=100N.

图14 大型环型桁架天线激励作用点与观测点Fig.14 The loading point and observation point of the large deployable truss antenna

图15中可以看到，设置扫频范围为0～4Hz时，在频率为1.7Hz时，在观测点A的出现应力最大值为1.7Mpa，另提取1.7Hz时的整体天线结构整体的应力云图，如图16所示，天线的最大应力位于施加固定边界条件的竖杆件右侧第一根竖杆的上端点上，大小为162.36 Mpa.

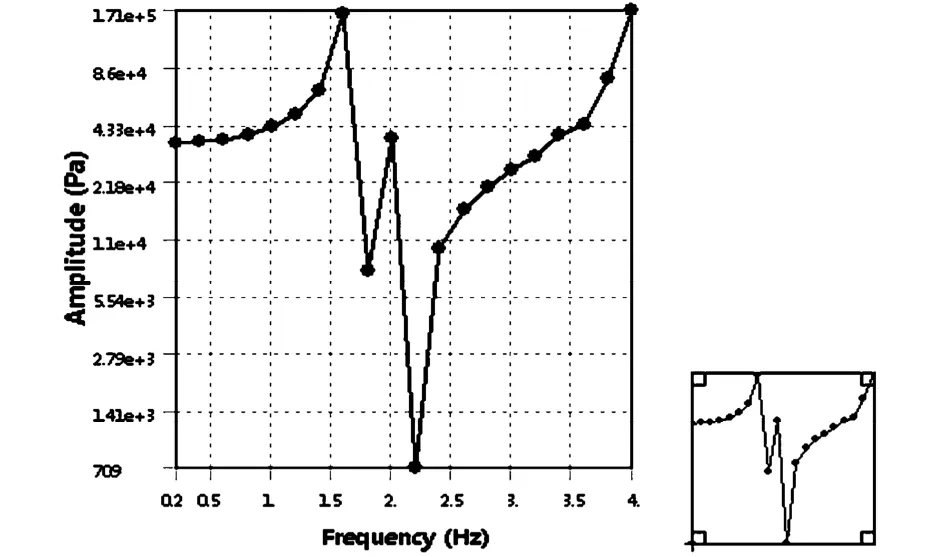
图15 0～4Hz频率范围观测点应力-频率曲线Fig.15 The stress-frequency curve of the observation point in the frequency range of 0-4Hz

图16 1.7Hz频率的应力云图Fig.16 The stress contour of the antenna at the frequency of 1.7Hz

图17中可以看到，设置扫频范围为0～4Hz时，在频率为1.7Hz时，在观测点A的出现位移最大值为7.37cm，另提取1.7Hz时天线结构整体的位移云图，如图18所示，天线的最大位移位于周向距离固定边界条件180度处的竖杆下端点处.

图17 0～4Hz频率范围观测点位移-频率曲线Fig.17 The displacement-frequency curve of the observation point in the frequency range of 0～4Hz

图18 1.7Hz频率的为位移云图Fig.18 The displacement contour of the antenna at the frequency of 1.7Hz

在谐响应分析结果可以看到，应力响应的峰值与固有频率相对应.该结果对于预测结构的持续性动力特性和避免共振产生具有重要指导意义.

5 小结

模态分析与频率计算结果表明，大型环型桁架天线结构的低阶振动模态多以扭转运动与呼吸运动为主，这两种振动属于低频振动，振动形式集中产生的高能量对振动响应的影响大.故后续研究应以环形天线的低阶扭转振动与呼吸振动为主要研究对象.结构有限元计算结果能否更精确反应结构在实际振动形式和频率，除材料参数的选取外，还在于边界条件的确定合理与否.同时大型环型桁架天线结构的模态分析与频率计算为结构非线性动力学分析中模态函数选取和共振形式的分析都能提供重要参考，谐响应分析对于避免共振产生具有重要指导意义.

1 胡海岩，田强，张伟等.大型网架式可展开空间结构的非线性动力学与控制.力学进展，2013，43（4）：390～414 （Hu H Y，Tian Q，et al.Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes.Advances in Mechanics，2013，43（4）：390～414（in Chinese））

2 Nayfeh A H，Hefzy M S.Effective constitutive relations for large repetitive frame-like structures.International Journal of Solids and Structures，1982，18（11）：975～987

3 Burgardt B，Cartraud P.Continuum modeling of beam like lattice trusses using averagingmethods.Computers&structures，1999，73（1）：267～279

4 Stephen N G，Zhang Y.Coupled tension-torsion vibration of repetitive beam-like structures.Journal of Sound and Vibration，2006，293（1）：253～265

6 闵桂荣.卫星热控制技术.北京：宇航出版社，1991 （Min G R.The Satellite thermal control technology.Beijing：Aerospace Press，1991（in Chinese））

7 闵桂荣，郭舜.航天器热控制.北京：科学出版社，1998 （Min G R，Guo S.Spacecraft thermal control.Beijing：Science Press，1998（in Chinese））

8 安翔，冯刚，张铎.大型空间析架结构热分析的有限元方法.强度与环境，2000（2）：18～23（An X，Feng G，Zhang D.Finite-elementmode for the thermal analysis of largemain truss of space station′solar-array.Structure& Environment Engineering，2000（2）：18～23（in Chinese））

9 Tibert G.Deployable tensegrity structures for space applications［PhD Thesis］.Royal Institute of Technology，2002

10 Thomson M W.The AstroMesh deployable reflector.IUTAM-IASS Symposium on Deployable Structures：Theory and Applications.Springer Netherlands，2000：435～446

11 Thomson M W.The Astromesh deployable reflector.Antennas and Propagation Society International Symposium，IEEE，1999，3：1516～1519

12 Thomson M W.AstroMesh deployable reflectors for Kuand Ka-band commercial satellites.In：20th AIAA International Communication Satellite Systems Conference and Exhibit，2002：12～15

13 刘明治，高桂芳.空间可展开天线结构研究进展.宇航学报，2003，24（1）：82～87（Liu M Z，Gao G F.Advances in the study on structure for space deployable antenna.Journal of Astronautics，2003，24（1）：82～87（in Chinese））

14 Liu X N，Huang G L，Hu G K.Chiral effect in plane isotropic micropolar elasticity and its application to chiral lattices.Journal of the Mechanics and Physics of Solids，2012，60（11）：1907～1921

15 Luo GW，Zhang Y L，Xie JH.1：3 resonance bifurcation of a three-degree-of-freedom vibratory system with symmetrical rigid stops.Physics Letters A，2008，372（12）：2026～2031

16 Mahapatra D R.Equivalent constitutive model-based de-sign ofwave-absorbingmaterial system and controller.Journal of sound and vibration，2006，289（3）：509～528

17 张伟，胡海岩.非线性动力学理论与应用的新进展.北京：科学出版社，2009（Zhang W，Hu H Y.Advances in theory and application of nonlinear dynamics.Beijing：Science Press，2009（in Chinese））

18 赵孟良，关富玲.考虑摩擦的周边桁架式可展天线展开动力学分析.空间科学学报，2006（26）：220～227（Zhao M N，Guan F L.Deployment dynamic analysis of circular truss deployable antenna with friction.Chinese Journal of Space Science，2006（26）：220～227（in Chinese））

19 陈国荣.有限单元法原理及应用.北京：科学出版社，2009：1～3（Chen G R.The principle and application of finite elementmethod.Bejing：Science Press，2009：1～3 （in Chinese））

20 王助成，邵敏.有限单元法基本原理和数值方法.北京：清华大学出版社，1997：443～81（Wang Z C，Shao M. The principle and numericalmethod of finite elementmethod.Beijing：Tsinghua University Press 1997：443～81（in Chinese））

21 应隆安，陈传森.有限元理论与方法.北京：科学出版社，2009：688～700（Ying L A，Chen CS.The finite element theory and method.Beijing：Science Press，2009：688～700（in Chinese））

22 张洪信，吴俊飞，沈孝芹.有限元基础理论与ANSYS应用.北京：机械工业出版社，2006：1～3（Zhang H X，Wu JF，Shen X Q.The finite element theory and application of ANSYS.Beijing：Machinery Industry Press，2006：1～3 （in Chinese））

23 胡海良，张伟.两自由度非线性系统1：3内共振的渐进摄动分析.动力学与控制学报，2015，13：97～100（Hu H L，Zhang W.Two degree of freedom nonlinear system asymptotically 1：3 internal resonance perturbation analysis. Journal of Dynamics and Control，2015，13：97～100（in Chinese））

DYNAM ICS ANALYSISOF LARGE DEPLOYABLE MESH ANTENNA STRUCTURE*

Fan Zhen Guo Xiangying ZhangWei

（Beijing Key Laboratory of Nonlinear Vibrations and Strength of Mechanical Structures，College of Mechanical Engineering，Beijing University of Technology，Beijing 100124，China）

This paper focuses on the fundamental vibration mode of the large deployable antenna structure. Here，the boundary conditions are considered as fixed Supportaccording to the actual contact surface between the extended arm and truss.The gridmesh for the large deployable antenna structure is combined by both tetrahedral element and hexahedral element，where the hexahedral element is employed in the rod parts of the large deployable antenna structure，while tetrahedral element is in the joint parts of the large deployable antenna structure.The analysis results of the first four ordermodels show that the four basic vibration forms of the antenna contain the twistmotion，the bending motion，the roll motion and the breathing motion.These four vibration modes are important for the responses of the large deployable antenna，since they have the similar frequencies.It also analyzes the influence ofmaterial parameters and boundary conditions on themode shape and frequencies. The results also provide the important reference to the selection of modal function and the nonlinear dynamic analysis of resonance parameters for the large deployable antenna.The study of the forced vibration through the harmonic response analysis is alsomeaningful to predict the dynamic behaviour and avoid resonance.

large deployable mesh antenna structure，twisting motion，modal analysis，material parameters，harmonic response analysis Received 17 April 2015，revised 17 May 2015.

E-mail：sandyzhang0@yahoo.com

10.6052/1672-6553-2015-038

*The project supported by the National Natural Science Foundation of China（11202009，11290152）

2015-04-17收到第1稿，2015-05-17收到修改稿.

*国家自然科学基金资助项目（11202009，11290152）

E-mail：eagle2008guo@yeah.net